강화학습기초(4) - Temporal Difference Learning, SARSA

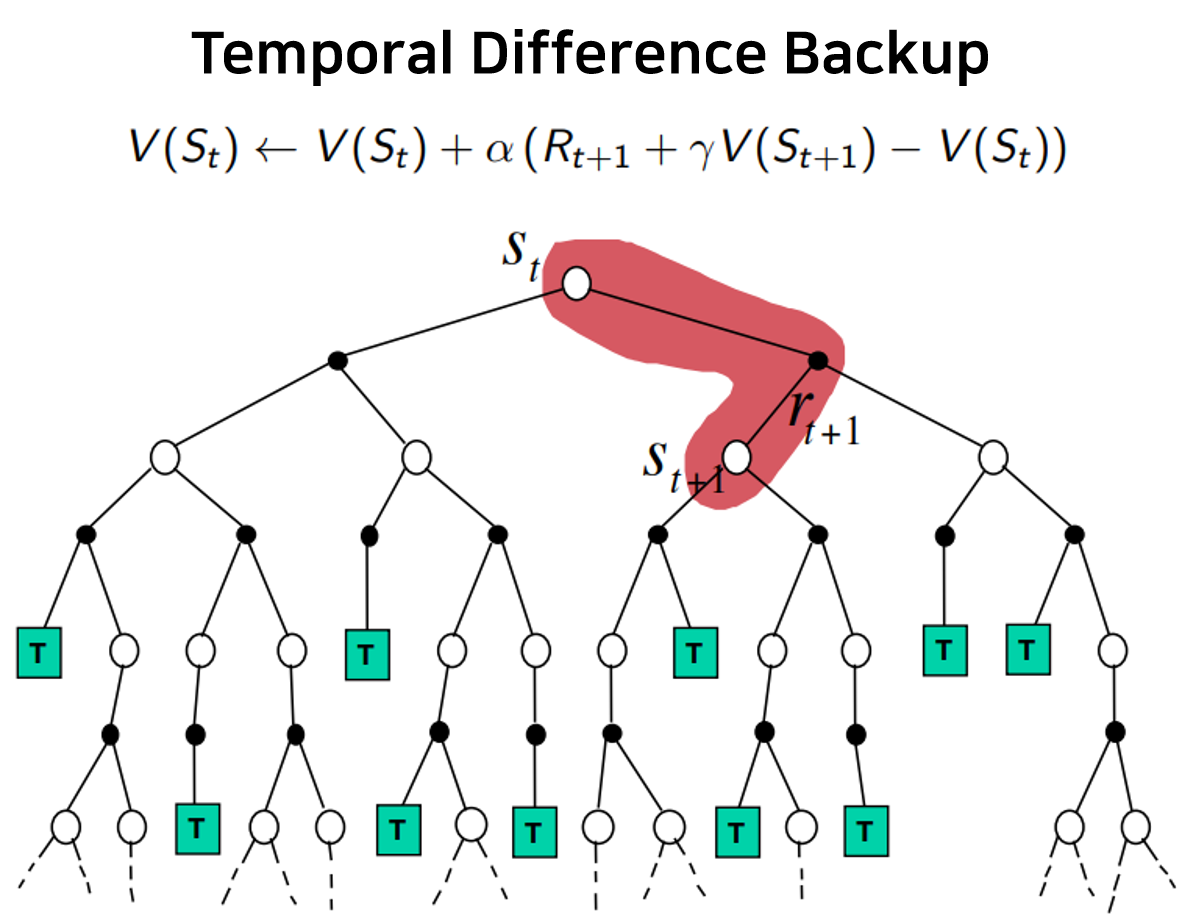
본 글에서는 두 번째 learning 방식인 temporal difference learning (TD)에 대해서 알아보도록 한다.

앞서 살펴본 MC는 episode가 종료되기 전까지 prediction이 진행되지 않는다는 단점이 있었다. 이에, MC처럼 sample backup을 하되 DP와 같이 time-step마다 prediction할 수 있는 방식이 바로 temporal difference learning이다.

Temporal Difference Learning

앞선 MC에서의 prediction은 아래와 같이 episode에서 실제로 얻어진 return $G_t$를 통해 이루어졌다.

한편 TD(0)에서는, 아래처럼 estimated return $R_{t+1}+\gamma V(S_{t+1})$을 통해 predict한다. (괄호 안 숫자 0의 의미는 후술하도록 하겠다.)

이 때, $R_{t+1}+\gamma V(S_{t+1})$를 TD target, $R_{t+1}+\gamma V(S_{t+1})-V(S_t)$를 TD error라고 칭한다.

따라서 MC와 같이 zero-initialized value function과 random policy로 시작하되, 매 time-step마다 sampling된 immediate reward와 다음 state의 value function으로 TD target을 구성하여 prediction을 진행하면 된다. 이는 bootstrapping(복원추출을 통해 true value를 estimate)을 진행하는 DP와 sampling을 통해 model-free하게 학습하는 MC의 특징을 모두 포함하고 있음을 알 수 있다.

이러한 TD는 매 time-step마다 prediction이 이뤄지므로 noise가 적어 학습의 variance가 낮지만 value function을 immediate reward만으로 bootstrapping하여 추정하므로 bias가 높다는 단점이 있다.

Learning Method	Bias	Variance
MC	실제 return 값을 이용하므로 낮음	Episode의 randomness에 의해 높음
TD	Immediate reward 값만으로 추정하여 높음	단일 step update의 적은 noise로 낮음

SARSA

이미 눈치챘을 수도 있지만 위 TD(0)의 prediction 관계식은 state-value function을 사용하므로 아직 model-free하지 않다. 따라서 매 time-step마다 아래와 같이 Q-value function에 대한 estimation이 이뤄져야 한다.

또한 local optimum에 빠지지 않도록 하기 위해 앞선 MC에서와 같이 $\epsilon$-greedy policy control도 적용할 수 있다. 이를 통해 만들어진 학습 방식을 SARSA라고 칭하며, 이는 매 time-step의 prediction에 필요한 $<S, A, R, S', A'>$로부터 지어진 직관적인 이름이다.

n-step TD

앞서 말했듯, TD는 오직 immediate reward 값만으로 value function을 업데이트하므로 높은 bias를 가진다. 이를 완화하며 MC와 TD의 장점을 모두 살리기 위해, 아래와 같이 agent가 위치한 state로부터 n-step이 지난 후 얻게 되는 n-step return $G_t^{(n)}$을 활용하는 방법이 있으며, 이를 n-step TD라고 칭한다.

이 때, n을 충분히 크게 하여 최종 state에 도달할 경우, MC와 동일해짐을 알 수 있다.

Forward-View of TD($\lambda$)

또한 $n$과 $\alpha$의 값에 따라 optimal policy와의 error 분포가 달라지게 되는데, 아래와 같이 각 $n$-step return $G_t^{(n)}$의 geometrically weighted sum $G_t^\lambda$를 TD target으로 설정하면 다양한 $n$-step TD의 장점을 적절히 취할 수 있으며, 이를 $\lambda$-return이라고 칭한다. (episode가 진행되는 정방향으로 update가 이뤄지므로 forward-view라는 명칭이 붙는다.)

하지만, 이는 MC에서와 같이 최종 state로부터 얻은 return까지 필요하므로 episode가 끝나야만 update를 할 수 있다는 문제점을 다시 불러일으킨다.

Backward-View of TD($\lambda$)

앞선 문제는 eligibility trace 개념을 적용하여 해결할 수 있다. 이를 쉽게 이해하기 위해 credit assignment problem을 생각해볼 수 있는데, 예컨대 'Bell'$\rarr$'Bell'$\rarr$'Bell'$\rarr$'Light'$\rarr$'Shock'의 순으로 발생한 사건(state)에 대해, "'Shock'의 발생은 'Bell'과 'Light' 중 어느 것으로부터 더 크게 기인했는가?" 라는 질문이 그에 해당한다.

위 질문에 대한 답은 아래의 두 heuristic으로 생각해볼 수 있다.

• Frequency heuristic : Most frequent state에 credit을 부여해, 'Bell'로부터 기인했다고 보는 것이다.
• Recency heuristic : Most recent state에 credit을 부여해, 'Light'로부터 기인했다고 보는 것이다.

여기서 credit이란, 결과(reward)에 대해 과거 상황(state)들이 영향을 미친 정도로 이해될 수 있다. 위의 두 heuristic을 모두 고려한 eligibility trace $E_t(s)$는 아래와 같이 정의되며, 이를 통해 episode 진행 중 방문한 모든 state에 대하여 value prediction을 수행할 수 있다. (Episode가 진행되는 역방향에 대해 TD error 값을 분배하므로 backward-view의 명칭이 붙는다.)

이는 time-step $t$에서 sampling된 $R_{t+1}$을 이전에 방문한 state들에게 적절한 가중치를 달아 배분하는 것으로 이해해볼 수 있다. 1)Recency heuristic은 time-step이 진행될수록 1보다 작은 값($\gamma\lambda$)으로 weighted되어 방문한지 오래된 state일수록 더 적게 반영해주는 방식으로 고려된다. 2)Frequency heuristic은 각 state에 방문할 때마다 $E_t(s)$ 값에 1을 더해주는 방식으로 고려된다. 따라서, state $s$의 $E_t(s)$ 값은 agent가 $s$에 방문하면 높아졌다가 점차 낮아지고, 다시 방문하면 높아졌다 낮아지는 형태로 값이 변하며, 해당 $s$의 $V(s)$ 값도 그에 비례하여 매 시간마다 update된다.

n-step SARSA / SARSA($\lambda$)

앞선 SARSA와 동일하게, n-step TD와 TD($\lambda$)의 state-value function을 Q-value function으로 바꾸어 model-free learning이 가능해지도록 하면 아래와 같아진다.

n-step SARSA    $\cdot\cdot\cdot$ single-step update의 high-bias 문제를 해결
$q_t^{(n)}=R_{t+1}+\gamma R_{t+2}+\cdot\cdot\cdot+\gamma^{n-1}R_{t+n}+\gamma^nQ(S_{t+n})$
$Q(S_t, A_t)\larr Q(S_t, A_t)+\alpha(q_t^{(n)}-Q(S_t, A_t))$

Forward-view SARSA($\lambda$)    $\cdot\cdot\cdot$ 각 n-step SARSA의 장점을 종합
$q_t^\lambda=(1-\lambda)\sum_{n=1}^\infin\lambda^{n-1}q_t^{(n)}$
$Q(S_t, A_t)\larr Q(S_t, A_t)+\alpha(q_t^\lambda-Q(S_t, A_t))$

Backward-view SARSA($\lambda$)    $\cdot\cdot\cdot$ episode가 끝나지 않아도 update할 수 있도록 개선
$E_0(s,a)=0$
$E_t(s,a)=\gamma\lambda E_{t-1}(s,a)[\text{ }+1, \text{ }\text{ } \text{if } s=S_t, \text{ }a=A_t\text{ }]$
$\delta_t=R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t)$
$Q(s,a) \larr Q(s,a)+\alpha\delta_tE_t(s,a)$

하지만 MC와 SARSA의 공통된 문제점은, 최종적으로 얻어내려는 target policy를 prediction 과정에서 다음 state를 선택하는 behavior policy로 그대로 활용하는 on-policy control에 해당하므로 local optimum에 빠지기 쉽다는 것이다. 이에, 다음 글에서는 학습과정의 episode를 결정하는 behavior policy와 얻어내려는 target policy를 서로 분리하여 해당 문제를 해결한 off-policy control 기법에 대해 다뤄보도록 하겠다.

---

References

• UCL Course on RL, David Silver
• Reinforcement Learning: An Introduction, Richard S. Sutton
• Fundamental of Reinforcement Learning, 이웅원