강화학습기초(5) - Off-Policy Control, Importance Sampling, Q-Learning

구명규·2023년 2월 9일

RL Basic

목록 보기

5/8

본 글에서는 세 번째 learning 방식인 off-policy control (Q-learning)에 대해서 알아보도록 한다.

앞서 살펴본 MC와 TD (SARSA)의 경우, prediction 과정에서 agent의 behavior을 target policy로 sampling하기 때문에 충분한 exploration이 이뤄지지 않아 local optimum에 쉽게 빠지게 되고, $\epsilon$ -greedy control를 진행할 경우 target policy에 불필요한 randomness가 부여된다는 단점이 있었다.

이에, behavior policy와 target policy를 이원화하여 exploration을 수행하면서도 optimal policy를 적절히 학습할 수 있도록 하는 방식이 off-policy control이다.

Importance Sampling

Off-policy의 핵심은 behavior policy $\mu(a|s)$ 를 통해 target policy $\pi(a|s)$ 를 추정한다는 것이다. 이는 현 target policy에 의한 optimal action이 있어도 다른 non-optimal action을 취하여 더 높은 return의 가능성을 탐색하려는 목적을 담고 있다. 하지만 " $\mu(a|s)$ 로 predict한 value function 값에 $\mu$ 와 다른 policy $\pi$ 의 규칙을 적용하여도 optimal policy $\pi^*$ 에 수렴하는가"란 의문이 생긴다.

이러한 학습방법이 유효한 근거는 바로 통계학의 importance sampling이란 개념으로부터 나온다. 이에 관해 간단히 살펴보자.

Distribution $P$ 를 따르는 random variable $X$ 에 대해, $f(X)$ 의 기댓값, $E_{X\sim P}[f(X)]$ 을 sampling하여 구한다고 가정해보자. 하지만 만약 함수 $f$ 에서 유효한 값을 가지는 정의역의 범위가 distribution $P$ 에서는 드물게 sampling된다면 해당 기댓값을 구하는데 어려움이 생길 것이다. 이를 해결하기 위해, 함수 $f$ 의 important region에서 쉽게 sampling되는 distribution $Q$ 로 $X$ 를 대신 sampling하여 기댓값 $E_{X\sim Q}[f(X)]$ 를 구한 뒤, 원래 구하려던 값으로 adjust하는 기법이 importance sampling이다.

이를 수식으로 나타내면 아래와 같다.

E_{X\sim P}[f(X)]=\sum P(X)f(X)\\ \text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ } =\sum Q(X)\frac{P(X)}{Q(X)}f(X)\\ \text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ } =E_{X\sim Q}[\frac{P(X)}{Q(X)}f(X)]

이 때, $P$ 를 nominal distribution, $Q$ 를 importance distribution, $\frac{P(X)}{Q(X)}$ 를 likelihood ratio (importance weight)라 칭한다. Likelihood ratio를 적절히 곱해주면 다른 distribution $Q$ 에서 얻은 sample로도 $P$ 에 대한 기댓값을 간접적으로 얻어낼 수 있는 것이다.

이러한 importance sampling 개념을 강화학습에 적용해보면, P는 구하려는 optimal policy, Q는 behavior policy, f는 value function에 대입해볼 수 있다.

Importance sampling for off-policy MC

우선 MC에 위 importance sampling을 적용해보자. Behavior policy $\mu$ 로 구한 return $G_t$ 에 전체 episode에 대한 likelihood ratio를 아래와 같이 곱해주면 target policy에 대한 corrected return $G_t^{\pi/\mu}$ 를 구할 수 있다. 여기서 likelihood ratio를 곱해주는 것은 쉽게 말해 behavior policy $\mu$ 에서 선택된 action과 target policy $\pi$ 을 사용하였을 때 선택되었을 action 간 차이를 보정하는 의미를 가진다.

G_t^{\pi/\mu}=\frac{\pi(A_t|S_t)}{\mu(A_t|S_t)}\frac{\pi(A_{t+1}|S_{t+1})}{\mu(A_{t+1}|S_{t+1})}\cdot\cdot\cdot\frac{\pi(A_T|S_T)}{\mu(A_T|S_T)}G_t

V(S_t)\larr V(S_t)+\alpha(G_t^{\pi/\mu}-V(S_t))

하지만 이는 $\pi$ 가 0이 아닌 값을 가질 때 $\mu$ 가 0의 값을 가지는 경우 발산하여 사용할 수 없으며, 각 time-step에서 $\pi$ 와 $\mu$ 값의 차이가 누적될수록 학습의 variance가 크게 증가한다는 단점이 있다.

Importance sampling for off-policy TD

이번엔 TD의 차례다. TD는 매 time-step마다 prediction이 이뤄지므로 아래와 같이 sampling correction을 한 번만 해주면 된다. $R_{t+1}+\gamma V(S_{t+1})$ 은 behavior policy $\mu$ 를 기반으로 구해진 값이다.

V(S_t) \larr V(S_t)+\alpha(\frac{\pi(A_t|S_t)}{\mu(A_t|S_t)}(R_{t+1}+\gamma V(S_{t+1}))-V(S_t))

이는 MC importance sampling에 비해 variance를 크게 감소시키지만 여전히 on-policy TD에 비해서는 높은 variance를 보인다.

Q-Learning

앞서 살펴본 importance sampling의 가장 큰 문제점은 학습의 속도 저하를 일으키는 높은 variance이다. 여기서 만약, agent의 action은 behavior policy를 기반으로 선택하되, value function에 대한 prediction을 수행할 때는 target policy를 사용한다면 importance sampling을 할 필요가 없어진다. 이를 활용해 off-policy 학습의 variance를 다시금 줄이는 방식이 아래의 Q-learning이다.

Q-Learning
1. Model-free policy control을 위해 Q-value function을 사용
2. 현재 state $S_t$ 에서의 action $A_t$ 는 behavior policy $\mu(\cdot|S_t)$ 를 따라서 선택
3. Action-value function을 사용하기 위해 선택하는 다음 state $S_{t+1}$ 의 action $A'$ 은 alternative policy (target policy) $\pi$ 를 통해 선택

또한 Q-learning에서 behavior policy $\mu$ 는 $\epsilon$ -greedy, target policy $\pi$ 는 greedy control을 택하는 것이 가장 일반적이며, 이를 수식으로 표현하면 아래와 같다.

Q(S_t, A_t)\larr Q(S_t,A_t)+\alpha(R_{t+1}+\gamma Q(S_{t+1},A')-Q(S_t,A_t))

\text{, where }\gamma Q(S_{t+1},A')=\gamma Q(S_{t+1},argmax_{a'}Q(S_{t+1},a'))

\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }= max_{a'}\gamma Q(S_{t+1},a')

앞선 SARSA의 경우, next state $S_{t+1}$ 에서의 action $A'$ 를 behavior policy ( $\epsilon$ -greedy)로 sampling 하였음을 기억하자.

이처럼 Q-learning은 importance sampling을 하지 않아 likelihood ratio를 곱해줄 필요가 없고, off-policy MC/TD에 비해 variance를 낮출 수 있다는 장점이 있다. 또한 Q-learning이 SARSA와 비교하여 갖게 되는 다른 특징을 아래의 예시를 통해 살펴보자.

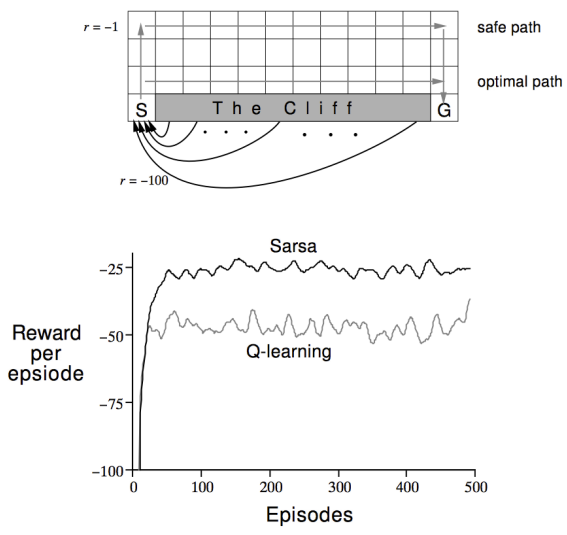
위 그림은 Richard S. Sutton의 [Reinforcement Learning: An Introduction] 교재에 소개되어 있는 'Cliff Walking' 예제이다. 좌측 하단의 start state S에서 우측 하단의 goal state G에 최단 거리로 도달하는 것이 목적이며, agent는 gridworld 상의 상하좌우로 이동할 수 있다. Cliff를 제외한 칸에 도달할 때마다 -1의 reward가 주어지며, cliff에 도달할 경우 -100의 reward를 받고 start state S로 되돌아간다. 이 때, $\epsilon=0.1$ 의 동일한 조건으로 SARSA와 Q-learning 방식의 agent를 각각 학습시켜 보았을 때 얻게 되는 return 값은 아래 그래프와 같다.

그래프에서 확인할 수 있듯이, SARSA로 학습된 agent가 평균적으로 더 높은 return 값을 얻게 된다. 하지만, cliff 근처 state의 Q-value function을 predict할 때, behavior policy ( $\epsilon$ -greedy)에 따른 기댓값을 계산하므로 cliff의 낮은 reward 값도 함께 반영돼 safe path를 찾는 경향성을 보이게 된다.

하지만 Q-learning의 경우, target policy (greedy)를 통해 Q-value function을 predict 하므로, cliff 근처 state에서도 cliff의 낮은 reward 값이 반영되지 않아 optimal path를 성공적으로 구할 수 있게 된다.

지금까지 MC, TD (SARSA), Q-learning 등의 학습 방법을 다뤄보았다. 이들은 유한한 state에 대한 value function을 예측, 저장해가며 optimal policy를 탐색하는 'tabular reinforcement learning'에 해당한다. 하지만, MDP의 차원이 커질수록 value function을 저장하기 위해 상당한 memory가 필요하고, 학습 소요시간도 크게 증가한다는 한계점이 있다.

특히 현실 세계로의 generalization을 위해선 사실상 개수가 무한대인 continuous state에 대해서도 학습할 수 있는 방법이 필요하다. 이를 위해 value function을 함수로 근사하는 value function approximation에 대해 다음 글에서 다뤄보도록 하겠다.