강화학습기초(6) - Value Function Approximation, Deep Q-Networks

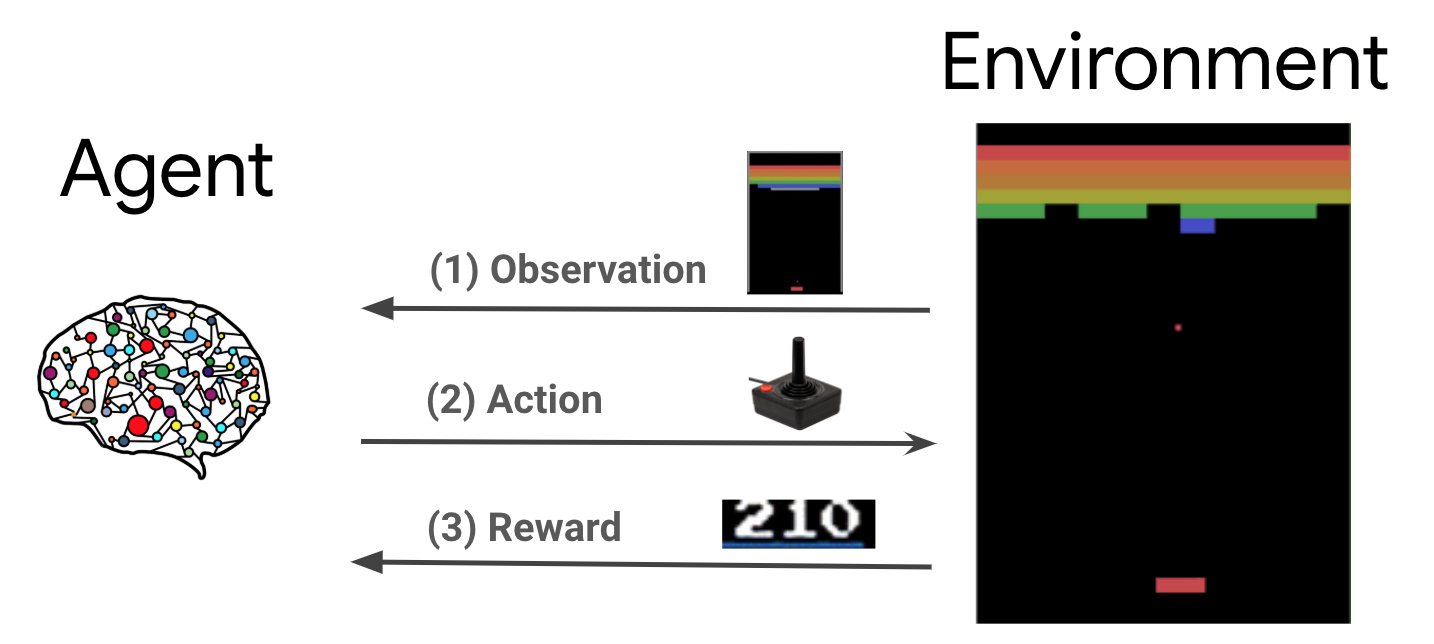
본 글에서는 value function approximation과 deep Q-networks (DQN)에 대해서 알아보도록 한다.

앞서 다룬 MC, TD (SARSA), Q-learning 등의 tabular reinforcement learning은 방대한 양의 data를 저장할 memory가 필요하고 학습 소요시간이 오래 걸린다는 단점이 있으며, 현실 세계의 continuous한 state에도 곧바로 적용시키지 못한다. 이에, value function의 값들을 일일히 저장할 필요 없이, 이를 출력해내는 함수로 근사하는 방법이 value function approximation이다.

Value Function Approximation

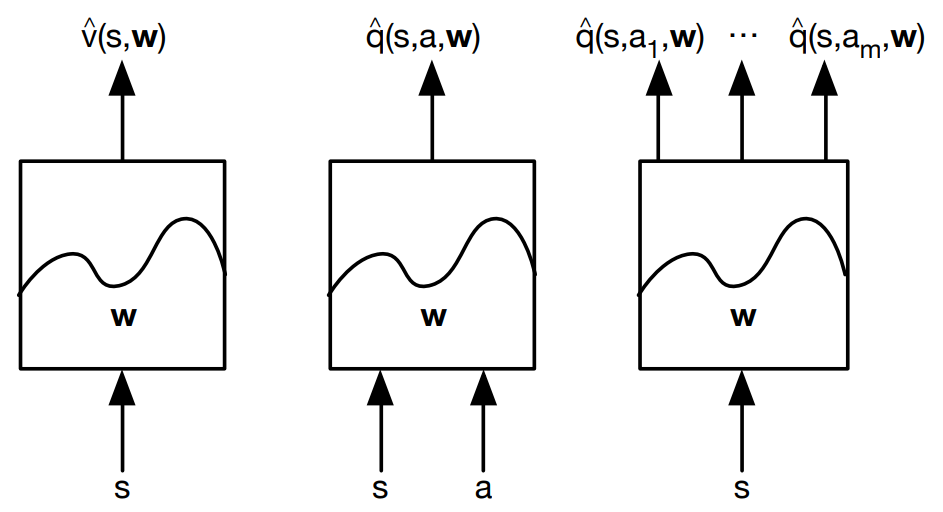
위와 같이, state $s$ 혹은 action $a$의 값을 받아 그에 해당하는 value function을 출력하는 function approximator를 정의할 수 있으며, 아래와 같이 수식으로 표현할 수 있다. (통계학에서 변수 위에 붙는 hat operator는 'estimator' 혹은 'estimated value'를 의미한다.)

이 때 state $s$와 action $a$는 함수에 입력될 수 있는 형태로 변환되어야 할 것이다.

예를 들어, agent가 상하좌우로 이동하여 목적지에 도달해야 하는 gridworld가 있다면, state는 (목적지와의 x좌표 차이, 목적지와의 y좌표 차이) 형태의 2차원 vector로, action은 (up, down, left, right, stay)로 정의된 action space에서의 index value로 정의될 수 있다.

이러한 function approximator를 통해, 학습 과정에서 경험해보지 못한 state에 대해서도 value function을 근사할 수 있게 되며, 이젠 학습을 통해 value function을 직접 predict하지 않는 대신, parameter $w$를 올바르게 update 해주어야 한다.

Gradient descent on RL

Parameter $w$는 $\hat{v}(s,w)$의 값이 true value function $v_\pi(s)$의 값을 approximate할 수 있도록 update되어야 하며, 이는 output이 dataset의 true label과 일치하도록 weight $w$를 학습시키는 supervised machine learning의 개념과 동일하다.

따라서 supervised learning에서와 같이, 학습의 방향을 제시하는 L2 loss function을 아래와 같이 생각해볼 수 있다.

하지만 supervised learning과는 달리, loss 값을 계산할 supervisor가 없으므로 $v_\pi(S)$ 값을 sampling하여 target으로 활용해야 한다. 이렇게 정의된 loss function에 gradient descent 기법을 적용하면 아래와 같다. ($\frac{1}{2}$의 계수는 단순히 L2 loss function의 제곱항에서 발생하는 계수 2를 소거시키기 위함이다.)

위 기댓값에 해당하는 부분은 sampling을 통해 얻어내야 하므로 gradient sample은 다음와 같아진다.

이 때, learning target에 해당하는 $v_\pi(S)$를 MC, TD(0), TD($\lambda$)의 target으로 치환해주면 각 학습방식에서 사용되는 gradient sample 식을 얻어낼 수 있다.

MC : $\Delta w=\alpha (G_t-\hat{v}(S_t,w))\nabla_w\hat{v}(S_t,w)$
TD(0) : $\Delta w=\alpha (R_{t+1}+\gamma\hat{v}(S_{t+1},w)-\hat{v}(S_t,w))\nabla_w\hat{v}(S_t,w)$
TD($\lambda$) : $\Delta w=\alpha (G_t^\lambda-\hat{v}(S_t,w))\nabla_w\hat{v}(S_t,w)$

State-value function에 대해 구해준 위 식을 model-free한 학습이 가능하도록 Q-value function으로 바꾸어줄 수 있으며, 그 과정을 정리하면 아래와 같다.
1. Q-value function approximation

2. Loss function

3. Stochastic gradient descent

여기서도 마찬가지로 MC, TD(0), TD($\lambda$)의 target을 대입해주면 최종적으로 각 학습방식에서 model-free하게 사용할 수 있는 gradient sample 수식을 도출해낼 수 있다.

MC : $\Delta w=\alpha (G_t-\hat{q}(S_t,A_t,w))\nabla_w\hat{q}(S_t,A_t,w)$
TD(0) : $\Delta w=\alpha (R_{t+1}+\gamma\hat{q}(S_{t+1}, A_{t+1},w)-\hat{q}(S_t,A_t,w))\nabla_w\hat{q}(S_t,A_t,w)$
TD($\lambda$) : $\Delta w=\alpha (G_t^\lambda-\hat{q}(S_t,A_t,w))\nabla_w\hat{v}(S_t,w)$

또한, eligibility trace가 고려된 backward-view of TD($\lambda$)도 아래와 같이 정의할 수 있다. 이 때, frequency heuristic이 $\nabla_w\hat{q}(S_t,A_t,w)$의 항으로 고려되었음에 유의하자.

정리하자면, MC와 TD에 function approximator를 적용하여, value function을 직접 predict하는 대신 이를 predict하는 parameter를 update하는 방식으로 학습을 진행한다. Policy control은 앞선 MC, TD에서와 같이 function approximator가 출력하는 value function을 기반으로 이뤄진다.

Batch reinforcement learning

MC와 TD에서 저장된 value function을 기반으로 action을 선택해가며 episode를 구성했듯이, value function approximation에서도 현재의 function approximator가 출력하는 value function으로 policy를 구성하여 training data를 sampling해나간다.

지금까지 다룬 방식은 기본적으로 한 episode (MC의 경우) 혹은 한 time-step (TD의 경우)에 대해 한 번의 update를 진행하는 stochastic gradient descent (SGD) 기법에 해당한다. 하지만 기존 supervised learning에서와 같이, 학습효율을 높이기 위해 batch 혹은 mini-batch method를 적용할 수도 있다.

하지만 training data를 학습과 동시에 생성해내는 value function approximation의 특성상, data efficiency가 더욱 중요한데, batch/mini-batch를 구성해 다수의 data를 동시에 사용하게 되면 필요한 data의 양이 그만큼 증가하여 data efficiency가 감소한다는 문제점이 있다. 또한 function parameter에 따라 data sample이 생성되는 on-policy 방식의 특성상 local optimum에도 쉽게 빠질 수 있다.

Experience replay

위 batch/mini-batch method의 문제점들을 해소하기 위해, experience replay를 사용할 수 있다. 이는 아래에서 살펴볼 Deep Q-Network의 논문에서 제시된 방법으로, 매 time-step마다 parameter update가 이루어지는 TD에서 활용할 수 있다.

우선 data sample을 $(s_t,a_t,r_{t+1},s_{t+1})$의 transition으로 time-step마다 끊어 모두 replay memory $D_i$에 저장한다. 이후 episode에 대한 data가 충분히 쌓이면, $D_i$에서 transition을 random하게 추출하여 mini-batch를 구성해 학습하는 방식이다. 이를 통해 여러 episode의 정보를 동시에 반영하여 특정 episode에 대한 dependency를 줄이고, local optimum에서 벗어날 수 있다.

또한 복원추출을 통해 하나의 data를 여러 번 활용함으로써 data efficiency 문제도 해결할 수 있다. 동일한 data가 추출되더라도 해당 mini-batch를 구성하는 나머지 data가 다르므로 새로운 update가 가능하다. Training iteration index를 $i$, 해당 iteration에서 구성된 mini-batch를 $D_i$라고 하면 experience replay를 적용한 loss function은 아래와 같은 수식으로 표현할 수 있다.

Deep Q-Networks (DQN)

Deep reinforcement learning (deepRL)

지금까지 value function을 approximate하는 function의 개념을 살펴보았다면, 이 function으로 deep neural network을 충분히 활용할 수 있고, 이를 deep reinforcement learning (deepRL)이라고 한다. 사실 value function뿐만 아니라 policy 자체를 approximate할 수도 있는데, 이는 후술하기로 하고 deepRL은 이들 모두를 총칭한다.

Deep Q-Networks (DQN)

특히, 2015년 DeepMind에서 개발한 DQN (Deep Q-Network)은 Q-learning에 CNN을 결합하여, Atari를 비롯한 다양한 게임을 단일 네트워크로 학습하여 훌륭한 성능을 이끌어내었다. 해당 논문의 알고리즘과 네트워크 도식은 아래와 같다.

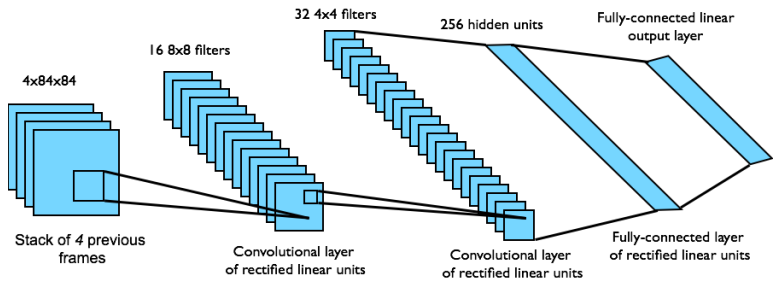
논문을 살펴보면, $210\times160$ pixel with 128 color의 입력 image를 gray-scale의 $84\times84$ region으로 preprocessing하여 CNN을 통과시켰으며, 후반부의 FC를 거쳐 출력된 vector가 game agent의 action에 대응됨을 알 수 있다. 이는 RL에 CNN 방법론을 적용하여 agent가 2D image이라는 high-dimensional data를 직접 다룰 수 있게 하였음에 큰 의의를 갖는다.

하지만 이처럼 Q-value function을 approximate한 뒤 greedy하게 policy를 수립할 경우, 특정 state에 대해 action이 하나로 결정되는 deterministic model이 되어버린다. 하지만 가위바위보와 같이 optimal policy가 stochastic한 경우(가위, 바위, 보를 random하게 내는 것이 optimal), 위 방법으로는 학습이 불가능하다.

이러한 문제점은 function approximator가 value function이 아닌 policy 자체를 approximate하게 함으로써 해결할 수 있는데, 이를 policy gradient라 칭하고 다음 글에서 알아보도록 하겠다.

---

References

• UCL Course on RL, David Silver
• Reinforcement Learning: An Introduction, Richard S. Sutton
• Fundamental of Reinforcement Learning, 이웅원
• Playing Atari with Deep Reinforcement Learning, DeepMind