[Linear Algebra] Geometric Span Vector Equation

Geometric Description of Span

e.g.

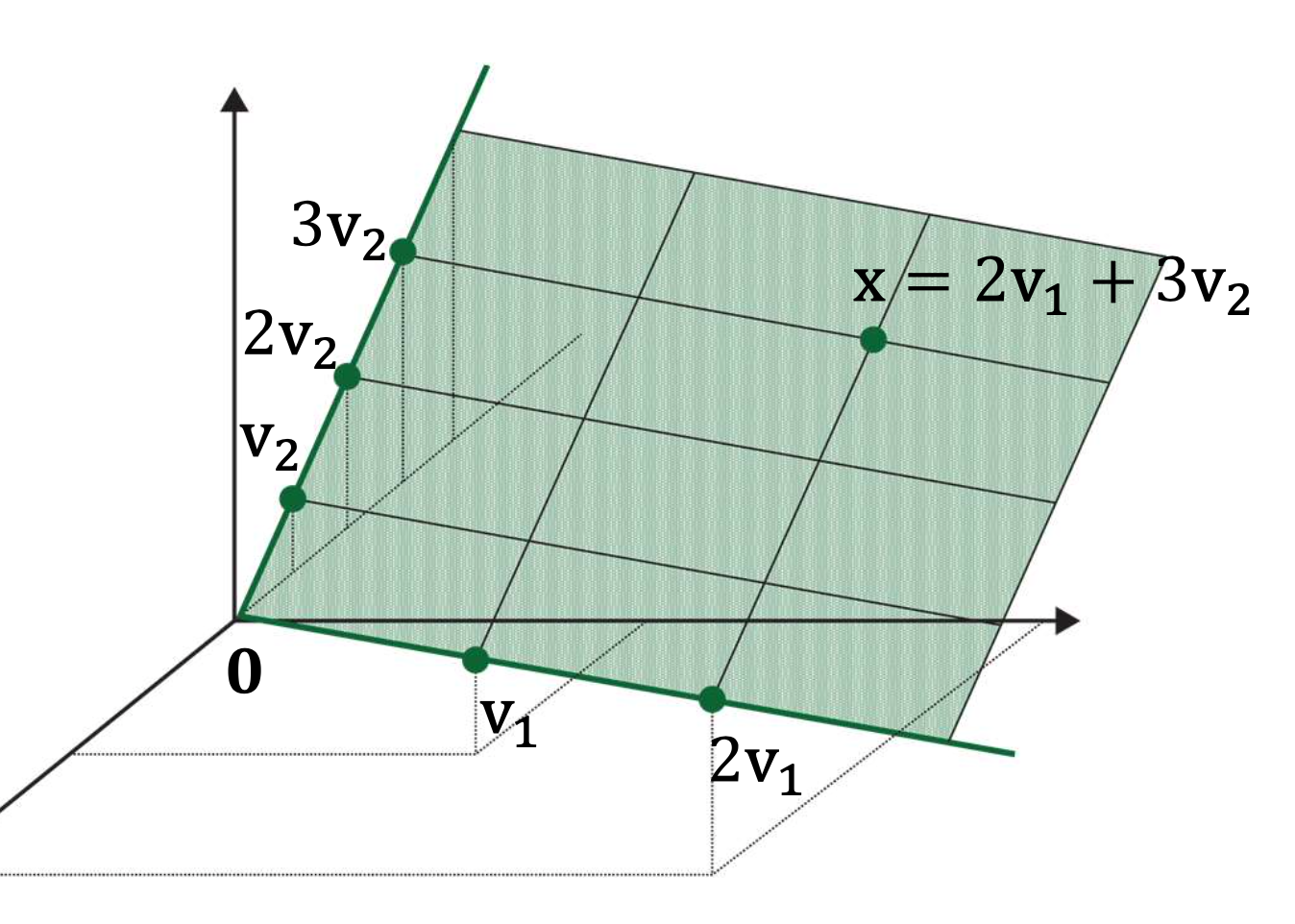
if $\textbf{v}_1$ and $\textbf{v}_2$ are nonzero vectors in $\mathbb{R}^{3}$, with $\textbf{v}_2$ not a multiple of $\textbf{v}_1$

then $\textrm{Span}\begin{Bmatrix} \textbf{v}_1, \textbf{v}_2 \end{Bmatrix}$ is the plane in $\mathbb{R}^{3}$ that contains $\textbf{v}_1, \textbf{v}_2$ and $\textbf{0}$

Geometric Interpretation of Vector Equation

• Finding a linear combination of given vectors $\textbf{a}_1, \textbf{a}_2,$ and $\textbf{a}_3$ to be equal to $\textbf{b}$
• The solution exists only when $\textbf{b} \in \textrm{Span}\begin{Bmatrix} \textbf{a}_1, \textbf{a}_2, \textbf{a}_3 \end{Bmatrix}$

e.g.
$2 x_1 + 2 x_2 + 1 x_3 = 6$
$3 x_1 + 1 x_2 + 0 x_3 = 14$
$1 x_1 + 3 x_2 + 1 x_3 = 18$

$\begin{bmatrix} 2\\ 3\\ 1\end{bmatrix} x_1 + \begin{bmatrix} 2\\ 1\\ 3\end{bmatrix} x_2 + \begin{bmatrix} 1\\ 0\\ 1\end{bmatrix} x_3 = \begin{bmatrix} 6\\ 14\\ 18\end{bmatrix}$

if $\begin{bmatrix} 6\\ 14\\ 18\end{bmatrix} \in \textrm{Span}\begin{Bmatrix} \begin{bmatrix} 2\\ 3\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ 1\\ 3\end{bmatrix}, \begin{bmatrix} 1\\ 0\\ 1\end{bmatrix} \end{Bmatrix}$, then solution exist