Hi! I'm Jaylnne. ✋

캐글에서 제공하는 Credit Card Fraud Detection Dataset 으로 신용카드 사기 탐지 모델을 만들고, 각 방법론의 성능을 비교 평가한 결과를 공유합니다.

1. Dataset

---

사용하고자 하는 데이터는 2013년 9월 유럽의 신용카드 사용자들의 실제 총 284, 807 건의 거래내역입니다. 이 중 492 건이 사기 거래(Fraud Transaction)이고 사기 거래가 정상 거래에 비해 매우 적은 비중으로 포함되어 있는 'Hightly unbalanced'한 특징을 가진 데이터셋입니다. 확인해보니, Class 가 1에 해당하는 데이터의 비율이 전체의 약 0.17% 남짓밖에 되지 않는군요.

import pandas as pd

df = pd.read_csv('creditcard.csv')

tmp = df['Class'].value_counts().to_frame().reset_index()
tmp['Percent(%)'] = tmp["Class"].apply(lambda x : round(100*float(x) / len(df), 2))
tmp = tmp.rename(columns = {"index" : "Target", "Class" : "Count"})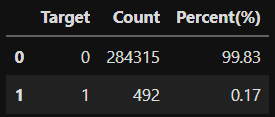

데이터의 각 컬럼 정보는 아래와 같습니다.

V1 ~ V28 : 개인정보로 공개되지 않은 값
Time : 시간
Amount : 거래금액
Class : 사기 여부 (1: 사기, 0: 정상)

따라서 컬럼의 개수는 총 31개이며, 이 정보들을 활용하여 사기 여부(Class)를 예측하는 모델을 만들어 볼 예정입니다.

2. EDA

---

2-1. Null 확인

null 값은 존재하지 않는 것으로 확인했습니다.

df.isnull().sum().max()

# output
0

2-2. Class 분포 확인

이미 위에서 value_counts 로 클래스의 분포를 확인해보았지만, 이를 막대 그래프로 시각화하여 다시 한번 확인해봅시다.

import matplotlib.pyplot as plt
plt.style.use('seaborn')

bar_df = df['Class'].value_counts().reset_index()
plt.title('Class Distributions', fontsize=20)
plt.bar(
    bar_df['index'], 
    bar_df['Class'], 
    color=['red', 'blue'], 
    tick_label=['fraud', 'normal']
)
plt.xlabel('fraud of normal transaction')
plt.show()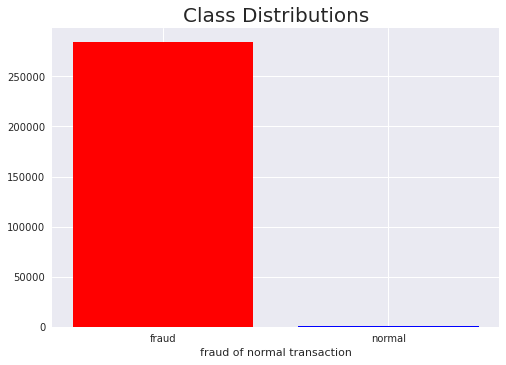

2-3. 거래 금액 & 거래 시간

2-3-1. 분포 확인

거래 금액(Amount)와 거래 시간(Time)의 분포를 확인해보니, 거래 금액의 규모는 상대적으로 매우 작은 편이고, 거래가 많이 이루어지는 시간대와 그렇지 않은 시간대가 상당히 구분되어 있음을 알 수 있습니다.

amount_val = df['Amount'].values
time_val = df['Time'].values

plt.subplots(constrained_layout=True)

plt.subplot(2, 1, 1)
plt.title('Transaction Amount Distribution')
plt.hist(amount_val, bins=50)

plt.subplot(2, 1, 2)
plt.title('Transaction Time Distribution')
plt.hist(time_val, bins=50)

plt.show()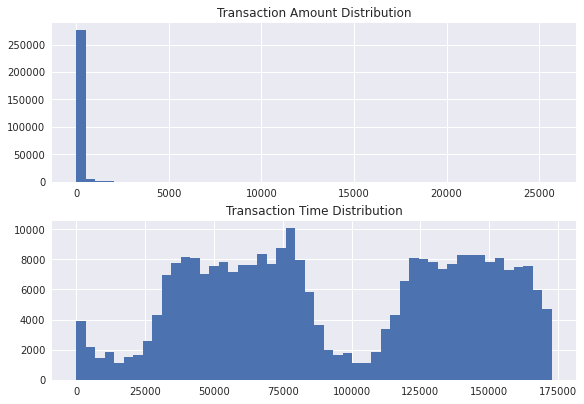

2-3-2. Scaling

df.describe()로 확인해보니, V1~28은 값이 이미 scaling 되어 있는 것으로 보입니다. 그러나 Amount 와 Time 은 위 분포로 보아 그렇지 않기 때문에, Scaling 을 진행해보도록 하겠습니다.

스케일러는 RobustScaler 를 선택했습니다. StandardScaler 와 MinmaxScaler 의 선택지도 있지만, RobustScaler 가 outlier 에 조금 더 견고한 알고리즘이기 때문에 이를 택했습니다. Amount 의 경우 outlier 와 평균치의 거리가 매우 먼 것을 위 그래프로 미리 확인했기 때문입니다.

from sklearn.preprocessing import RobustScaler

rob_scaler = RobustScaler()

df['scaled_amount'] = rob_scaler.fit_transform(df['Amount'].values.reshape(-1, 1))
df['scaled_time'] = rob_scaler.fit_transform(df['Time'].values.reshape(-1, 1))

df.drop(['Time', 'Amount'], axis=1, inplace=True)

plt.subplots(constrained_layout=True)

plt.subplot(2, 1, 1)
plt.title('Transaction Scaled Amount Distribution')
plt.hist(df['scaled_amount'].values, bins=50)

plt.subplot(2, 1, 2)
plt.title('Transaction Scaled Time Distribution')
plt.hist(df['scaled_time'].values, bins=50)

plt.show()

scaling 완료된 Amount 와 Time 의 분포를 확인해보면 아래와 같습니다. 분포의 형태는 이전과 달라지지 않은 듯 보이지만, x축의 값을 확인해보면 scaling 전에 비해 분산이 상당히 줄었음을 알 수 있습니다.

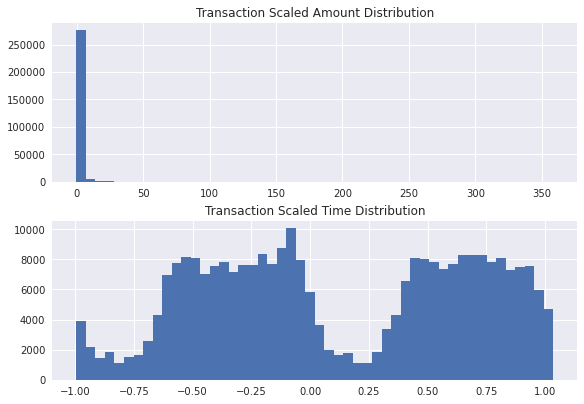
3. Class Imbalance 문제 해결 방법

데이터의 클래스 불균형이 심각하다는 사실을 여러 차례 확인했습니다. 그렇다면 이러한 Class Imbalance 문제를 어떻게 해결해야할 지 고민해야합니다. Class Imbalance 문제를 해결하는 방법으로는 Over Sampling 과 Under Sampling 이 있습니다. 따라서 두 가지 방법을 모두 활용하여 그 결과를 비교해보도록 하겠습니다.

3-1. Trainset, Test 분리

Under Sampling 을 진행하기 이전에, Over Sampling 에 활용할 train dataset 과 test dataset 을 미리 분리하여 저장해두도록 하겠습니다.

from sklearn.model_selection import train_test_split

X = df.drop('Class', axis=1)
y = df['Class']

original_Xtrain, original_Xtest, original_ytrain, original_ytest = train_test_split(
    X, 
    y, 
    test_size=0.2, 
    shuffle=True, 
    stratify=y, 
    random_state=42,
)

original_Xtrain.to_csv('data/original_Xtrain.csv', index=False)
original_Xtest.to_csv('data/original_Xtest.csv', index=False)
original_ytrain.to_csv('data/original_ytrain.csv', index=False)
original_ytest.to_csv('data/original_ytest.csv', index=False)

3-2. Under Sampling

사기 거래 데이터 수가 492개인 것을 확인했으므로, 1:1 비율을 맞추어주기 위해 정상 거래 데이터도 492개만 랜덤 샘플링해보겠습니다.

❗ Under Sampling 은 매우 간단하게 활용 가능한 방법이지만, '정보의 소실' 이 발생할 수 있다는 점을 항상 유의해야 합니다. 이번 프로젝트에서만 보더라도 284, 315 개의 정상 거래 데이터 중 샘플링 되지 못한 나머지 283, 823 개의 데이터는 사용하지 않게 되는 것이니까요.

df = df.sample(frac=1, random_state=42)

fraud_df = df.loc[df['Class'] == 1]
normal_df = df.loc[df['Class'] == 0][:492]

df = pd.concat([fraud_df, normal_df])
df = df.sample(frac=1, random_state=42, ignore_index=True)

클래스 분포가 1:1로 잘 맞추어졌는지 다시금 막대 그래포로 확인해봅시다.

bar_df = df['Class'].value_counts().reset_index()
plt.title('Class Distributions', fontsize=20)
plt.bar(bar_df['index'], 
        bar_df['Class'], 
        color=['red', 'blue'], 
        tick_label=['fraud', 'normal']
       )
plt.xlabel('fraud of normal transaction')
plt.show()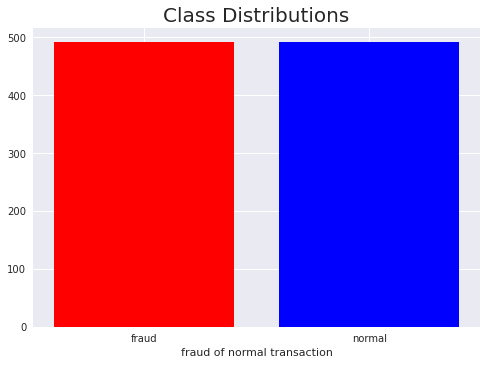

3-2-1. Correlation of Features 확인

Under Sampling 을 통해 Class Imabalance 문제를 해결했으니, 해당 데이터로 각 feature 들 간의 상관관계를 확인해봅시다. 히트맵을 이용하면 정보를 한 눈에 파악할 수 있습니다.

import numpy as np

corr = df.corr()

fig, ax = plt.subplots(1, 1, figsize=(15, 15))
img = ax.imshow(corr, cmap='magma', interpolation='nearest', aspect='auto')
ax.set_xticks(np.arange(len(corr.columns)), labels=list(corr.columns))
ax.set_yticks(np.arange(len(corr.columns)), labels=list(corr.columns))
plt.setp(ax.get_xticklabels(), rotation=45, ha="right", rotation_mode="anchor")
plt.colorbar(img)
plt.show()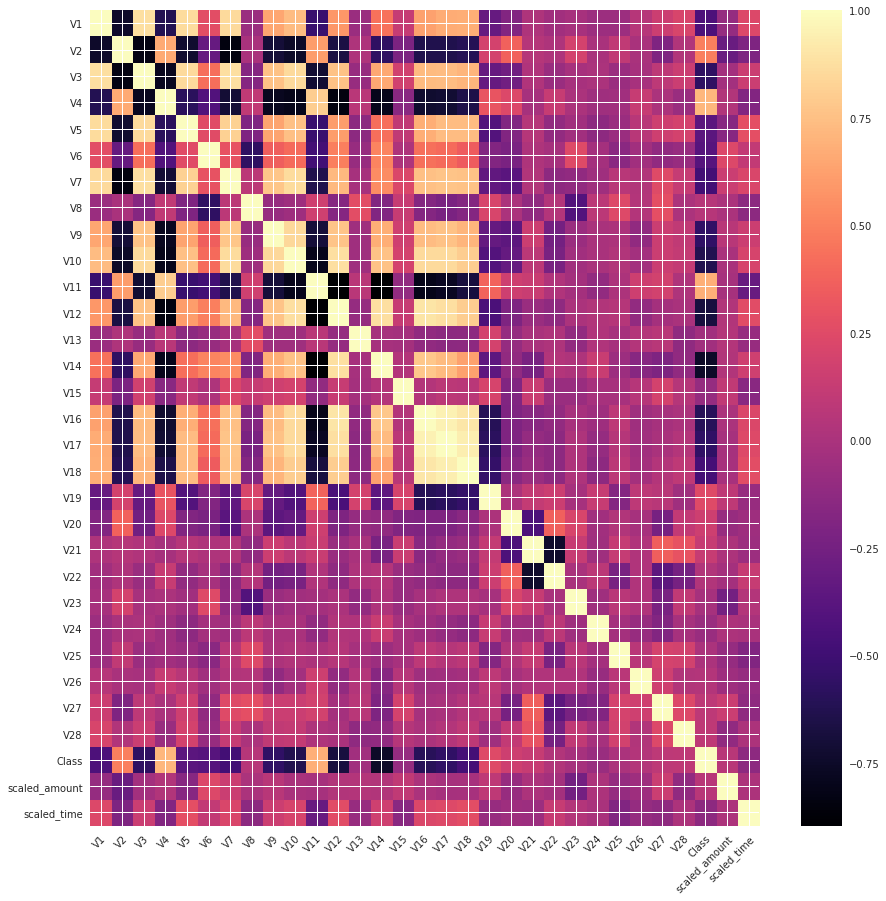

히트맵을 분석해보면 아래와 같이 정리할 수 있습니다.

• 강한 음의 상관관계
  • V17, V14, V12, V10
• 강한 양의 상관관계
  • V2, V4, V11, V19

Box Plot 을 그려 양의 상관관계가 있는 feature 들과 음의 상관관계가 있는 feature 들의 분포를 Class 와 비교하여 봅시다.

import seaborn as sns

fig, ax = plt.subplots(1, 4, figsize=(25, 5))

# .subplot(1, 4, 1)
sns.boxplot(x="Class", y="V17", data=df, palette=['red', 'blue'], ax=ax[0])
ax[0].set_title('V17 vs Class Negative Correlation')

sns.boxplot(x="Class", y="V14", data=df, palette=['red', 'blue'], ax=ax[1])
ax[1].set_title('V14 vs Class Negative Correlation')


sns.boxplot(x="Class", y="V12", data=df, palette=['red', 'blue'], ax=ax[2])
ax[2].set_title('V12 vs Class Negative Correlation')


sns.boxplot(x="Class", y="V10", data=df, palette=['red', 'blue'], ax=ax[3])
ax[3].set_title('V10 vs Class Negative Correlation')

plt.show()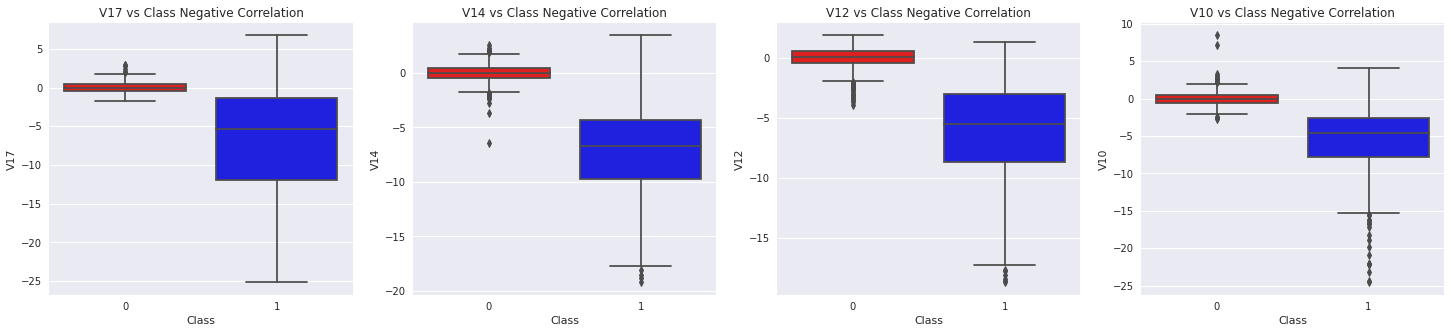

fig, ax = plt.subplots(1, 4, figsize=(25, 5))

sns.boxplot(x="Class", y="V11", data=df, palette=['red', 'blue'], ax=ax[0])
ax[0].set_title('V11 vs Class Positive Correlation')

sns.boxplot(x="Class", y="V4", data=df, palette=['red', 'blue'], ax=ax[1])
ax[1].set_title('V4 vs Class Positive Correlation')


sns.boxplot(x="Class", y="V2", data=df, palette=['red', 'blue'], ax=ax[2])
ax[2].set_title('V2 vs Class Positive Correlation')


sns.boxplot(x="Class", y="V19", data=df, palette=['red', 'blue'], ax=ax[3])
ax[3].set_title('V19 vs Class Positive Correlation')

plt.show()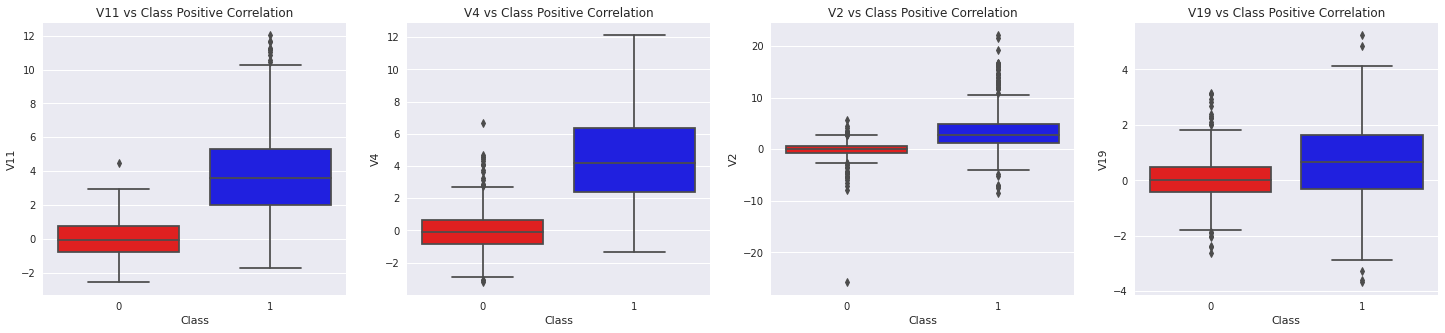

3-2-2. Outlier 제거

Class 결정에 높은 영향을 미칠 feature 들이 무엇일지 확인해보았습니다. 그렇다면 해당 feature 들에서 모델 학습에 혼란을 줄 수 있는 outlier 들을 제거해보겠습니다.

v17_fraud = df['V17'].loc[df['Class'] == 1].values
q25, q75 = np.percentile(v17_fraud, 25), np.percentile(v17_fraud, 75)
v17_iqr = q75 - q25

v17_cut_off = v17_iqr * 1.5
v17_lower, v17_upper = q25 - v17_cut_off, q75 + v17_cut_off
print('v17 Lower: {}'.format(v17_lower))
print('v17 Upper: {}'.format(v17_upper))
outliers = [x for x in v17_fraud if x < v17_lower or x > v17_upper]
print('Feature v17 Outliers for Fraud Cases: {}'.format(len(outliers)))
print('V17 outliers: {}'.format(outliers))
df = df.drop(df[(df['V17'] > v17_upper) | (df['V17'] < v17_lower)].index)
print('Number of Instances after outliers removal: {}\n'.format(len(df)))

v14_fraud = df['V14'].loc[df['Class'] == 1].values
q25, q75 = np.percentile(v14_fraud, 25), np.percentile(v14_fraud, 75)
v14_iqr = q75 - q25

v14_cut_off = v14_iqr * 1.5
v14_lower, v14_upper = q25 - v14_cut_off, q75 + v14_cut_off
print('Cut Off: {}'.format(v14_cut_off))
print('V14 Lower: {}'.format(v14_lower))
print('V14 Upper: {}'.format(v14_upper))
outliers = [x for x in v14_fraud if x < v14_lower or x > v14_upper]
print('Feature V14 Outliers for Fraud Cases: {}'.format(len(outliers)))
print('V14 outliers:{}'.format(outliers))
df = df.drop(df[(df['V14'] > v14_upper) | (df['V14'] < v14_lower)].index)
print('Number of Instances after outliers removal: {}\n'.format(len(df)))

v12_fraud = df['V12'].loc[df['Class'] == 1].values
q25, q75 = np.percentile(v12_fraud, 25), np.percentile(v12_fraud, 75)
v12_iqr = q75 - q25

v12_cut_off = v12_iqr * 1.5
v12_lower, v12_upper = q25 - v12_cut_off, q75 + v12_cut_off
print('V12 Lower: {}'.format(v12_lower))
print('V12 Upper: {}'.format(v12_upper))
outliers = [x for x in v12_fraud if x < v12_lower or x > v12_upper]
print('Feature V12 Outliers for Fraud Cases: {}'.format(len(outliers)))
print('V12 outliers: {}'.format(outliers))
df = df.drop(df[(df['V12'] > v12_upper) | (df['V12'] < v12_lower)].index)
print('Number of Instances after outliers removal: {}\n'.format(len(df)))

v10_fraud = df['V10'].loc[df['Class'] == 1].values
q25, q75 = np.percentile(v10_fraud, 25), np.percentile(v10_fraud, 75)
v10_iqr = q75 - q25

v10_cut_off = v10_iqr * 1.5
v10_lower, v10_upper = q25 - v10_cut_off, q75 + v10_cut_off
print('V10 Lower: {}'.format(v10_lower))
print('V10 Upper: {}'.format(v10_upper))
outliers = [x for x in v10_fraud if x < v10_lower or x > v10_upper]
print('Feature V10 Outliers for Fraud Cases: {}'.format(len(outliers)))
print('V10 outliers: {}'.format(outliers))
df = df.drop(df[(df['V10'] > v10_upper) | (df['V10'] < v10_lower)].index)
print('Number of Instances after outliers removal: {}'.format(len(df)))

# output
v17 Lower: -27.84973307168096
v17 Upper: 14.562735952416062
Feature v17 Outliers for Fraud Cases: 0
V17 outliers: []
Number of Instances after outliers removal: 984

Cut Off: 8.114853173228278
V14 Lower: -17.807576138200663
V14 Upper: 3.8320323237414122
Feature V14 Outliers for Fraud Cases: 4
V14 outliers:[-19.2143254902614, -18.0499976898594, -18.4937733551053, -18.8220867423816]
Number of Instances after outliers removal: 980

V12 Lower: -17.3430371579634
V12 Upper: 5.776973384895937
Feature V12 Outliers for Fraud Cases: 4
V12 outliers: [-18.6837146333443, -18.5536970096458, -18.0475965708216, -18.4311310279993]
Number of Instances after outliers removal: 976

V10 Lower: -14.89885463232024
V10 Upper: 4.92033495834214
Feature V10 Outliers for Fraud Cases: 27
V10 outliers: [-15.5637913387301, -22.1870885620007, -24.4031849699728, -15.2399619587112, -16.3035376590131, -15.5637913387301, -18.9132433348732, -15.1241628144947, -22.1870885620007, -16.6496281595399, -22.1870885620007, -16.7460441053944, -16.6011969664137, -17.1415136412892, -18.2711681738888, -16.2556117491401, -15.1237521803455, -15.3460988468775, -14.9246547735487, -15.2399619587112, -22.1870885620007, -20.9491915543611, -19.836148851696, -15.2318333653018, -24.5882624372475, -14.9246547735487, -23.2282548357516]
Number of Instances after outliers removal: 947

Box Plot 을 그려보면 극심한 outlier 값들이 다소 제거된 것을 확인할 수 있습니다. (V17 은 제거된 outlier 가 없으므로 V14, V12, V10 만 확인해봅니다.)

f,(ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(20,6))

colors = ['green', 'orange']

# V14
sns.boxplot(x="Class", y="V14", data=df, ax=ax1, palette=colors)
ax1.set_title("V14 Feature \n Reduction of outliers", fontsize=14)
ax1.annotate('Less extreme \n outliers', xy=(0.98, -17.5), xytext=(0, -12),
            arrowprops=dict(facecolor='black'),
            fontsize=14)

# V12
sns.boxplot(x="Class", y="V12", data=df, ax=ax2, palette=colors)
ax2.set_title("V12 Feature \n Reduction of outliers", fontsize=14)
ax2.annotate('Less extreme \n outliers', xy=(0.98, -17.3), xytext=(0, -12),
            arrowprops=dict(facecolor='black'),
            fontsize=14)

# V10
sns.boxplot(x="Class", y="V10", data=df, ax=ax3, palette=colors)
ax3.set_title("V10 Feature \n Reduction of outliers", fontsize=14)
ax3.annotate('Less extreme \n outliers', xy=(0.95, -16.5), xytext=(0, -12),
            arrowprops=dict(facecolor='black'),
            fontsize=14)

plt.show()

3-2-3. 차원 축소 & 클러스터링

여기까지 전처리를 거친 데이터셋으로 클러스터링을 진행해봅시다. feature 들이 Class 를 구분하기 위한 유의미한 정보를 담고 있는지 확인해볼 수 있을 것입니다. (만약, 클러스터링한 결과 Class 간의 feature 분포가 지나치게 모호하게 나타나면 해당 데이터셋의 분류 모델 학습은 실험을 진행해보지 않아도 결과가 좋지 않을 것임을 짐작할 수 있습니다.)

--> 창배님의 피드백대로, feature 들이 유의미한 정보를 담고 있는지 아닌지 여부는 굳이 차원 축소와 클러스터링을 거쳐 시각화해보지 않아도 Classification 모델의 학습 결과로서 곧장 확인할 수 있습니다. 그러나 학습을 진행하기 이전에 결과를 시각적으로 한번 확인해보고 싶었던 차원으로 이해해주시면 감사하겠습니다.

--> 흠... 그렇지만, 분명, 차원 축소와 클러스터링의 결과를 Classification 에 활용하지 못한 것은 피드백대로 고민이 되는 부분입니다. 리서치를 조금 더 진행해서 고도화를 시도해보도록 하겠습니다. 😚

차원 축소의 개념이 낯선 분들은 간단하게 아래 그림을 이해해주시면 됩니다. 2차원의 데이터를 1차원으로 차원 축소한 간단한 예를 그림으로 표현한 것입니다.

차원 축소 기법으로 많이 알려진 t-SNE, PCA, TruncatedSVD 3 가지를 적용해 각각의 결과를 확인해보겠습니다.

import time
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA, TruncatedSVD

X = df.drop('Class', axis=1)
y = df['Class']

# T-SNE Implementation
t0 = time.time()
X_reduced_tsne = TSNE(n_components=2, random_state=42).fit_transform(X.values)
t1 = time.time()
print(f'T-SNE 소요 시간: {t1 - t0:.2} s')

# PCA Implementation
t0 = time.time()
X_reduced_pca = PCA(n_components=2, random_state=42).fit_transform(X.values)
t1 = time.time()
print(f'PCA 소요 시간: {t1 - t0:.2} s')

# TruncatedSVD
t0 = time.time()
X_reduced_svd = TruncatedSVD(n_components=2, algorithm='randomized', random_state=42).fit_transform(X.values)
t1 = time.time()
print(f'TruncatedSVD 소요 시간: {t1 - t0:.2} s')

# output

T-SNE 소요 시간: 2.7 s
PCA 소요 시간: 0.06 s
TruncatedSVD 소요 시간: 0.012 s

import matplotlib.patches as mpatches

f, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(24,6))
f.suptitle('Clusters after Dimension Reduction', fontsize=14)

blue_patch = mpatches.Patch(color='blue', label='No Fraud')
red_patch = mpatches.Patch(color='red', label='Fraud')

# t-SNE
ax1.scatter(X_reduced_tsne[:,0], X_reduced_tsne[:,1], c=(y == 0), cmap='coolwarm', label='No Fraud', linewidths=2)
ax1.scatter(X_reduced_tsne[:,0], X_reduced_tsne[:,1], c=(y == 1), cmap='coolwarm', label='Fraud', linewidths=2)
ax1.set_title('t-SNE', fontsize=14)
ax1.grid(True)
ax1.legend(handles=[blue_patch, red_patch])


# PCAs
ax2.scatter(X_reduced_pca[:,0], X_reduced_pca[:,1], c=(y == 0), cmap='coolwarm', label='No Fraud', linewidths=2)
ax2.scatter(X_reduced_pca[:,0], X_reduced_pca[:,1], c=(y == 1), cmap='coolwarm', label='Fraud', linewidths=2)
ax2.set_title('PCA', fontsize=14)
ax2.grid(True)
ax2.legend(handles=[blue_patch, red_patch])

# TruncatedSVD
ax3.scatter(X_reduced_svd[:,0], X_reduced_svd[:,1], c=(y == 0), cmap='coolwarm', label='No Fraud', linewidths=2)
ax3.scatter(X_reduced_svd[:,0], X_reduced_svd[:,1], c=(y == 1), cmap='coolwarm', label='Fraud', linewidths=2)
ax3.set_title('Truncated SVD', fontsize=14)
ax3.grid(True)
ax3.legend(handles=[blue_patch, red_patch])

plt.show()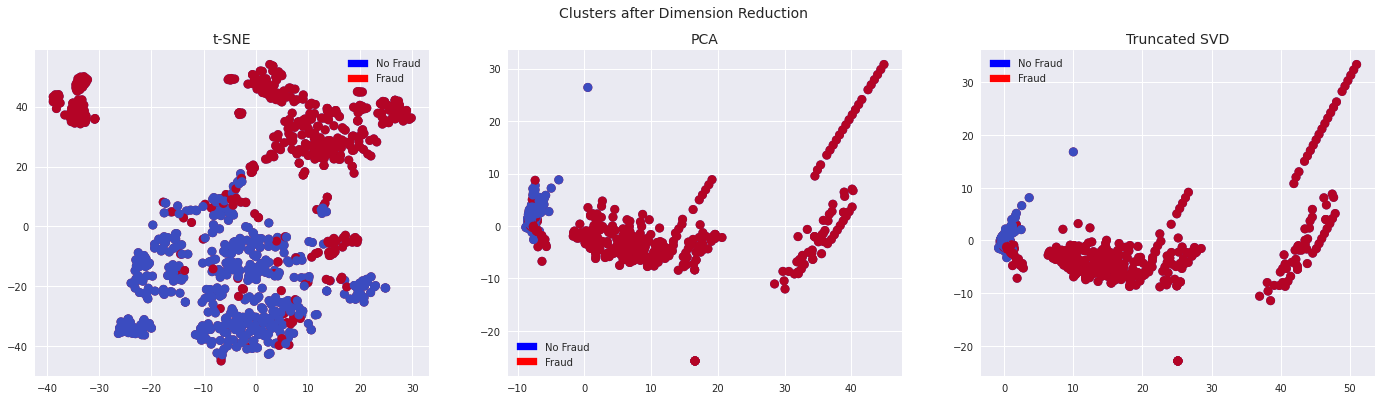

t-SNE 의 결과를 보면, 클래스별 feature 가 잘 구분되어 있음을 확인할 수 있습니다.

3-2-4. Classification

여기까지 진행된 데이터에 Classification 알고리즘을 적용해보겠습니다. Over Sampling 이 아닌 Under Sampling 된 데이터에만 Classification 을 먼저 진행해보는 이유는, 이번 과정에서 확인된 best hyper-parameter 정보를 Over Sampling 단계에서 활용하기 위함입니다.

Classification 알고리즘은 Logistic Regression, K-Nearest Neighbor, Support Vector Machine, Decision Tree 4 가지를 적용해 각 결과를 확인해보겠습니다.

from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier

X = df.drop('Class', axis=1)
y = df['Class']

X_train, X_test, y_train, y_test = train_test_split(
    X, 
    y, 
    test_size=0.2, 
    shuffle=True, 
    stratify=y, 
    random_state=42,
)

# Logistic Regression 
log_reg_params = {"penalty": ['l2'], 'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000]}
grid_log_reg = GridSearchCV(LogisticRegression(max_iter=3000), log_reg_params)
grid_log_reg.fit(X_train, y_train)
log_reg = grid_log_reg.best_estimator_

# K-Nearest
knears_params = {"n_neighbors": list(range(2,5,1)), 'algorithm': ['auto', 'ball_tree', 'kd_tree', 'brute']}
grid_knears = GridSearchCV(KNeighborsClassifier(), knears_params)
grid_knears.fit(X_train, y_train)
knears_neighbors = grid_knears.best_estimator_

# Support Vector Classifier
svc_params = {'C': [0.5, 0.7, 0.9, 1], 'kernel': ['rbf', 'poly', 'sigmoid', 'linear']}
grid_svc = GridSearchCV(SVC(), svc_params)
grid_svc.fit(X_train, y_train)
svc = grid_svc.best_estimator_

# DecisionTree Classifier
tree_params = {"criterion": ["gini", "entropy"], "max_depth": list(range(2,4,1)), 
              "min_samples_leaf": list(range(5,7,1))}
grid_tree = GridSearchCV(DecisionTreeClassifier(), tree_params)
grid_tree.fit(X_train, y_train)
tree_clf = grid_tree.best_estimator_

# corrected mistake ;)
log_reg_score = cross_val_score(log_reg, X_train, y_train, cv=5)
# log_reg_score = cross_val_score(log_reg, X_test, y_test, cv=5)
print('Logistic Regression Cross Validation Score: ', round(log_reg_score.mean() * 100, 2).astype(str) + '%')

# corrected mistake ;)
knears_score = cross_val_score(knears_neighbors, X_train, y_train, cv=5)
# knears_score = cross_val_score(knears_neighbors, X_test, y_test, cv=5)
print('Knears Neighbors Cross Validation Score', round(knears_score.mean() * 100, 2).astype(str) + '%')

# corrected mistake ;)
svc_score = cross_val_score(svc, X_train, y_train, cv=5)
# svc_score = cross_val_score(svc, X_test, y_test, cv=5)
print('Support Vector Classifier Cross Validation Score', round(svc_score.mean() * 100, 2).astype(str) + '%')

# corrected mistake ;)
tree_score = cross_val_score(tree_clf, X_train, y_train, cv=5)
# tree_score = cross_val_score(tree_clf, X_test, y_test, cv=5)
print('DecisionTree Classifier Cross Validation Score', round(tree_score.mean() * 100, 2).astype(str) + '%')

# output

Logistic Regression Cross Validation Score:  90.0%
Knears Neighbors Cross Validation Score 88.42%
Support Vector Classifier Cross Validation Score 88.42%
DecisionTree Classifier Cross Validation Score 88.42%

Logistic Regression 의 결과가 94.98% 로 가장 좋은 것을 확인할 수 있습니다.

정정) 위와 같이 train dataset 의 validation accuracy 만으로 성능을 비교하여 모델을 선택한 것은 적절하지 않았습니다. 만약 validation accuracy 로 평가를 진행하려 했다면 이 이후에도 일관성있게 validation accuracy 를 참고했어야 하는데, 뒤에서는 test accuracy 를 참고해 모델의 성능을 평가했기 때문입니다. 😅 애초에 여기서의 의도도 test accuracy 를 보려던 것이었습니다. 피곤했는지... 코드 작성 중에 실수를 했네요. 정정한 비교 결과는 다음 포스팅, 신용카드 사기 거래 탐지 모델 (2) 에 포함하겠습니다. 참고로 test accuracy 상으로도 Logistic Regression 이 가장 나은 성능을 보였습니다.

from sklearn.metrics import roc_auc_score
from sklearn.model_selection import cross_val_predict


log_reg_pred = cross_val_predict(log_reg, X_train, y_train, cv=5, method="decision_function")
knears_pred = cross_val_predict(knears_neighbors, X_train, y_train, cv=5)
svc_pred = cross_val_predict(svc, X_train, y_train, cv=5, method="decision_function")
tree_pred = cross_val_predict(tree_clf, X_train, y_train, cv=5)

print('Logistic Regression: ', roc_auc_score(y_train, log_reg_pred))
print('KNears Neighbors: ', roc_auc_score(y_train, knears_pred))
print('Support Vector Classifier: ', roc_auc_score(y_train, svc_pred))
print('Decision Tree Classifier: ', roc_auc_score(y_train, tree_pred))

# output

Logistic Regression:  0.9424356699201419
KNears Neighbors:  0.8811002661934338
Support Vector Classifier:  0.927240461401952
Decision Tree Classifier:  0.8715616681455192

AUC (Area Under Curve) 를 기준으로 확인해보아도 마찬가지의 결과를 얻을 수 있습니다.

3-3. Over Sampling (SMOTE)

Over Sampling 의 방법론으로는 SMOTE 를 활용해보겠습니다. Over Sampling 에도 다양한 기법들이 존재하지만, SMOTE 가 좋은 성능을 낸 케이스를 최근 많이 보아 해당 기법을 택했습니다. Classification 은 Under Sampling 데이터에서 가장 좋은 성능을 냈던 Logistic Regression 으로 계속해서 진행해보겠습니다.

다만, 모델의 파라미터는 Under Sampling 의 best_estimator_ 와 Over Sampling 의 best_estimator_ 를 각각 적용해 정확도를 비교해보도록 하겠습니다.

❗ Under Sampling 로 학습한 모델의 best parameters 를 적용해본다는 의미입니다. 데이터는 아까 미리 분리하여 저장해두었던 original_Xtrain.csv, original_Xtest.csv, original_ytrain.csv, original_ytest.csv 를 사용합니다.

3-3-1. Under Sampling 학습 모델

3-2-4. Classification 에서 추출했던 log_reg(= grid_log_reg.best_estimator_) 즉, Under Sampling 데이터로 학습한 best parameters 를 적용해봅시다.

from imblearn.over_sampling import SMOTE

sm = SMOTE(sampling_strategy='auto', random_state=42)
Xsm_train, ysm_train = sm.fit_resample(original_Xtrain, original_ytrain)

log_reg_sm = log_reg
log_reg_sm.fit(Xsm_train, ysm_train)

결과를 confusion matrix 로 확인해보면 아래와 같습니다.

from sklearn.metrics import confusion_matrix

y_pred_log_reg = log_reg_sm.predict(X_test)
log_reg_cf = confusion_matrix(y_test, y_pred_log_reg)

fig, ax = plt.subplots(1, 1, figsize=(22,12))
                       
sns.heatmap(log_reg_cf, ax=ax, annot=True, cmap=plt.cm.copper)
ax.set_title("Logistic Regression \n Confusion Matrix", fontsize=20)
ax.set_xticklabels(['', ''], fontsize=20, rotation=90)
ax.set_yticklabels(['', ''], fontsize=20, rotation=360)
plt.show()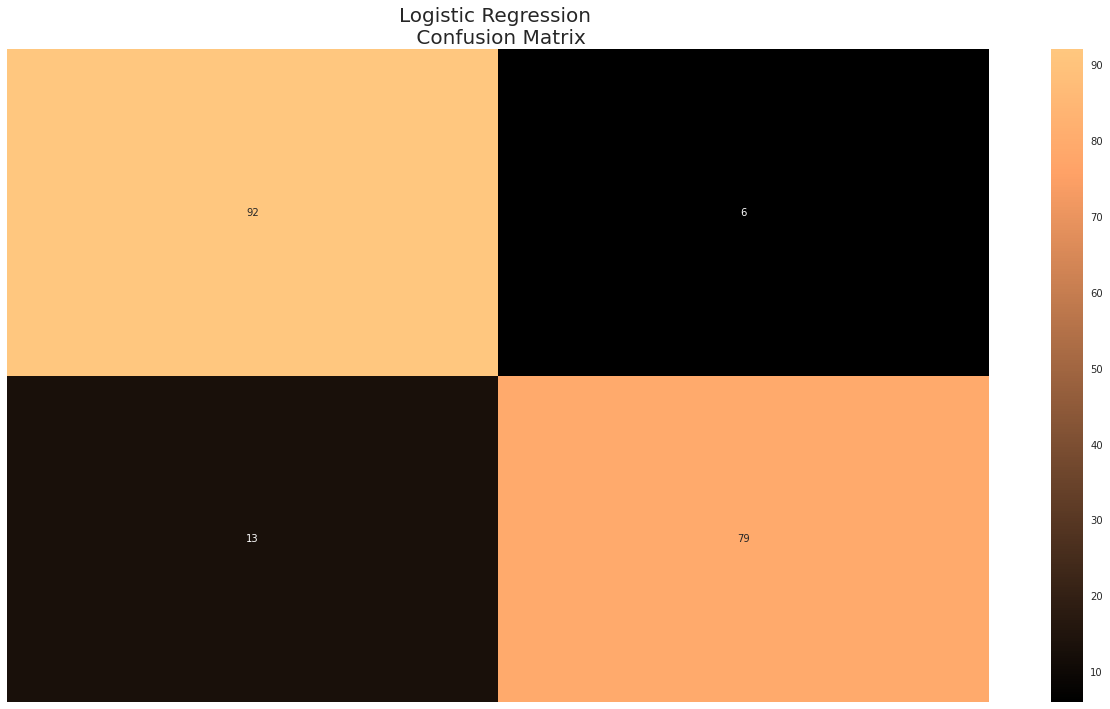

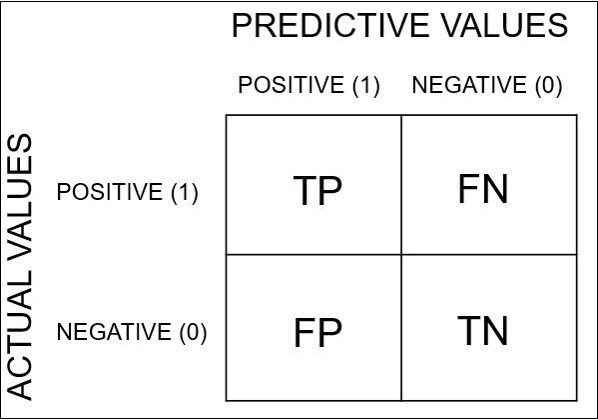
위 confusion matrix 는 아래 이미지를 참고하여 이해하면 됩니다.

3-3-2. Over Sampling 데이터 학습

이번에는 Over Sampling 한 데이터로 모델을 학습해, best_estimator_ 즉, best parameters 값을 구해봅시다.

from sklearn.model_selection import RandomizedSearchCV
from imblearn.pipeline import make_pipeline as imbalanced_make_pipeline

rand_log_reg = RandomizedSearchCV(
    LogisticRegression(max_iter=3000), 
    log_reg_params, 
    n_iter=4, 
    error_score='raise'
)

log_reg_params = {"penalty": ['l2'], 'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000]}
# SMOTE 를 미리 실행했던 `3-3-1.` 과정과 달리, 
# 여기서는 SMOTE Over Sampling 이 여기서 동시에 진행됩니다.
pipeline = imbalanced_make_pipeline(SMOTE(sampling_strategy='auto'), rand_log_reg)
model = pipeline.fit(original_Xtrain, original_ytrain)
best_est = rand_log_reg.best_estimator_

3-3-3. Under Sampling 과 Over Sampling 의 best_estimator_ 결과 비교

from sklearn.metrics import accuracy_score

# Logistic Regression with Under Sampling
y_pred = log_reg.predict(X_test)
undersample_score = accuracy_score(y_test, y_pred)

# Logistic Regression with Over Sampling (SMOTE)
y_pred_sm = best_est.predict(original_Xtest)
oversample_score = accuracy_score(original_ytest, y_pred_sm)

d = {'Technique': ['Random UnderSampling', 'Oversampling (SMOTE)'], 'Score': [undersample_score, oversample_score]}
final_df = pd.DataFrame(data=d)

score = final_df['Score']
final_df.drop('Score', axis=1, inplace=True)
final_df.insert(1, 'Score', score)

final_df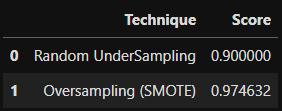

Over Sampling 데이터로 학습한 Logistic Regrsssion 모델의 결과가 더 좋았음을 확인할 수 있었습니다.

4. 3-layer Neural Network

현재까지 진행한 실험 결과만으로는 SMOTE 로 Over Sampling 한 데이터를 Logistic Regression 모델에 학습시킨 결과가 가장 좋았다고 말할 수 있습니다.

그렇다면 이번에는 딥러닝 기법을 활요해보면 어떨까요? 3-Layer Dense Neural Network 를 쌓아, 딥러닝 모델의 Classification 결과도 확인해봅시다.

4-1. Under Sampling 데이터 학습 결과

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Activation, Dense
from tensorflow.keras.optimizers import Adam

n_inputs = X_train.shape[1]

undersample_model = Sequential([
    Dense(n_inputs, input_shape=(n_inputs, ), activation='relu'),
    Dense(32, activation='relu'),
    Dense(2, activation='softmax')
])

undersample_model.summary()
undersample_model.compile(Adam(lr=0.001), loss='sparse_categorical_crossentropy', metrics=['accuracy'])
undersample_model.fit(
    X_train, 
    y_train, 
    validation_split=0.2, 
    batch_size=32,
    epochs=15,
    shuffle=True, 
    verbose=2,
)
undersample_predictions = undersample_model.predict(original_Xtest, batch_size=200, verbose=0)
undersample_fraud_predictions = undersample_model.predict_classes(original_Xtest, batch_size=200, verbose=0)

# output

Model: "sequential_7"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_21 (Dense)             (None, 30)                930       
_________________________________________________________________
dense_22 (Dense)             (None, 32)                992       
_________________________________________________________________
dense_23 (Dense)             (None, 2)                 66        
=================================================================
Total params: 1,988
Trainable params: 1,988
Non-trainable params: 0
_________________________________________________________________
Epoch 1/15
19/19 - 1s - loss: 0.5696 - accuracy: 0.6975 - val_loss: 0.3829 - val_accuracy: 0.7697
Epoch 2/15
19/19 - 0s - loss: 0.3744 - accuracy: 0.8430 - val_loss: 0.2725 - val_accuracy: 0.9145
Epoch 3/15
19/19 - 0s - loss: 0.2954 - accuracy: 0.8975 - val_loss: 0.2196 - val_accuracy: 0.9342
Epoch 4/15
19/19 - 0s - loss: 0.2422 - accuracy: 0.9339 - val_loss: 0.1889 - val_accuracy: 0.9408
Epoch 5/15
19/19 - 0s - loss: 0.2032 - accuracy: 0.9388 - val_loss: 0.1640 - val_accuracy: 0.9408
Epoch 6/15
19/19 - 0s - loss: 0.1766 - accuracy: 0.9438 - val_loss: 0.1473 - val_accuracy: 0.9408
Epoch 7/15
19/19 - 0s - loss: 0.1560 - accuracy: 0.9537 - val_loss: 0.1351 - val_accuracy: 0.9539
Epoch 8/15
19/19 - 0s - loss: 0.1390 - accuracy: 0.9570 - val_loss: 0.1270 - val_accuracy: 0.9539
Epoch 9/15
19/19 - 0s - loss: 0.1271 - accuracy: 0.9587 - val_loss: 0.1216 - val_accuracy: 0.9474
Epoch 10/15
19/19 - 0s - loss: 0.1166 - accuracy: 0.9554 - val_loss: 0.1196 - val_accuracy: 0.9474
Epoch 11/15
19/19 - 0s - loss: 0.1079 - accuracy: 0.9620 - val_loss: 0.1156 - val_accuracy: 0.9474
Epoch 12/15
19/19 - 0s - loss: 0.1003 - accuracy: 0.9620 - val_loss: 0.1157 - val_accuracy: 0.9474
Epoch 13/15
19/19 - 0s - loss: 0.0947 - accuracy: 0.9636 - val_loss: 0.1148 - val_accuracy: 0.9474
Epoch 14/15
19/19 - 0s - loss: 0.0896 - accuracy: 0.9686 - val_loss: 0.1160 - val_accuracy: 0.9474
Epoch 15/15
19/19 - 0s - loss: 0.0855 - accuracy: 0.9686 - val_loss: 0.1176 - val_accuracy: 0.9474

4-2. Over Sampling 데이터 학습 결과

n_inputs = Xsm_train.shape[1]

oversample_model = Sequential([
    Dense(n_inputs, input_shape=(n_inputs, ), activation='relu'),
    Dense(32, activation='relu'),
    Dense(2, activation='softmax')
])

oversample_model.compile(Adam(lr=0.001), loss='sparse_categorical_crossentropy', metrics=['accuracy'])
oversample_model.fit(
    Xsm_train, 
    ysm_train, 
    validation_split=0.2, 
    batch_size=300, 
    epochs=15, 
    shuffle=True, 
    verbose=2
)
oversample_predictions = oversample_model.predict(original_Xtest, batch_size=200, verbose=0)
oversample_fraud_predictions = oversample_model.predict_classes(original_Xtest, batch_size=200, verbose=0)

# output

Epoch 1/15
1214/1214 - 3s - loss: 0.0792 - accuracy: 0.9705 - val_loss: 0.0317 - val_accuracy: 0.9906
Epoch 2/15
1214/1214 - 3s - loss: 0.0178 - accuracy: 0.9951 - val_loss: 0.0165 - val_accuracy: 0.9983
Epoch 3/15
1214/1214 - 3s - loss: 0.0096 - accuracy: 0.9978 - val_loss: 0.0105 - val_accuracy: 0.9993
Epoch 4/15
1214/1214 - 3s - loss: 0.0064 - accuracy: 0.9985 - val_loss: 0.0041 - val_accuracy: 0.9999
Epoch 5/15
1214/1214 - 3s - loss: 0.0046 - accuracy: 0.9990 - val_loss: 0.0017 - val_accuracy: 1.0000
Epoch 6/15
1214/1214 - 3s - loss: 0.0037 - accuracy: 0.9992 - val_loss: 0.0020 - val_accuracy: 0.9999
Epoch 7/15
1214/1214 - 3s - loss: 0.0031 - accuracy: 0.9993 - val_loss: 0.0023 - val_accuracy: 0.9998
Epoch 8/15
1214/1214 - 3s - loss: 0.0029 - accuracy: 0.9994 - val_loss: 0.0015 - val_accuracy: 1.0000
Epoch 9/15
1214/1214 - 3s - loss: 0.0024 - accuracy: 0.9995 - val_loss: 7.1552e-04 - val_accuracy: 1.0000
Epoch 10/15
1214/1214 - 3s - loss: 0.0022 - accuracy: 0.9995 - val_loss: 0.0017 - val_accuracy: 1.0000
Epoch 11/15
1214/1214 - 3s - loss: 0.0020 - accuracy: 0.9996 - val_loss: 0.0014 - val_accuracy: 0.9998
Epoch 12/15
1214/1214 - 3s - loss: 0.0019 - accuracy: 0.9996 - val_loss: 4.3326e-04 - val_accuracy: 1.0000
Epoch 13/15
1214/1214 - 3s - loss: 0.0015 - accuracy: 0.9997 - val_loss: 5.4413e-04 - val_accuracy: 1.0000
Epoch 14/15
1214/1214 - 3s - loss: 0.0017 - accuracy: 0.9996 - val_loss: 3.4783e-04 - val_accuracy: 1.0000
Epoch 15/15
1214/1214 - 3s - loss: 0.0016 - accuracy: 0.9996 - val_loss: 0.0010 - val_accuracy: 1.0000

Over Sampling 데이터로 학습한 3-Layer NN 모델의 경우 Epoch 5 즈음부터 val_accuracy 가 거의 100% 를 달성함을 확인할 수 있었습니다. 🤗 태스크마다, 데이터마다 적절한 모델을 항상 다른 법이지만, 역시 NN 은 강력하군요!

여기까지, 실제 신용카드 거래 내역 데이터로 Fraud Detection 을 진행해보았습니다. 질문이나 잘못된 내용이 있으면 댓글로 알려주세요. 감사합니다! 🙇‍♀️

5. Next to Do

• 각 전처리와 모델들을 python 모듈화 하기
• BentoML 로 도커라이징 후 API 띄워보기
• JMeter 로 API 성능 테스트 해보기

몇 가지 개선 사항을 다음 포스팅에 포함하였습니다. 계속해서 (2), (3), (4) 로 이어질 예정입니다.

• [ML] 신용카드 사기 거래 탐지 모델 만들어보기 (2)