[CS224W] 12. Network Effects and Cascading Behavior

.·2021년 4월 5일

CS224W : GNN

목록 보기

11/12

Contents

Intro : Spreading Through Networks

Decision Based Model of Diffusion

Extending the Model : Allow People to Adopt A and B

Summary : behavior 는 network 안에서 전파된다 ( cascading ) ~

0. Intro : Spreading Through Networks

Behaviors that cascade from node to node like an epidemic
Behaviors 는 node 에서 node 로, 쭉쭉 전파된다

Cascading Behavior (행동 전파), Diffusion of Innovations (혁신이 퍼져 나가는 것), Network Effects, Epidemics (전염병) 등이 이에 해당된다 ~

우리는 실생활에서 다음과 같은 Cascading 의 예시들을 볼 수 있다

Biological : 전염병
Technological
- Cascading Failure : 부품이 하나 고장나면, 다 고장 나는 것
- Spread of Information : 기술 전파
Social
- Rumors, News, New Technology : 소문, 뉴스
- Viral Marketing : 입소문 마케팅

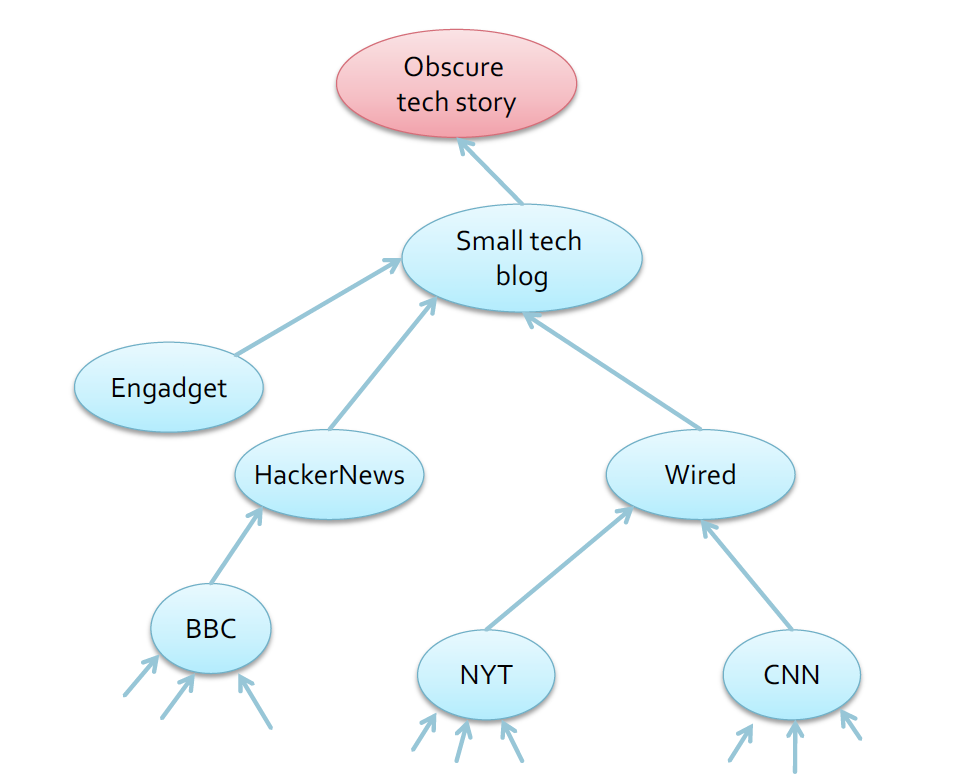
Information Diffusion 은, 작은 tech story 에서 시작되어서 → 어떤 사람이 본인의 small tech blog 에 이를 소개하고 → tech news platform 에서 이를 발견해서 소개하고 → 이를 완전 크고 유명한 news broadcast platform 에서 발견해서 소개하는 방식으로 진행된다 ~

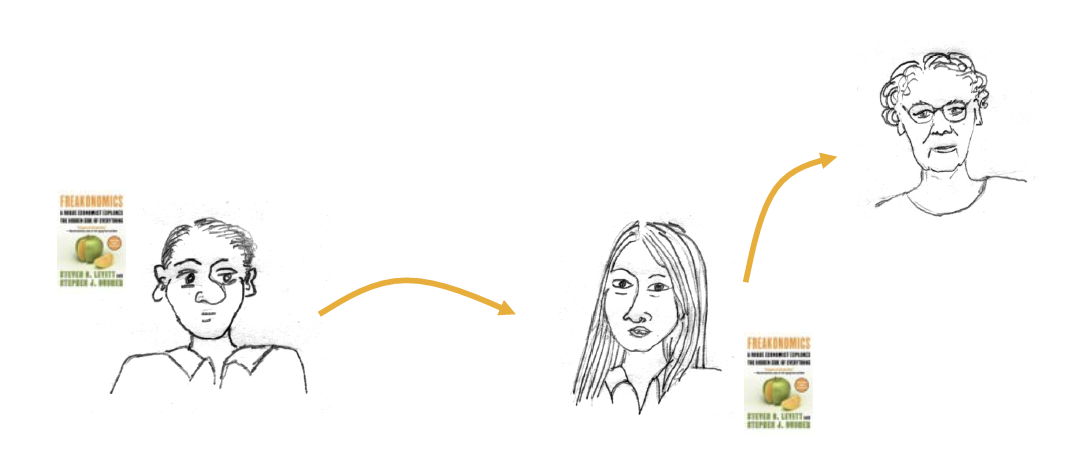
Viral Marketing 의 경우, 나의 preference & feedback 이 옆 사람에게 전달되고, 전달 받은 사람이 또 전달하여 해당 상품에 대한 정보가 다양한 사람들에게 전파되게 된다

Twitter & Facebook 의 Post Sharing 의 경우에도, 내가 공유한 것을 친구가 공유하고, 이를 다른 사람이 공유하는 식으로 전파된다

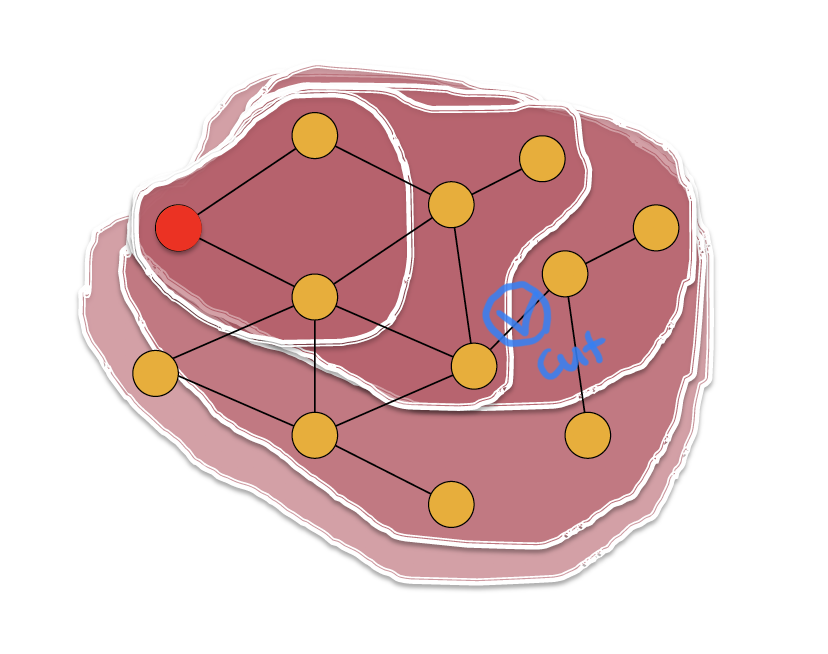
위의 그림은 Disease 가 전파되는 양상을 보여 주고 있는데,
위의 예시들과 마찬가지로 타고 타고 전파되기 때문에, 전염병의 확산을 막기 위해서는 연결 고리를 파악하고 끊는 것이 중요하다고 한다
(그치만 이게 쉽지 않은 것이 함정 ㅠ_ㅠ ~~~)

Network Cascades

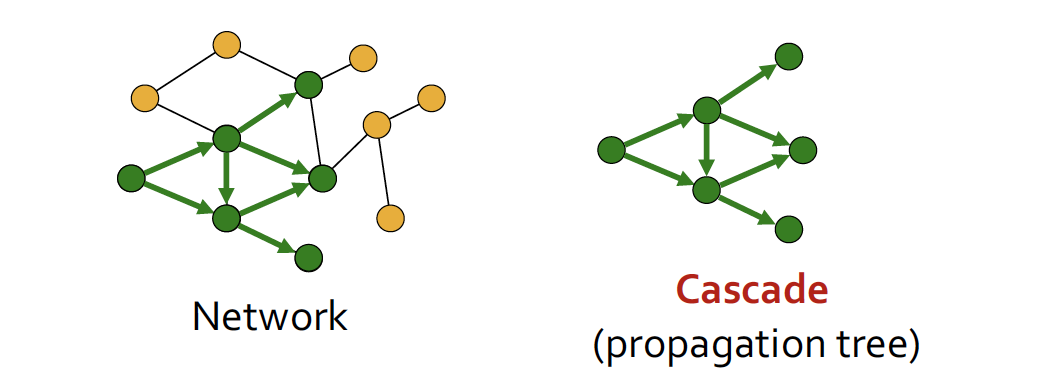
우리는 지금까지 (왼쪽 그림) Network 에 대해 공부했다 ~
이번 강의에서는, Network 내의 node 에서 node 로 행동이 전파되는, propagation tree 인 Cascade 에 대해 배운다 ~

How Do We Model Diffusion?

Decision Based Model
- each node decides whether to activate based on its neighbors’ decisions
- 전파 여부를 결정할 수 있는, Decision Making 선택권이 있는 모델
- node 는 active player 가 된다
- ex. 기술 채택, 물건 구매 결정
Probablistic Model
- infected nodes “push” contagion to uninfected nodes with some probability.
- 결정권이 없는, 확률에 의해 전파 여부가 결정되는 모델
- nodes 는 passive player 가 된다
- ex. corona..... ㅠ_ㅠ

이번 12강에서 공부하는 diffusion model 은 Decision Based Model 이다 ~

1. Decision Based Model of Diffusion

Game Theoretic Model of Cascades

Decision Based Model 은 Game Theory 를 바탕으로 진행된다!

✔︎ Game Theory (from wikipedia)
개인 또는 기업이 어떠한 행위를 했을 때, 그 결과가 게임에서와 같이 자신뿐만 아니라 다른 참가자의 행동에 의해서도 결정되는 상황에서, 자신의 최대 이익에 부합하는 행동을 추구한다는 수학적 이론!

죄수의 딜레마가 대표적인 게임이론의 예시...
캐나다에서 수업으로 들었었는데, 각잡고 공부해보니 겁나 어려웠던 기억.. ㅎㅅㅎ

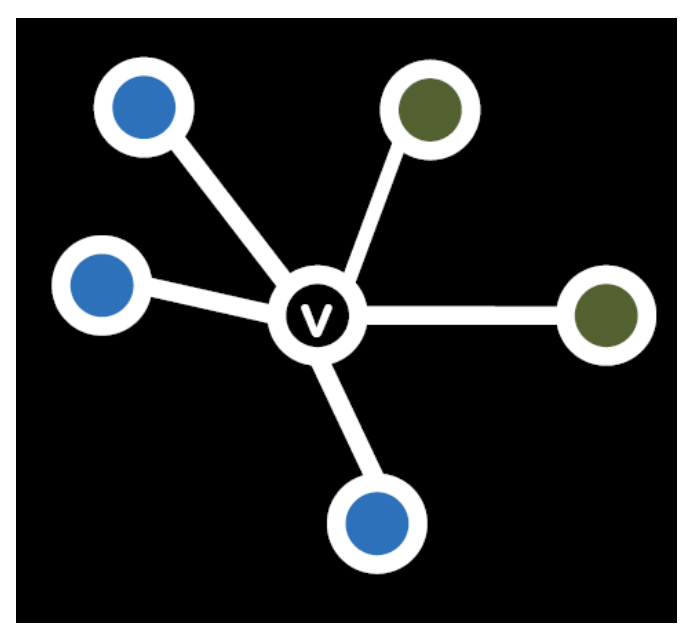
2명의 player 가 각각 A 혹은 B 의 선택을 한다고 할 때,
나랑 같은 선택을 하는 친구가 많을수록 내가 payoff 를 더 많이 받는다
따라서 위의 그림에서는 파란색을 선택하게 될 것 ~

VHS vs BetaMax 와 BlueRay vs HD DVD 상황에서도,
많은 사람들이 주류로 사용했던 VHS, BlueRay 만 살아남게 되었다고 한다

The Model for Two Nodes

payoff matrix

v 와 w 가 모두 behavior A 를 선택한다면, payoff a > 0 획득한다
v 와 w 가 모두 behavior B 를 선택한다면, payoff b > 0 획득한다
v 와 w 가 서로 다른 행동을 선택한다면, payoff = 0 획득한다

최종 payoff 는 전체 게임 결과의 payoff 들의 합으로 계산된다!

Calculation of Node v

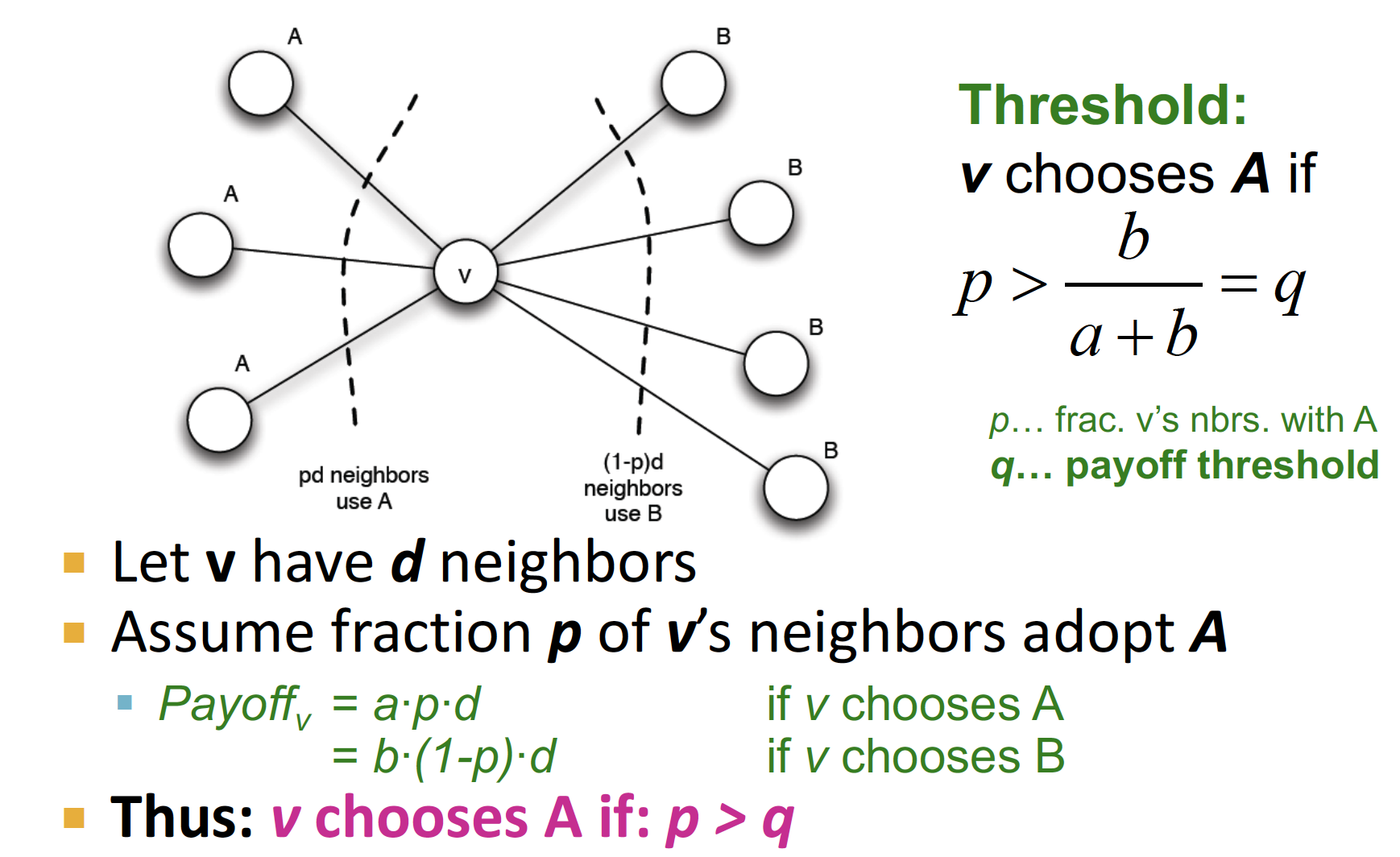
v 가 behavior A 를 선택하게 되려면,
$a \cdot p \cdot d$ (A를 선택했을 때 받는 payoff) > $b \cdot (1-p) \cdot d$ (B를 선택했을 때 받는 payoff) 가 되어야 한다

즉, 식을 다시 정리해 보면 ~
$a \cdot p \cdot d > b \cdot (1-p) \cdot d$
$\Leftrightarrow \frac{p}{1-p} > \frac{b \cdot d}{a \cdot d}$
$\Leftrightarrow a \cdot p > b \cdot (1-p)$
$\Leftrightarrow (a+b) \cdot p > b$
$\therefore p > \frac{b}{a+b} = q$

따라서 Threshold 는 위와 같이 설정 되고, $p>q$ 일 때 A를 선택하게 된다
(근데 이거 당연한 소리 아닌감 ......)

Example Scenario

A가 전파되는 양상을 살펴 보고자 한다 ~

모든 Node 는 B 에서 시작한다
작은 집단 S = {u, v} 만 A를 일찍 적용한다
- Hard-wire S : 보상에 상관없이 A를 꾸준히 선택하는 집단
  ex. 갤럭시 러버, 🍎 농장 주주
neighborhood 50% 이상이 A를 선택하면, 나도 A 를 선택한다
(단, A 와 B 의 payoff 가 비슷한 상황에서!)

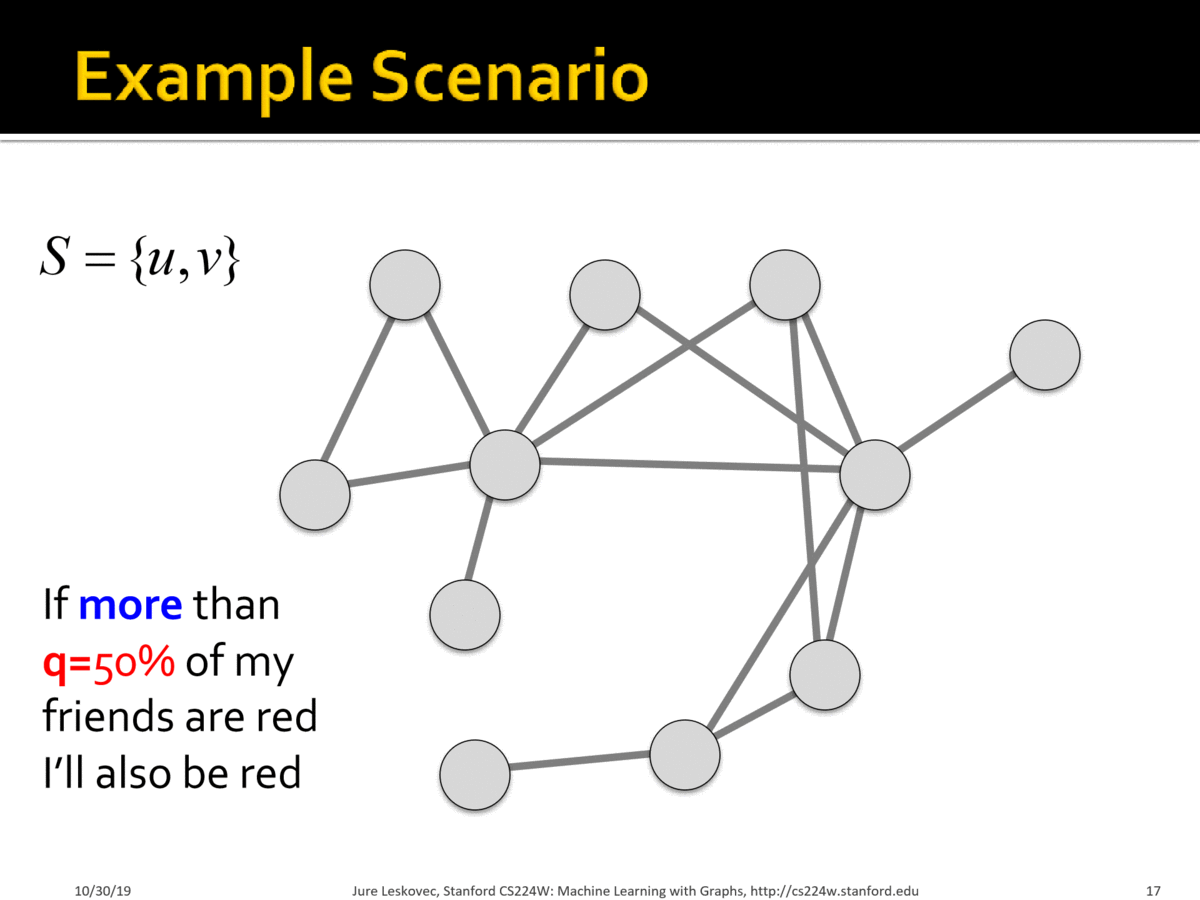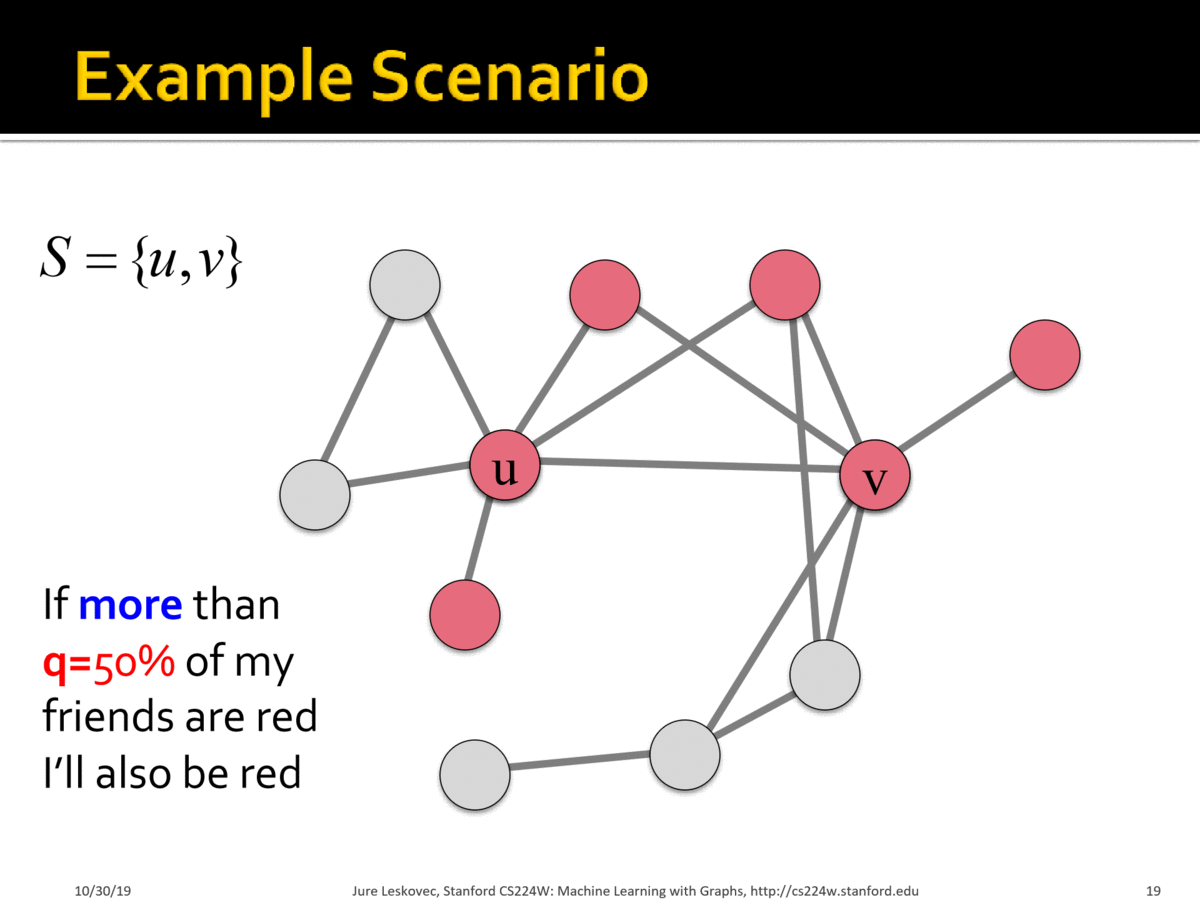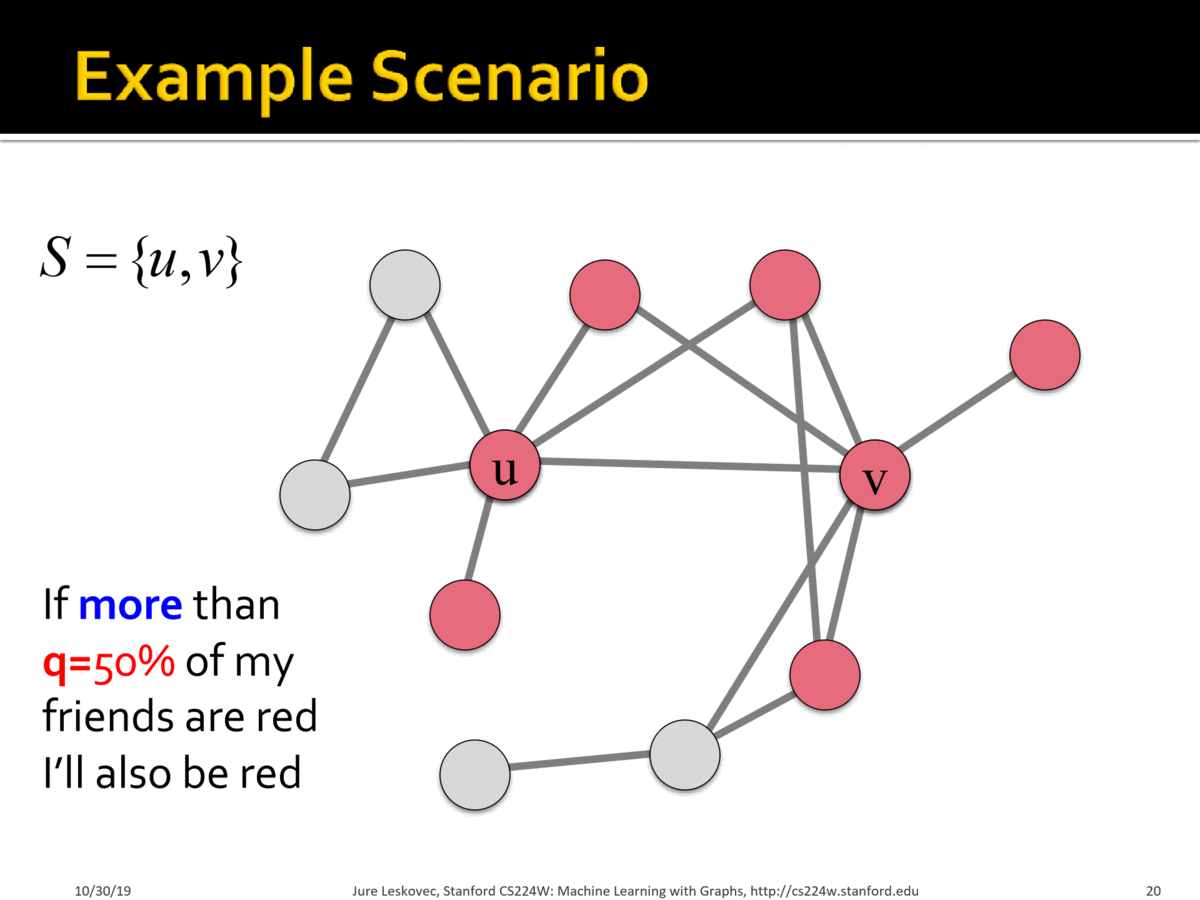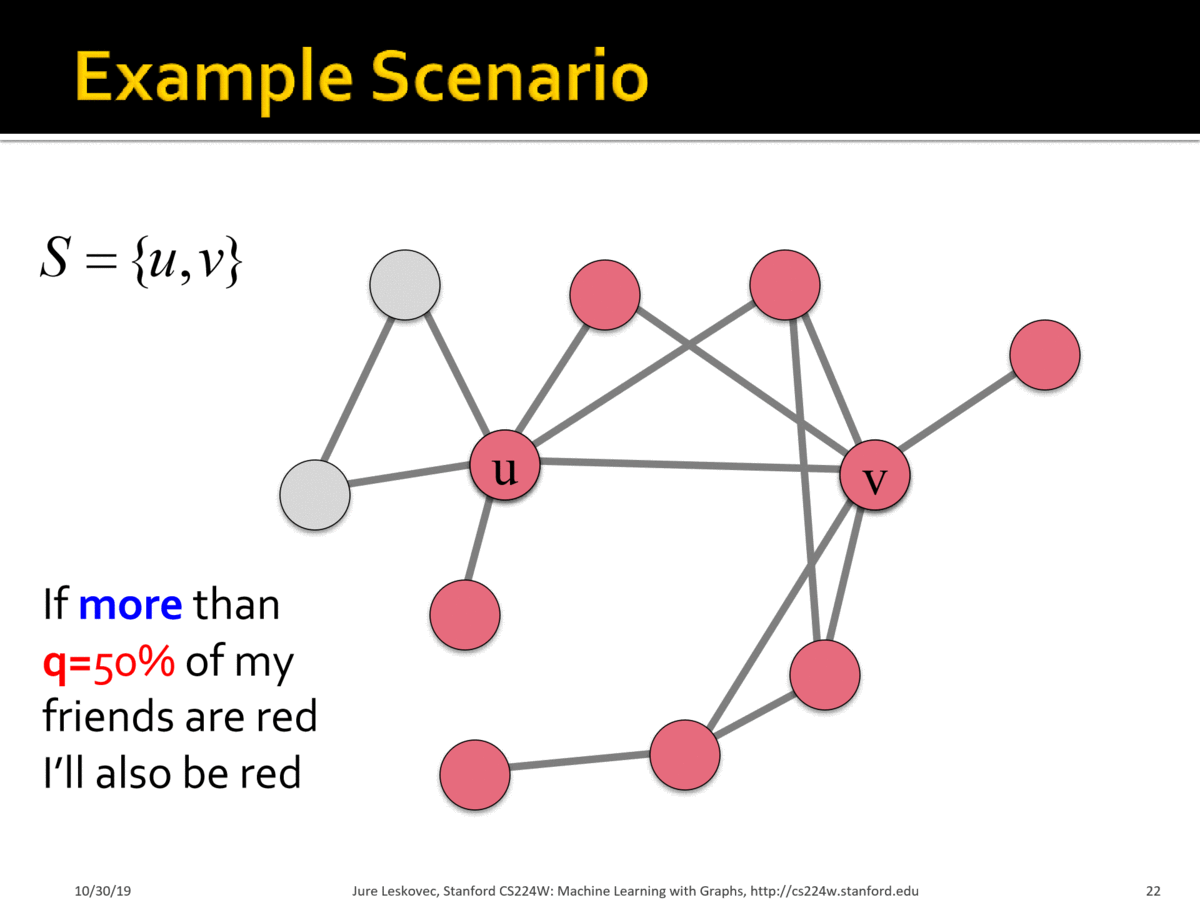
(간지나는 gif ㅎㅎ)
위의 그림을 보면, neighborhood node 의 선택에 따라 선택이 바뀌어 가는 과정을 볼 수 있다 ~
옆 사람을 보고 많이 선택을 한 방향으로 나도 선택을 했을 뿐인데, A 가 점점 전파되는 양상을 볼 수 있다 ~

Application

강의에서는 스페인 긴축방지 시위를 예시로 Cascading 의 사례를 들고 있다
Twitter 의 #hashtags 를 통해 시위 전파 양상을 살펴보았다

전파의 양상을 살펴보기 위해서는, Threshold 를 설정해 판단한다!
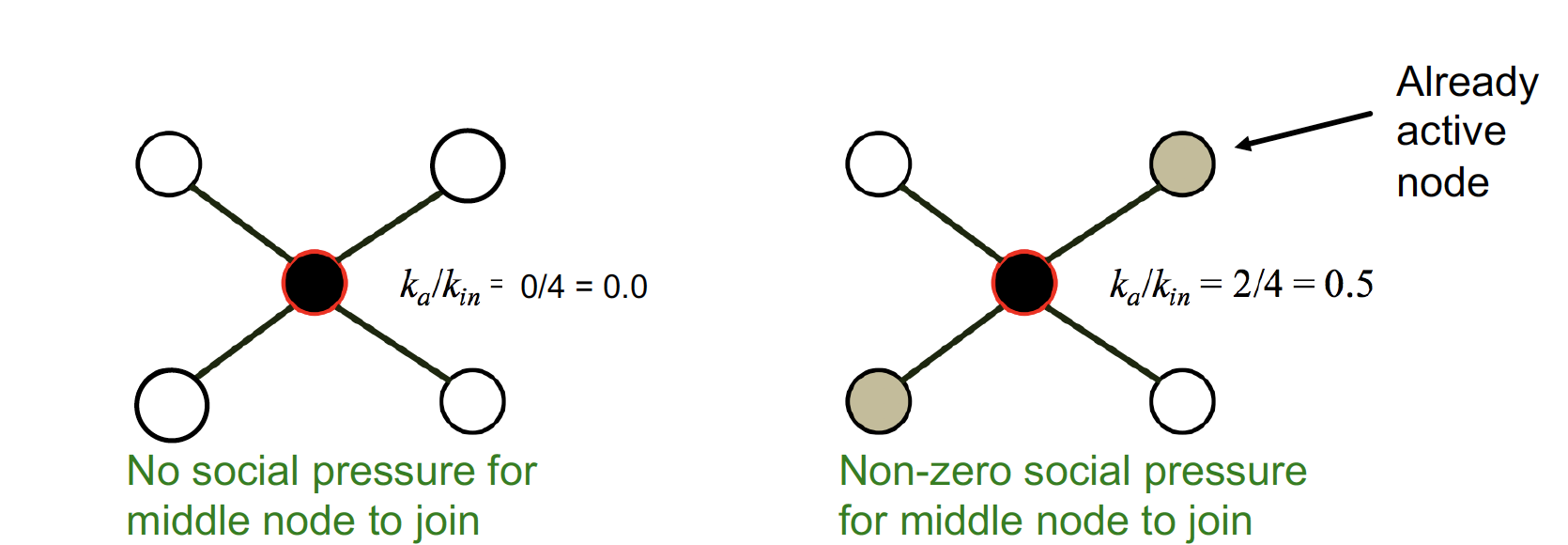
Activation Threshold = $k_{a}$ / $k_{in}$ 를 기준으로, 사회 현상을 판단했다

$k_{in}$ : user 가 active 를 시작할 때 모든 이웃의 수
$k_{a}$ : user 가 active 를 시작할 때 active 한 이웃의 수
$k_{a}$ / $k_{in} \approx 0$ : no social pressure
(참여하는 이웃이 없는데, 나 혼자 참여하는 중)
$k_{a}$ / $k_{in} \approx 1$ : high social pressure
(모두 참여한 후에 내가 참여!)

k-core decomposition

Information Cascades

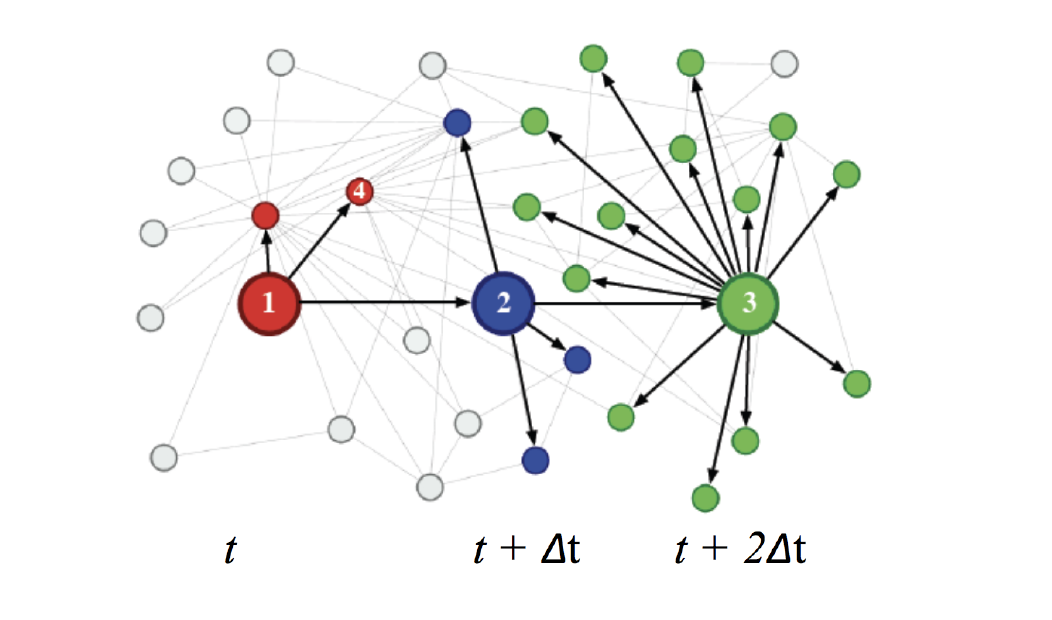
Twitter user 가 time $t$ 시점에 message 를 남겼을 때, ( $t$ , $t + \Delta t$ ) 사이에 follwer 가 message 를 남긴다면, cascading 이 조성되었다고 할 수 있다!

그렇지만 모든 cascade 가 성공하는 것은 아닌데 ...

Who starts the Successful Cascades?

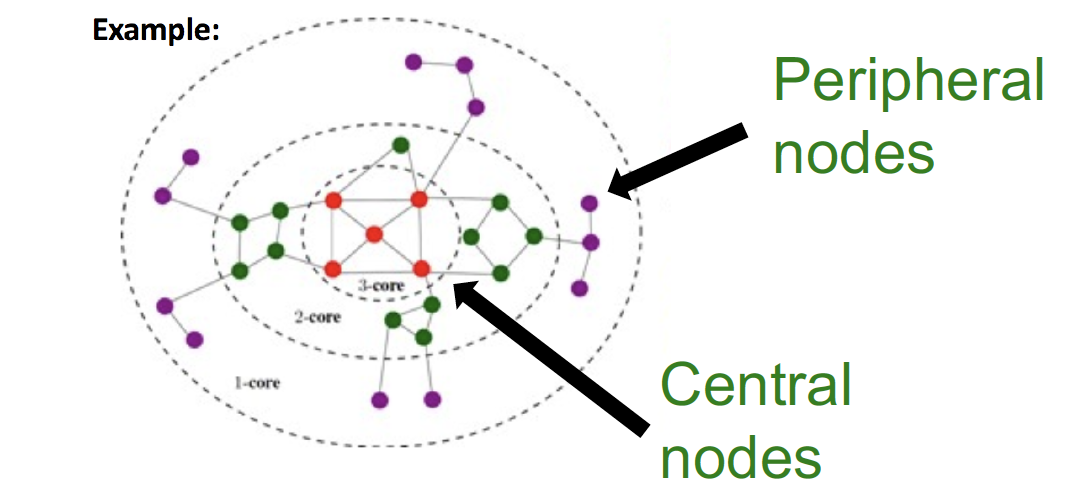
k-core decomposition 을 통해 graph 를 분해하고,
central 한 node 일 수록 (k 값이 클 수록) cascade에 성공할 가능성이 높은 node 라고 판단한다!

✔︎ k-core graph
그래프에 있는 모든 node 가 k 개 (이상)의 edge 를 갖는다는 것을 의미!

처음에 설명만 듣고, 모든 node 가 k 개의 degree 를 가지고 있는 subgraph 로 나눈 건가 ~? 라고 생각했는데... 단순히 생각했을 때 어긋나는 부분들이 있어서 찾아보니... 찾는 방법이 있다고 한다

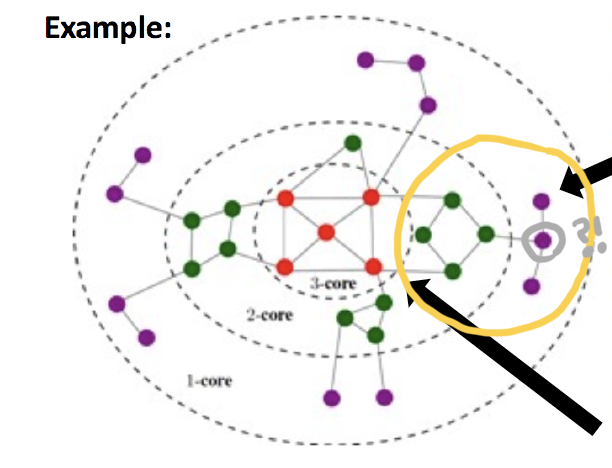
위의 예시에서, 그림만 보고 회색 부분 degree=2 인데 왜 2-core 가 아닐까... 생각했는데,

graph G 에서 k-core 를 찾기 위해서는, 다음과 같은 순서를 거친다고 한다
1. G의 모든 노드 v에 대하여 만약 v가 k개 이하의 edge를 가지면 v를 제거한다.
2. 만약 1단계에서 제거된 노드가 없으면 k-core를 찾은 것이다. 만약 1단계에서 제거된 노드가 있으면 1단계로 간다. 만약 모든 노드가 제거되었으면 k-core가 없는 것으므로 끝낸다.

따라서 위의 동일 예시에 대해, 2-core 를 찾는 과정을 그림으로 살펴보면 ~

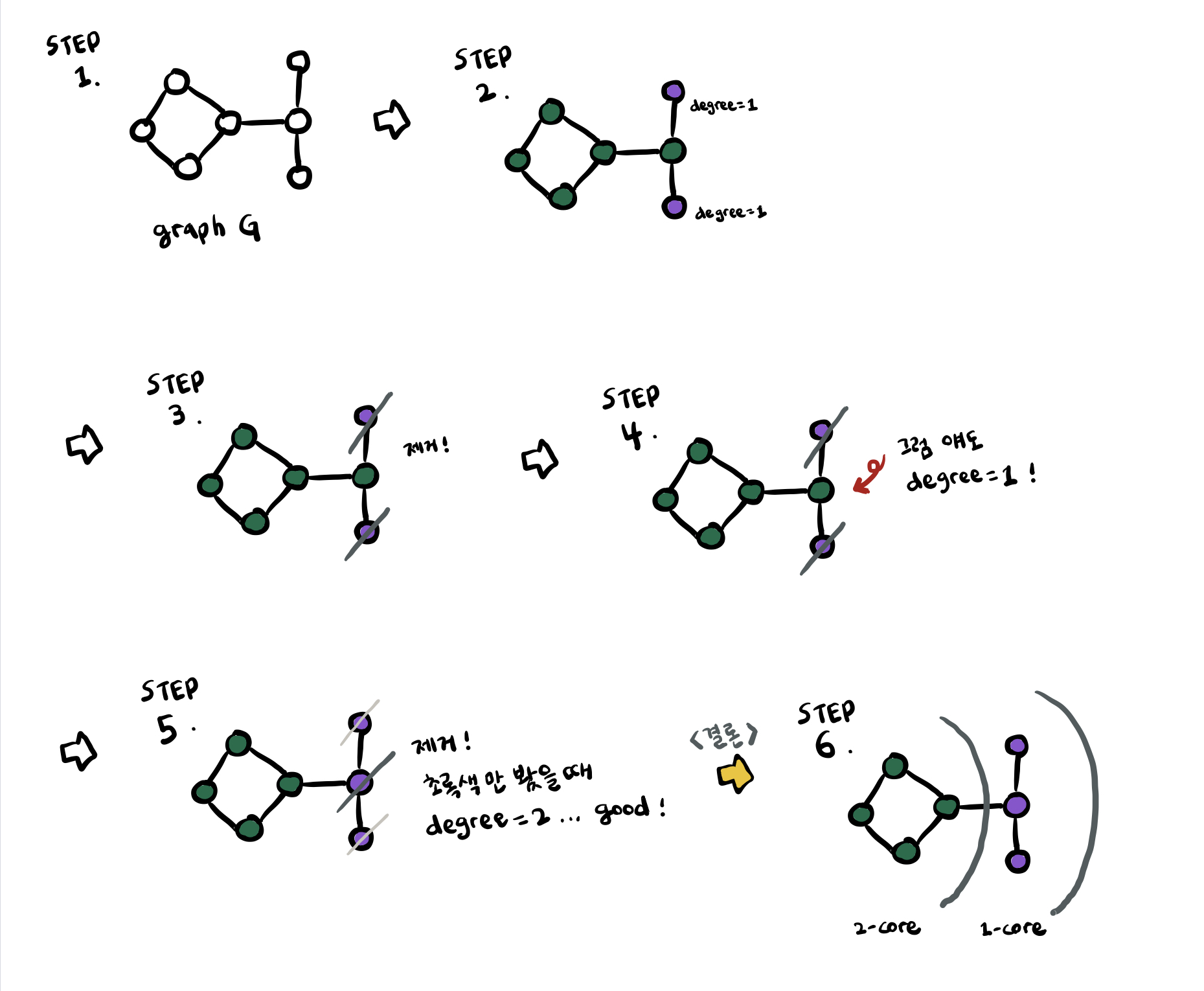
이렇게 된다구 함 ... ㅎㅅㅎ
결론 : k 보다 작은 차수를 가진 node 를 반복적으로 제거해 나가면서, k-core graph 를 찾는다

높은 차수를 갖는 k-core graph 를 찾으면, 해당 graph 에 속하는 node 가 central node 임을 의미하고, 이러한 node 가 cascade 를 잘 할 가능성이 높은 node 라고 한다 ~

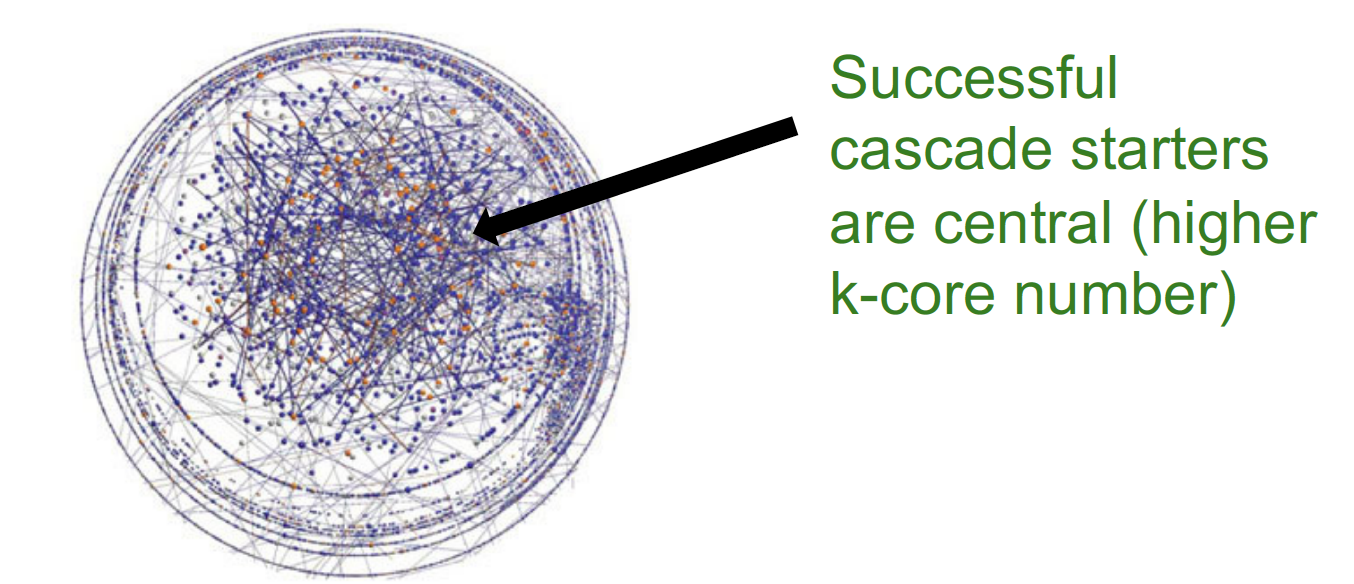
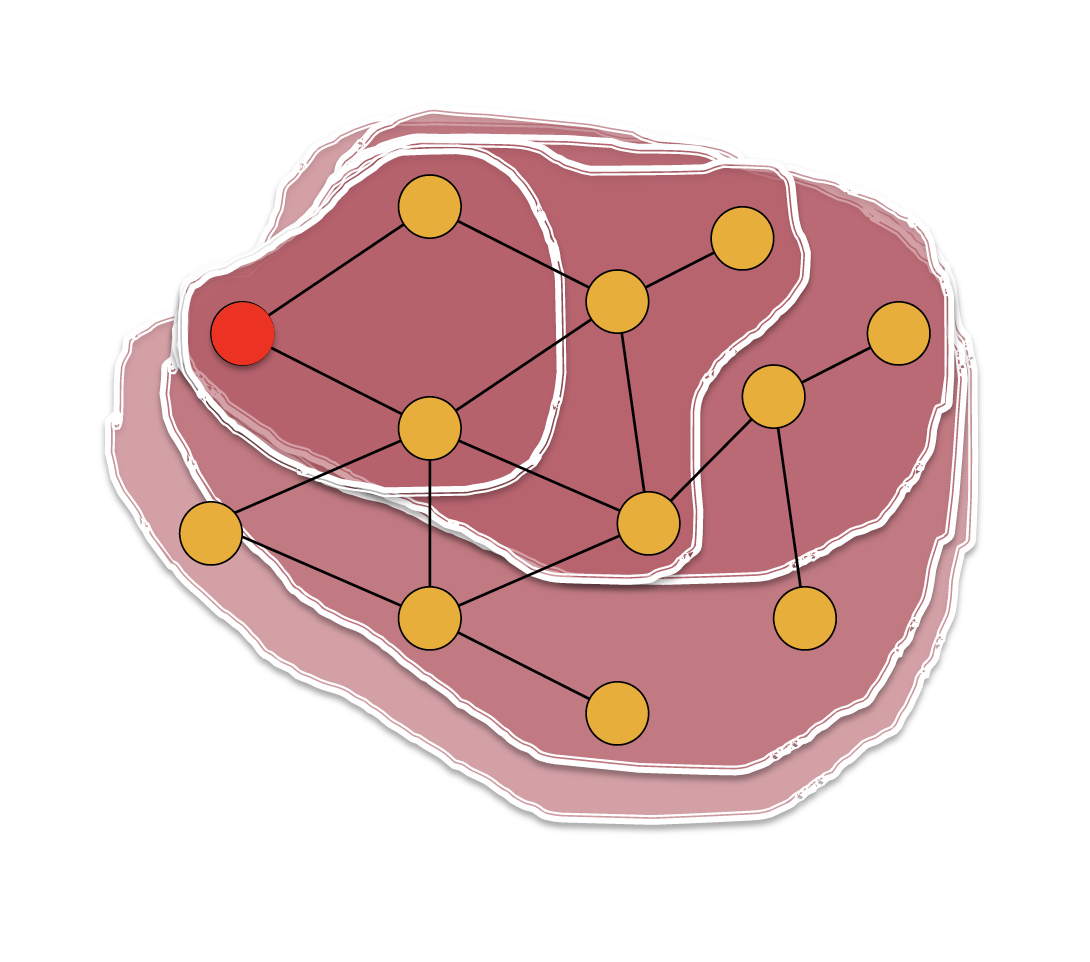
위의 그림에서 빨간색 node 가 higher k-core value 를 갖는 node 이다
이러한 node 들이 start 해야 cascade 가 성공할 가능성이 높다고 한다

2. Extending the Model : Allow People to Adopt A and B

지금까지 A or B 만 선택하는 diffusion model 을 봤는데,
A 혹은 B 라는 두 가지 선택만을 고려하지 않고, A와 B 모두 선택할 수 있는 AB 선택지를 추가해 보자 ~

Extending the Model

A vs B 에서는, 위와 동일하게 payoff 를 얻는다

A-A : a
B-B : b
A-B : 0

여기에 하나의 player 가 A와 B를 모두를 선택하는 extra strategy 를 추가한다!
이 경우 얻는 payoff 는 다음과 같다

AB-A : a
AB-B : b
AB-AB : max(a,b)
단, AB 선택 시 cost c 를 지불한다

Cascades & Compatibility : Model

그럼 이러한 상황에서 A 가 (or AB) 어떻게 전파될까 ~

모든 node 는 infinite network 에 있고, B에서 시작한다
finite set S 만 A 를 선택한다!
ex. 위의 예시와 같이, 갤럭시 러버 or 사과 농장 러버
time dependency model 이다 (t 시점의 결정은 t-1 시점의 neighborhood state 에 영향을 받는다)

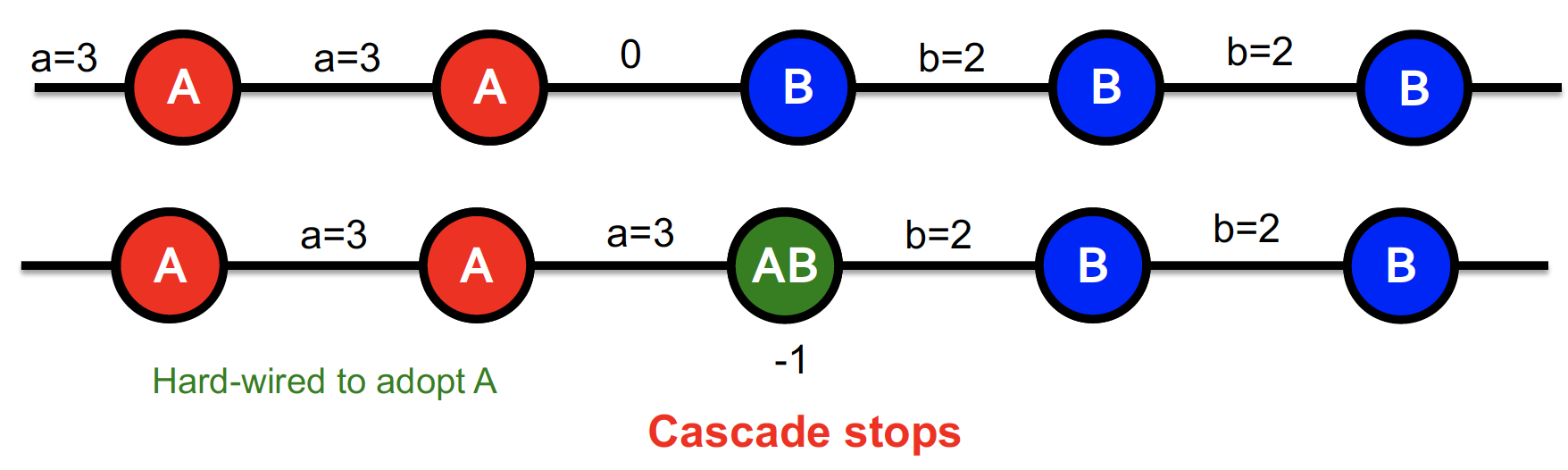
a=3, b=2, c=1 일 때, node 사이에 있는 숫자만큼 보상을 얻는다
(t-1 : 3+0+2+2=7 , t : 3+3-1+2+2=9)
따라서 가운데가 B 보다 AB 선택을 하는 것이 합리적이게 된다!
그치만 A 가 흐르는 모습은 볼 수 없다
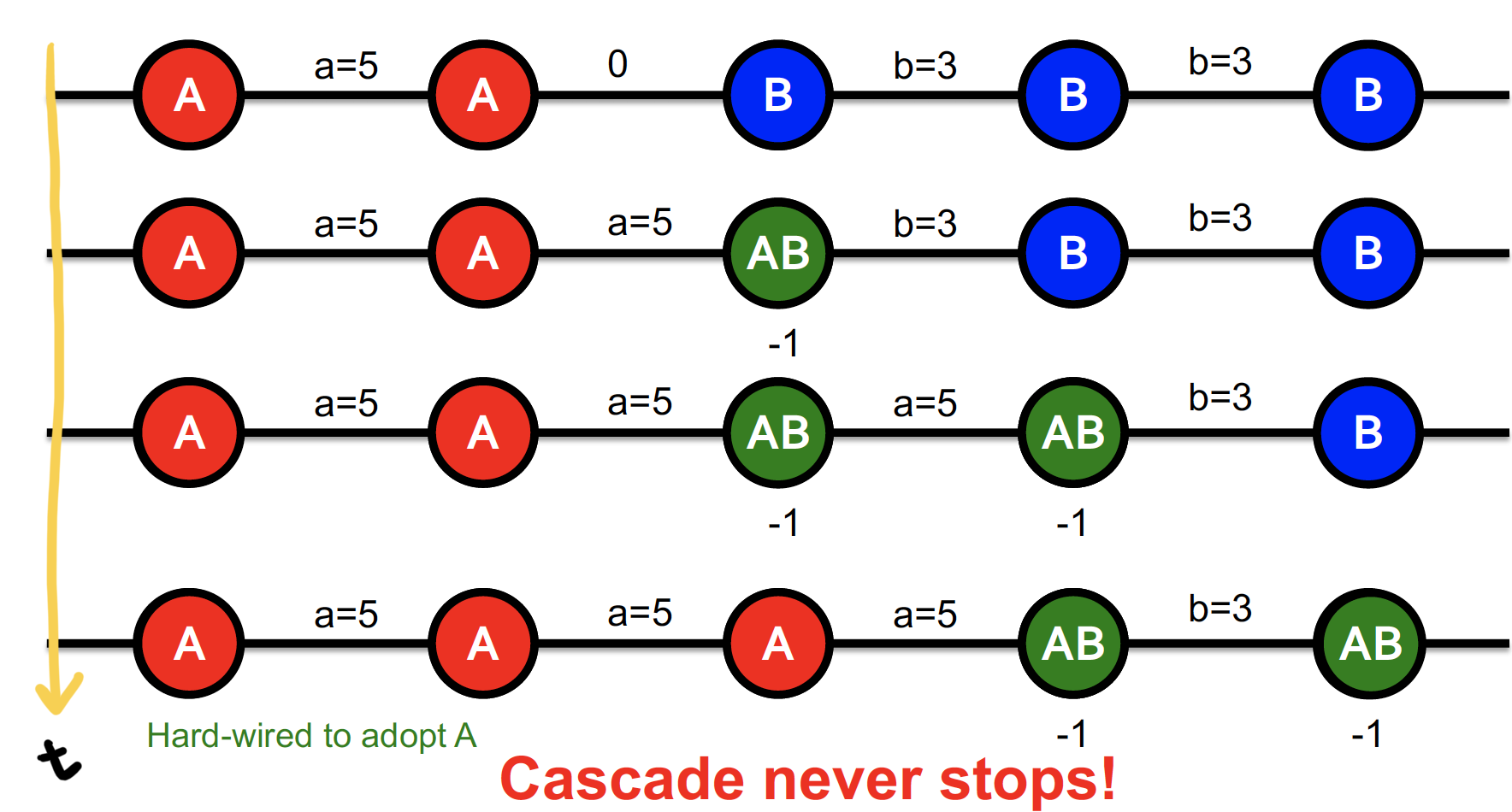
a=5, b=3, c=1 : A에 대한 보상을 늘리면 어떻게 될까 ~?
시간이 흐를수록 AB 선택으로 점점 바뀌게 되고, 이에 더하여 A로 선택이 바뀌어 감을 볼 수 있다 ~
그치만 cascade 가 끝이 나지 않을 수도 있음 ...

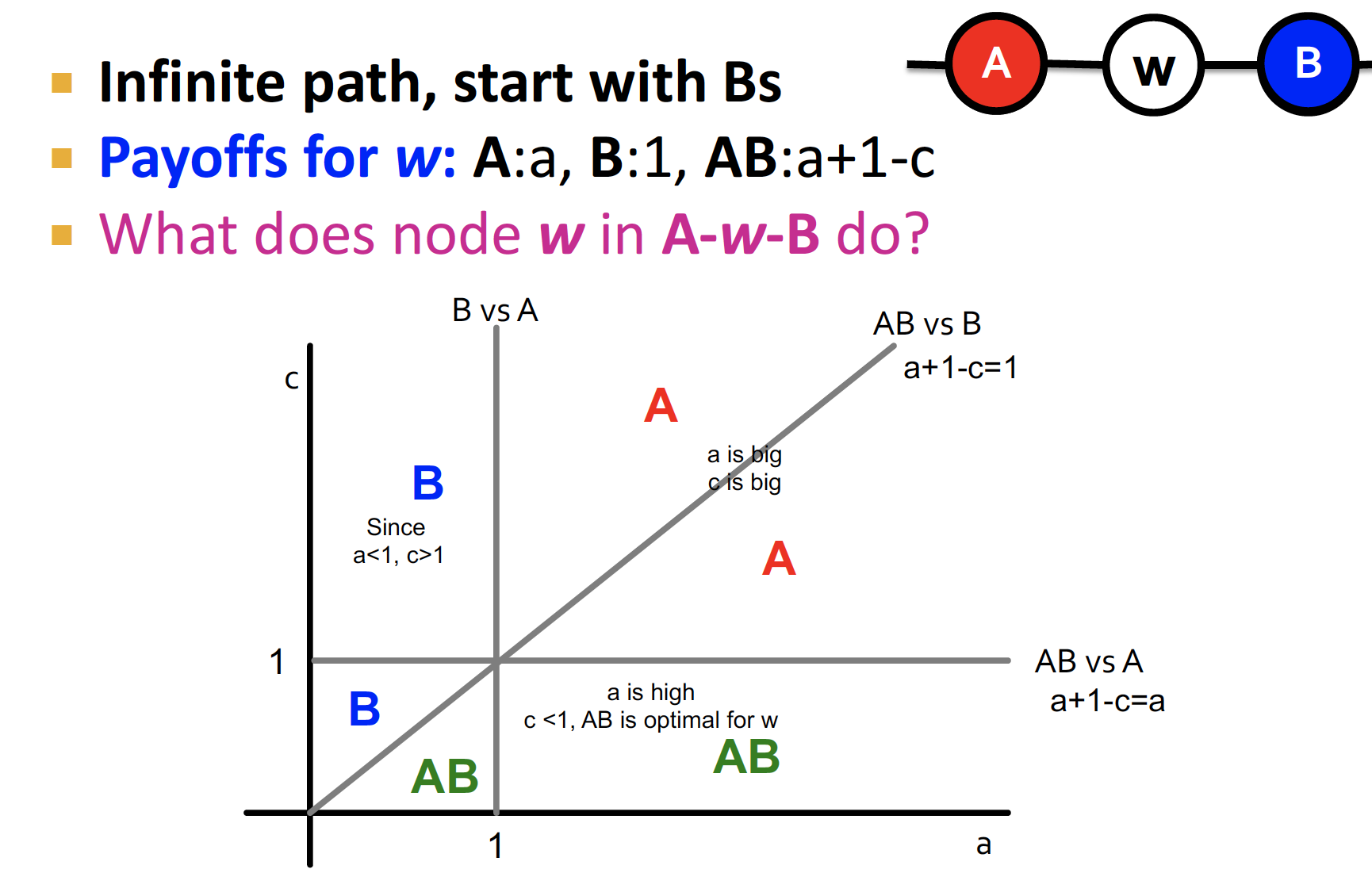
General Case

그럼 일반적인 상황에서 A 가 어떻게 전파될까 ~
모두 B를 선택한 상황에서, A가 전파되는 양상을 살펴보면 다음과 같다

A=a, B=1, AB=a+1-c 인 상황에서, 이웃에 A와 B 선택이 모두 있을 때, 나는 무엇을 선택하면 좋을까에 대한 일반적인 상황을 그래프로 나타내면 다음과 같다

A=a, B=1+1, AB=a+1-c : B 보상이 늘어난 상황

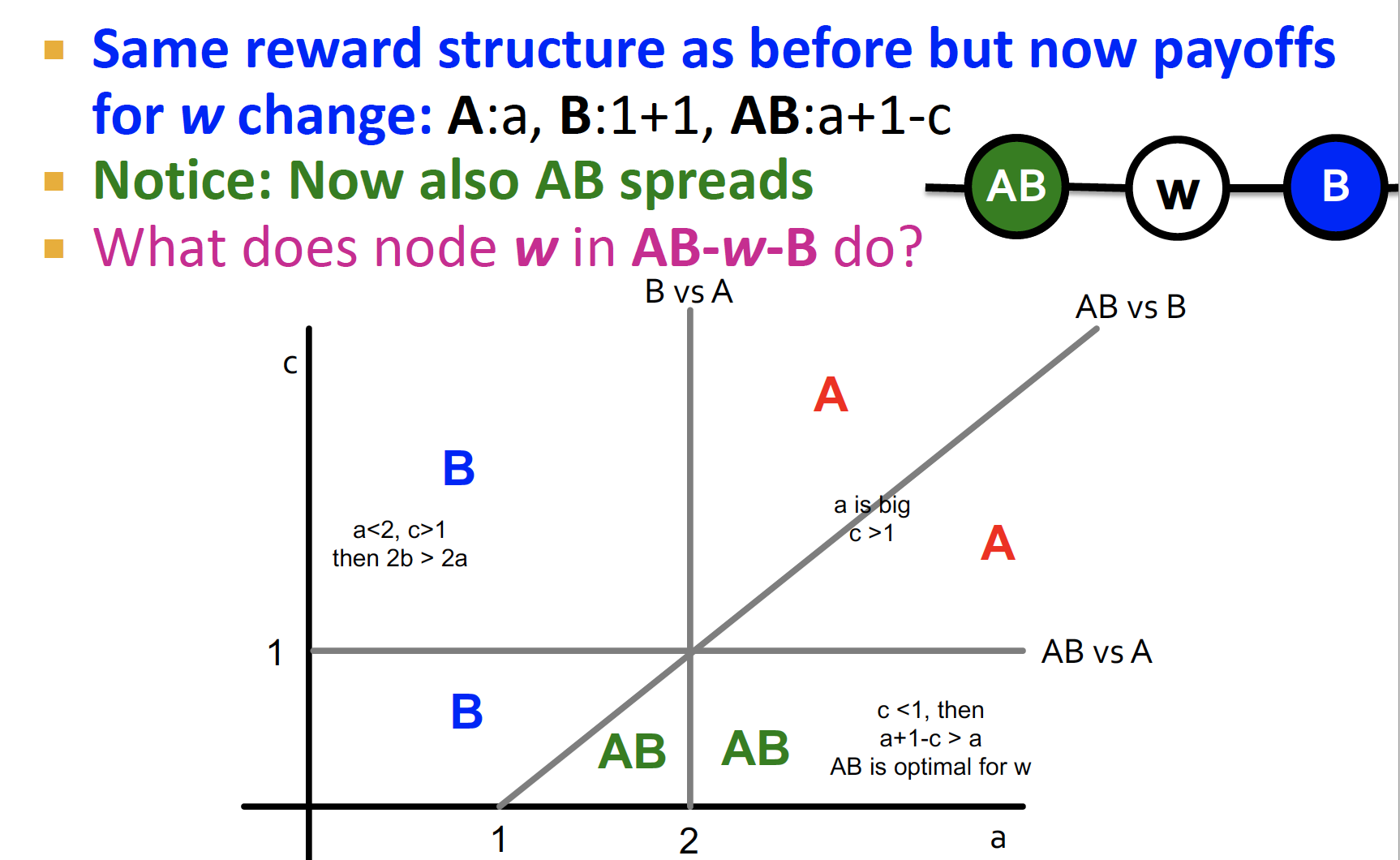
두 결과를 합치면 다음과 같다

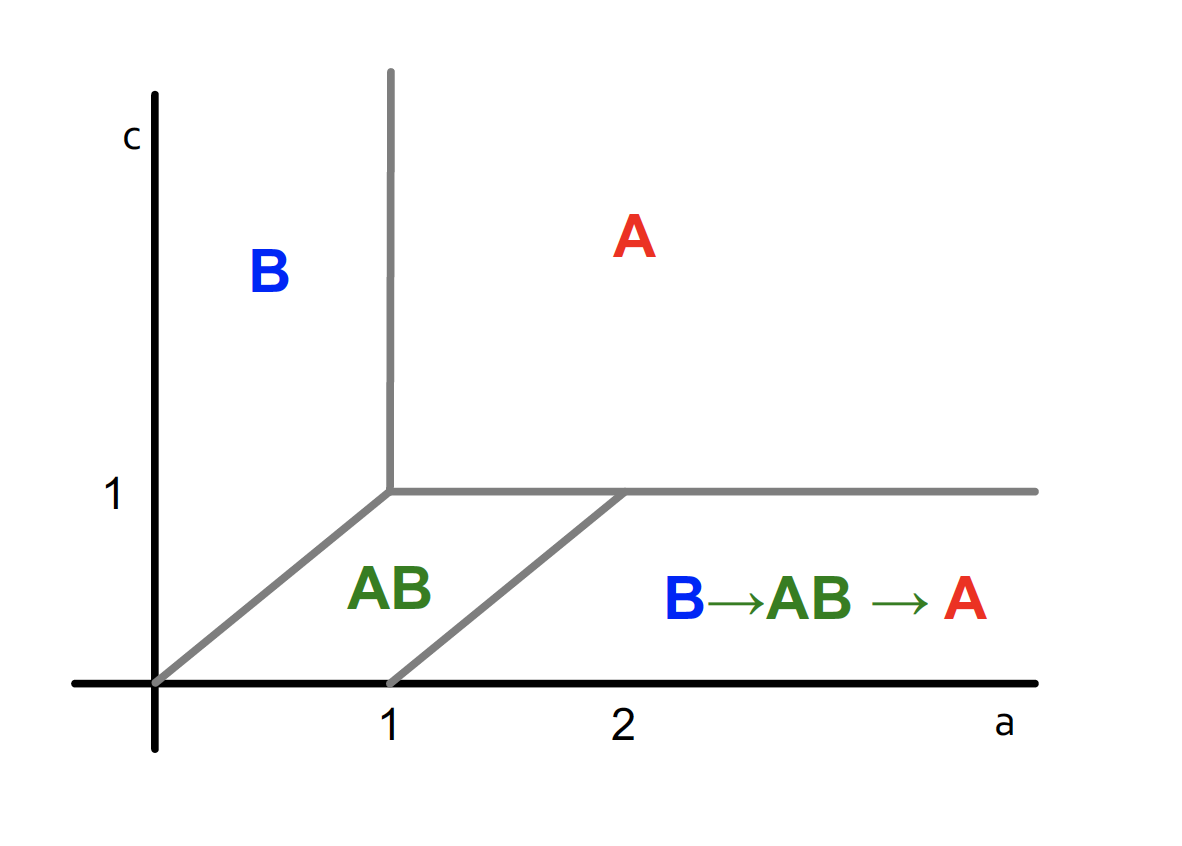
Lesson

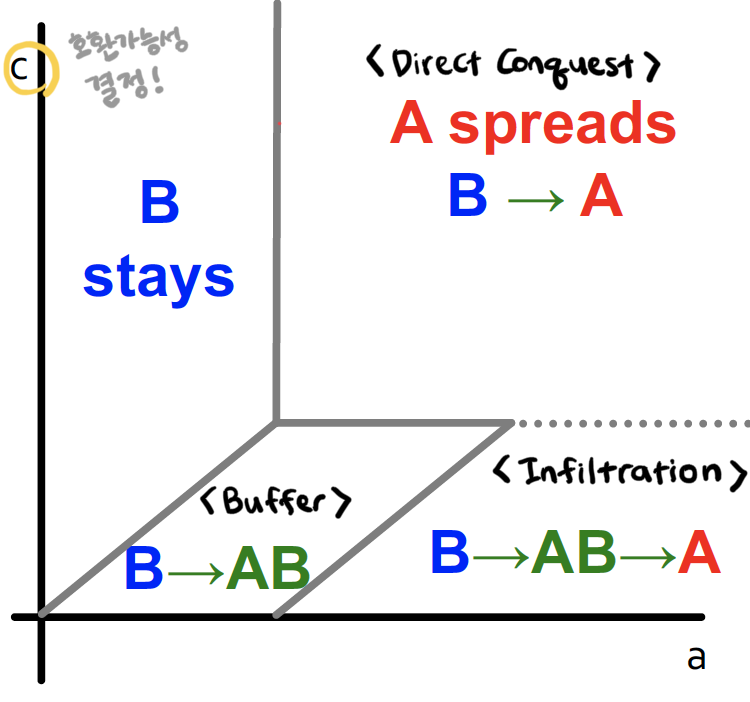
B가 default 로 있는 상황에서, A 에 대한 보상이 더 크게 설정되었을 때, 여러 상황이 존재한다
1. Infiltration : B가 호환가능성이 높다면, 사람들은 두개 다 해 보고 B를 버리게 된다
2. Direct Conquest : A가 호환가능성이 낮다면, A와 B의 경계에 있는 사람들이 선택을 하게 되고, 결국 보상이 더 큰 A를 고르게 된다
3. Buffer Zone : 최적인 상태를 고르게 되는 경우, A와 B 사이의 buffer 를 선택한다