[CS224W] 17. Reasoning over Knowledge Graphs

.·2021년 5월 18일

GNN

CS224W : GNN

목록 보기

12/12

뒤죽박죽 내맘대로 작성하는 CS224W 리뷰 ..ㅎㅅㅎ ..
들으면서 흥미로워 보였던 Knowledge Graph 에 대해 먼저 리뷰 작성해 보려구 한당

Contents

Intro to Knowledge Graph

Knowledge Graph Completion

Path Queries

Conjunctive Queries

Query2Box

1. Intro to Knowledge Graph

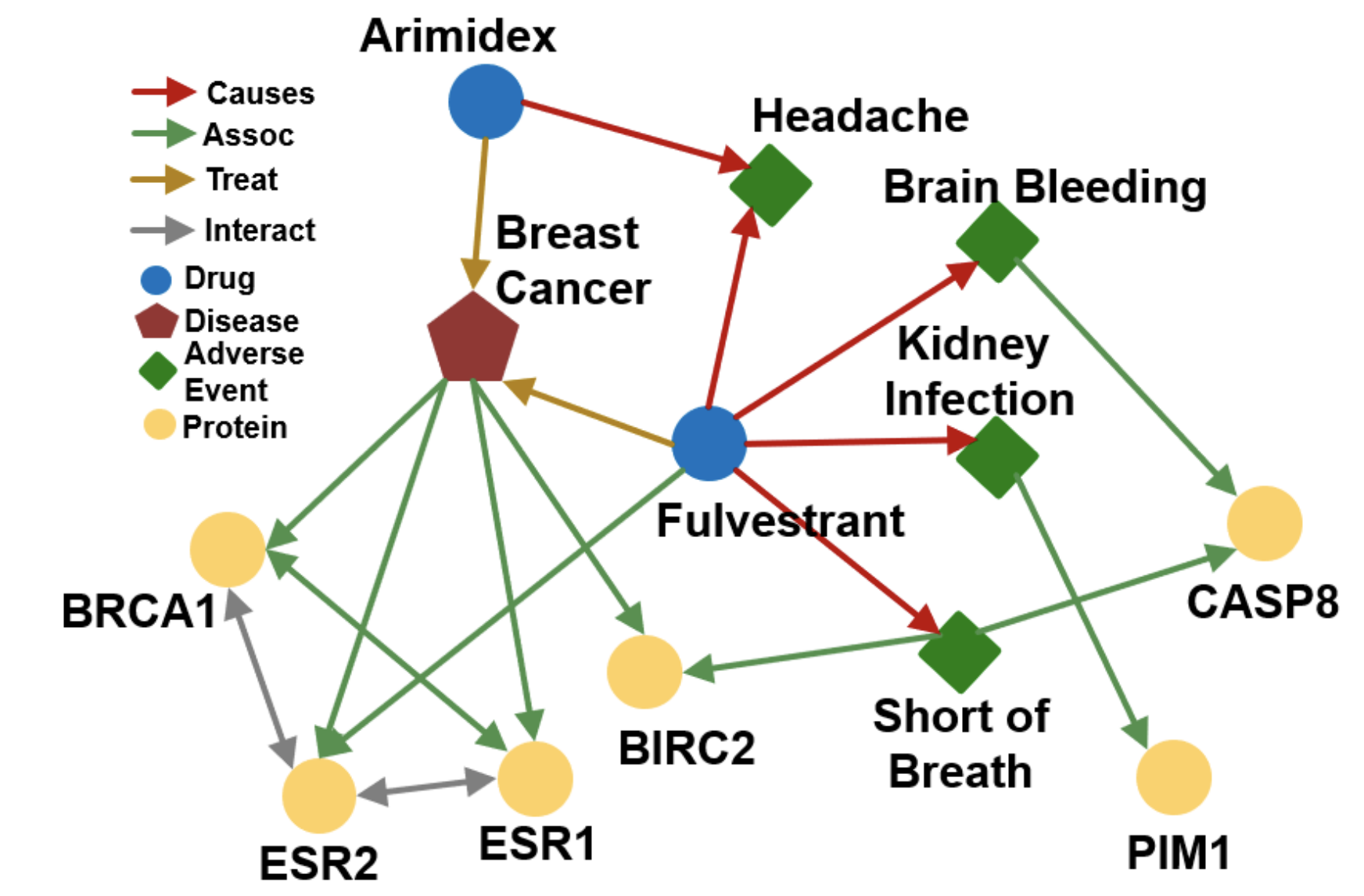
Knowledge Graph 는 말 그대로, 지식을 그래프 형태로 구축한 것을 말한다
node 가 entity 가 되며, edge 가 relationship 이 된다

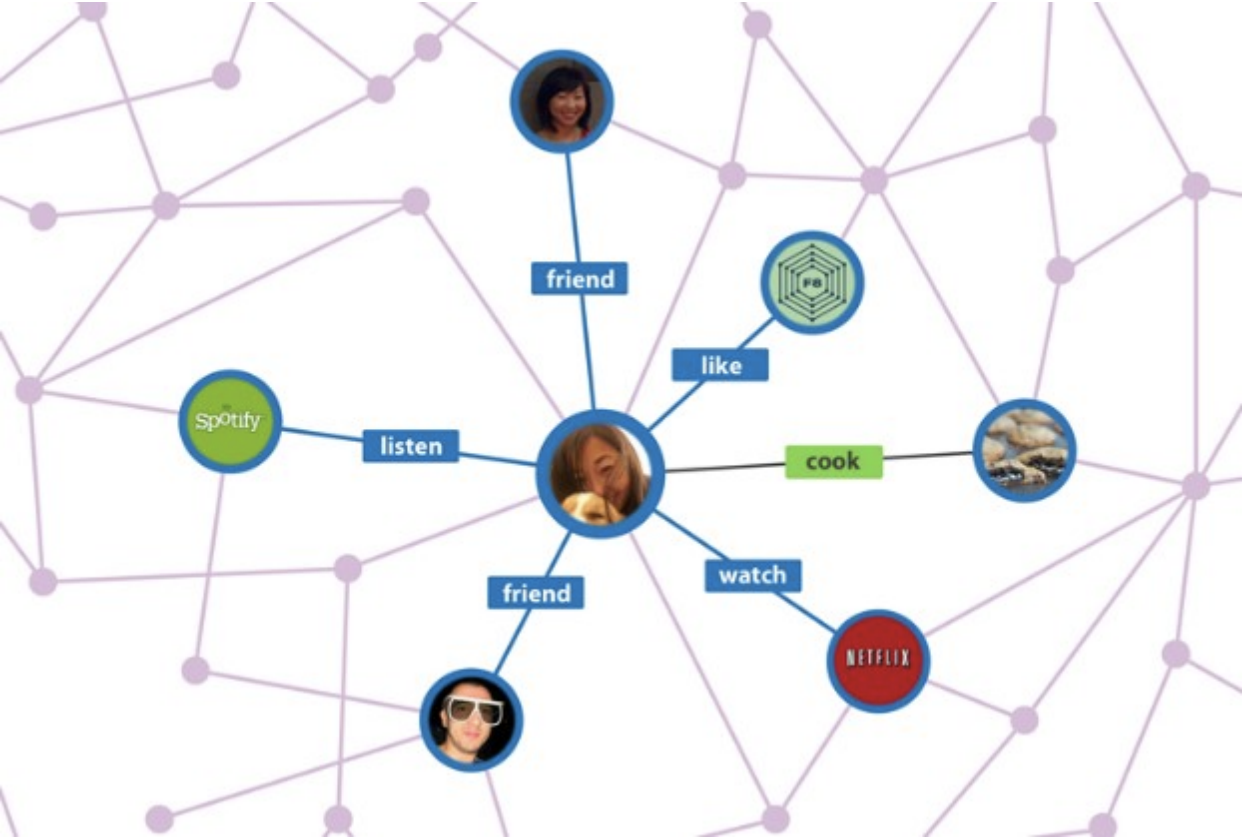
Social Network 에서,
node 는 account, song, post, feed 등의 요소가 될 수 있으며
→ 이에 상응하는 edge 는 friend, listen, watch, like 등의 요소로 구성될 수 있다

이처럼 하나의 그래프에서, node (entity) 와 이에 상응하는 edge (relationship) 는 다양한 속성을 가지고 있다

우리가 지금까지 배웠던 GNN (GCN) 은, node 와 edge 의 속성이 다양하지 않은 상황에서, Graph Representation 하는 방법론이다!
즉, node (+ node feature) 와 node 사이 연결 여부를 나타내는 (= 하나의 속성) edge 를 통해 node embedding 함으로써 그래프를 표현한다

KG 에서의 Entity 와 Relationship 은 매우 다양하므로, 일반적인 방법론을 적용해 그래프를 나타내기에는 한계가 있다
따라서 이러한 지식 그래프의 복잡성을 잘 나타내 주는 방법론에 대해 공부하게 된다 ~

Applications

Knowledge Graph 는 Information Serving, Question Answering 등 다양한 분야에 적용이 가능하다

특히 Knowledge Graph 로 구글링 했을 때, 가장 먼저 나오는 예시가 Google Knowledge Graph 인데 ...

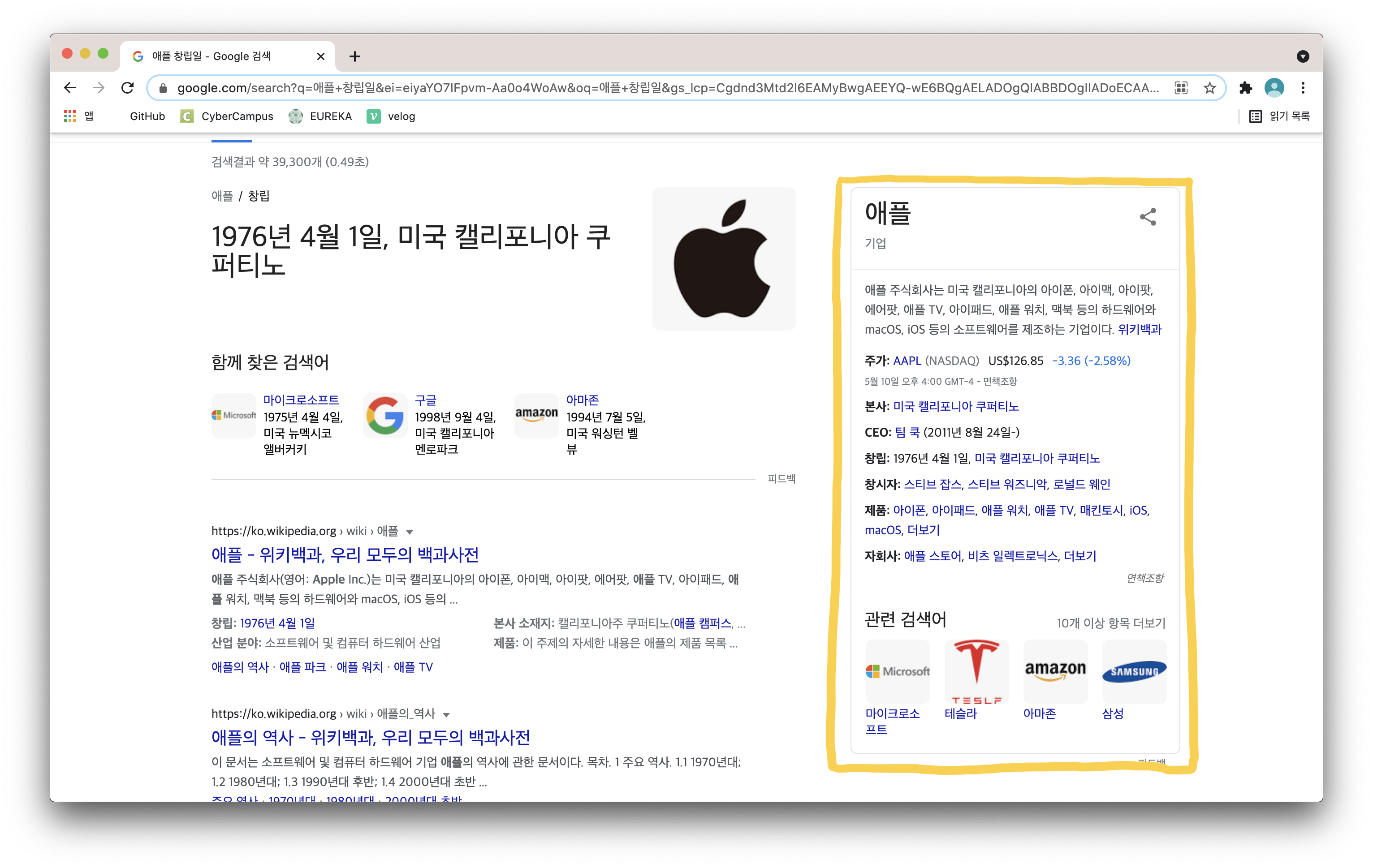
오른쪽 노란색 네모 박스가 구글의 지식그래프 예시!
애플 창립일을 검색했는데, 바로 답변이 나오고 (QA) + 애플에 대한 정보가 쭉쭉 나오고 + 관련 검색어 등이 한번에 나오는 것을 볼 수 있다
이처럼 검색했을 때, 여러 정보를 한번에 제공해 주는 것이 구글의 지식그래프 서비스 라고 한다 ~

구글은 2012년부터 이런 지식그래프 서비스를 제공해왔다고 한다
(우리나라 구글에는 2013년에 도입되었다고 한다)

2. Knowledge Graph Completion

KG 에서의 edge 는 triplet 형태로 표현 가능하다!
(𝒉, 𝙧, 𝒕) = 𝒉 (head entity), 𝙧 (relation), 𝒕 (tail entity)

embedding/vector space $\mathbb R^d$ 로 표현하기를 원하며,
true triplet (𝒉, 𝙧, 𝒕) 에 대해 = (𝒉, 𝙧) embedding 이 𝒕 embedding 과 ✨ 최대한 가깝게 ✨ 위치되는 것을 목표로 한다 ~!

그럼 여기서,
(𝒉, 𝙧) 을 어떻게 embedding 시킬 것이며 & closeness 를 어떻게 정의할 것인가 ~

Relation Patterns

embedding 방법론을 살펴보기에 앞서, 𝒉 (출발 node) 와 𝒕 (도착 node) 의 관계는 다음 세 가지로 정의할 수 있다고 한다

Symmetric Relations
- 서로간의 관계는 대칭적
- ex. 두빅스 사람들은 모두 칭구
Composition Relations
- 관계를 연산으로 표현 가능
- ex. 나와 아빠의 관계 = 나와 엄마의 관계 + 엄마와 아빠의 관계
1-to-N, N-to-1 Relations
- 하나의 entity 에 특정 연산을 거치면 여러 relationship 생성 가능
- ex. 나와 민정이 지니 등등 다른 친구들은 모두 member of 투빅스

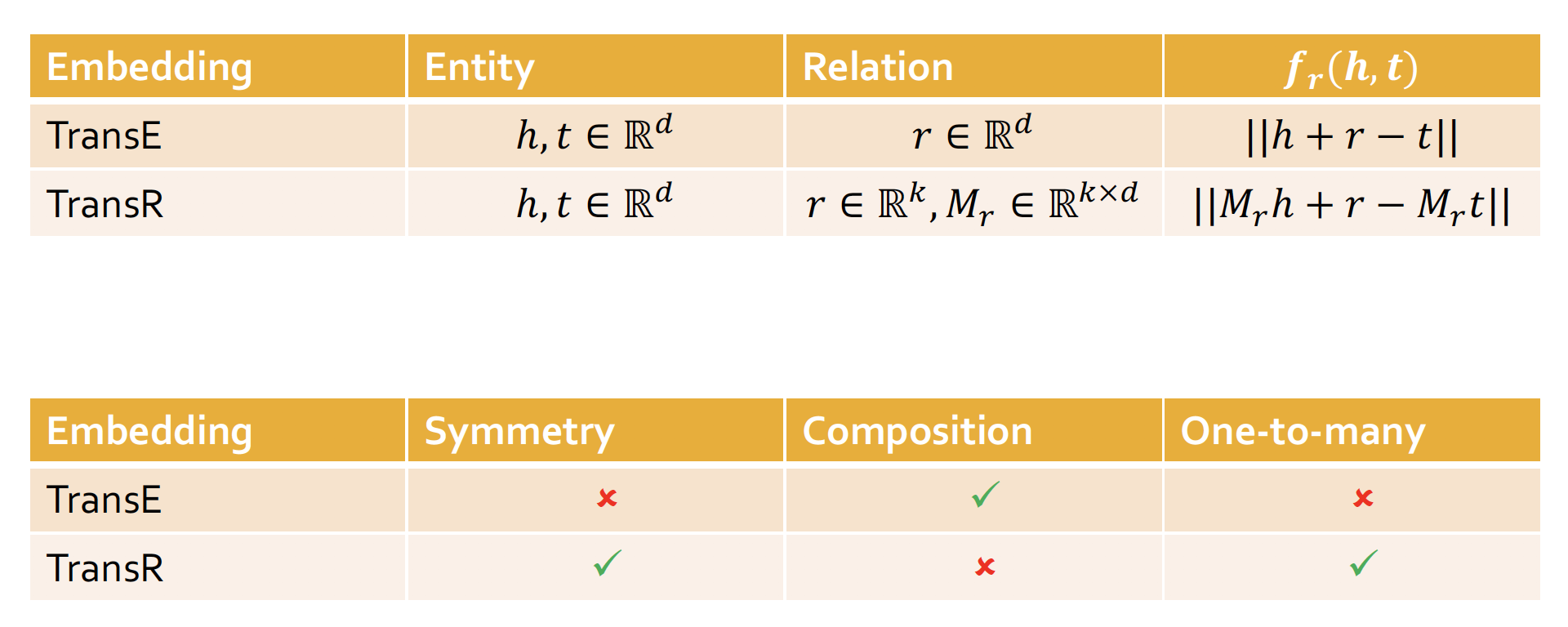
TransE

앞서 7강 : Graph Representation Learning 에서 배웠던 TransE 에 대해 다시 한번 짚고 넘어가고자 한다

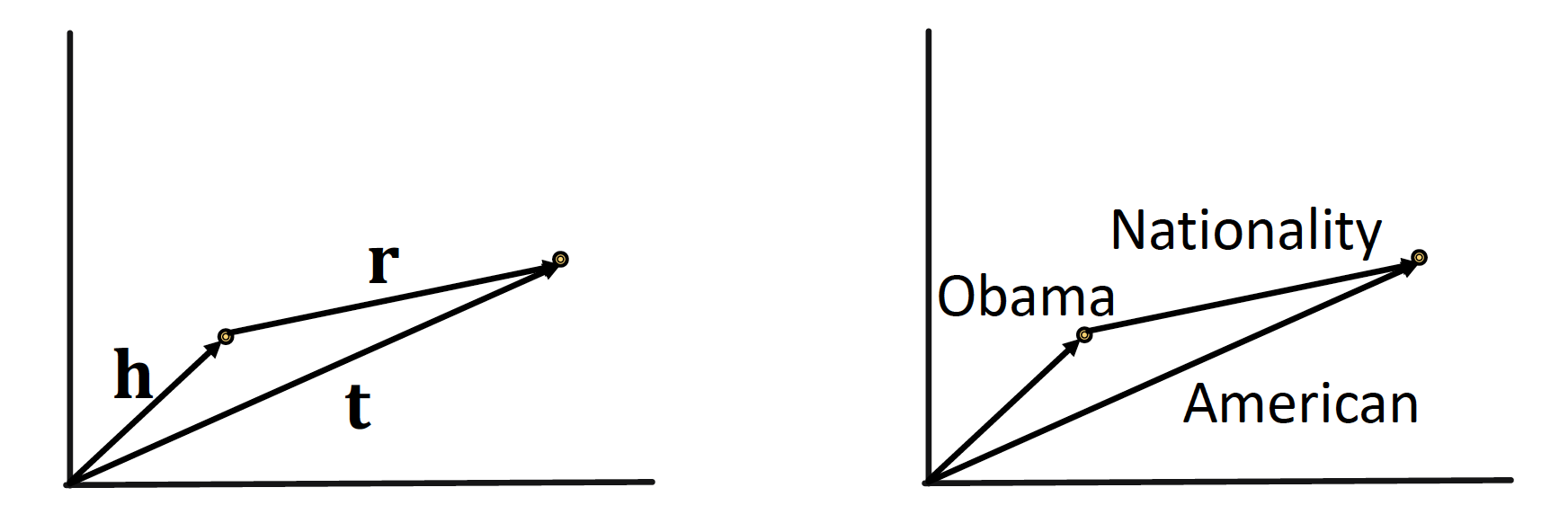
TransE는 triplet (𝒉, 𝙧, 𝒕) 를 같은 공간인 임의의 $d$ 차원으로 mapping 하는 embedding 방법론을 말한다

TransE = Relations are represented as Translations
𝒉 (head) + 𝙧 (relations) = 𝒕 (tail) 를 만족하기를 원하며,
이 때의 Score Function 은 $f_r(h,t) = ||h+r-t||$ 이다.
(= 𝒉 에서 𝙧 만큼 이동했을 때 𝒕 가 나오면 매우 매우 good good)

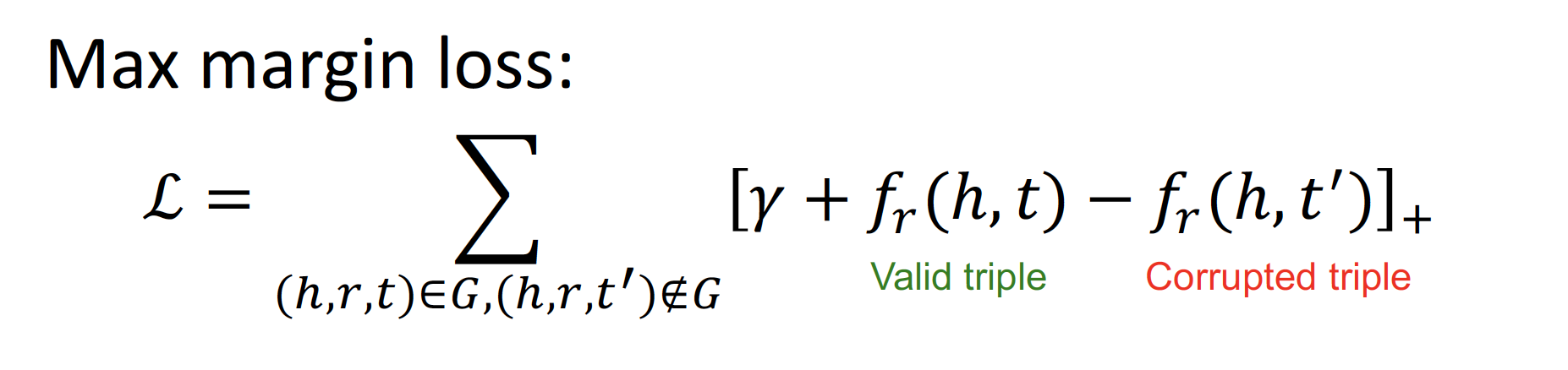
Valid triplet (positive sample) Score Function 값이 작을수록
(= 𝒉 와 𝒕 사이의 거리가 가까울수록),
Corrupted triplet (negative sample) Score Function 값이 클수록
(= 𝒉 와 𝒕 사이의 거리가 멀어질수록)
→ loss 값이 작아지게끔 margin loss $\mathcal L$ 을 설정한다

Limitations of TransE

TransE 는 Composition Relation, 즉 relationship 간의 관계를 형성함으로써 또 다른 relationship 을 표현할 수 있다는 장점이 있다!

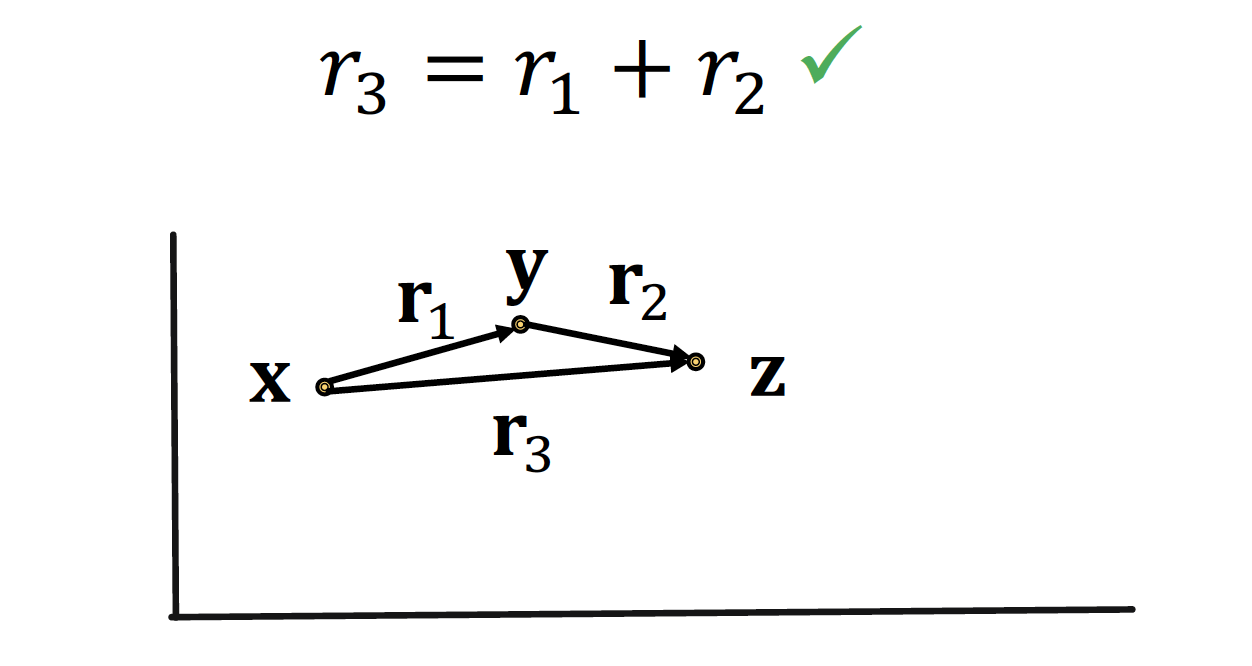
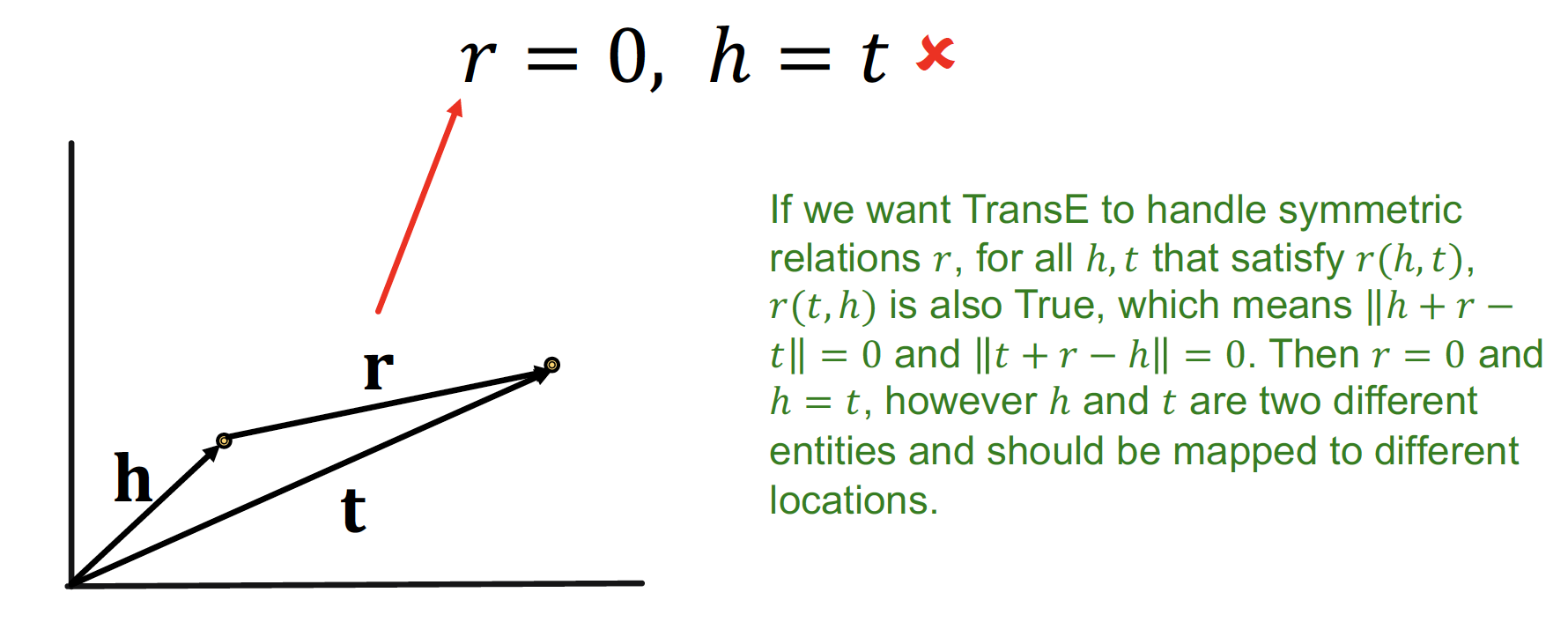
그렇지만,

Symmetric Relation 을 표현할 수 없다
𝙧 = 0 인 경우, 𝒉 = 𝒕 가 되어야 하지만, 실제로 mapping 된 것을 보면 서로 다른 벡터임을 알 수 있다

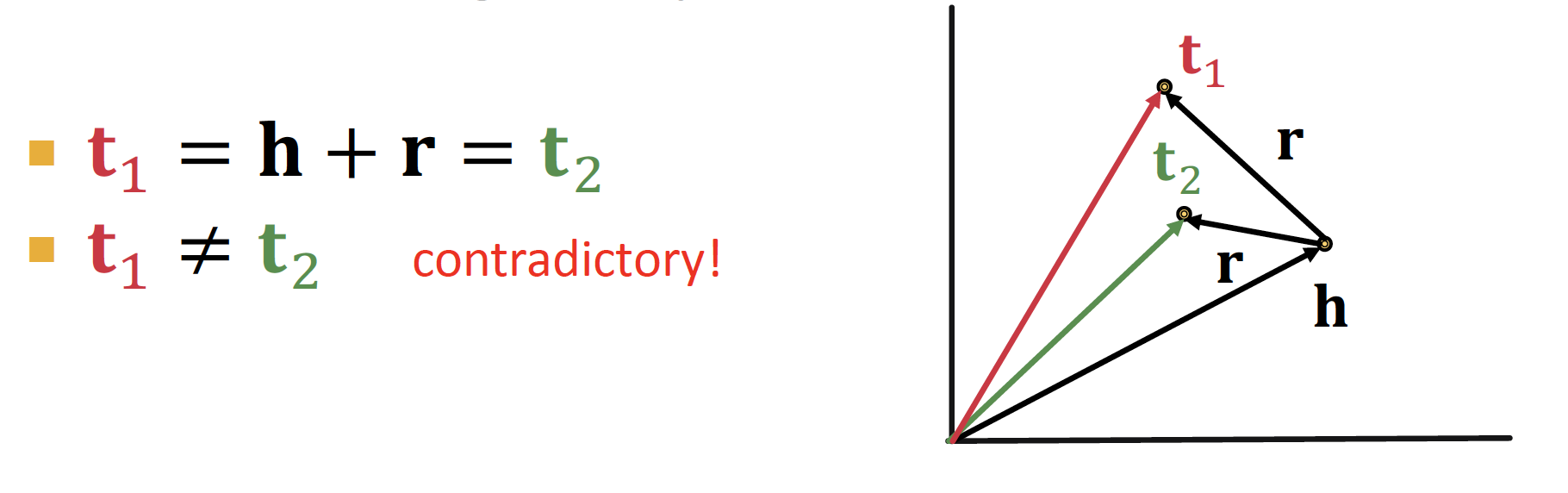
N-array Relation 을 표현할 수 없다
위의 member of 투빅스 예시처럼, 𝒉 entity 에 많은 𝙧 을 포함하고 있는 경우, TransE를 통해서는 다양한 𝒕 를 반영할 수 없다

TransR

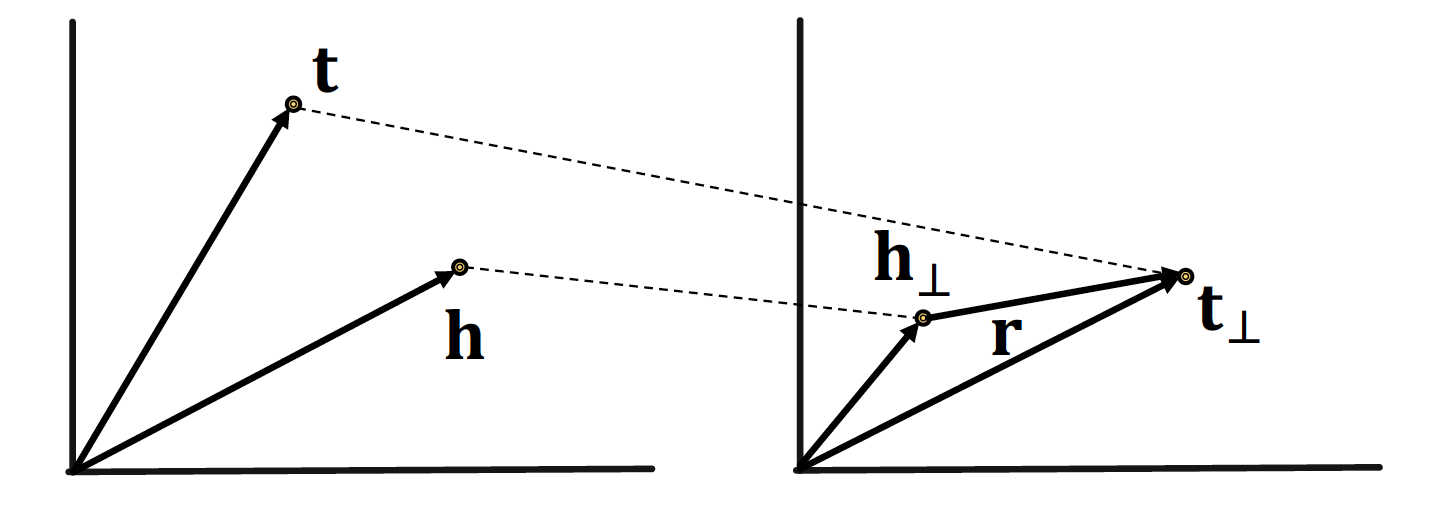
entity (𝒉, 𝒕) 와 relation (𝙧) 을 동일한 semantic space 에 두지 않고,
entity와 relation을 구분된 공간 (entity space, multiple relation spaces)에 embedding 하자는 아이디어를 적용한 것이 TransR ~

entity 는 $d$ 차원으로 mapping 하고, relation 은 vector $r$ 로써 $k$ 차원으로 mapping 한다
embedding matrix $M_r$ 의 shape 는 (k, d) 가 된다!

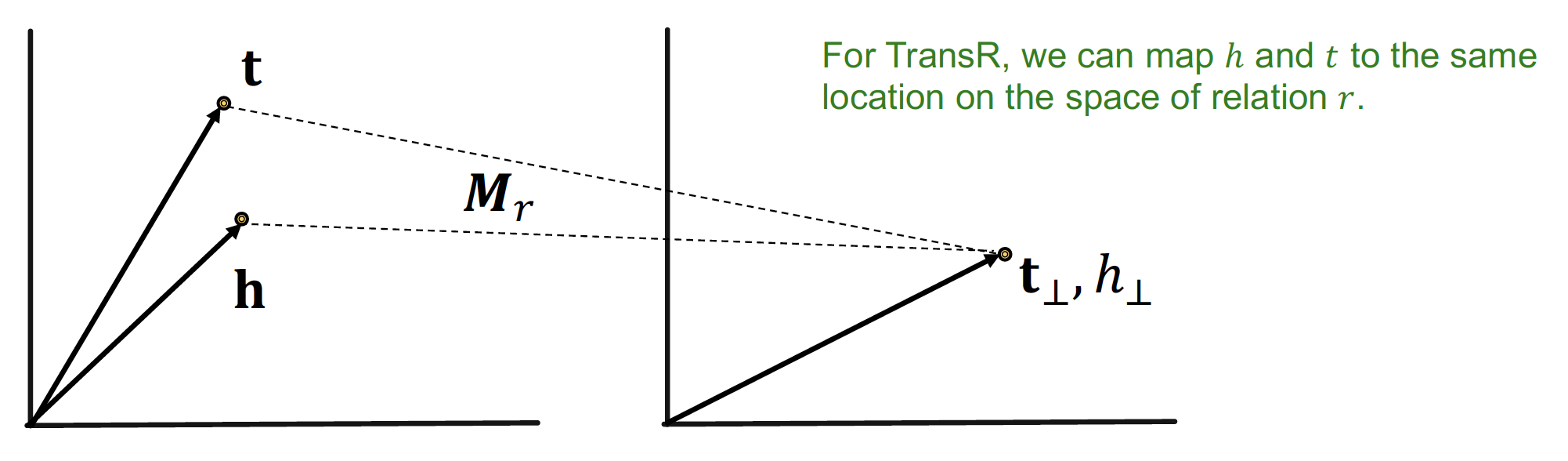
Relations in TransR

Symmetric Relation 특성을 보존할 수 있다
N-array Relation 또한 표현 가능하다
$d$ 차원에서 각각 다른 entity 더라도, $r$ 을 통해 $k$ 차원으로 mapping 시킨다면
→ 같은 값으로 embedding 될 수 있다

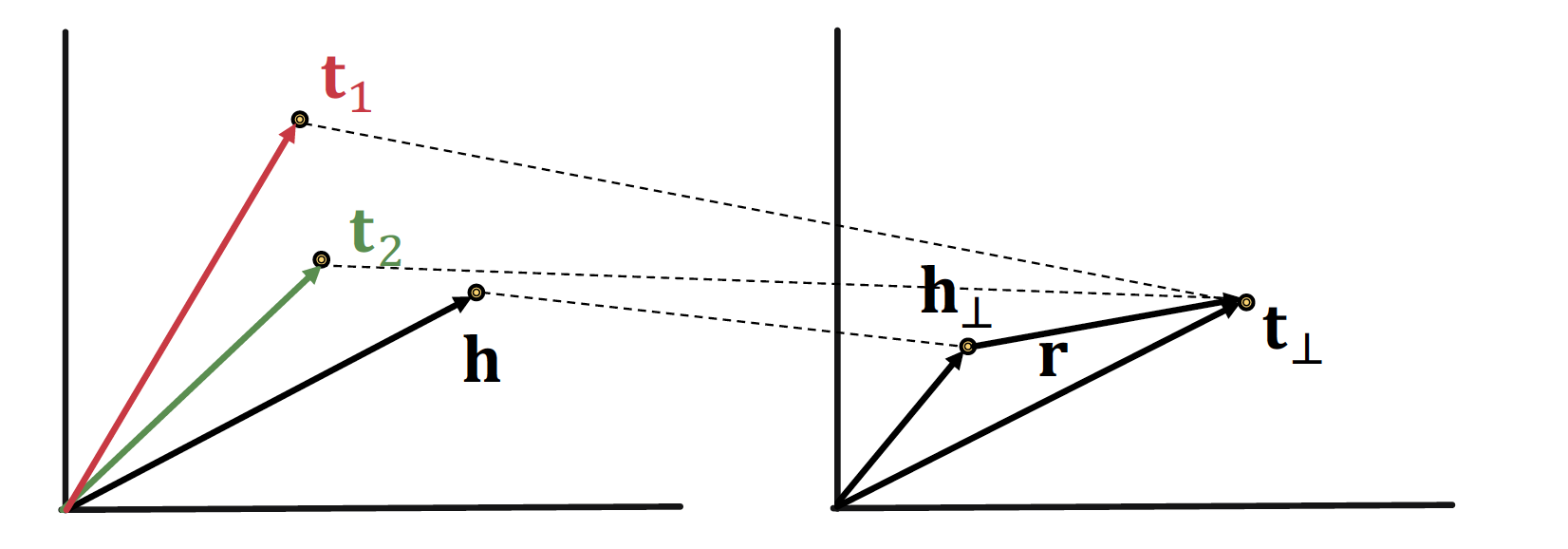
But ... Composition Relation 표현이 불가능하다
$\because$ TransR 에서 모든 $r$ 은 각자 다른 space 에 mapping 하므로!

Translation-Based Embedding

따라서 위의 관계를 한번에 표로 정리해 보면 다음과 같다 ~

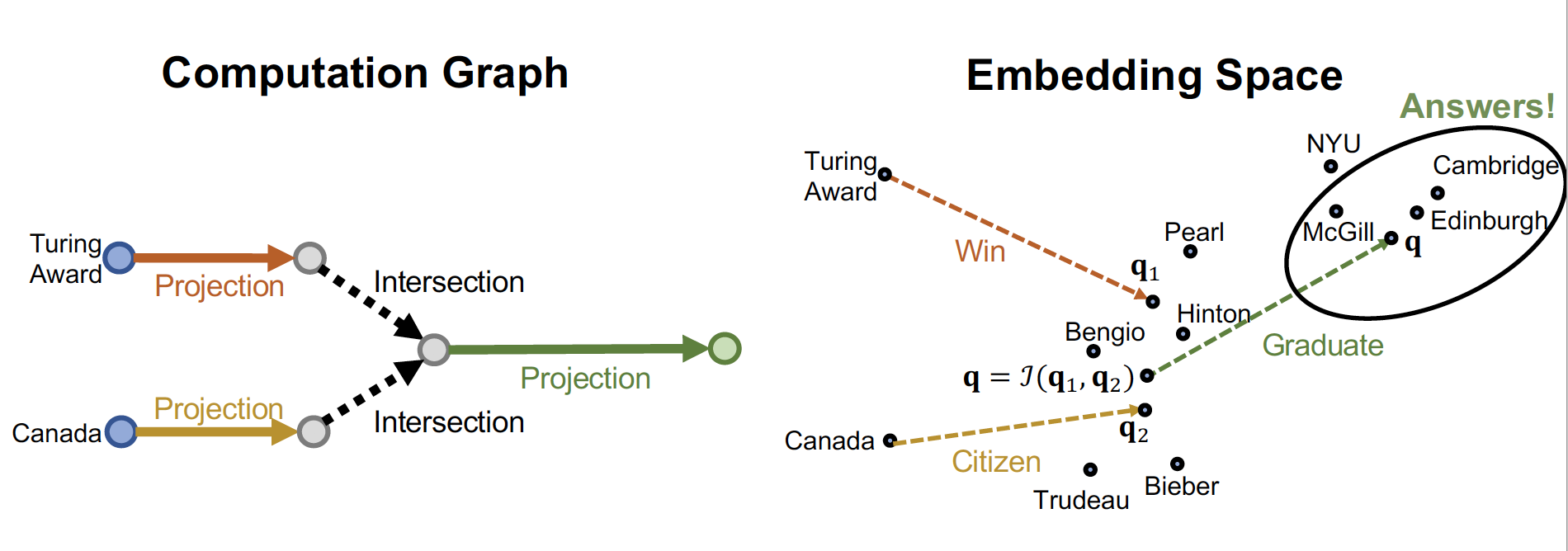
3. Path Queries

multi-hop reasoning (= 단순하게 바로 답을 구할 수 있는 질문이 아니라, 타고 타고 들어가는 질문) 을 진행한다면 어떻게 될까 ~?
incomplete massive KG 에서 복잡한 query 에 효율적으로 대답하고자 한다

Query Types on KG

Query Type 은 크게 4가지 종류가 존재한다
1. One-hop Query : 바로 답을 구할 수 있는 단순한 질문
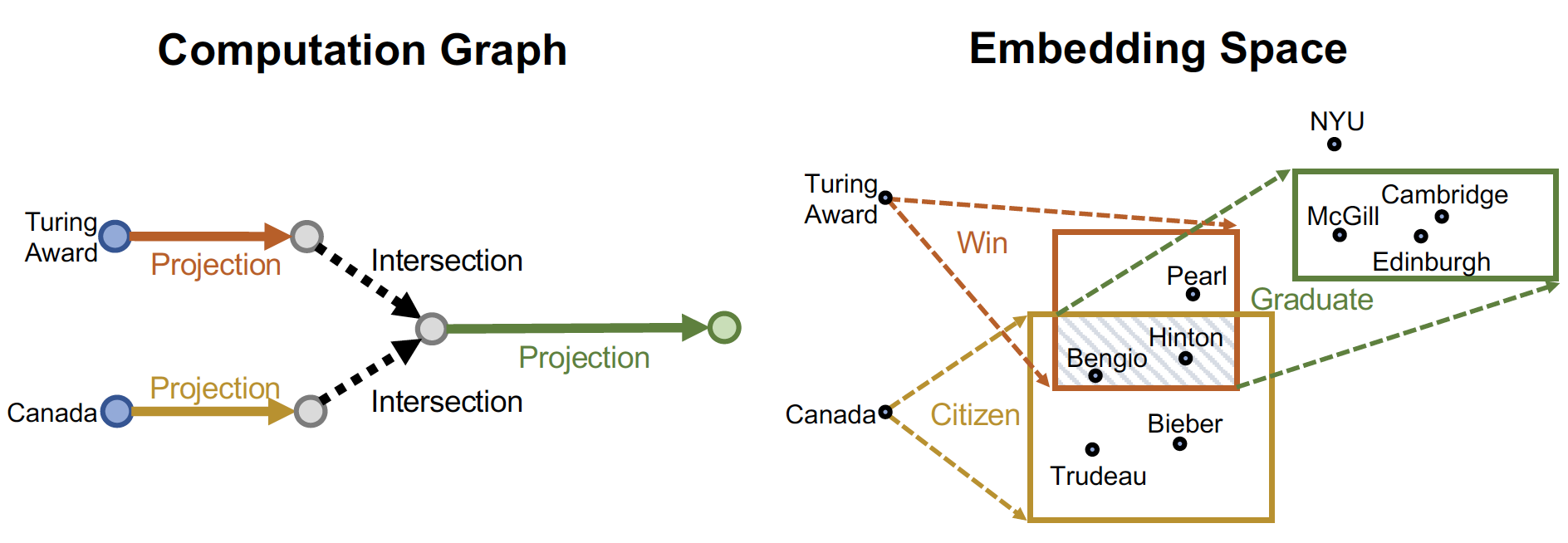
2. Path Query : 조금 더 생각해야 하는 질문 (Winner → Graduate)
3. Conjunctive Query : 교집합 질문 (Canadian & Graduate)
4. EPFO Query : 합집합 질문 (Turning Award | Graduate)

One-hop Query

☛ Where did Hinton graduate?

간단한 one-hop query 는 link prediction 으로 생각할 수 있다

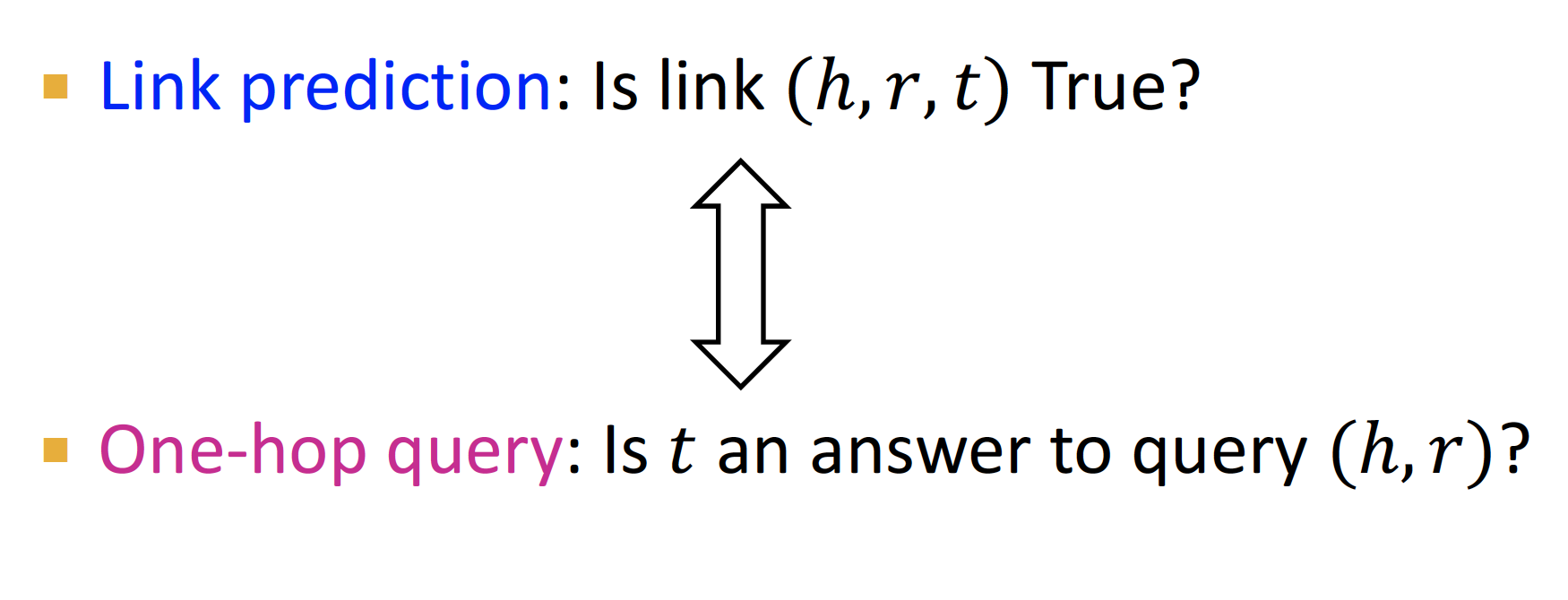
Path Query

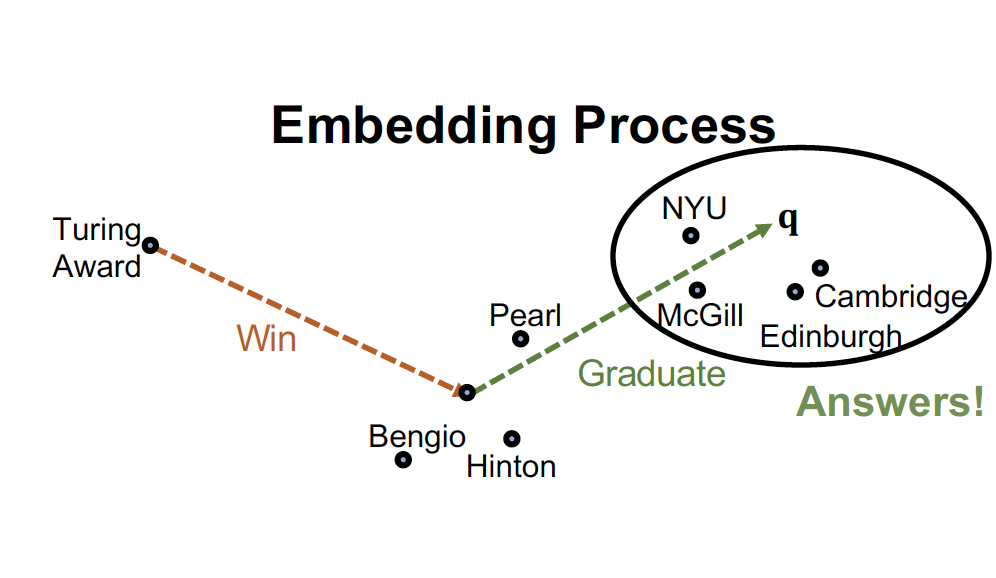
☛ Where did Turning Award winners graduate?

path query 의 경우 one-hop 을 여러 단계로 진행하여 타고 타고 들어가 $V$ 를 찾는다
+= relationship 을 진행하며 최종 answer 를 찾는다

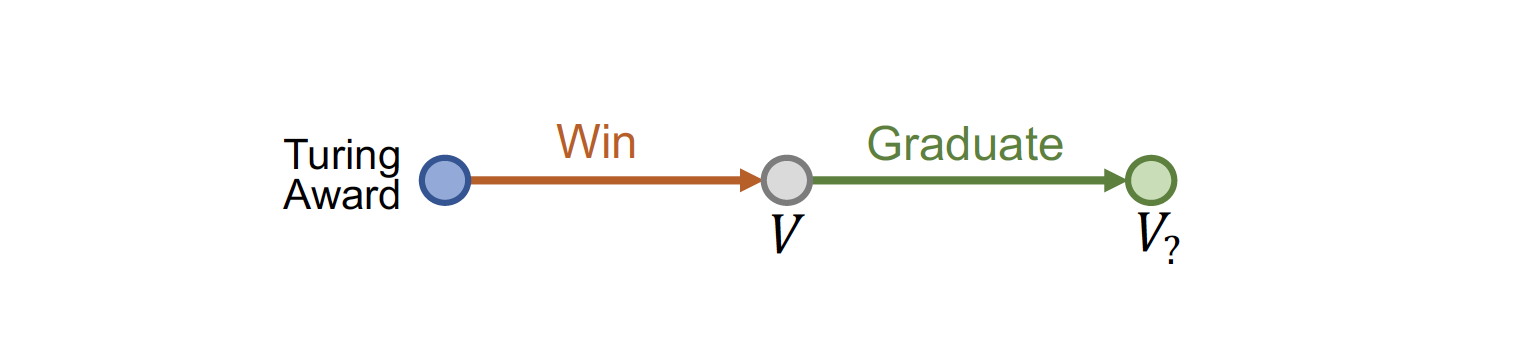
Traversing KG

그렇다면 KG 에서 multi-hop reasoning 을 진행한다면 어떻게 될까 ..

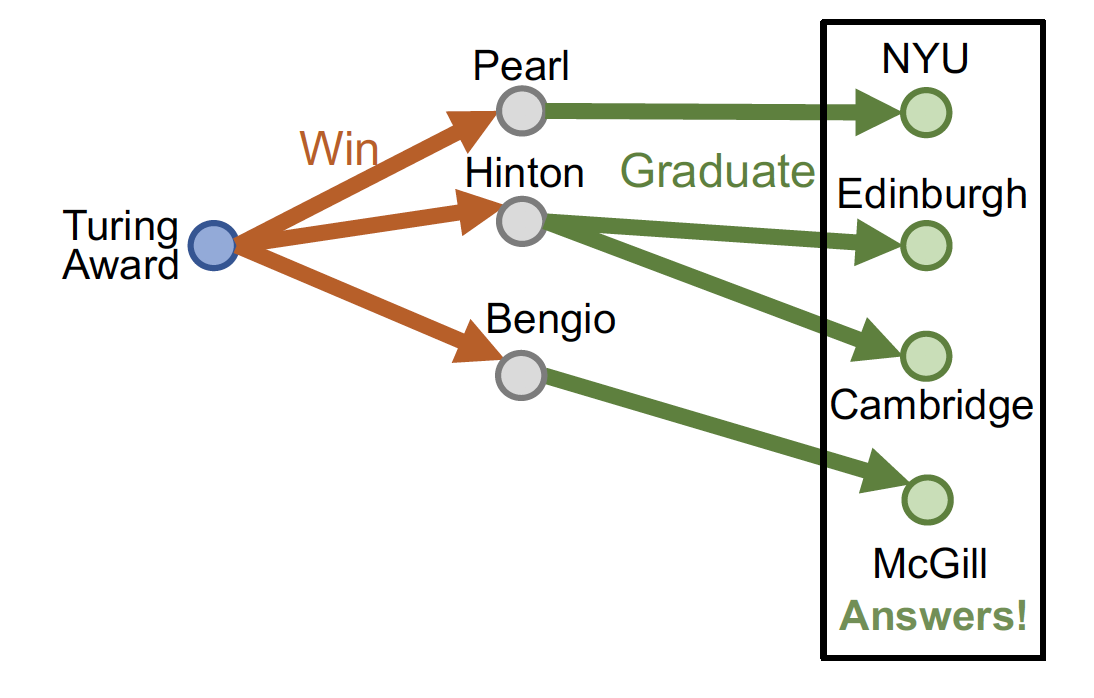
one-hop 을 여러 번 진행하며 그 때 마다 link prediction 을 하게 되면,
→ 모든 step 마다 모든 node 에 대한 확률값을 구하게 된다
→ 시간복잡도는 $O({|V|}^n)$ 으로 어마어마하게 커진다
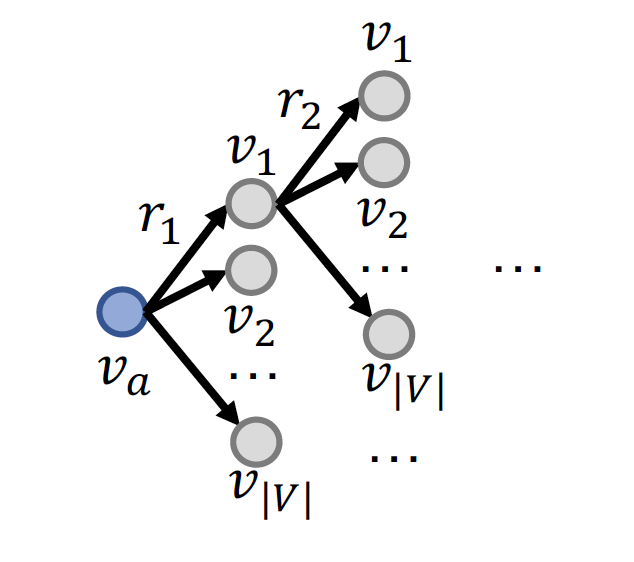
따라서 Query 를 매 step 마다 embedding 한다!
→ 이를 위해 transE 를 multi-hop reasoning 에 사용한다
→ Score Function $f_q(v) = ||q-v||$ 가 되고, 이 때의 시간복잡도는 $O(V)$ !!

4. Conjunctive Queries

☛ Where did Canadians with Turning Award graduate?

복잡한 교집합 질의 (multiple anchor nodes 에서 출발하는 질의) 는 어떻게 다룰까 ~

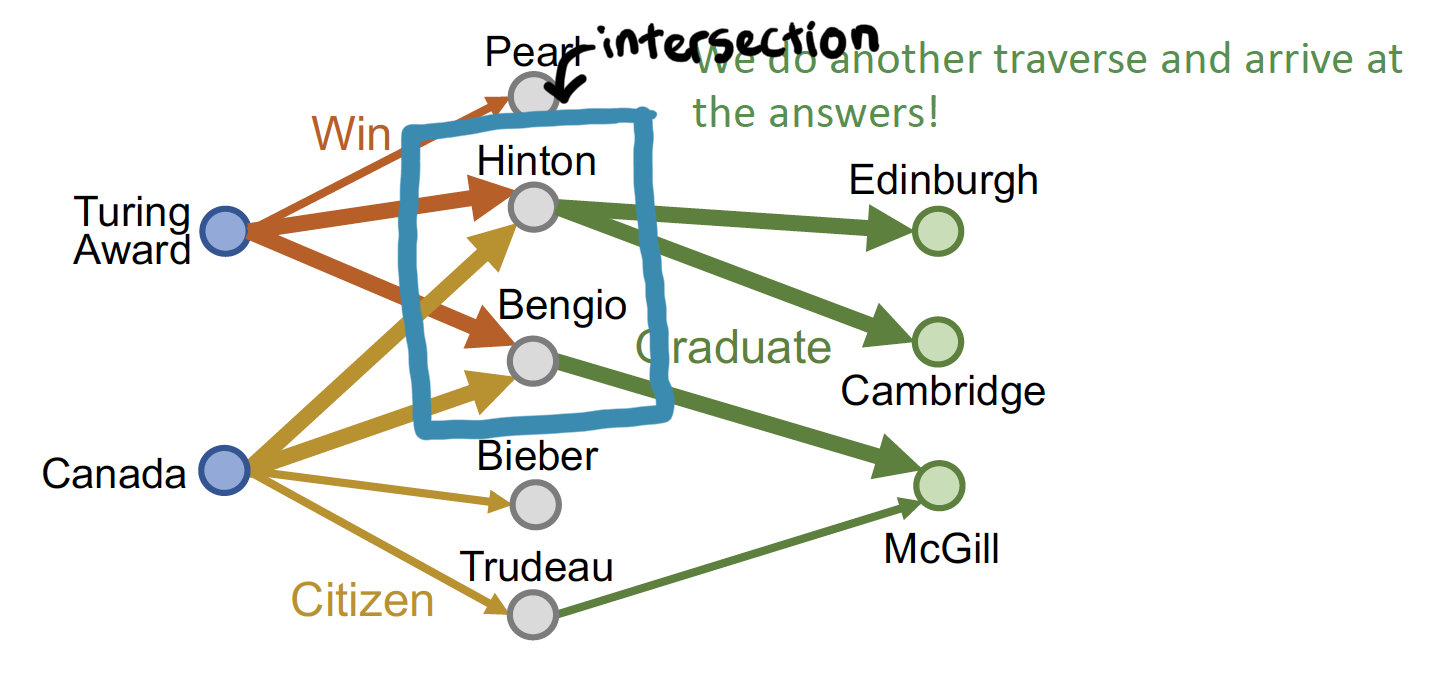
anchor node 에서 각각 출발하여, relation 이 겹치는 node 를 찾는다
여기에서 multi-hop 을 진행한다!

Traversing KG

Path Query 예시에서 Traversing KG 를 할 때, 매 step 마다 embedding 해서 정답을 찾는다고 했는데 ...

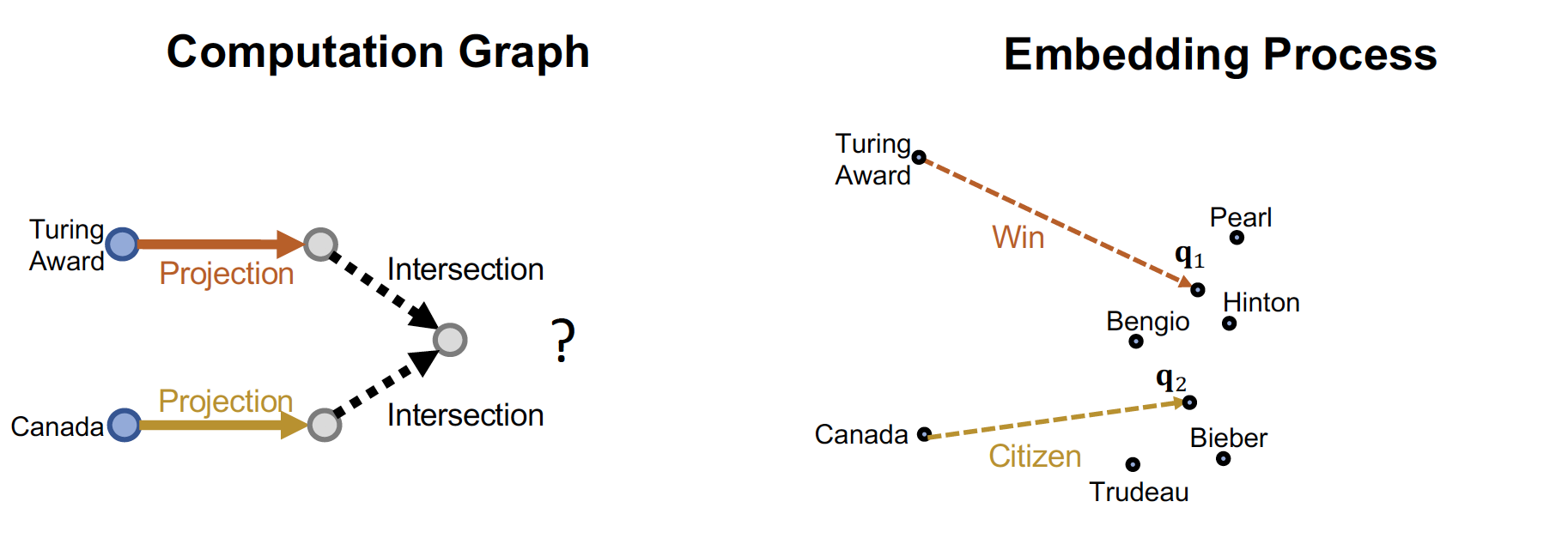
교집합 질문에서 이러한 방법론을 적용하게 되면,
실제 embedding space 에서 하나의 점으로 표현되지 않기 때문에
→ 정확한 intersection 을 찾을 수 없다

따라서 위의 문제를 해결하기 위해, Neural Network 를 이용한다 ~

Neural Intersection Operator

각각의 query 마다 embedding 을 진행하여 neural network 를 통과시키고, 이를 통합하여 Intersection query 를 만들어 낸다

Input : query embedding $(q_1, ... , q_m)$
Output : Intersection embedding $J(q_1, ... , q_m)$
$J$ 는 permutation invariant! (13기 중 우수과제자 = 우수과제자 중 13기 사람)

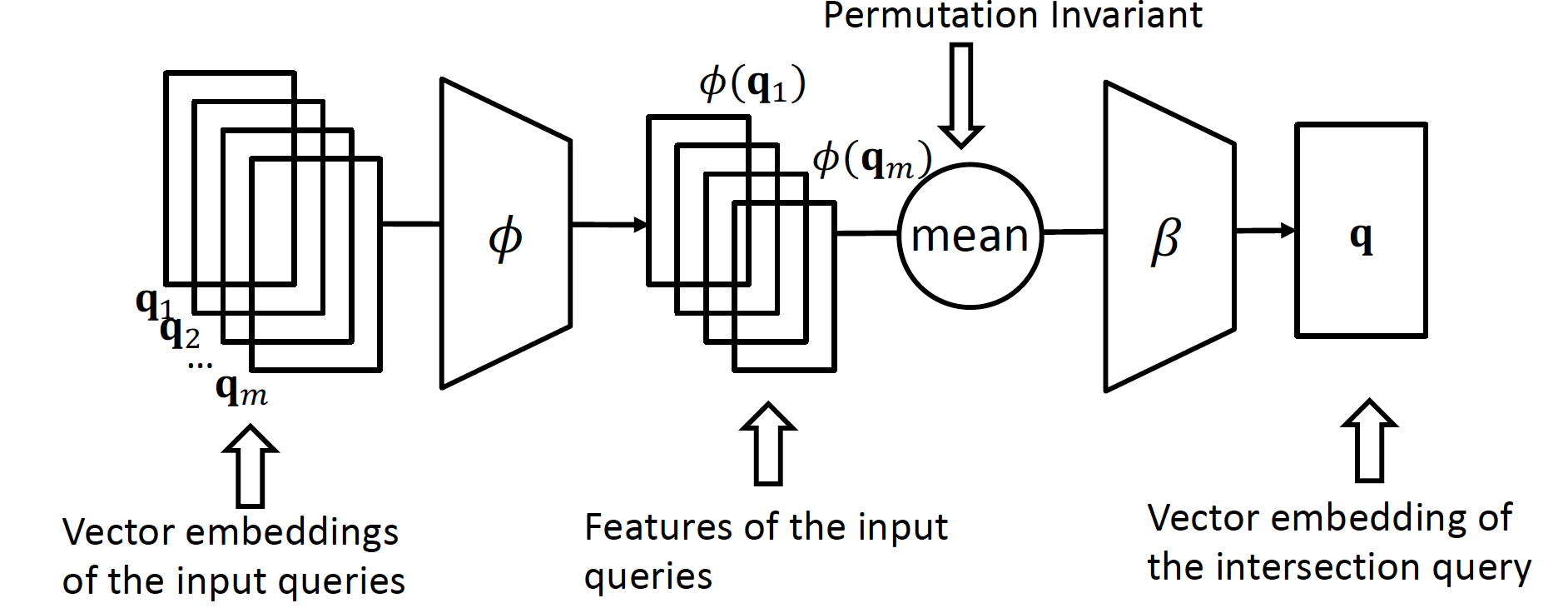
Deepset architecture 를 적용해서 intersection query 의 vector embedding 을 찾는다

$\phi$ 는 $(q_1, ... , q_m)$ 에 각기 다른 가중치를 적용해서, input query 의 feature 를 만드는 역할을 하고
$\beta$ 는 이를 하나로 합쳐서 Intersection embedding 을 만드는 역할을 한다
$\phi$ , $\beta$ 둘 다 Neural Network 구조를 가지며, graph size 에 영향 받지 않는 parameter 로 training 할 수 있다

transE 처럼 학습을 진행하면, intersection embedding space 를 구할 수 있다고 한다 ~

Limitations

그렇지만 Neural Intersection Operator 은,

단순히 intersection vector 하나를 구하는 것이기 때문에 직관적이지 않고
traverse KG 에서 매 step 마다 나올 수 있는 정보를 활용할 수 없으며
기하학적으로 설명하기엔 쫌 아쉽다

따라서 이를 보완한 Box Embedding 방법론이 등장하게 된다 ~

5. Query2Box

query 를 더 이상 vector 로 embedding 하지 않고, Box 로 embedding 을 진행한다 ~

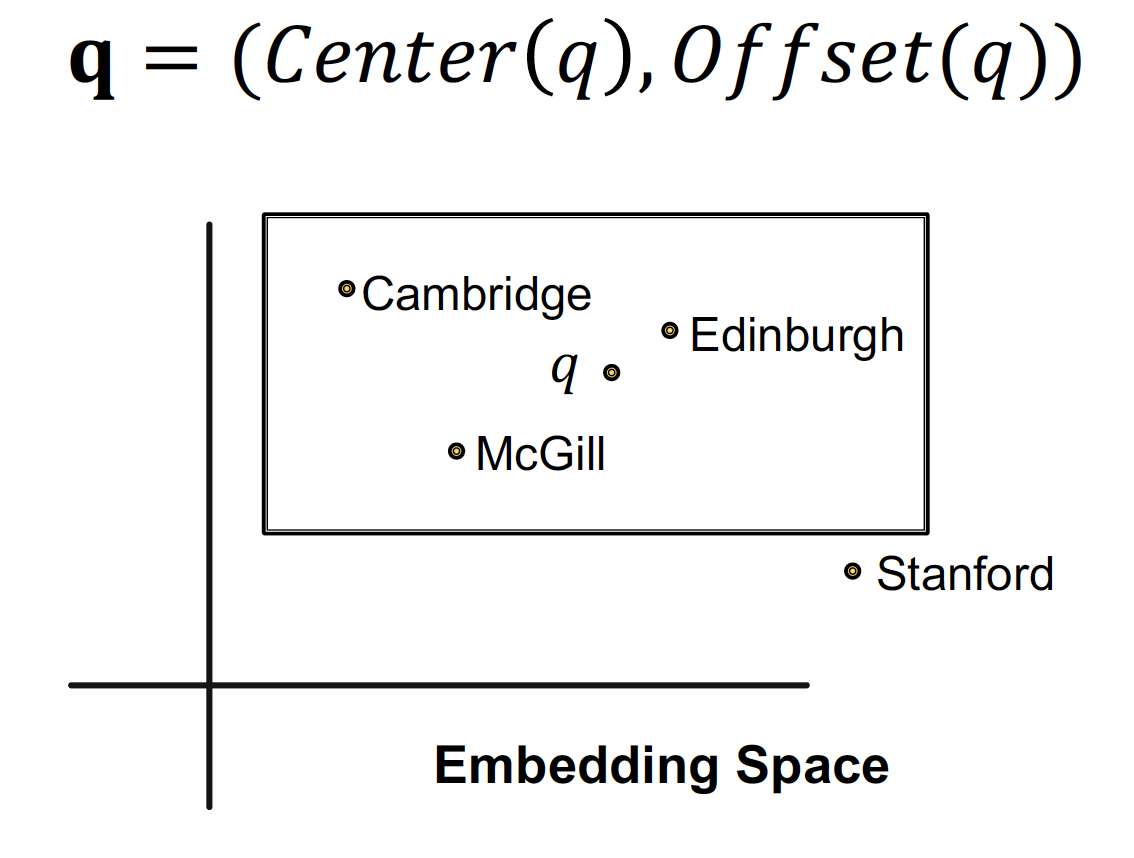
Box Embedding 을 통해서,

vector embedding 은 사람의 판단으로 intersection 을 정해야 하는 단점이 있는데
→ box embedding 은 intersection 영역이 명확하게 정의되므로 훨씬 직관적이다
traverse KG 에서 매 step 마다 나오는 entity 의 경우,
→ box 가 powerful abstraction 역할을 할 수 있다

Projection Operator

input 으로 box 를 받아서 → output 으로 box 를 내보낸다

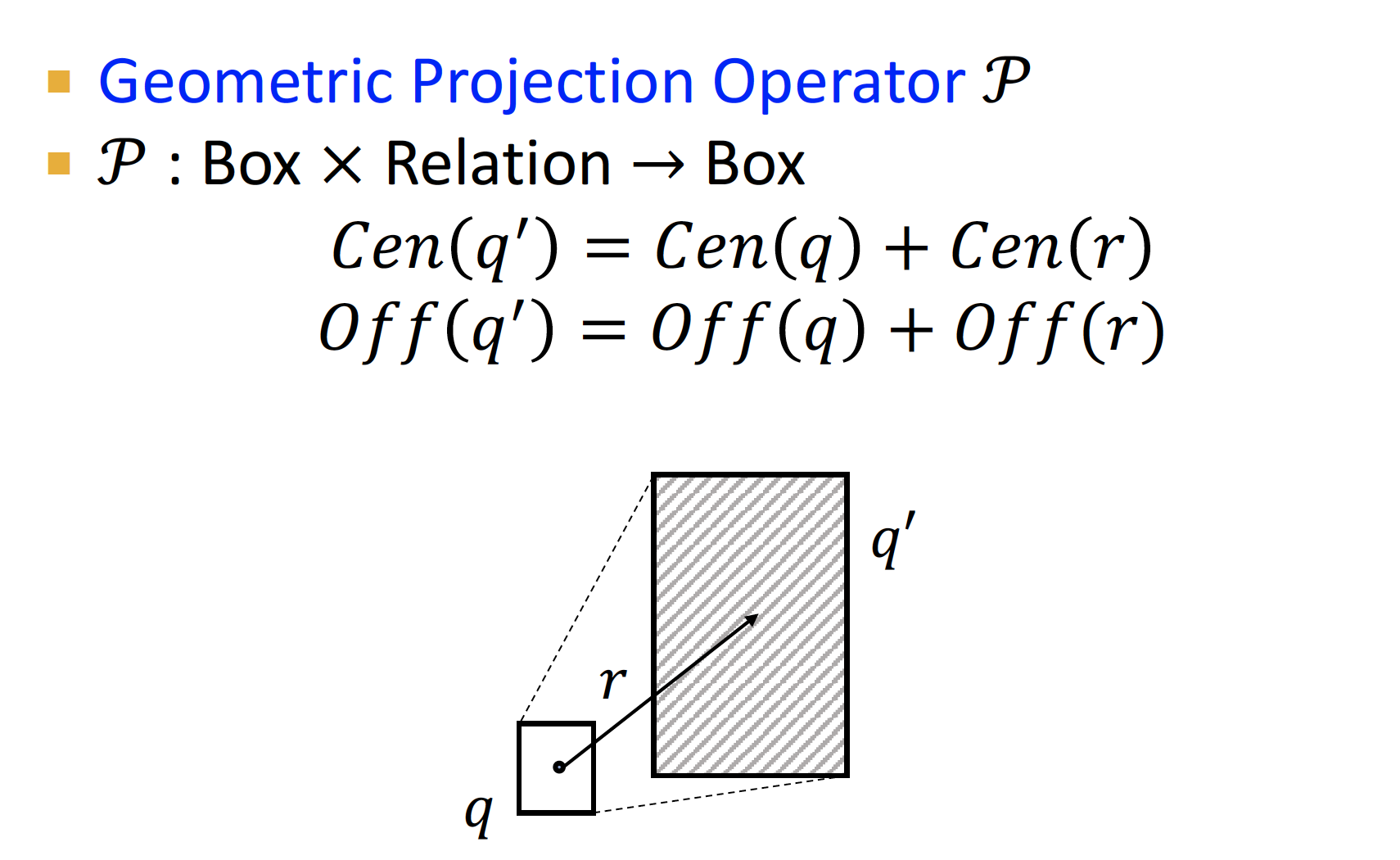
$\mathcal P$ : Box $\times$ Relation 이며,
기존 정보 $q$ 에 + relationship $r$ 을 더해서 = $q'$ 를 만든다!

path 가 진행될 수록 box 는 계속 커지는데,
relationship 정보가 더해질 때 마다 어느 정도의 error 를 감안해야 하기 때문에 박스가 점점 커진다고 한다

Intersection Operator

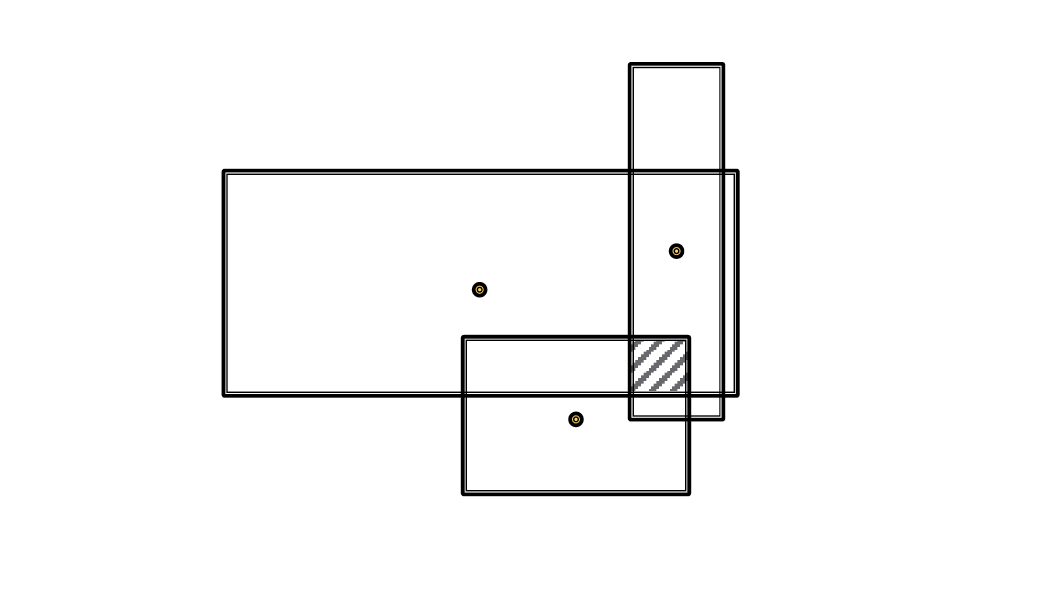
Geometric Intersection Operator $J$ = Box $\times$ ... $\times$ Box = Box
center 는 weighted average 값이 되며, offset 은 상쇄된다

위와 같은 과정을 통해 Box Embedding 이 진행되고, Intersection box 를 찾아서 정답을 찾는다 ~

Entity-to-Box Distance

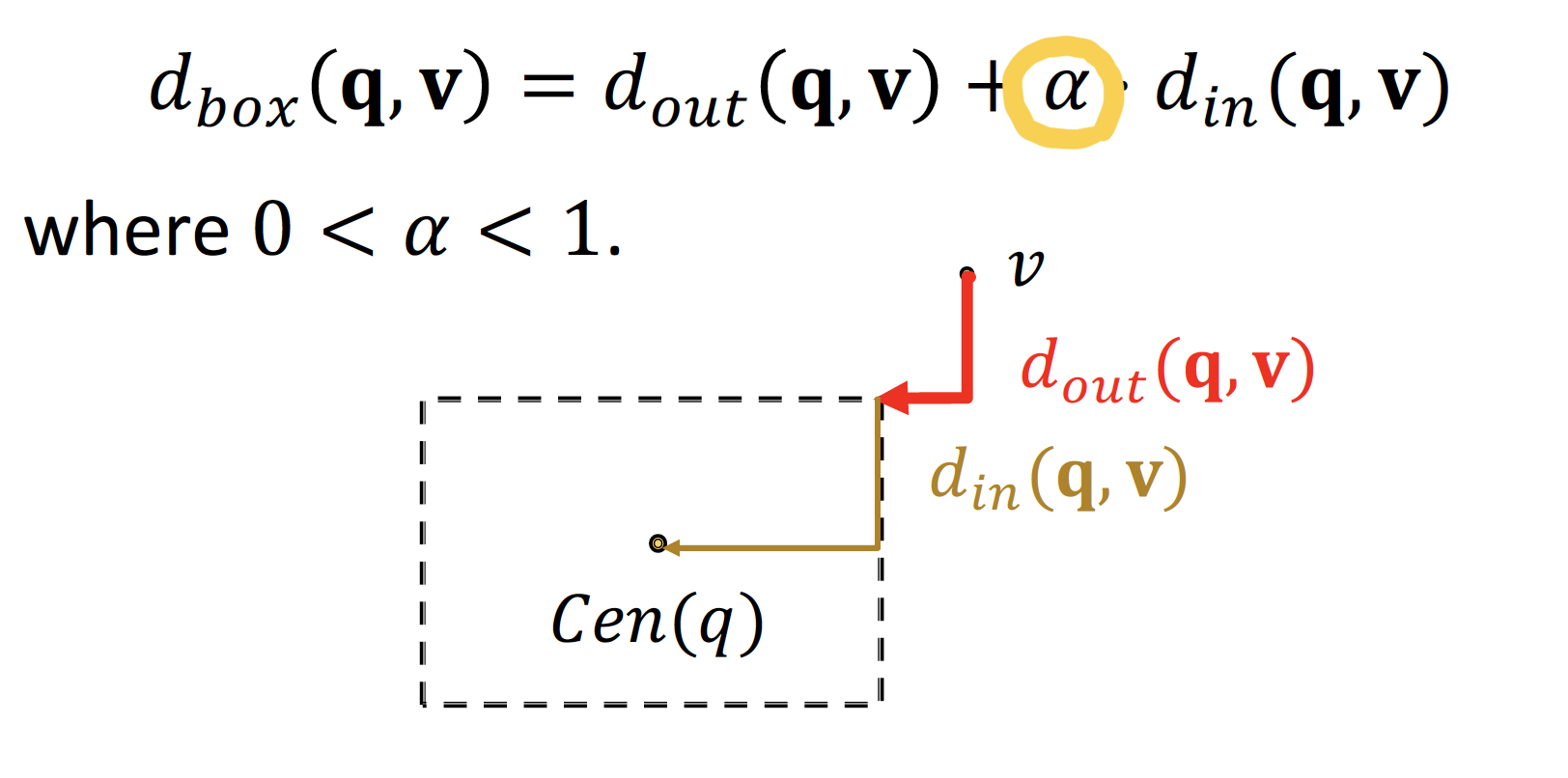
$v$ 를 $q$ 로 나타내고자 할 때, Entity-to-Box Distance 를 고려한다
query box $q$ 와 entity vector $v$ 의 distance 는 L1 norm 으로 정의하며,
parameter $\alpha$ 를 통해 $q$ 의 offset (= 영향력, 중요도) 를 조절할 수 있다

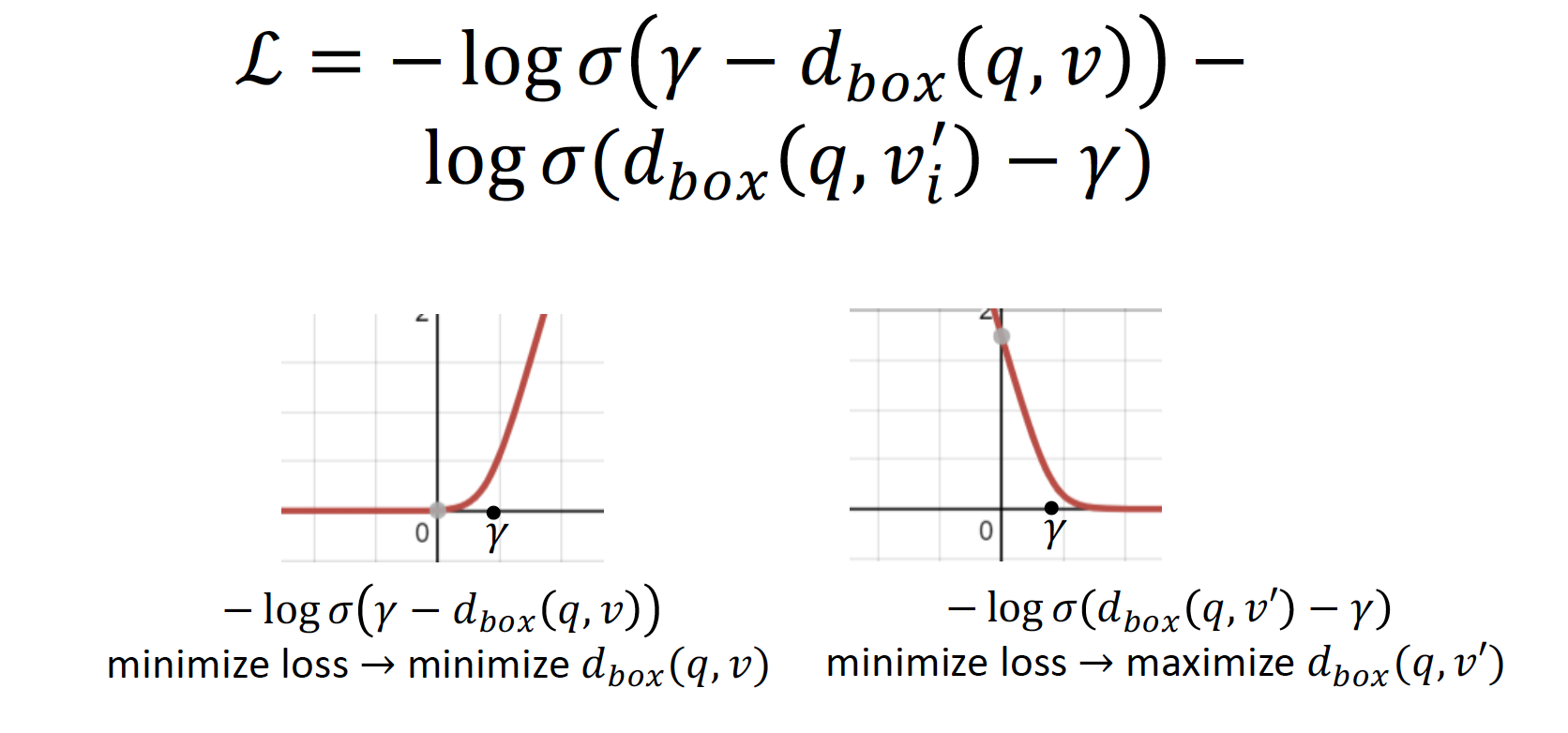
Query2Box 또한, loss $\mathcal L$ 을 minimize 하는 방향으로 학습한다

Positive Box Score 를 minimize 하고,
= {margin $\gamma$ - positive sample $d_{box}(q,v)$ } 값이 클수록
= positive sample $d_{box}(q,v)$ 값이 작아질수록
= positive sample 의 distance 가 작아질수록!
Negative Box 를 maximize 한다

Relation Patterns

Query2Box 는 Symmetry, Composition, 1 to N / N to 1 / N to N 관계 모두 표현이 가능하다고 한다 ~

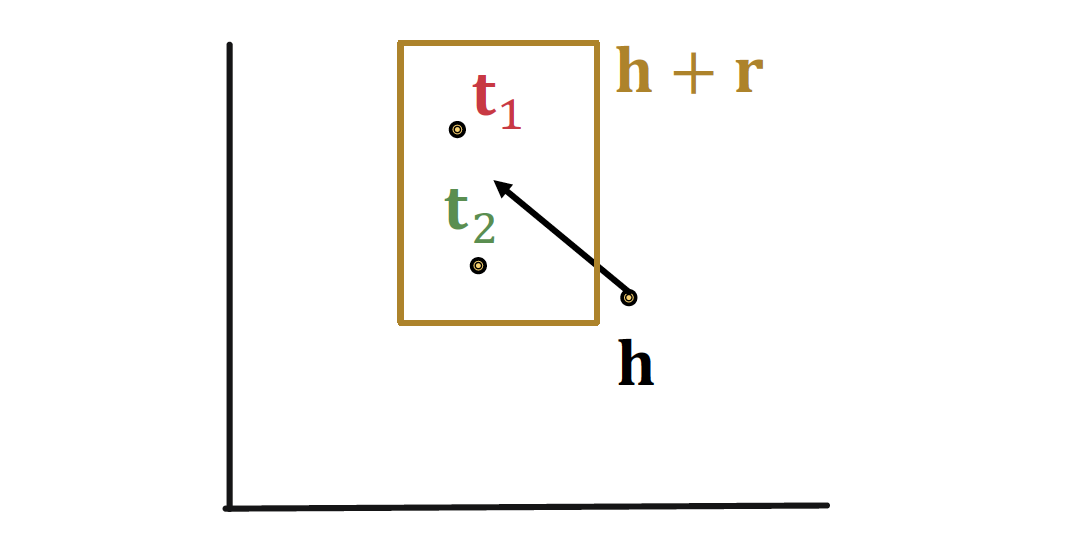
N-array Relations
(𝒉, 𝙧 ) 에 대해 $t_1$ , $t_2$ 가 모두 Box 안에 포함된다
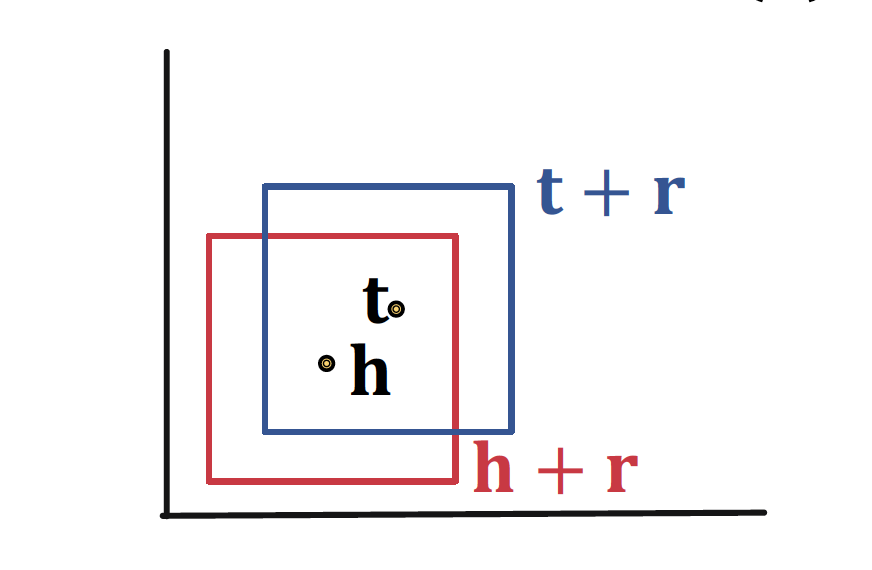
Symmetric Relations
Cen(r) = 0 으로 설정하면, 𝒉 + 𝙧 = 𝒕 , 𝒕 + 𝙧 = 𝒉 모두 Box 내에 존재한다
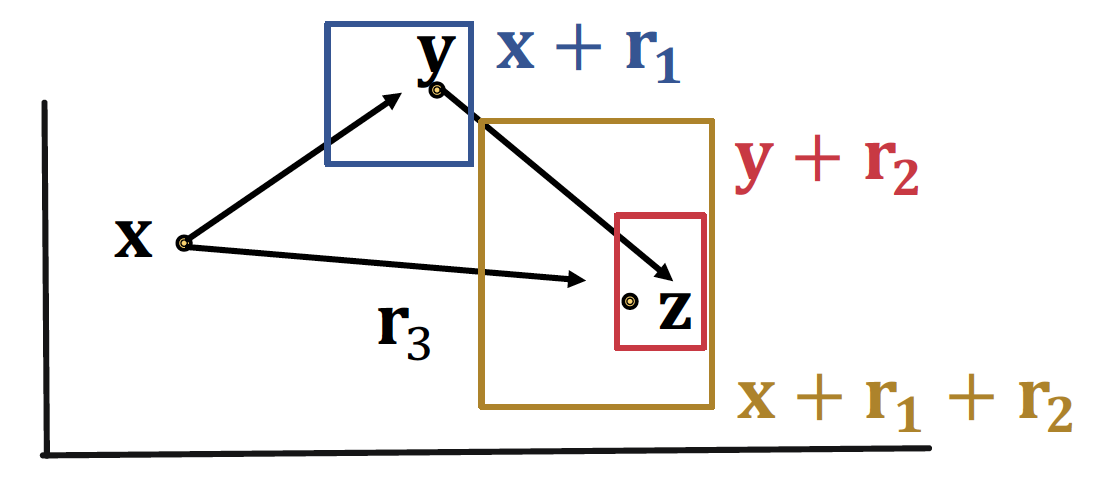
Composition Relations
$r_3 = r_1 + r_2$ 이며, $y = (x, r_1)$ 이고 $z=(y, r_2)$ 일 때,
$z=(x, r_1+r_2)$ 가 되므로 Box 를 통해 표현 가능하다