Contents

1. Network Properties
2. Random Graph Model
3. The Small-World Model
4. Kronecker Graph Model

1. Network Properties

Key Network Properties

4가지 요소로 네트워크를 평가한다 ~
1. Degree Distribution : P(k)
2. Path Length : h
3. Clustering Coefficient : C
4. Connected Components : s

1. Degree Distribution

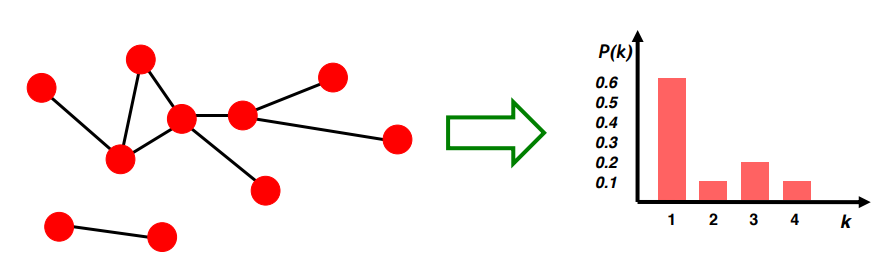
내가 랜덤으로 뽑은 노드가 degree = k 를 가지고 있을 확률
위의 그림에서는 60%가 degree=1

2. Paths

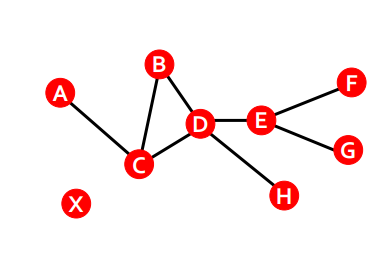
노드들이 지나 온 경로! ex. ACBDEFG

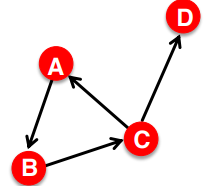
여기서 추가적으로 파생된 개념 1. distance

• 노드들 사이의 엣지가 몇 개나 있는지로 체크
• directed graph 의 경우, $h_{B,C}$ ≠ $h_{C,B}$
• $h_{B,C}$ = 1, $h_{C,B}$ = 2, $h_{A,D}$ = $\infty$ (연결 X)

개념 2. Network Diameter
두 개의 노드 사이에 가장 먼 거리
diameter 개념만은 잘 안 쓰고, average path length 씀

3. Clustering Coefficient

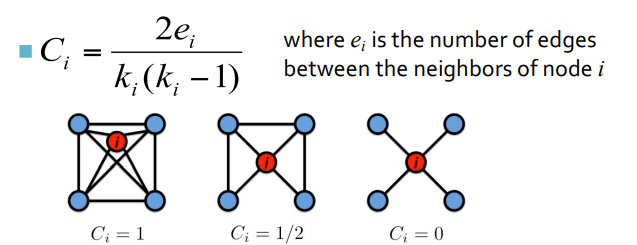
노드 i에 대해, 해당 노드와 다른 노드들이 얼마나 잘 연결되어 있는지를 나타내 주는 값 (how much do they know each other~?)

• 2번째 그림 : (2x3)/(4x3) = 1/2
  모서리의 네 개의 점에 대해서, 3개의 edge 존재 : $e_i$ = 3
• 3번째 그림 : (2x0)/(4x3) = 0
  모서리의 네 개의 점이 서로서로 알지 못함 : $e_i$ = 0

이를 통해 구한 값을 다 평균 취해서, average clustering coef 구함!

4. Connectivity

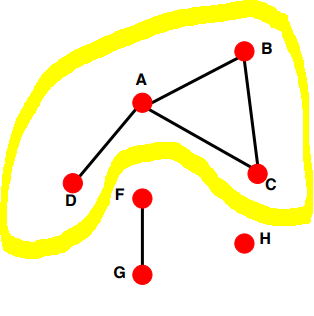
가장 큰 component의 크기 (Size of the largest connected component)

Real World Network

MSN Messenger

MSN 메신저를 사용하는 유저들의 네트워크는 어떻게 구성되어 있을까 ~?

1. Degree Distribution (log-scaled)

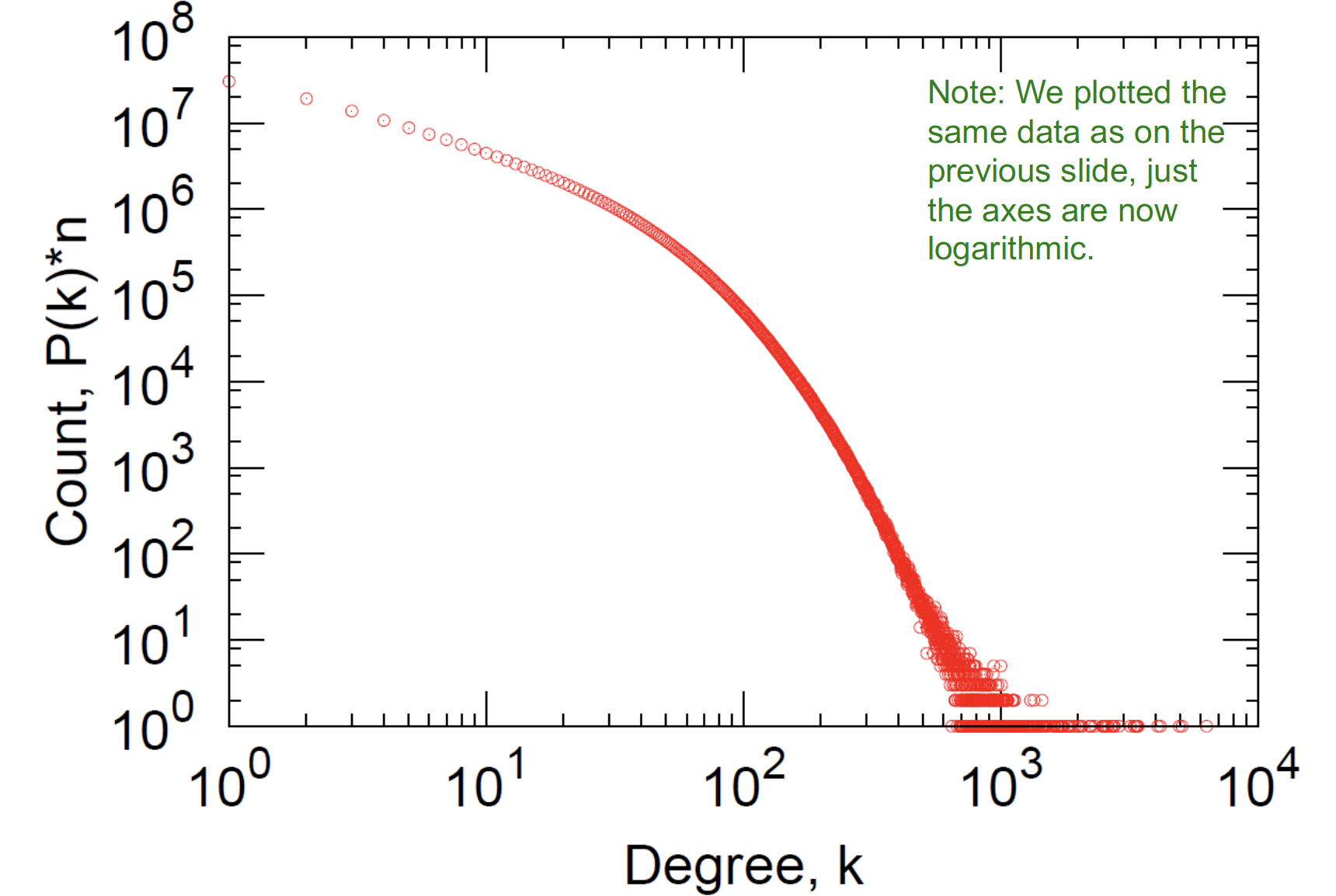
log를 취하지 않으면, 굉장히 right-skewed 된 형태를 보임
대부분의 degree 매우 낮고 (0값에 몰려 있음) + degree 큰 노드 많지 않다

2. Clustering

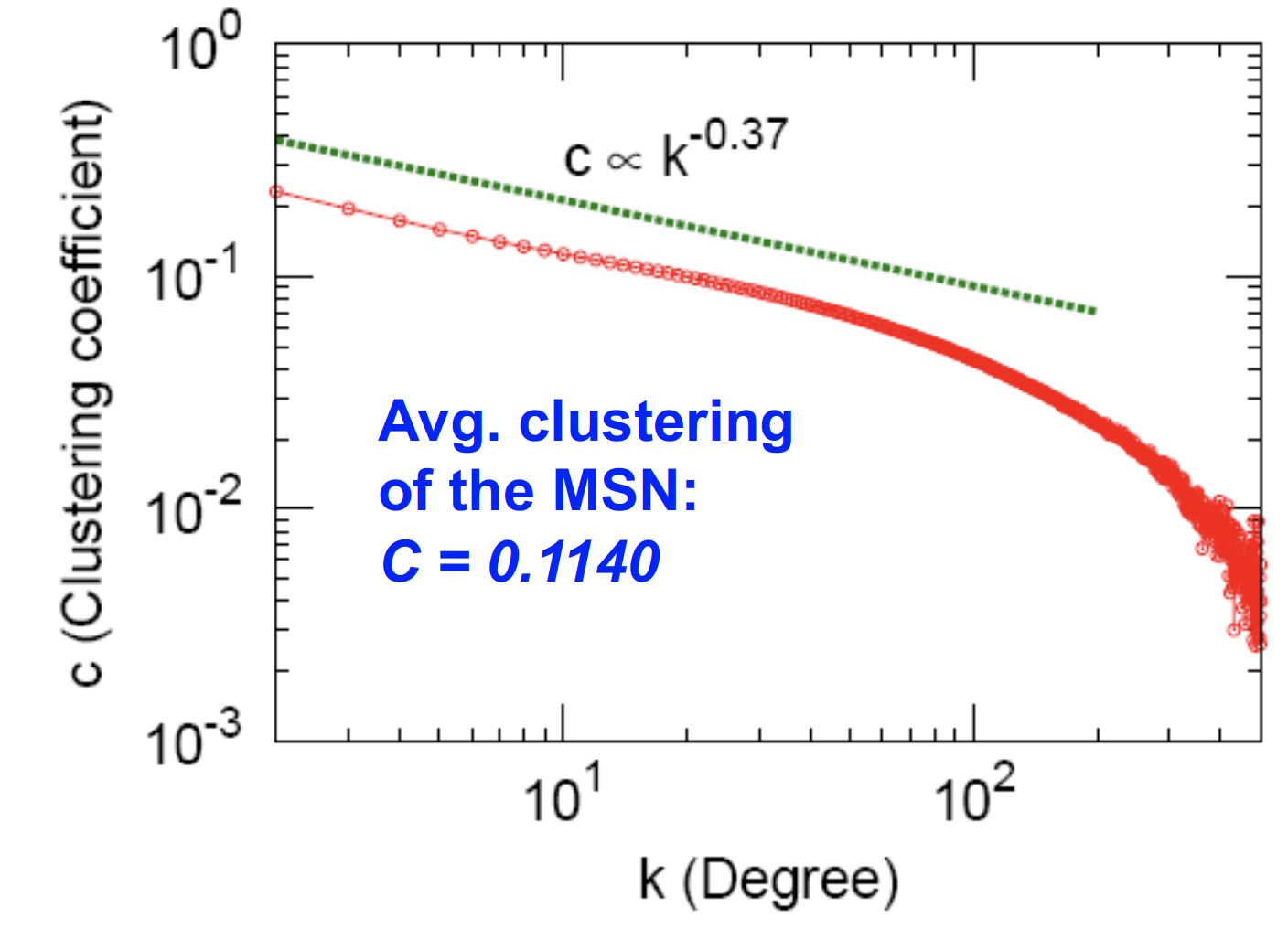
Avg. Clustering C = 0.1140 : 11% 정도의 친구들이 서로서로 잘 알고 있다

추가로 알게 된 내용!
C와 K는 반비례 관계이다 = degree가 높은 node일 수록, 이웃들 간의 연결 계수(C)는 작아진다
예지니가 너무 좋은 예시를 들어 줬는데, 인스타를 예로 들면,
지드래곤 같은 경우 전 세계 가지각색의 사람들이 following을 하고 있을 것이므로 following 하는 사람들 사이에 연결점이 많이 없겠지만,
나의 경우 내가 활동하는 집단들에서의 친구들이 나를 following 하므로 친구들 사이에 연결점이 많이 존재할 것!
따라서 C가 커질수록 K는 작아진다 ~

3. Connected Components

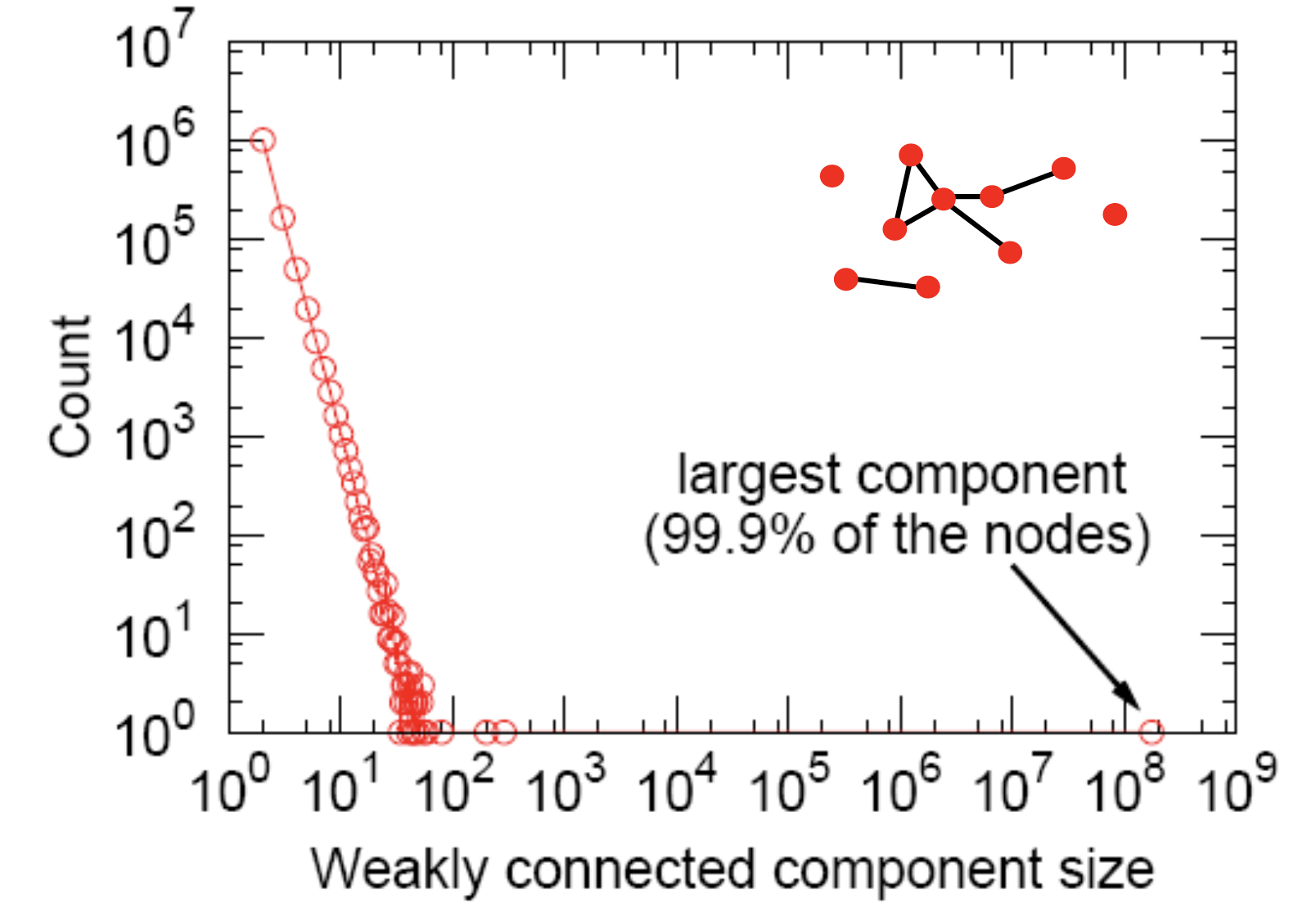
giant component! ($10^8$) = 99.9% 노드를 가진 큰 component

4. Diameter of WCC

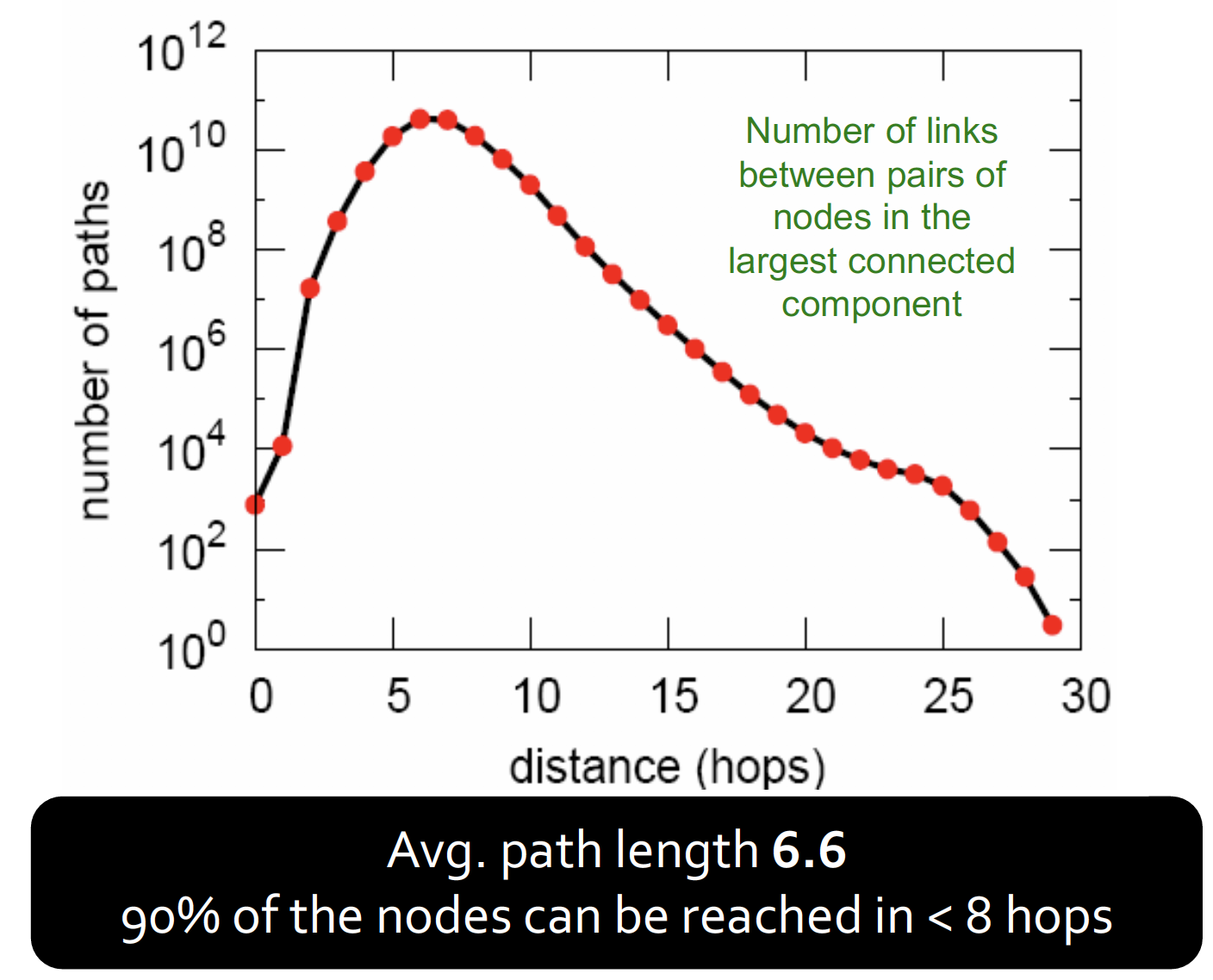
한 사람으로부터 다른 사람으로 갈 때 얼마나 많은 단계를 거쳐야 하는지
(BFS 촌수계산 문제가 생각이 났음..ㅎㅎ)

들으면서 생각난... 6단계 법칙

지구에 있는 모든 사람들은 최대 6단계 이내에서 서로 아는 사람으로 연결될 수 있다!
한국의 평범한 원생인 내가 친구의 친구의 ... 친구를 거치면 미국 대통령까지 만날 수 있다는 사회 이론이다
MSN Messenger 에서도 Path length=6.6 이어서, 우와 신기하네 했다

2. Random Graph Model

가장 easiest 하고 simple 한 graph model
정의 그대로 Random Graph (stochastic random event)
심플하고 랜덤하게 (unique하지 않게 그때그때마다) 그래프를 생성한다

$G_{np}$ : undirected graph에서 n개의 node들이 있을 때, 각 edge(u,v)의 확률 p가 iid 임을 가정

1. Degree Distribution

binary distribution을 따른다
P(k) 에 대한 식을 정리해 보면, 전체 node 개수는 n개이고, k개의 node와 연결되어있는 node는 나머지 (n-1)-k개와 연결되어 있지 않다
따라서 n-1 개 중 k개를 고르는, binary distribution을 따른다

이항 분포의 정의에 따라, degree k의 평균과 분산은 왼쪽처럼 나타낼 수 있으며,
대수의 법칙에 따라 n의 size가 커지면 0으로 수렴한다

추가적으로,
n이 매우 커질 경우 P(k)는 Poisson dist를 따른다고 한다.

2. Clustering Coefficient

3. Path Length

Expansion alpha

• Expansion : subset 에서 edge가 퍼져 나가는 정도
• 그래프에서 S가 V의 부분일 때, S->V로 가는 edge 수의 최솟값을 expansion alpha 라고 한다

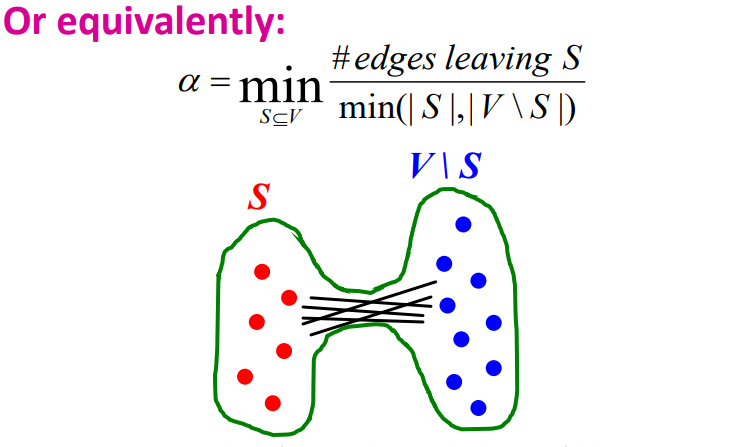
alpha는 위와 같이 표현 가능!

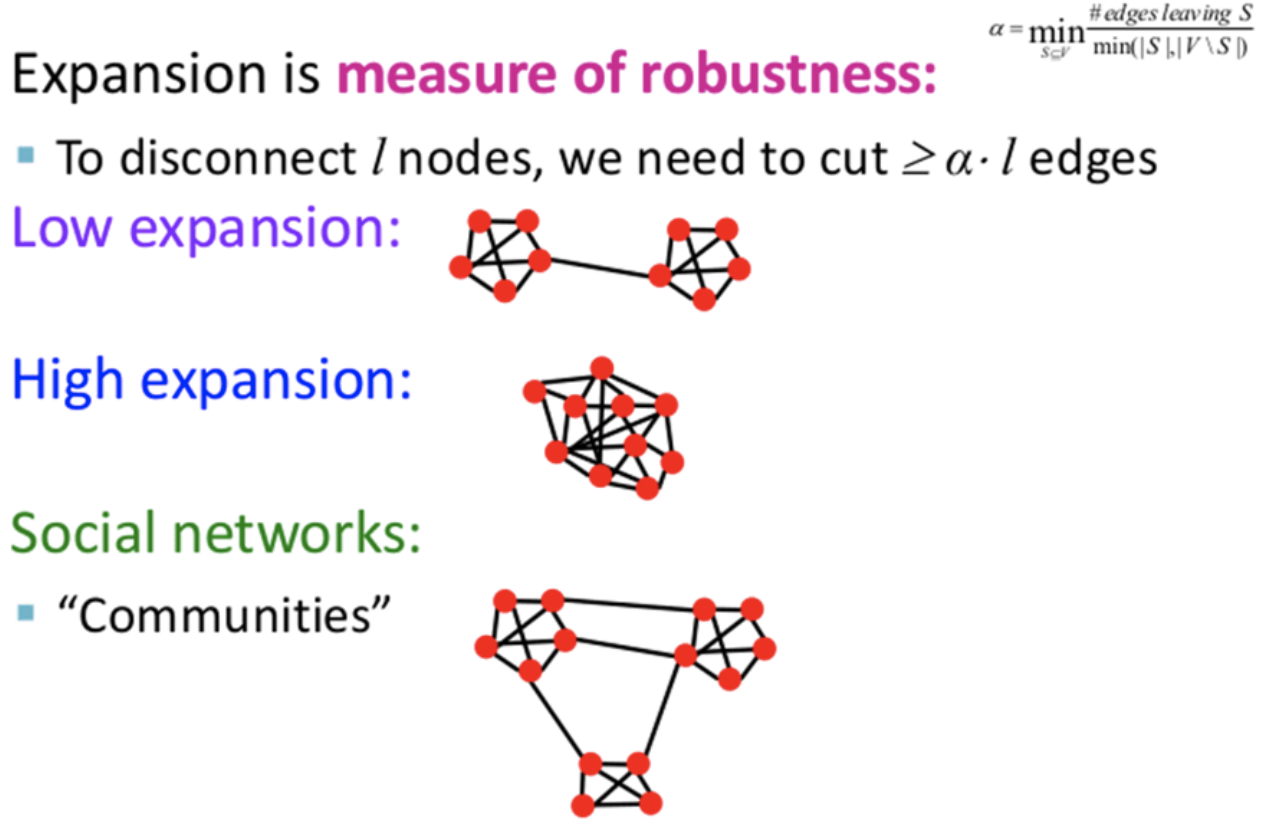
expansion은 robustness를 표현해 준다
expansion이 작다는 것은, 응집이 적게 되어 있다는 것을 의미하고,
expansion이 크다는 것은, 응집이 매우 많이 되어 있어서, S 집합과 V 집합을 분류하려면 많이 끊어 내야 한다는 것을 의미한다

$S' = \alpha * S$
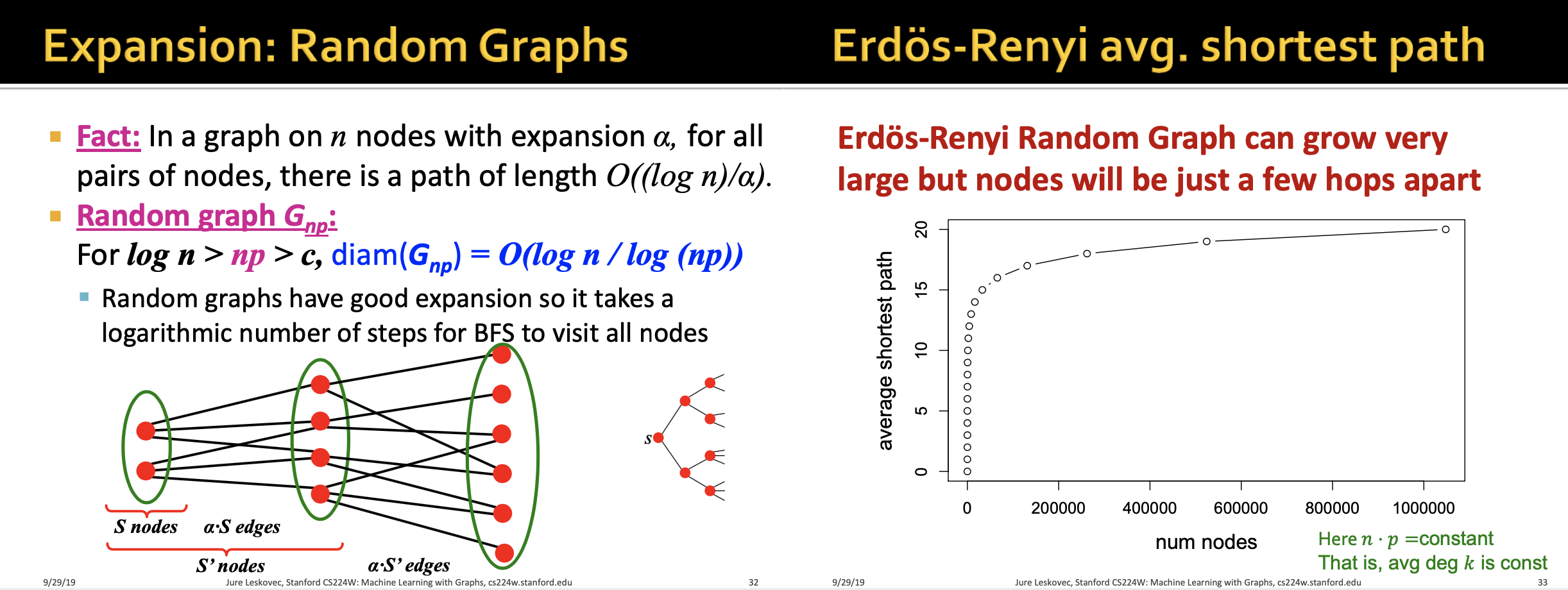
모든 노드를 구할 때 까지 반복하여 path를 구한다
그래프 크기에 비해 짧은 경로를 가지게 된다

MSN vs $G_{np}$

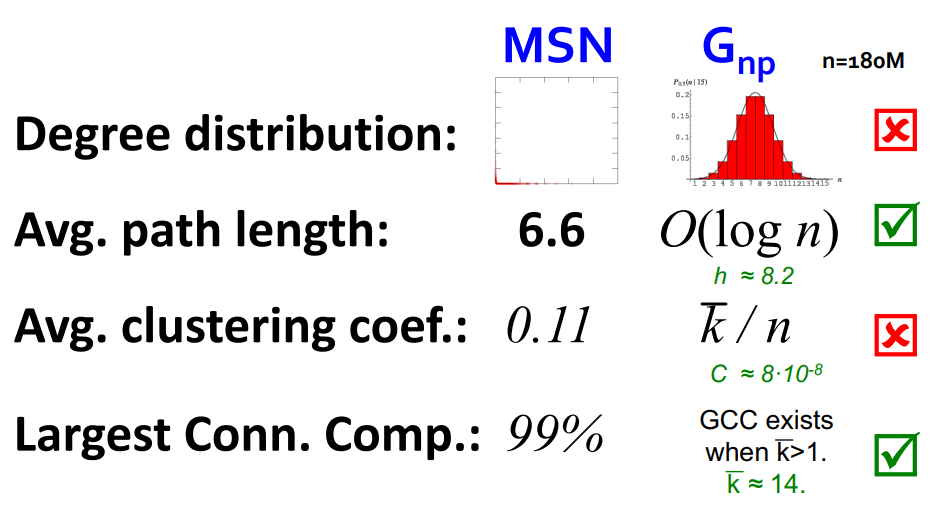
random graph가 실제 네트워크를 잘 반영해 준다면 너무 너무 좋겠지만...
clustering coef 값이 실제 데이터에 비해 굉~장히 낮다
그리고 real world가 random 하지 않기 때문에.. random graph 모델이 실제 상황을 반영하기가 어려울 수 밖에 없음.....

따라서 The Small-World Model 이 나오게 된다 ~

3. The Small-World Model

Controversy

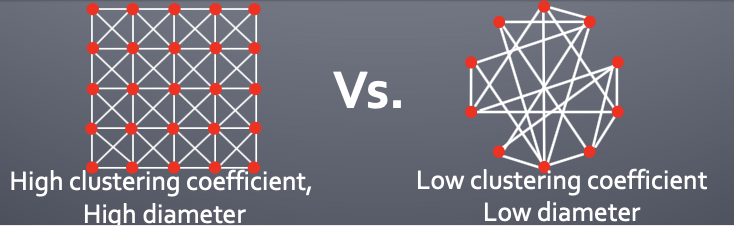
real world = high clustering & small diameter
이걸 동시에 어떻게 표현할까 ~?

Rewire

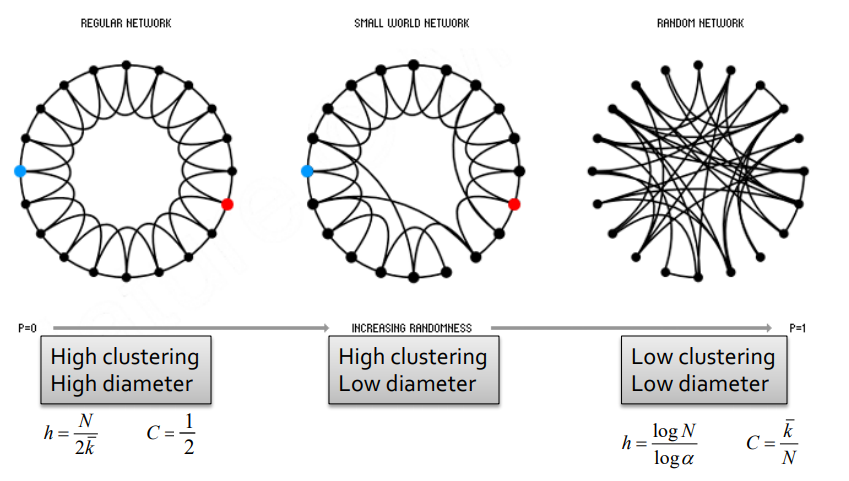
1. Start with a low-dimensional regular lattice
2. Rewire : introduce randomness

낮은 dimension의 lattice(격자)에서 시작해서 high clustering coef 만들고,
랜덤으로 서로 연결된 것을 끊어서 다른 점에 연결한다 ~

지니의 행운의 편지 예시.. (ㅋㅋ)
이 편지는 백만년 전에 시작했고... 동일한 내용의 편지를 6명에게 주지 않을 시 당신은 최고 불행에 처할 수 있습니다 라는 행운의 편지를 받았다면
내 지인에게만 주는 것이 아니라 가끔은 안 친한 사람들한테도 줘야 한다는 것을 의미.....

4. Kronecker Graph Model

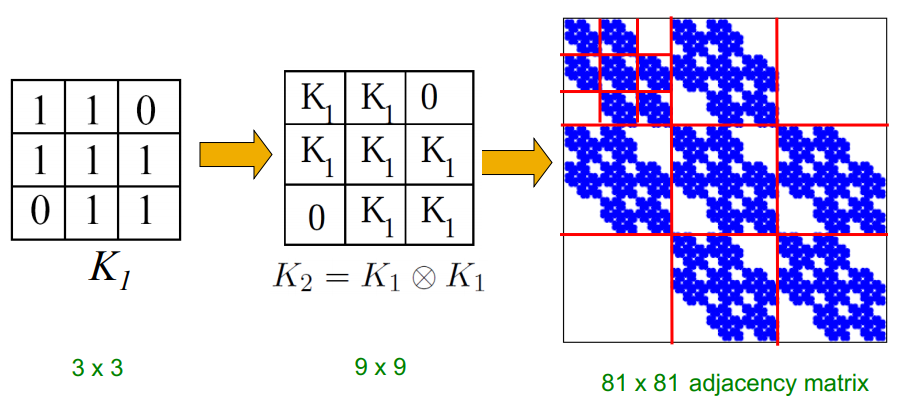
네트워크가 Self-similarity의 특성을 갖고 있음에 착안하여, Recursive하게 네트워크 구조를 형성한다
3x3 K1이 그대로 K2의 한 행으로 들어가서 K2는 9x9가 되고, 이게 계속 반복되는 것...

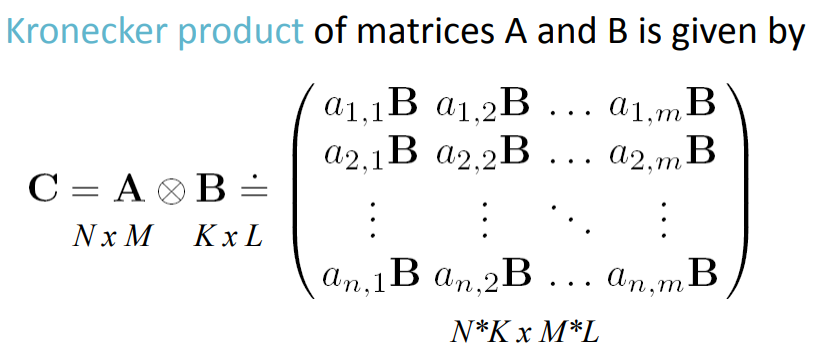
Kronecker Product : 인접행렬간의 행렬곱 (위의 그림)

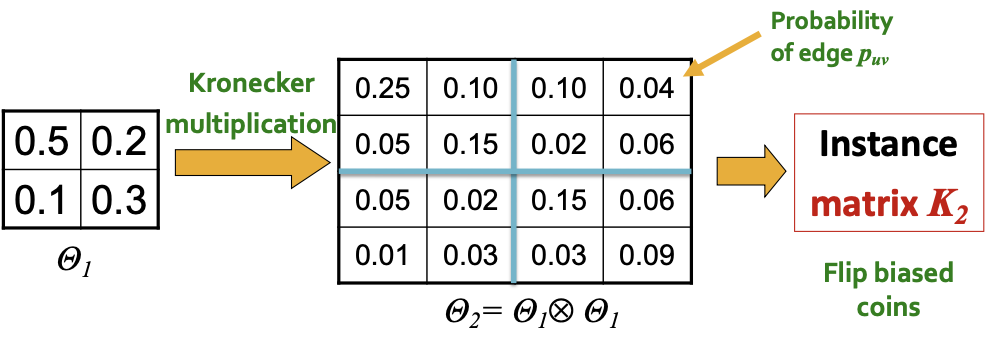
이런식으로 계산 ~
(1,1) : 0.5 x 0.5 = 0.25
(1,2) : 0.2 x 0.5 = 0.10
(1,3) : 0.5 x 0.2 = 0.10
(1,4) : 0.2 x 0.2 = 0.04
...

Drop Edge

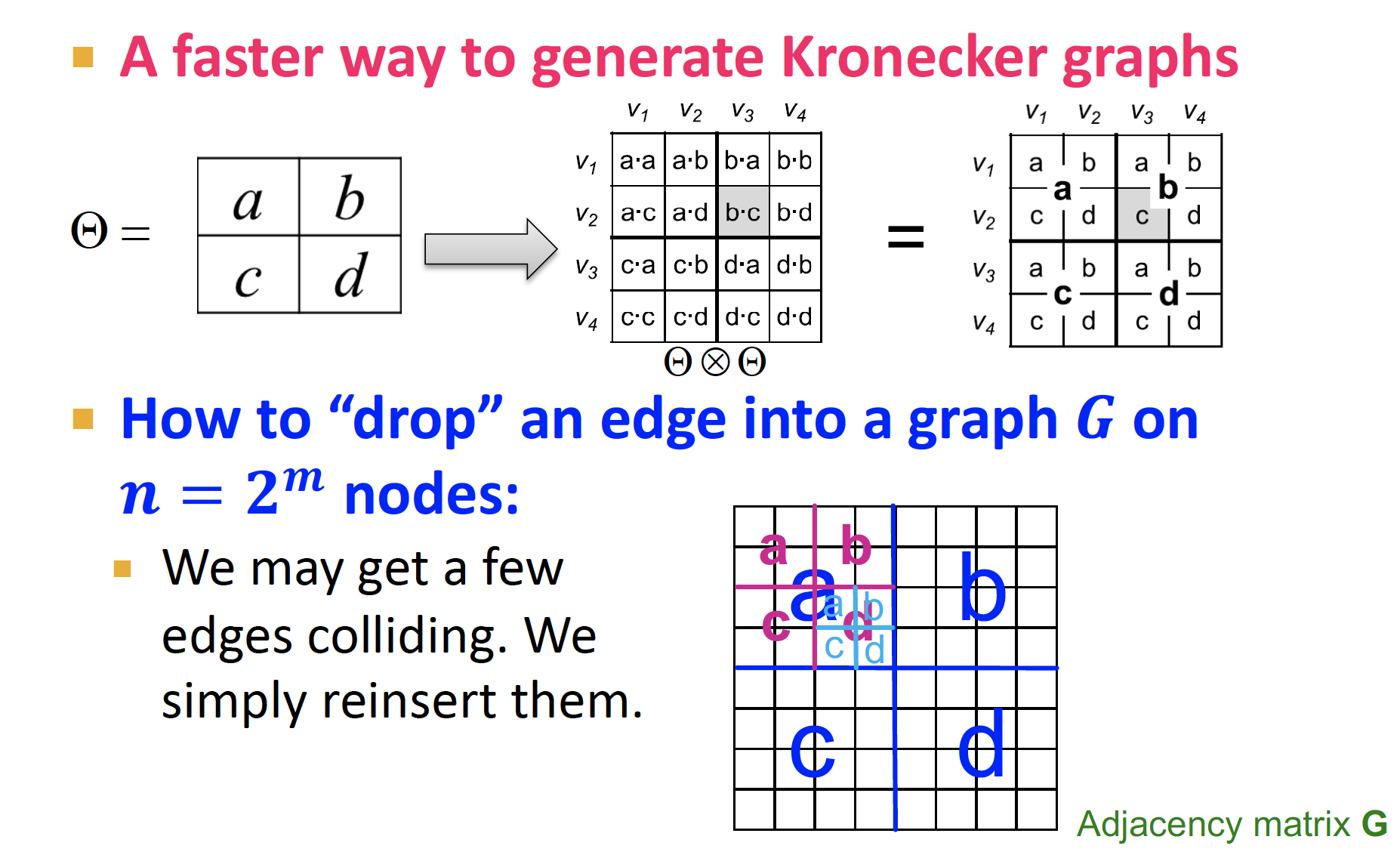
랜덤으로 edge 정해서, 하나씩 drop 하는 것
위의 계산처럼 셀 값 하나 하나를 곱하게 되면 (cell-by-cell product),
연산량이 점점 늘어나게 된다
따라서 Re-insertion 을 통해 연산량을 줄이자 ~
이 때 metropolis-hastings algorithm을 통해서 update 한다

기회가 되면 나중에 Kronecker Graph 에 대한 논문 도 읽어 보는 걸루.. ㅎㅎ

글구 공부하면서 프랙탈 생각났음...

Reference

1. 머쨍이 예지니의 띵강 & 벨로그 리뷰
2. 12기 똑똑이 진혁이 2강 리뷰

---

1. 나무위키 6단계 법칙
2. Network Science - Random Network (Erdös-Rényi Network)
3. Kronecker Graph Model 최적화 방법
4. CS224W Review Post