Contents

1. Subgraphs
2. Motifs & Graphlets
3. Role & Applications

1. Subgraphs

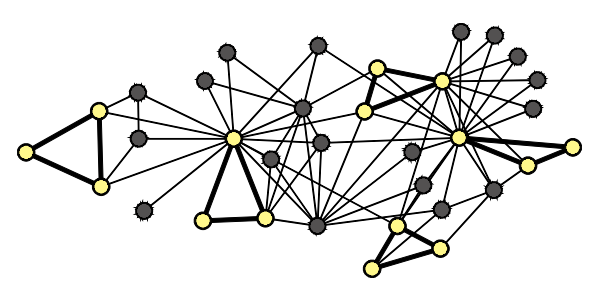
네트워크를 구성하는 부분집합!
small building blocks가 모여서 big network를 구성한다!
subgraph를 통해 network를 characterize 하고 discriminate 할 수 있다 ~

레고 큐브 하나하나가 subgraph가 되고, 레고로 만든 결과물이 network

Case Examples of Subgraphs

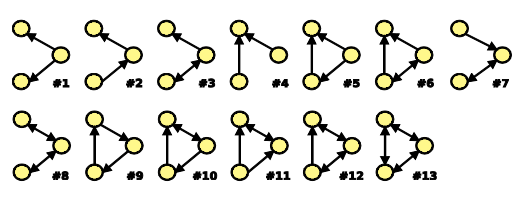
위의 그림은 size=3 인 non-isomorphic subgraph의 예시 ~

• isomorphic (동형) : 돌리면 똑같은 그래프 되는 것
  They are the same graph, they're just drawn in the different way.
  same edges & same directions 가지고 있다
• non-isomorphic (비동형) : 본질적으로 다른 그래프

Significance

그럼 각각의 subgraph들이 얼마나 네트워크에서 중요한지 알 수 있는 방법이 뭘까..?
→ frequency와 occurence 를 이용해 significance를 구한다 ~

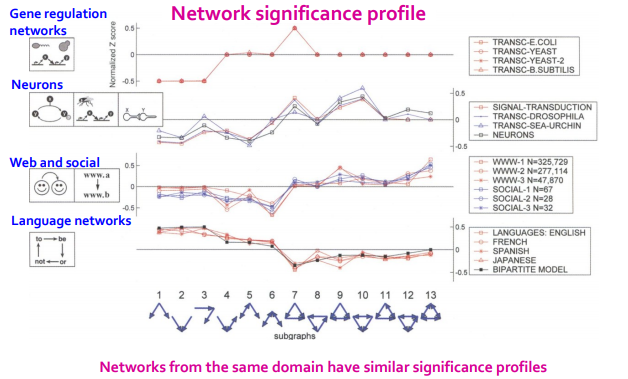
0보다 크면 over-represented, 0보다 작으면 under-represented
network 에 따라 각 subgraph의 significance 는 다르다 ~
(ex. 1번 subgraph : language network 에서는 significance 크지만 다른 네트워크에서는 under-represented)

2. Motifs & Graphlets

Network Motifs

Network Motifs : recurring, significant patterns of interconnections

Network Motifs는, 다음 요소로 정의된다 ~

• pattern : small induced subgraph 에서 발견
  (induced = if you have a set of nodes, then you take all the edges between that set of nodes)
  subgraph가 유도될 수 있는 패턴
• recurring : frequency, 발생 빈도
• significant : 랜덤으로 발생시킨 네트워크보다 더 많이 발생

motifs를 통해 network가 어떻게 구성되고 작동하는지 알 수 있다 ~

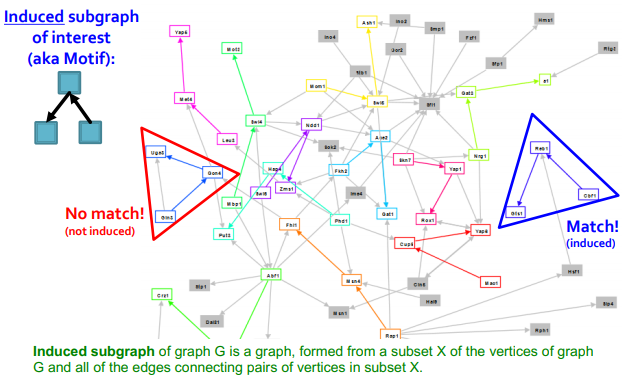
pattern : 빨간색이 not matched 인 이유는 회색 선 때문...
빨간색의 subgraph는 내가 가지고 있는 pattern에 존재하지 않기 때문에 induced(유도)되지 못한다구 함..

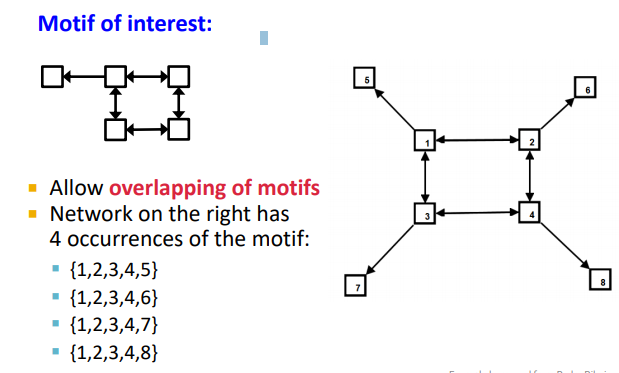
recurring : 51234, 62431, 73124, 84312 처럼 4번 overlap 되어 나타난다 ~

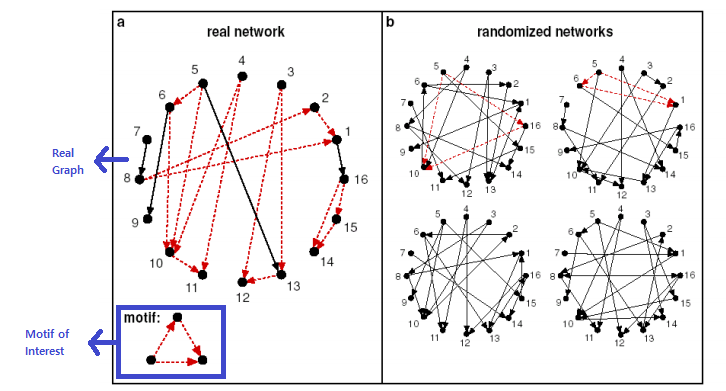
significance : 파란색 네모가 random network 보다 real network 에서 훨씬 고빈도로 나타남 ~

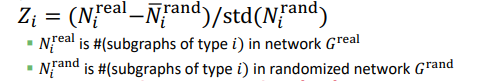
Z-score 로 계산하고,

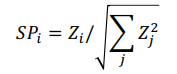
(SP) normalize 한다 ~

학생 질문 🙋🏻‍♀️ : significance 왜 계산해요 ~ ?

답변 👨🏻‍🏫 : 정보를 abstract 해 주기 위해서용 ~
큰 네트워크일수록 instance가 많아지기 때문에, significance 값이 점점 더 커집니다
그래서 normalize 함으로써, dense를 측정해여
(절대적인 수치보다는 normalize 하는 것이 더 유의미)

Configuration Model

null model이 되는 random graph 만들기!

1. Spoke

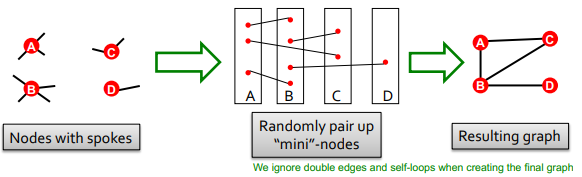
1. Nodes with spokes : 각 node 에 대해 degree 지정
2. randomly pair-up mini-nodes : degree 개수에 맞게 연결
3. resulting graph : 완성 ~
   (1번 degree랑 실제 그래프 degree 다르게 보이는 것 주의!)

spoke 방법론으로는 double edge, self-loof 를 고려하지 못한다는 단점이 존재한다

2. Switching

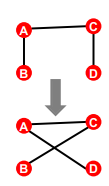
1. A→B, C→D 처럼 랜덤으로 pair of edge 설정
2. endpoint 바꾸기! A→D, C→B
3. randomly rewire 하면서, converge 할 때 까지 반복 ~

교체(swap)하게 되면 degree sequence 철저하게 준수 가능하지만, rewire 방법은 spoke방법론에 비해 매우 느리다는 단점이 있다

Detecting Motifs

Z-score 통해서 network motif에서의 중요 subgraph pick!
일반적으로 10,000 ~ 100,000 개의 random subgraph를 만든다구 한다.. ㄷㄷ

Graphlets

graphlets : connected non-isomorphic subgraphs

• motif : 전체 network 특징화
• graphlet : 주어진 node 특징화

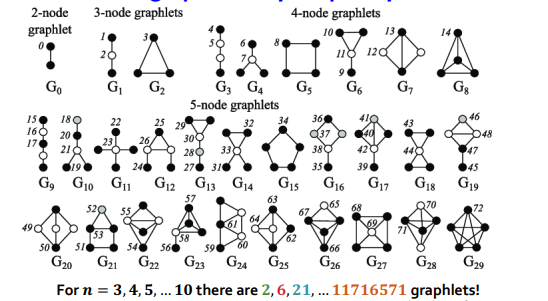
graphlet을 통해 node-level subgraph metric을 얻을 수 있다 ~

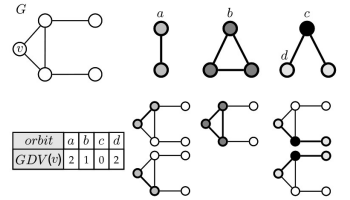
• automorphism orbit : takes into account the symmetries of a subgraph
• Graphlet Degree Vector (GDV) : 각 orbit position에서 node의 빈도에 대한 벡터

그래서 이걸 어떻게 계산하는지 체크해 보면 ~
1. 기준 : G 그래프에 있는 v, 이를 기준으로 GDV 구한다
2. a를 v 위치에 넣어서 개수를 세고, b를 v 위치에 넣어서 개수를 세고, ...
3. c가 0인 이유는, v 자리에 넣었을 때 해당 graphlet이 존재할 수 없기 때문 (선이 연결되어 있기 때문에 b 모양이 생김..)

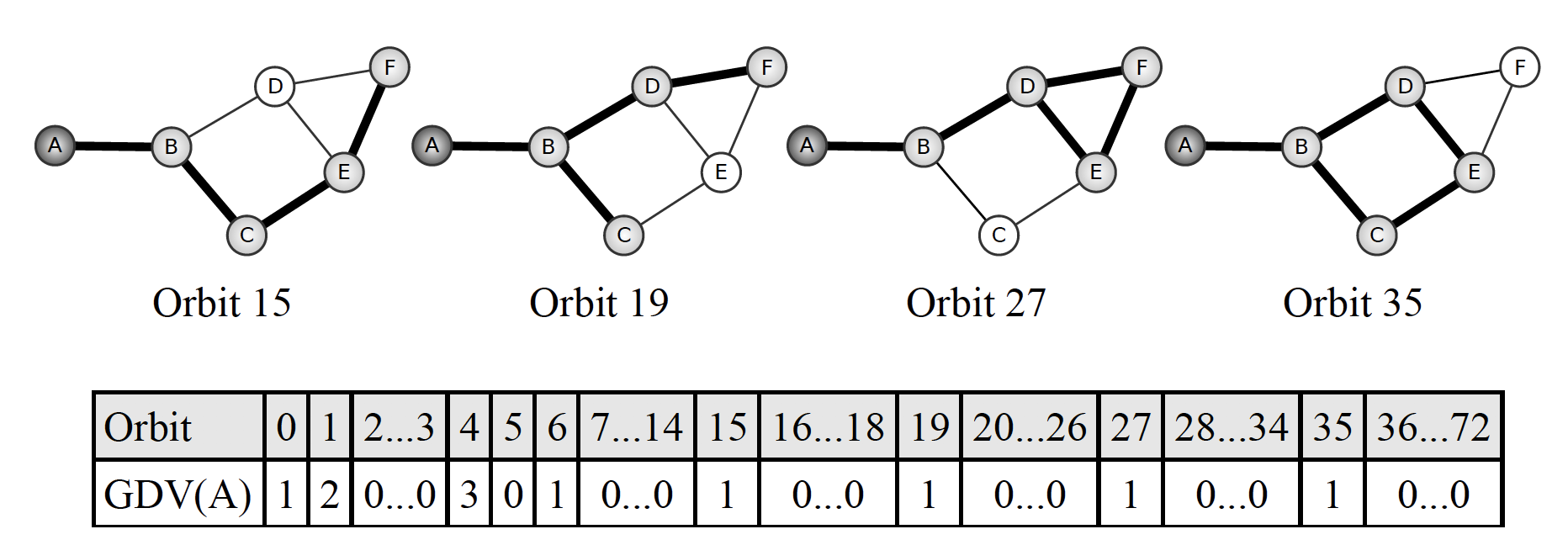
GDV는 하나의 노드를 기준으로 73개의 차원으로 구성된 벡터 (두 개 위의 graphlet 그림에서 graphlet이 0~72 여서 73개임..ㄷㄷ) + graphlet 실제 개수는 훨씬 많으니깐, 네트워크의 node/edge 개수에 따라 차원이 달라지지 않을까 생각 ㅎㅎ...
이 벡터를 가지고 노드를 특징화 할 수 있으며 다양하게 활용해 볼 수 있다 ~

+ (내가 이해한) Motif vs Graphlet

Finding Motifs and Graphlets

size-k의 motifs/graphlets을 그냥 무작정 찾으면...
1. Enumerating : 모든 k 의 subgraph 고려 (find all the instances)
2. counting : 모든 subgraph 개수 세기 (count all of them together)
라는 hard computation problem 이 발생하게 된다

따라서 ESU algorithm 을 통해 exact subgraph 를 찾는다 ~

Exact Subgraph Enumeration (ESU)

• node v로 시작, 정점의 집합에 다른 정점 집합들을 추가해 나가는 방법
• recursive algorithm
• ESU-Tree : tree-like structure of depth k

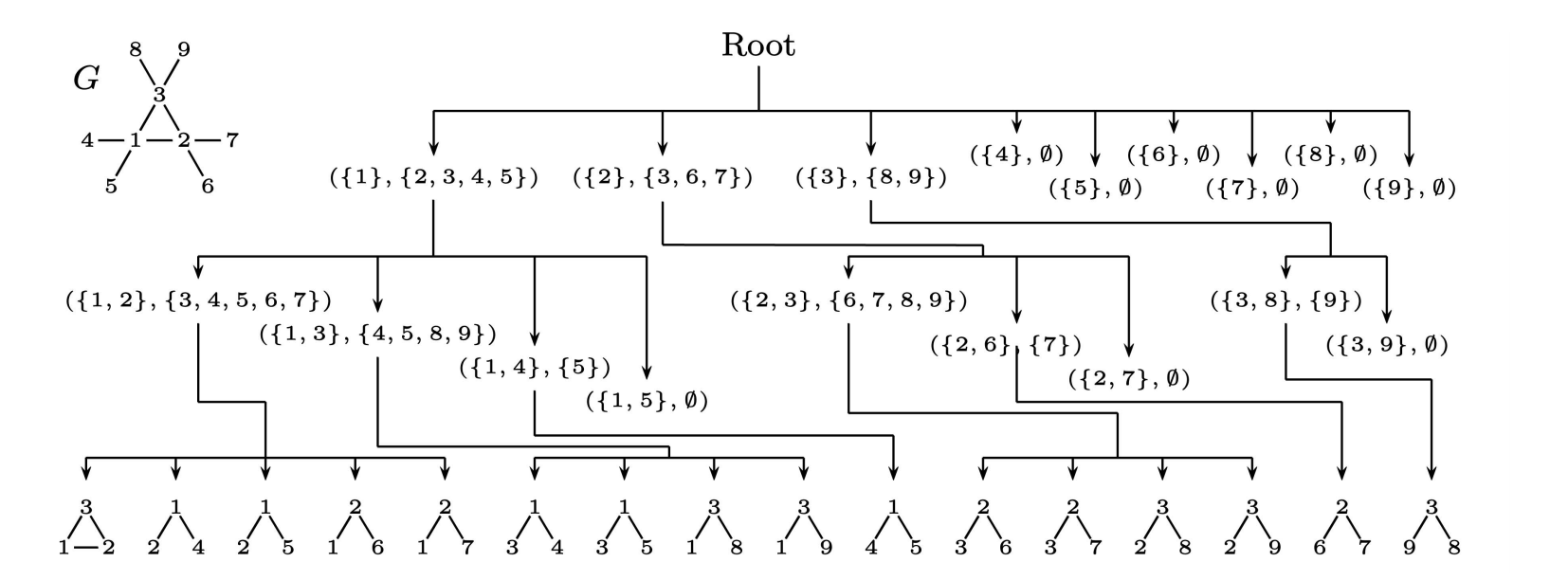
1. {$V_{subgraph}$, $V_{extension}$} 으로 구성
2. $V_{extension}$은 $V_{subgraph}$ 보다 커야 함 ~
3. size=k 되면 terminate
4. 가장 최종 노드 = induced subgraph

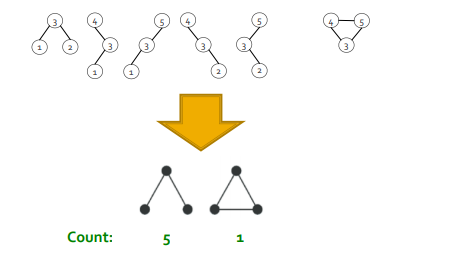
이걸 통해 동형 그래프 개수를 count 한다 ~
isomorphic 한 그래프 끼리는 한 그룹으로 묶는다

topologically equivalent 한지 판별하는 과정 또한 필요한데, 이는 McKay's nauty algorithm을 사용한다고 한다

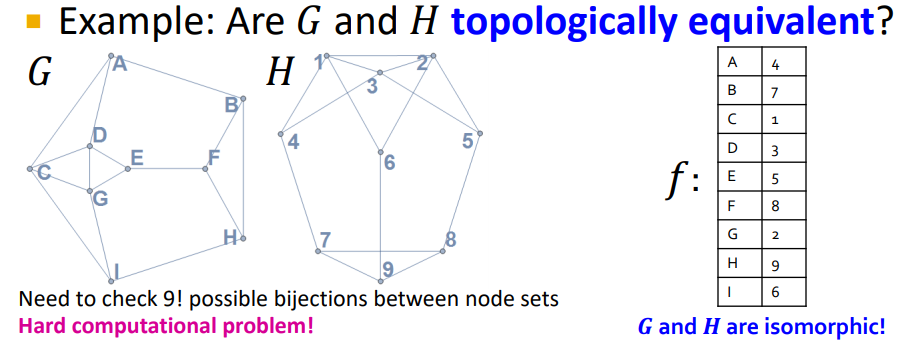
Bijection f:V(G) → V(H)가 존재하면 그래프 G와 H는 Isomorphic하다
그래프 G의 두 노드 u와 v가 adjacent <=> 그래프 H에서 f(u)와 f(v)가 adjacent
(= mapping directly in line)
→ G와 H는 isomorphic (topologically equivalent)!

3. Role & Applications

Role

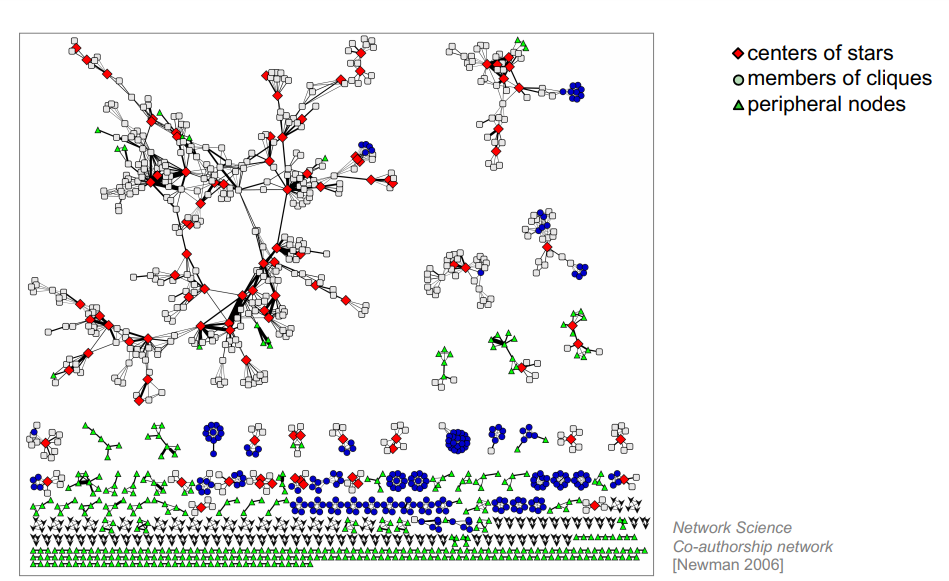
네트워크 상에서 노드들의 역할
Role : A collection of nodes which have similar positions in a network

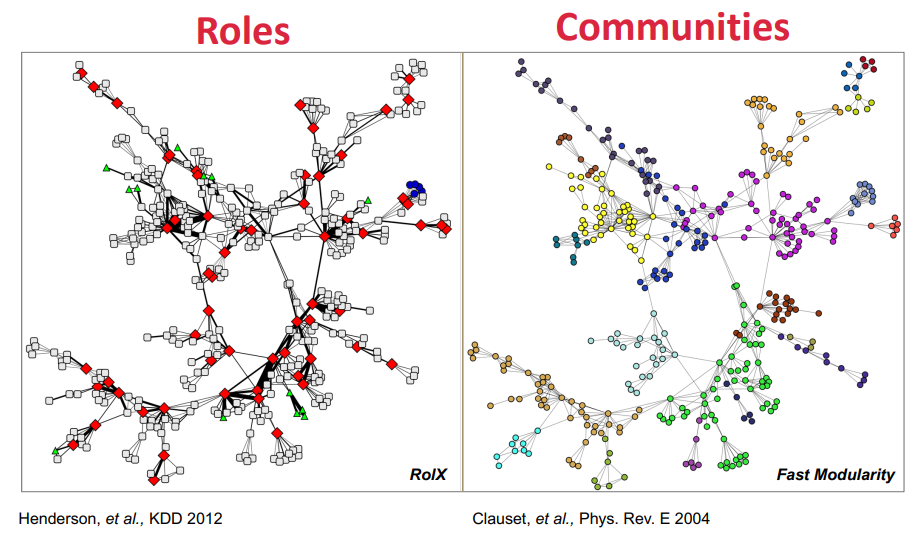
Role 과 Community 는 다르다 ~

• Role : 네트워크에서 유사한 역할을 하는 노드들의 집합
  ex. faculty, student, staff, ...
• community : 네트워크에서 잘 연결되어 있는 group
  ex. AI lab, Info lab, Theory lab, ...

그리고 이 둘은 상호 보완적인 역할을 함...

Structural Equivalence

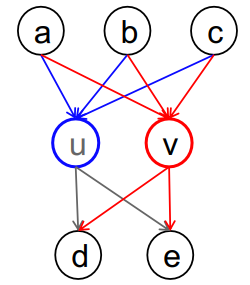
노드 u와 노드 v가 다른 노드들 사이의 관계가 동등하다면 u와 v는 structural equivalence

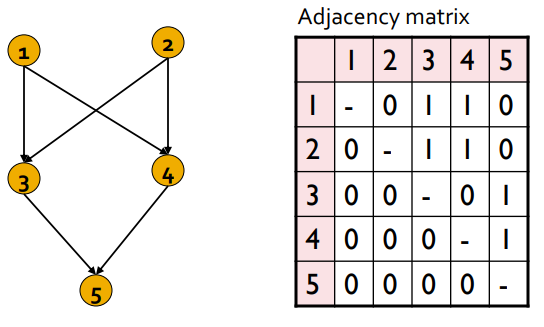
discover it by using clustering

RolX

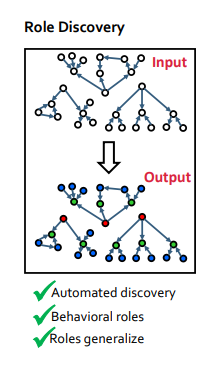
RolX : Network에서 노드들의 Structural Roles를 발견하는 automatic한 방법

• 비지도 학습 방법
• Prior Knowledge 필요하지 않음
• 각 노드에 role들의 mixed-membership 할당 (role을 하나로 국한해서 정하지 않고, 함축적인 의미로 정함 ex. roleA 95%, roleB 5%)

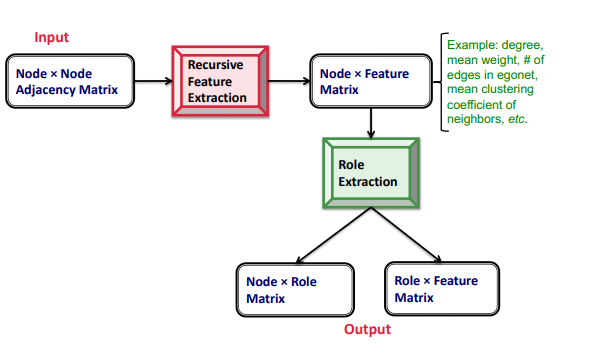
1. node x node 인접행렬을 구하고
2. recursive feature extraction 을 통해 node x feature 로 만들기
3. 여기서 node x role , role x feature 로 분해!
   (matrix factorization 생각이 났음......)

recursive feature extraction

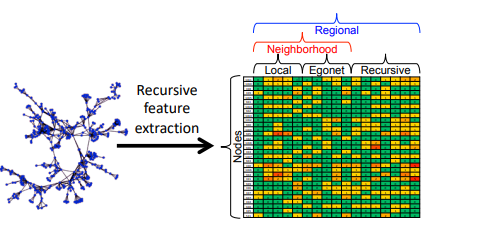
재귀적으로 돌면서 feature를 만들어낸다 ~
local : 해당 노드 정보 / egonet : 이웃 차수까지 고려한 정보
정보들 (= local network에 대한 정보 + neighborhood 정보 + node와의 연결성에 대한 정보) 결합해서 (mean, sum 같은 통계량 만들고 여기서 또 통계량 만들고 또 통계량 만들고 ... 이런식으로 계속 재귀적으로 반복하며 수많은) feature를 만들어낸다
너무 많이 만들면 계산해야 할 양이 많아지기 때문에 pruning 한다구 함..

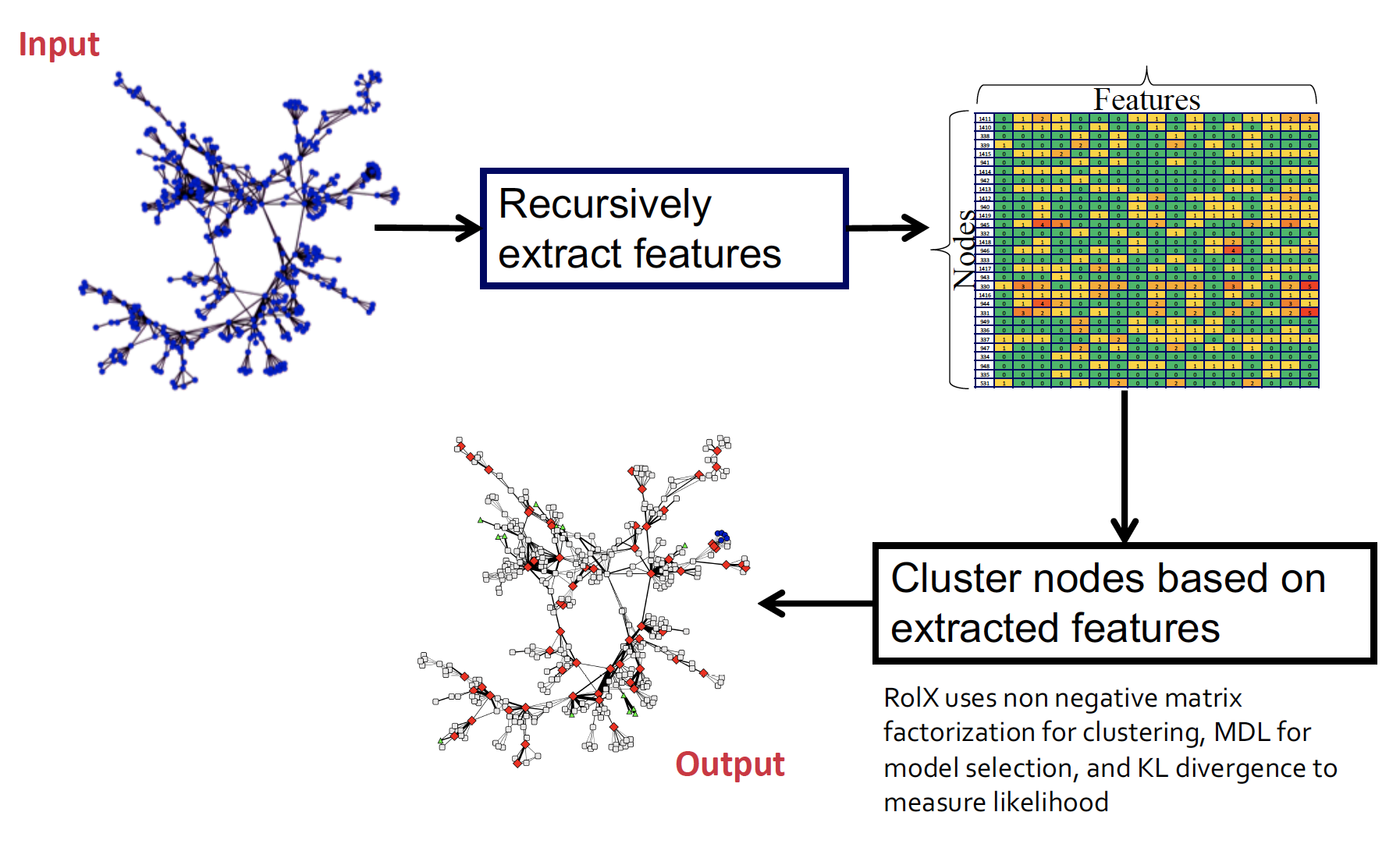
이걸 통해서 나온 extracted features를 통해 clustering 을 할 수 있게 되는데,
이 때 clustering 은 similarity 나 k-means 등등의 방법론으로 진행한다고 한다
이를 통해 clustering 된 output 생성 ~

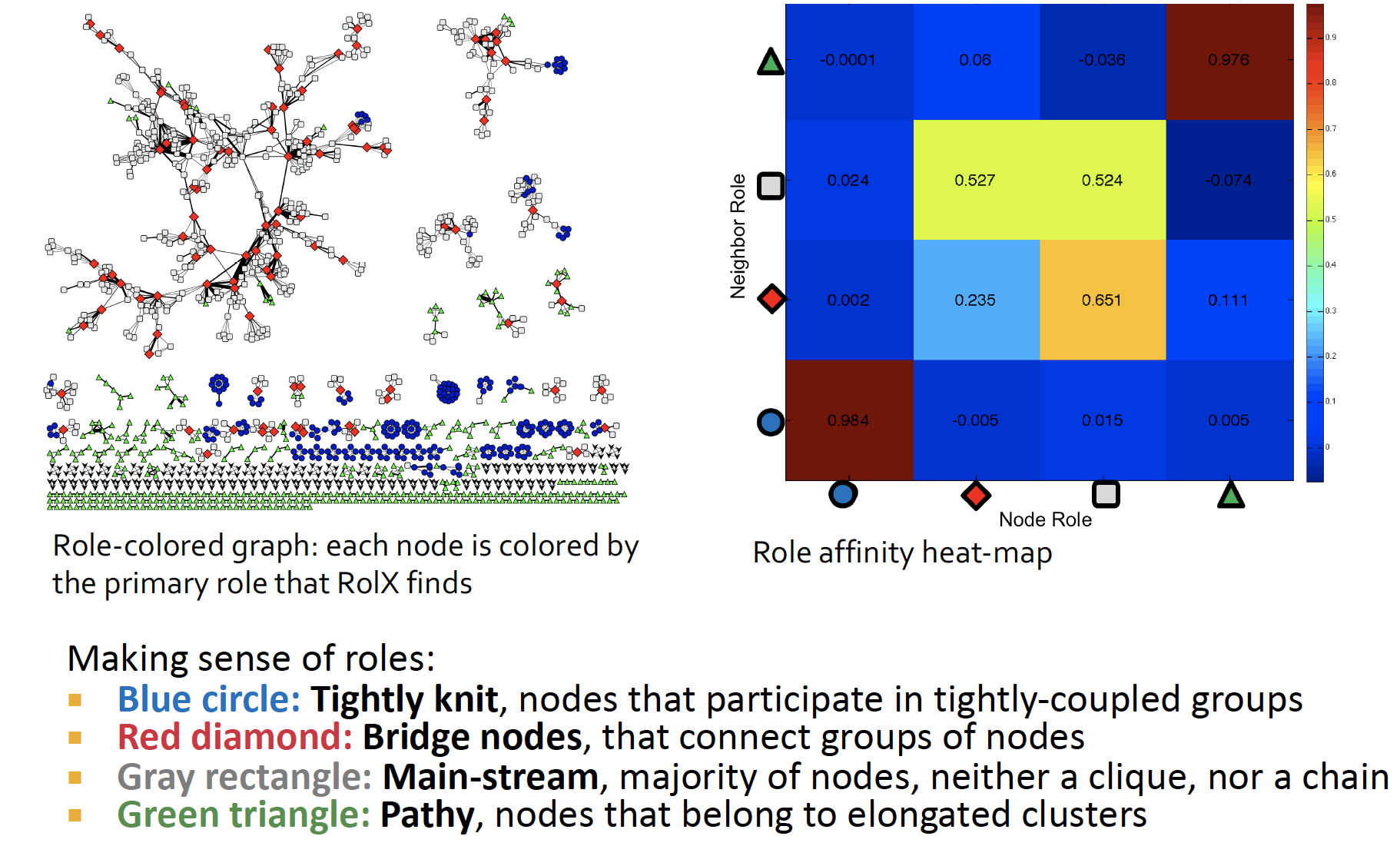
상관계수를 통해서, 각각 node들의 role이 어떤 역할을 하는지 알 수 있다

role distribution 을 통해 두 네트워크 사이의 구조적인 유사도를 비교할 수 있다고 함 ~

Reference

1. 똑똑이 진석이의 띵강 & 벨로그 리뷰
2. 12기 갓승현 3강 리뷰

---

3. 데이터 괴짜님 Review : CS224W - 03.Motifs and Structural Roles in Networks
   
4. 이현준님 Review : cs224w 3강 정리( Motifs and Structural Roles in Networks)