Linear Algebra 내용이 가득가득한 5강 ~ 이해하고 작성하는 데 백만년 걸림 😇

Contents

1. Graph Partition
2. Spectral Clustering
3. Motif-Based Spectral Clustering

1. Graph Partition

Graph Cut

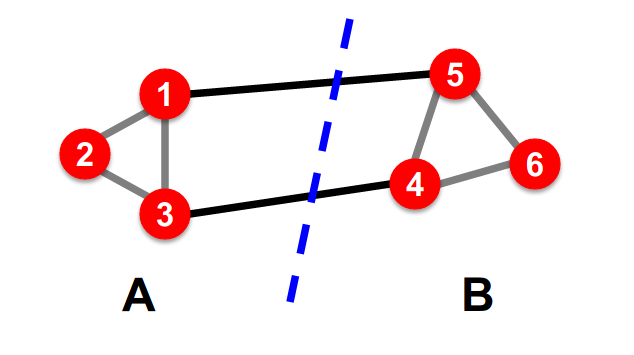
Bi-Partitioning Task : graph를 두 그룹으로 나누는 것

좋은 partition은 무엇일까 ~?
→ 그룹 내의 connection 최대화 & 그룹 간의 connection 최소화 (개수)

통계 표본론이 생각났는데.. 층화추출로 표본을 뽑을 때 (거리)

• cluster 내부는 동질적으로 표본을 뽑고 (homogeneous)
• cluster 간에는 이질적으로 표본을 뽑는다 (heterogeneous)

그래프에서는 두 그룹을 나누기 위해... cut 이라는 개념이 도입되는데,

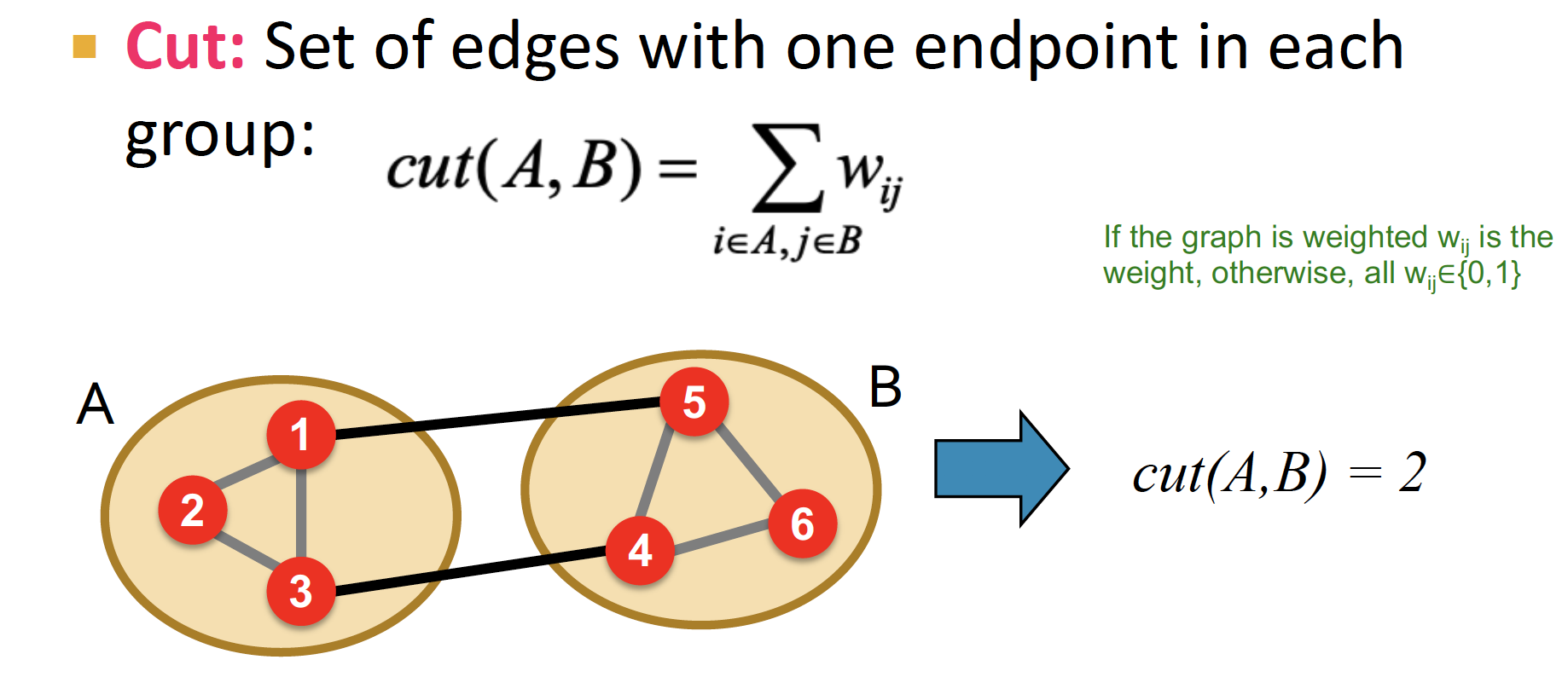
cut : 두 개의 Sets를 얻기 위해 끊어야 하는 edge의 개수
= 한 group에서 다른 group으로 가는 edge들의 가중치 합
(그림에서는 1→5, 3→4 두 개라서 cut(A,B) = 2)

Graph Cut Criterion

1. Minimum Cut

cut 값만을 최소화 하는 방향으로 두 그룹을 쪼개게 되면, external cluster connection 만 고려하기 때문에 제대로 나누지 못하는 문제가 발생한다 ~
(그림에서 optimal cut = 2 이지만, minimum cut = 1)

2. Conductance

Conductance : 각 그룹의 Density 대비 그룹간의 connectivity
conductance를 이용하면 approximately balanced 한 partition을 얻을 수 있다
$\because$ vol(A), vol(B)를 고려해서 값을 계산하게 되는데, 각 그룹의 size가 비슷해 질 수록 min(vol(A), vol(B)) 값은 커지게 되므고, $\phi$ 값은 작아진다

하지만 이렇게 계산하는 것 역시 hard computation problem 존재... (NP-hard)

그래서 고유값과 고유벡터를 이용해서 partition 하는 방법론을 찾게 되고... 그것 땜시 선대를 엄청 공부하게 되는...결과를 낳게 된다...ㅎㅅㅎ...

Spectral Graph Theory

$A \cdot x$ 의 의미는 ~?
$y_i$ = node i에 연결되어 있는 것 다 더한 값!
($A$ : adj matrix, $x_i$ : value of node i)

고유값(eigenvalue) & 고유벡터(eigenvector) 정의
정방행렬 A에 대하여 Ax = λx (상수 λ) 가 성립하는 0이 아닌 벡터 x가 존재할 때, 상수 λ 를 행렬 A의 고유값 (eigenvalue), x 를 이에 대응하는 고유벡터 (eigenvector) 라고 한다

고유값과 고유벡터의 기하학적 의미

• 벡터 x에 대해, n차 정방행렬 A를 곱하는 결과 = 상수 λ를 곱하는 결과
• 행렬의 곱의 결과가 원래 벡터와 방향은 같고, 배율만 상수 λ 만큼만 비례해서 변했다는 의미
• 행렬과 벡터 곱을 수행할 때 방향도 바뀌고 크기(배율) 도 모두 바뀌는 것 (=Ax) 보다는, 방향은 유지하며 크기(배율) 만 바뀌는 것 (=λx) 이 훨씬 연산이 간단할 것 ~

Spectrum : eigenvalue들을 오름차순으로 정렬했을 때, 이에 상응하는 eigenvector들을 의미
그래프 G를 나타내는 함수의 Spectrum을 분석하는 것이 Spectral Graph Theory

Case 1. d-Regular Graph

d-regular : 모든 node가 동일한 degree 값 d를 가지는 connected 그래프 G

모든 node의 degree=d 라면, $y_i$ 는 sum of labels 이기 때문에,
Ax=(d,d,...,d)가 될 것 ~

이 때 고유값 분해 (Ax = λx)를 생각해 보았을 때,
우리는 {x=(1,1,...,1), λ=d} 라는 서로 상응하는 one pair 를 찾을 수 있다
추가로, d가 A의 eigenvalue들 중 가장 큰 값이다!

~ 증명 ~
Theorem
Let $G$ be a connected graph, the eigenvalue of $G$ of largest absolute is the maximum degree iff $G$ is regular

Proof
$x_j$ : $\underset{i}{max}|x_i|$
$|\lambda||x_j|$ = $|(Ax)_{j}|$ = $|\sum_{V \in N(V_j)} x_i|$ $\leq$ deg $v_j |x_j|$ $\leq$ $d \cdot |x_j|$
$\therefore$ $|\lambda| \leq d$

Case 2. Graph on 2 Components

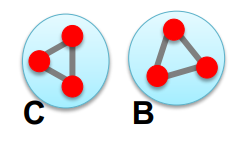
그래프가 연결되어 있지 않고, d-regular 2개 그래프로 나뉘어 있는 경우!

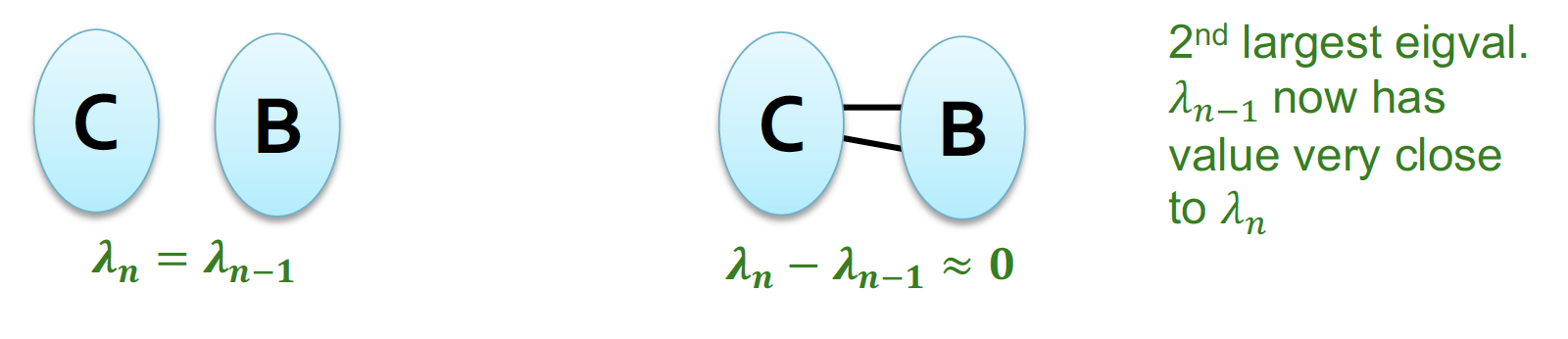
두 번째로 큰 eigenvalue(=$\lambda_{n-1}$) 에 대응되는 eigenvector(=$x_{n-1}$)가 양수인 node와 음수인 node에 따라서 두 component를 구분할 수 있다

여기 부분 차근차근 증명 정리해 봄 ~

1. Eigenvectors are orthogonal

대칭행렬에 대해서는 eigenvector들이 서로 orthogonal 하다!

• 직교행렬 (Orthogonal Matrix)
  • 행렬과 행렬의 전치행렬을 곱하면 단위행렬이 되는 경우
  • $AA'$ = $A'A$ = $I$ → $A^{-1}$ = $A'$
• 대칭행렬 (Symmatrix Matrix)
  • 정방행렬 중에서 대각원소를 중심으로 원소 값들이 대칭되는 행렬
    (우리가 undirected graph 에서 계속 보고 있는 인접행렬 ~) → $A$ = $A'$
  • 대칭행렬은 항상 고유값 대각화가 가능하며 직교행렬로 대각화가 가능하다!
  • $A$ = $P\Lambda P^{-1}$ = $P\Lambda P'$, $PP'$ = $I$

$A$는 symmetric matrix 이며,
$Au_{1}$ = $\lambda_1 u_{1}$, $Au_{2}$ = $\lambda_2 u_{2}$ 를 만족하는 $\lambda_1$, $\lambda_2$ 존재한다고 할 때,

$Au_{1}$ = $\lambda_1 u_{1}$ 에서 양 변에 ${u_{2}}'$ 를 곱하면
$\lambda_1 \cdot {u_{2}}' \cdot u_{1}$ = ${u_{2}}' \cdot Au_{1}$ = ${(Au_{2})}' \cdot u_{1}$ = ${(\lambda_2 u_{2})}' \cdot u_{1}$ = $\lambda_2 \cdot {u_{2}}' \cdot u_{1}$

즉, $\lambda_1 \cdot {u_{2}}' \cdot u_{1}$ = $\lambda_2 \cdot {u_{2}}' \cdot u_{1}$ 이므로 $(\lambda_2 - \lambda_1) {u_{2}}' u_{1} = 0$
→ $\lambda_1 \neq \lambda_2$ 이므로, ${u_{2}}' u_{1} = 0$

$\therefore$ eigenvectors are orthogonal in symmetric matrix

2. so then the components of $x_{n-1}$ must sum to 0

d-regular graph 에서 n번째(=가장 큰) eigenvalue 값이 d 임을 증명했고, 이 때 상응하는 eigenvector는 $x_n = (1,1,...,1)$ 임을 알고 있다 ~

바로 위에서 대칭행렬에서의 eigenvector 끼리는 서로 독립임을 증명했기 때문에, $x_n \cdot x_{n-1} = 0$ 이 된다!

따라서,
$\sum_{i} {x_n[i] \cdot x_{n-1}[i]}$
= $x_n(1) \cdot x_{n-1}(1)$ + $x_n(2) \cdot x_{n-1}(2)$ + ... + $x_n(k) \cdot x_{n-1}(k)$ = 0 이 되고,
$x_n = (1,1,...,1)$ 이므로, $x_n(1) = x_n(2) = ... = x_n(k) = 1$
이를 대입하면 위의 식은 $\sum_{i} {x_{n-1}[i]} = 0$ 으로 바뀐다 ~

3. $x_{n-1}$ splits the nodes into two groups

$x_{n-1}$ eigenvector 에서, 값들을 다 합쳐서 0이 되어야 하므로 양수/음수 값들이 존재!
따라서 이를 통해 양수 부분과 음수 부분, 두 부분으로 Partition 한다 ~
$x_{n-1}[i] > 0$ vs $x_{n-1}[i] < 0$

그리고 $x_{n-1}$ eigenvector 값 기준으로 나누는 것이므로, 이에 상응하는 $\lambda_{n-1}$ 기준으로, 즉 2번째로 큰 eigenvalue 값을 기준으로 partition을 진행한다 ~

Matrix Representation

Laplacian Matrix

• Adjacency matrix (A) : 인접행렬
• Degree matrix (D) : 대각행렬, node의 degree 값들이 대각원소 값

Laplacian Matrix (L) : Degree - Adjacency

• 대각원소 값 (degree)은 양수 & edge 값 (adj)은 음수
• 하나의 행/열 값을 다 더하면 0!
• 그래서 $x=(1,1,...,1)$ 이라는 eigenvector에 대하여,
  $Lx = 0$ 이 되므로, 이에 대응하는 eigenvalue $\lambda = \lambda_1 = 0$ 이 된다 ~

about Laplacian Matrix

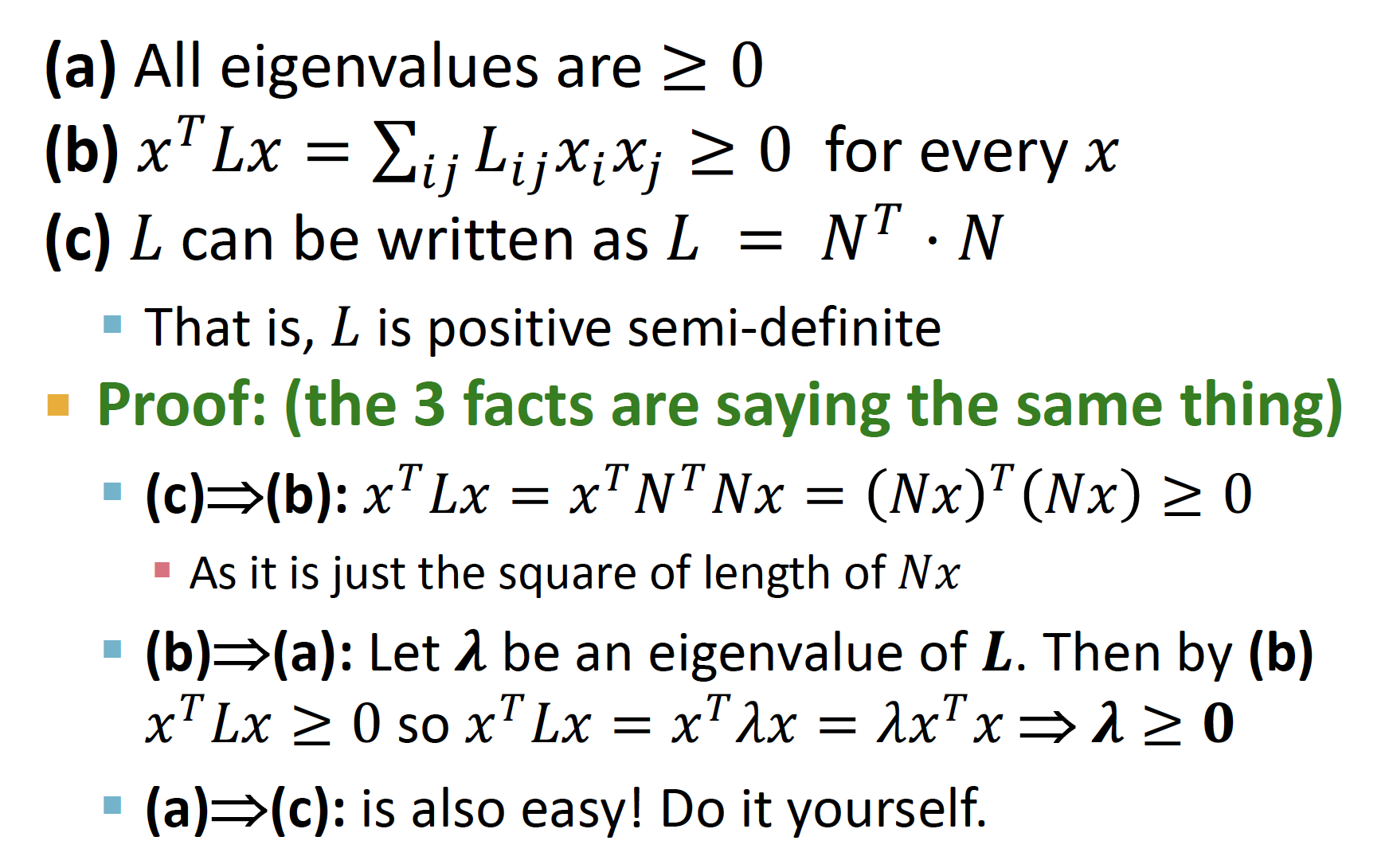
(a) L의 모든 eigenvalue 값은 0보다 크거나 같다
(b) L은 semi-positive definite matrix 이다 (positive definite matrix : 양정치행렬)
(c) L이 양정치행렬이면, $L=N'N$을 만족하는 정칙행렬 $N$ 존재한다

$\lambda_2$ Optimization Problem

Laplacian Matrix의 2번째 eigenvalue를 통해, 그래프를 partition 한다 ~

해당 식을 통해 $\lambda_2$를 찾고, 이에 대응되는 $x_2$에서 양수/음수 값으로 partition 을 분류하는 과정을 거친다! (위의 process와 매우 유사)

위의 증명에 의해, $\underset{v \neq 0}{min}\frac{x'Mx}{x'x}$ 를 만족하는 $x$는 $\lambda_1$(=가장 작은 고유값) 에 대응되는 eigenvector (=$x_1$)

$\underset{x : x'w_1 = 0}{min}\frac{x'Mx}{x'x}$ 식을 해석해 보면,
$x_1$과 수직인 vector 중에서 (=다른 eigenvector 중에서), 가장 작은 값을 찾는 것이므로
이에 해당하는 값은 $\lambda_2$(=2번째로 작은 고유값)에 대응되는 eigenvector (=$x_2$) 이다 ~

분자의 의미는, 값을 차례대로 대입해서 전개해보면 차이 제곱 합 임을 알 수 있다

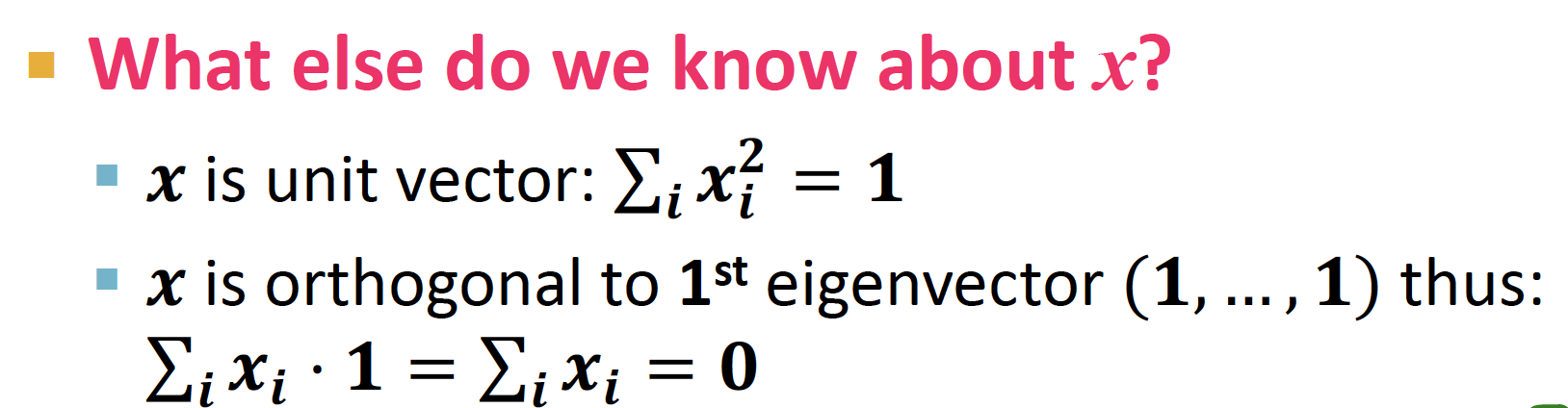
분모의 의미는 unit vector (단위벡터) = 제곱합 1, 다 더하면 0

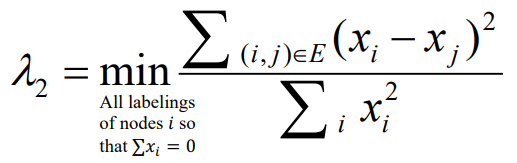
따라서 식을 정리해 보면 위와 같이 정리됨을 알 수 있다!

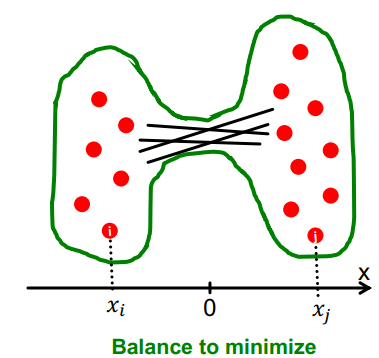
즉, 2번째로 작은 eigenvector에서, 0보다 작은 값은 왼쪽으로, 0보다 큰 값은 오른쪽으로 모아서 partitioning!

Find Optimal Cut

우리의 목표는 A와 B를 잘 나누는 가장 좋은 방법을 찾는 것 ~

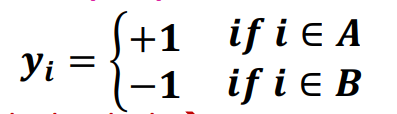
(SVM 처럼) A에 속하는 노드를 +1, B에 속하는 노드를 -1로 둔다

enforce $|A| = |B|$ → $\sum_{i} {y_i} = 0$
$\because$ 합이 0이 되어야 하므로, A의 절댓값(양수 값의 개수)과 B의 절댓값(음수 값의 개수) 같다고 둔다

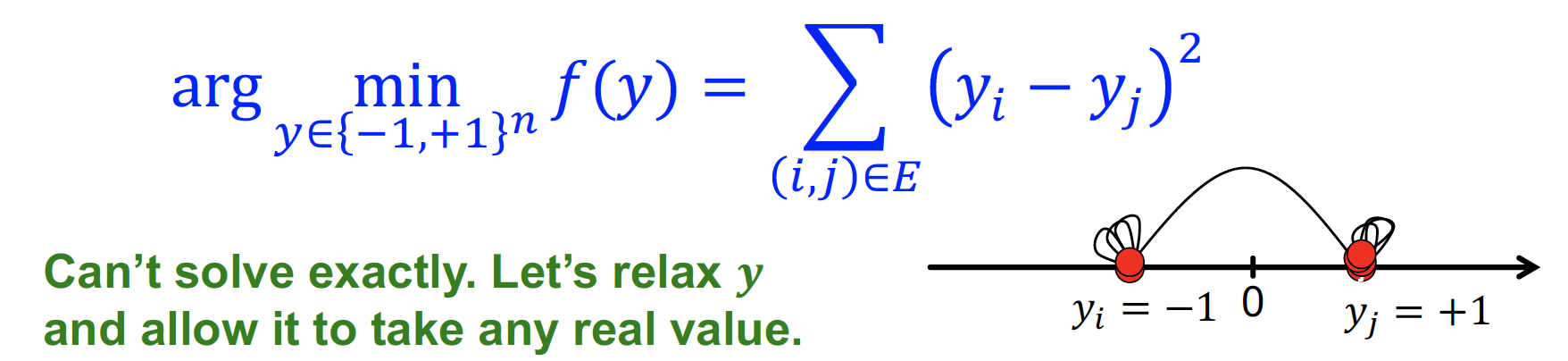
파란색 식 = A와 B cross 하는 edge만 체크한다 ~

Rayleigh Theorem

$\lambda_2$는 위의 식에 대해 optimal solution이고, 이 때 상응하는 eigenvector($x_2$)를 Fiedler vector 라고 한다

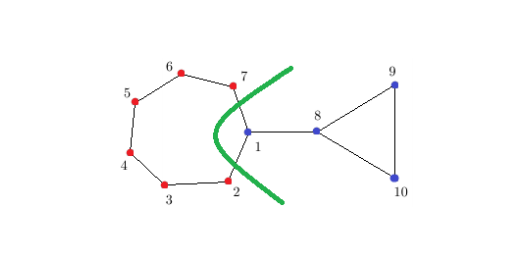
그래서 위의 과정으로 partition 하면 이렇게 됨 ~

Approx. Guarantee of Spectral

(A,B)의 conductance 값을 $\beta$라고 했을 때, 2번째 eigenvalue 값은 $2\beta$를 넘을 수 없다고 한다

증명! b>a 이므로 $\lambda_2 \leq 2\beta$ 식이 성립

여기에 추가적으로, The Cheeger inequality 를 통해 한 번에 $\lambda_2$ 의 lower & upper bound를 설정하는데...

$\frac{\beta^2}{2k_{max}} \leq \lambda_2 \leq 2\beta$ 라고 한다 ~ (증명 수업에서도 생략했구 .. 지쳐서 안 찾아봄..ㅎㅎ)
$\lambda_2$ 는 conductance 에 따라 범위가 설정된다 ~

✨ 결론 ✨
solving $\lambda_2$ = minimize sum of squares of differences

2. Spectral Clustering

Spectral Partitioning Algorithm

위의 내용을 쭉 ~ 그림으로 좀 더 와닿게 다시 표현해 보면 ~

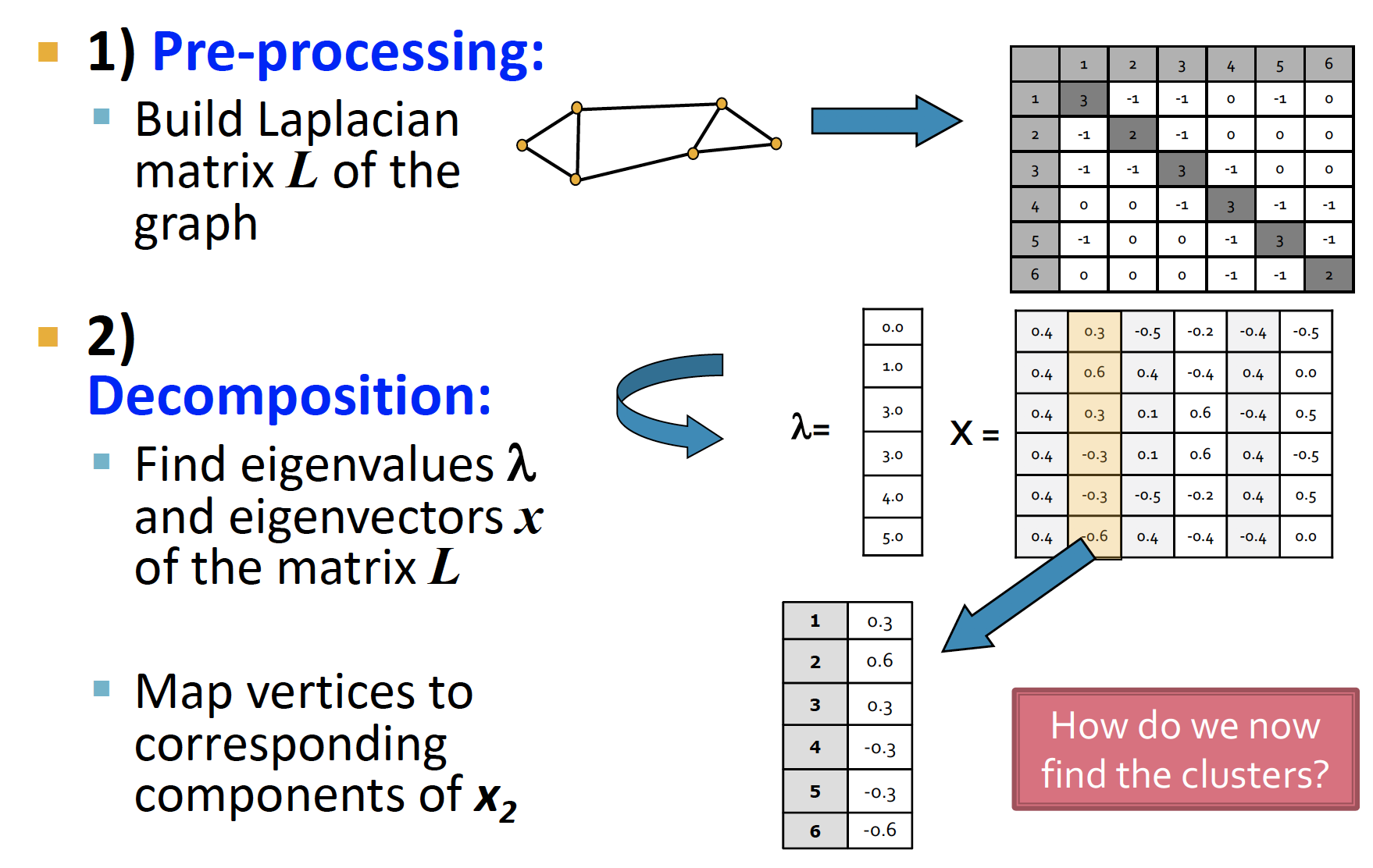
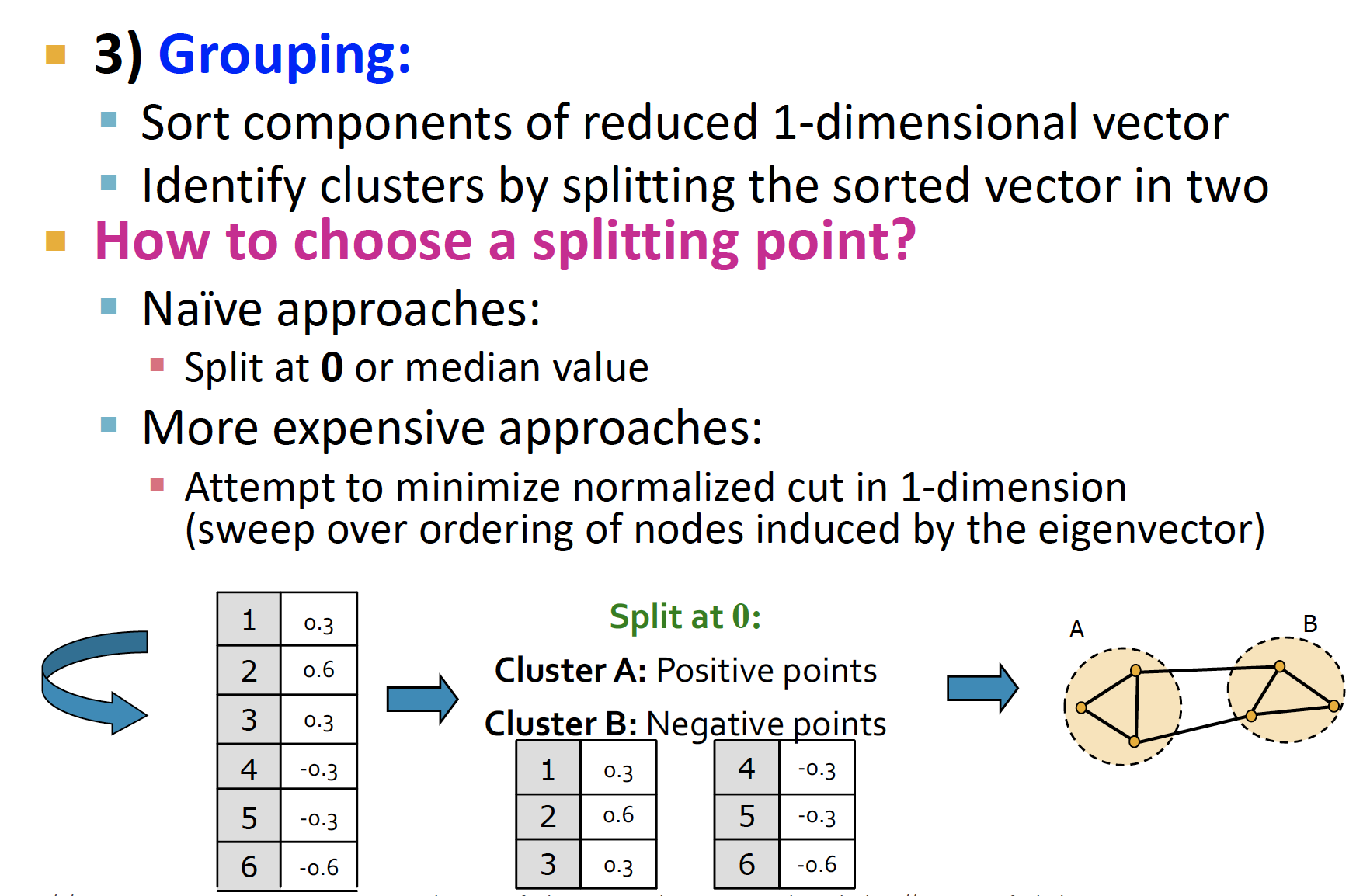
1. Pre-processing : Laplacian Matrix L 생성
2. Decomposition : $Lx = \lambda x$, $\lambda_2$에 상응하는 $x_2$ 찾기
3. Grouping : $x_2$에 있는 node들에 대해, split 기준을 잡아 clustering

k-way Spectral Clustering

위의 그림처럼.. 딱 봐도 2개로 나누는 것 보다 4개로 나누는 게 더 좋아 보일 때는 어떻게 할까 ~

1. Recursive bi-partitioning

위에서 진행했던 두 개로 쪼개는 과정을 재귀적으로 반복한다!
비효율적이고, 불안정적임.. ㅎㅎ

2. Cluster multiple eigenvectors

$\lambda_2$ 만 이용하지 말구, $\lambda_3, \lambda_4, \lambda_5$, ... 살펴보면서 추세를 살펴본다 ~

위의 그림이 $\lambda_3$를 이용해서 clustering 한 결과물! 4개로 잘 쪼개지는 것을 볼 수 있다 ~
($x_1$ components에 대한 그림에서의 conductance가 일직선인 이유는 $\lambda_1$ 에서의 eigenvector의 Sum of Squares = 1 이기 때문..)

k는 위와 같이, eigengap 이 최대가 되는 지점으로 정한다 ~
(k-means 에서 군집 개수 k 설정할 때 elbow point 에서 설정하듯이 설정..)

3. Motif-Based Spectral Clustering

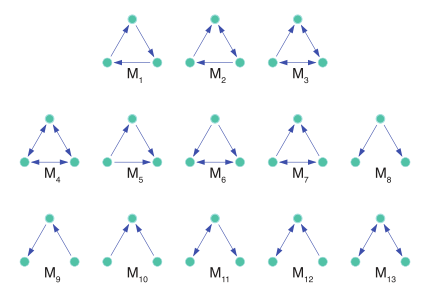
우리는 지금까지 node 기준으로 clustering 하는 방법론을 공부했는데, 그래프에서 관심 있는 pattern을 반영한 (=subgraph) motif를 기준으로 clustering을 하고 싶다면 ~?

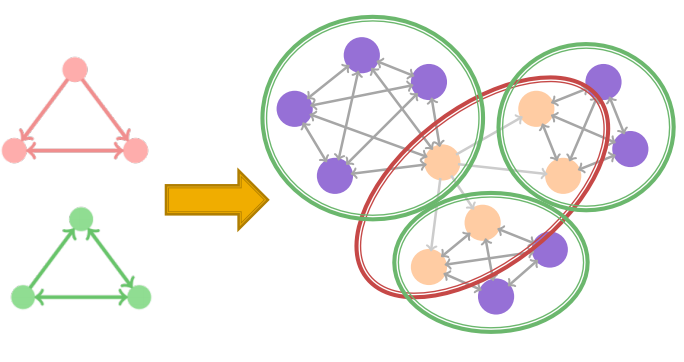
각 motif 들은 각기 다른 modular structure를 나타낸다는 것이 핵심 idea ~

Motif Conductance

node 기준으로 나눌 때 vol & conductance 값을 설정했듯이,
motif 기준으로 나눌 때에도 똑같이 vol & conductance 값을 고려해 나눈다!

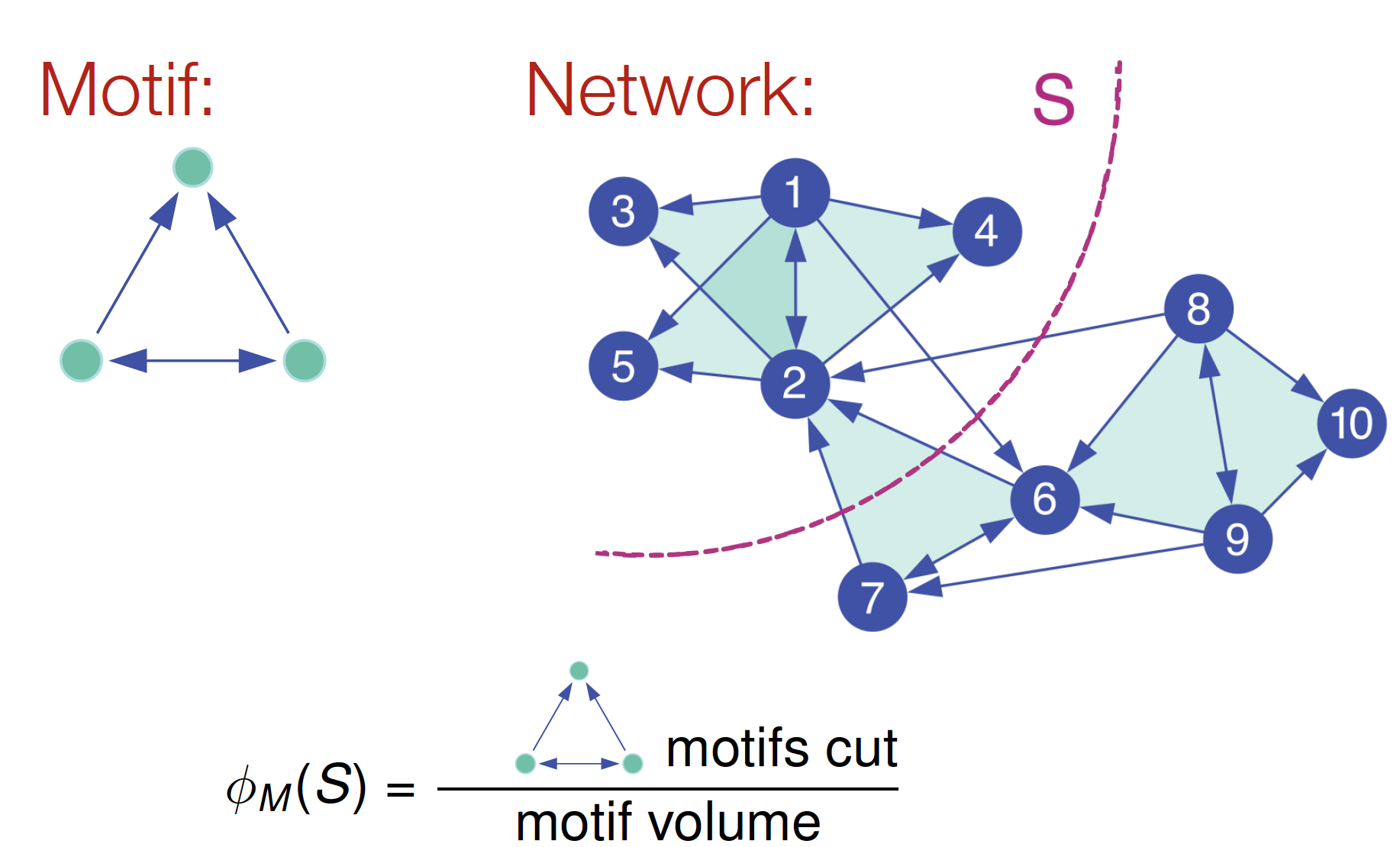
$\phi_M(S)$ = 1/10 인데,
(분모) S에 속하는 instance 개수 = node 12345에 도착하는 edge의 개수 = 10
(분자) 기준이 되는 motif 를 끊은 개수 = 1

근데 이렇게 conductance 계산 하나하나 해서 하는 것 역시 NP-hard computation problem 이 발생한다구 함 ㅎㅎ..

Motif Spectral Clustering

위에서 공부했던 Spectral Clustering 방법론을 적용한다 ~

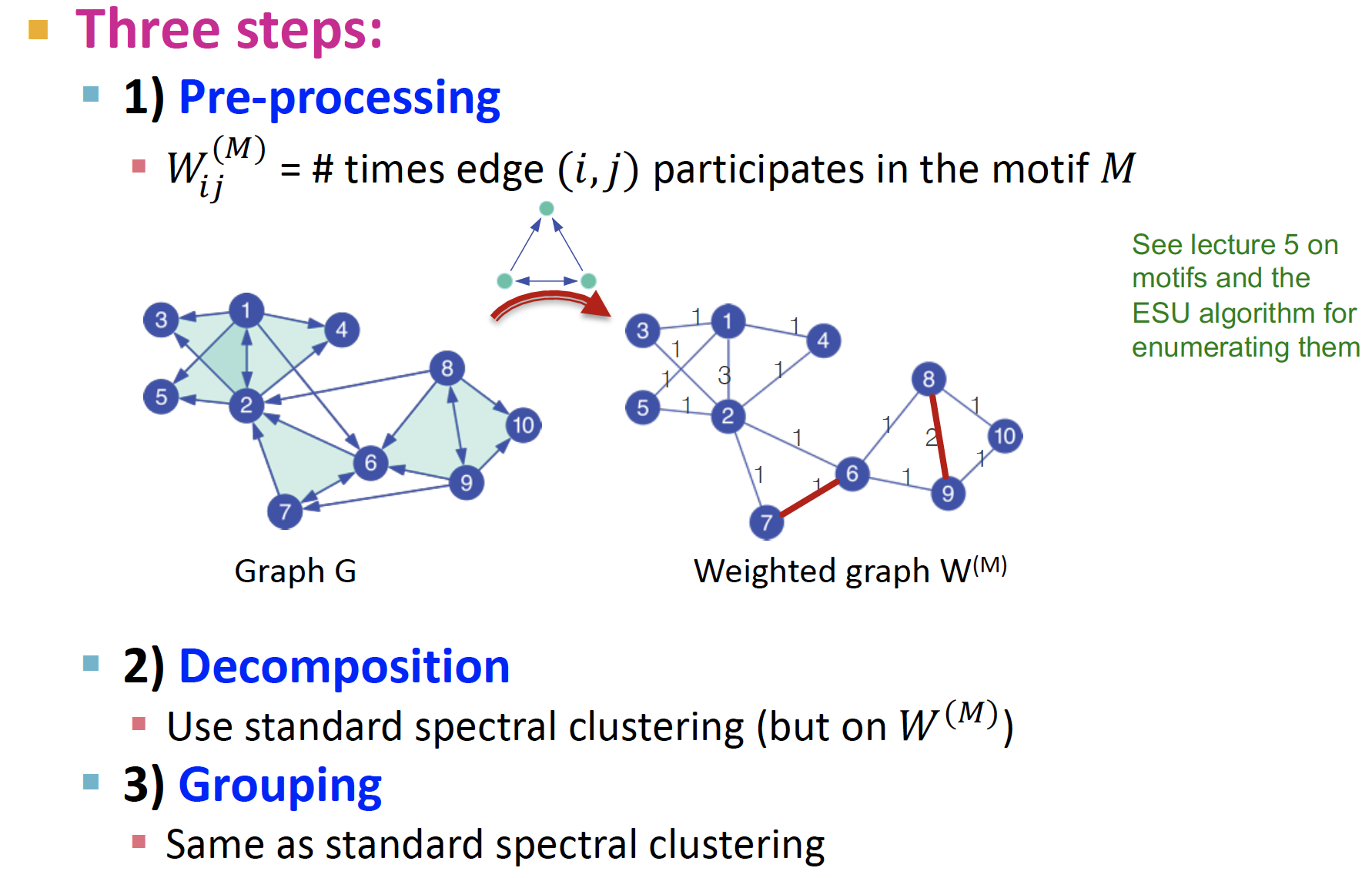
Step 1. Pre-processing

그래프 $G$에서 motif에 대한 weight를 적용한 인접행렬 $W^{(M)}$을 만든다
node 1-2, node8-9 사이의 edge 값의 가중치가 변한 것을 볼 수 있다!

Step 2. Decomposition

1. Weighted graph에 대한 Laplacian Matrix를 만든다
   $L^{(M)} = D^{(M)} - W^{(M)}$
2. eigenvalue decomposition
   $L^{(M)}x = \lambda_2 x$
3. Fiedler vector $x_2$를 구하고, clustering

Step 3. Grouping (Sweep Procedure)

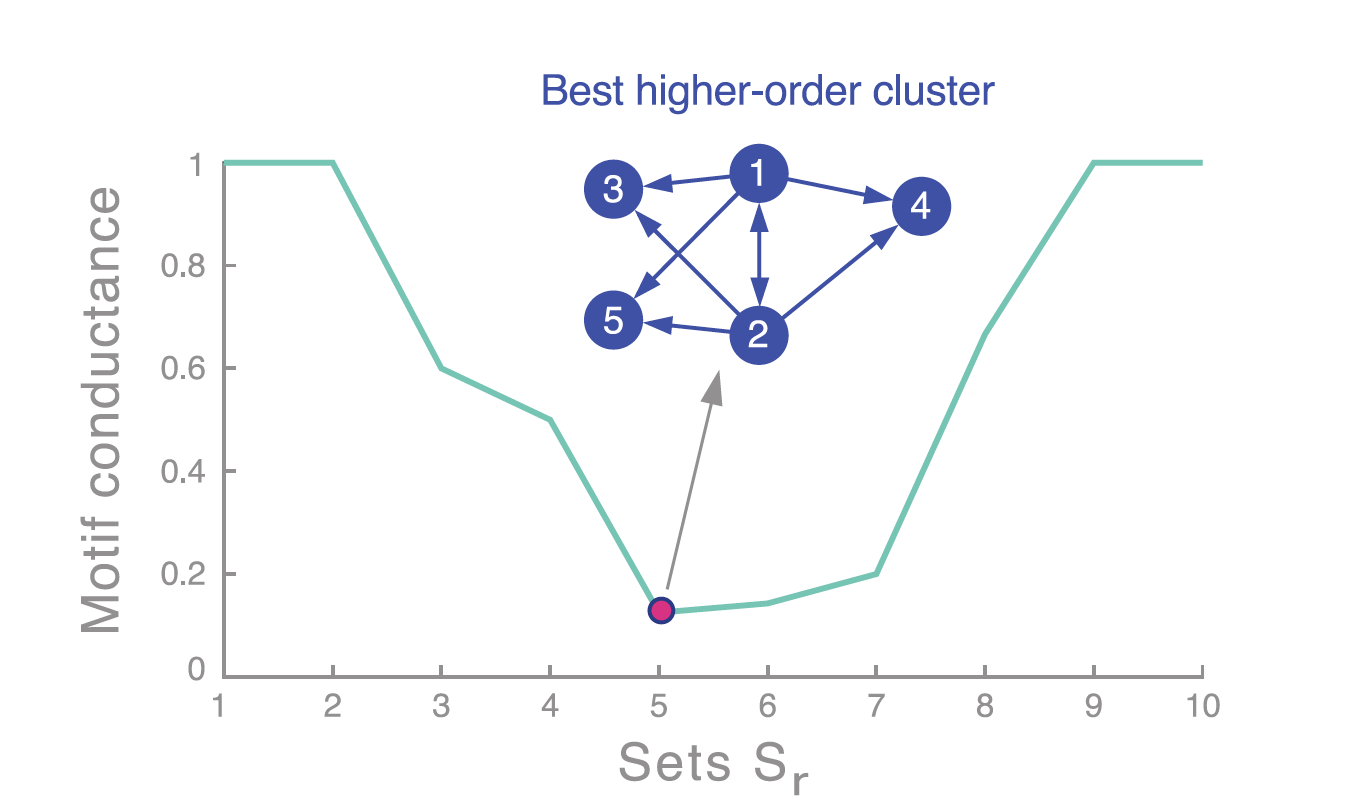
각 eigenvector 로 나눈 값에 대해 conductance 를 계산한 다음에, global minima 가 되는 값으로 cut 값을 설정해 clustering 을 진행한다
(해당 그래프는 convex 한 형태가 아니며, 여기서는 우연히 convex 하게 나왔다구 함)

그리고 계산된 conductance 값은 이렇게 bound 가 설정된다고 한다 ~
(node spectral clustering에서 bound를 설정해 줄 때 봤던, The Cheeger inequality)

Application

해양 생태계에서, 먹이 사슬 구조 기반으로 clustering 하는 데에 관심있다면 ~?

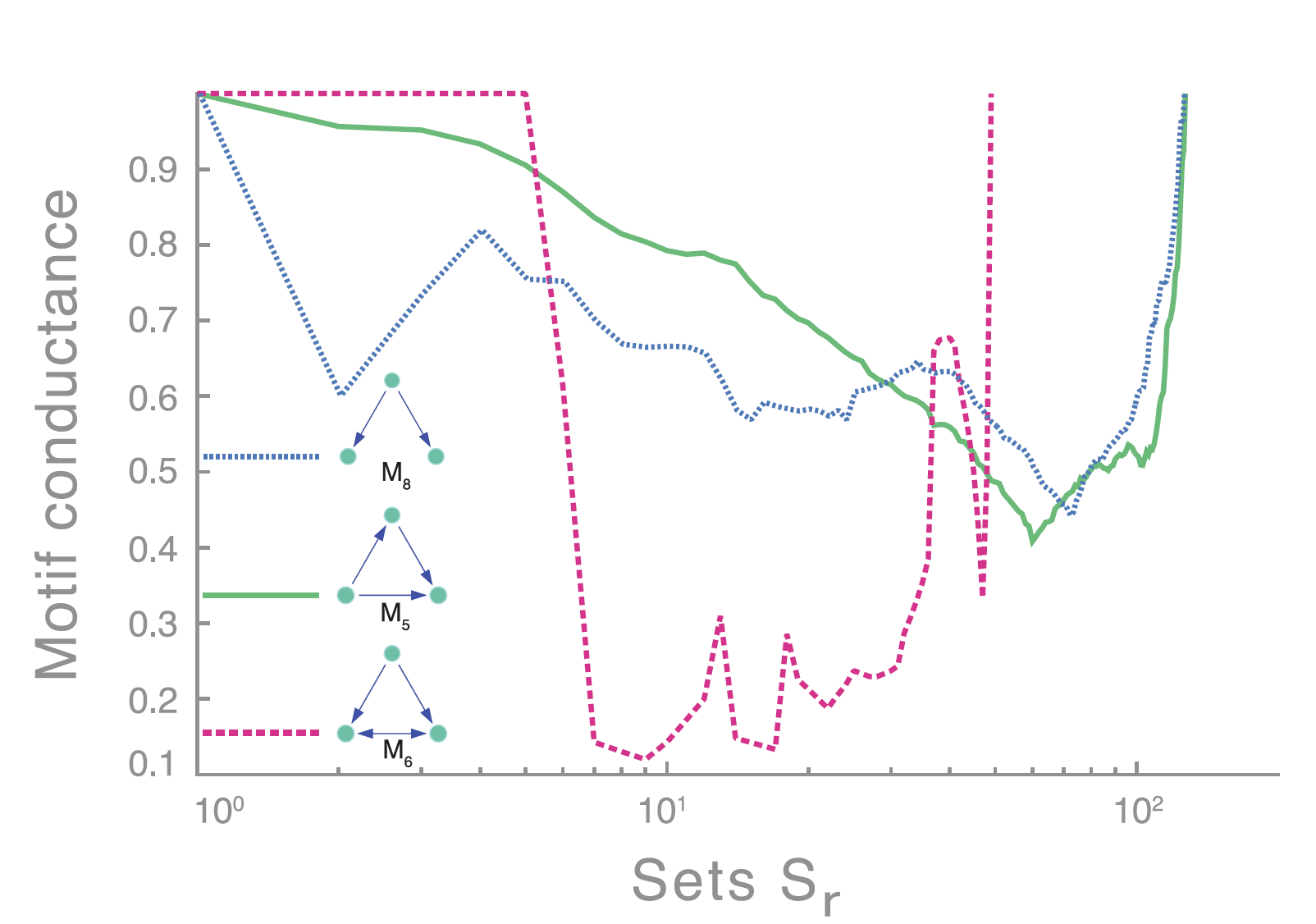
M6 : 아래 두 개 노드는 위의 노드의 food source 인데, 서로의 먹이가 되는.. 요상한 먹이사슬 관계
해당 먹이사슬 관계를 기반으로 motif-based spectral clustering 을 진행해 보면, 다른 motif로 clustering 을 진행할 때 보다 아주 이상적으로 (minimum conductance) 나뉘는 것을 볼 수 있다 ~

매우 이상적인 바닷속 생물들 사이의 관계를 얻을 수 있다!

Reference

1. 컴천 민준이의 띵강 & 벨로그 리뷰
2. 선대 러버 진혁이의 5강 리뷰

---

1. 데이터 괴짜님 Review : CS224W - 05.Spectral Clustering
2. Symmetric matrices
3. CalTech Class Material : Eigenvalues in Regular Graphs
4. Fiedler’s Theory of Spectral Graph Partitioning
5. [선형대수] 고유값(eigenvalue), 고유벡터(eigenvector) 의 정의
6. 투빅스 14기 정규세션 : 혜빈이의 선형대수 추가자료
7. 그 밖의 선형대수 개념 구글링...