Contents
- Network Community
- Modularity
- Overlapping Community
1. Network Community
3강에서는 Roles에 대해 배우고, 이번 4강에서는 Community에 대해 배운다 ~
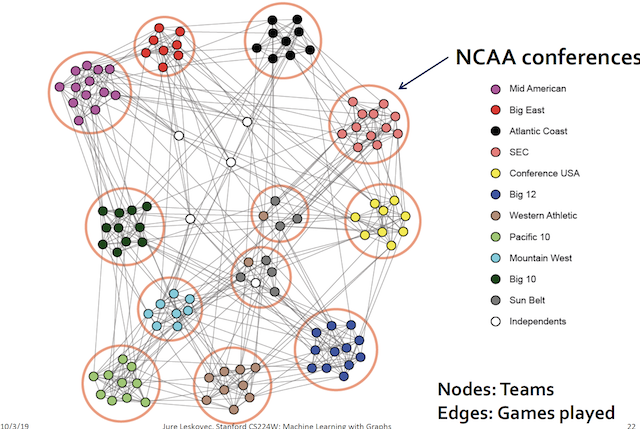
Community : set of tightly connected nodes,
서로간에 밀접하게 (densely) 뭉쳐져 있는 노드의 집합 (cluster)
Intro
흥미로운 사실 🧐 사람들이 new job을 찾을 때, close friend 보다 very rarely meet 하는 acquiantances 들에게서 더 많은 정보를 얻는다고 한다
왜냐면, friendship 에는 두 가지 관점이 있는데,
1. structural : friendship이 network의 어떤 부분을 연결하는지 체크하고
2. interpersonal : friendship이 strong 할 수도 있고 weak 할 수도 있다
Granovetter's Explanation
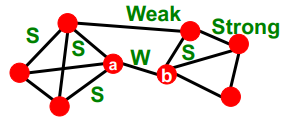
structural- S : embedded edges는 사회적으로 매우 강한 관계를 갖고,
- W : 서로 다른 네트워크를 연결하고 있는 엣지 (long-range edges)는 사회적으로 약한 관계를 갖는다.
information- W : long-range edges를 통해서 새로운 정보 (=다른 part의 network 정보)를 얻을 수 있다
- S : embedded edges를 통해서는 redundant information (불필요하게 과도한 정보) 를 얻게 되는 경향이 있다 ..
| S | W | |
|---|---|---|
| Structure | Socially Strong | Socially Weak |
| Information | Redundant | Useful |
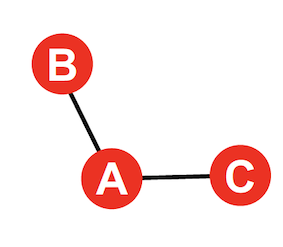
그래서 A를 통해 건너 건너 관계인 B C 가 더 job을 얻기 좋은 관계라고 말 함.. 그래서 nurture your weak ties 라고 하심 ㅋㅋㅋㅋㅋ (약간 어이없구 모르겟음 내가 이해를 제대로 한 게 맞나 ~?)
Edge Overlap
.png)
친구들끼리 얼마나 겹쳐 있는지를 체크하는 수식!
초록색 선분으로 연결된 두 점에 대해서, 파랑과 빨강이 동시에 갖고 있는 노드
- : 2 friends in common out of 6
- : 4 friends in common out of 6
Edge / Link Removal
Edge Removal by Strength, Link Removal by Overlap 모두 Low to High로 끊는 것이 cluster 끼리 더 빨리 떨어진다고 한다 ~
Network Community
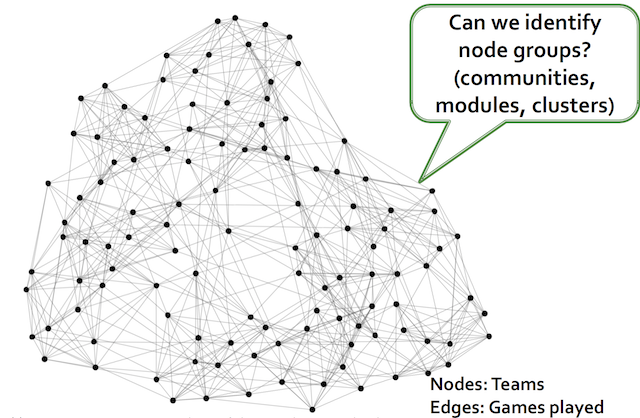
그래서 위와 같은 input 이 들어오게 되면
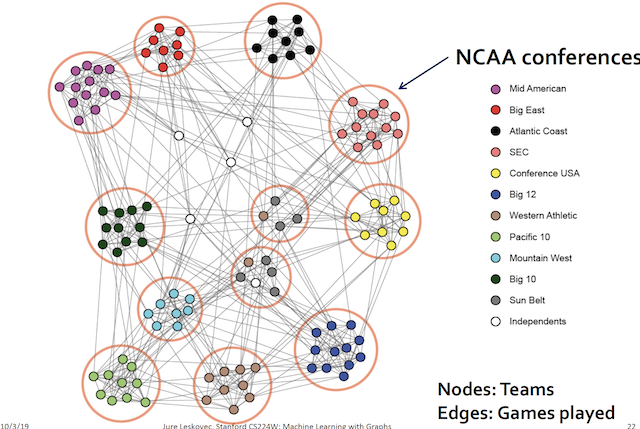
output 은 이런식으로 나온다 ~
2. Modularity
.png)
Modularity Q : network가 community로 얼마나 잘 나누어졌는가 (partitioning) 에 대한 수치
Q = community s의 edge 수 - community s의 edge 기댓값
이 수치가 클수록 (edge 수 차이가 클수록) 우리는 매우 strong group이라고 할 수 있다
기댓값을 구하기 위해서는, null model 을 알아야 함 ~
Null Model : Configuration Model
.png)
n개의 node와 m개의 edge가 있는 그래프 G 에서, edge를 rewire 해서 random graph인 G' network 를 만든다 ~
이 때 node i와 j 사이를 연결하는 edge의 기댓값 =
는 2m개의 node 중에서, target node () 와 연결될 확률을 의미!
(2m인 이유 = every node counted twice)
아래의 식은 위의 기댓값에 대한 식이 맞다는 것을 증명 ~
.png)
- i, j : pair of community
- : expected number of edges
- : normalizing constant
- : indicator function (same group에 속하면 1, 아니면 0)
💡 결론 : we can identify communities by maximizing modularity
negative value 의미 🙋🏻♀️ ?
- identify anti-community
- set of people don't link each other → 서로 연결되어 있지 않은, clustering 제대로 하지 않은 community
- 그럼 이것도 community 예요? No No
- 그럼 0.5 랑 -0.5 의미가 동일한가요? No No
→ dual problem 이 아니어서 동일하지 않아용
Louvain Algorithm
modularity를 maximize 하는 것이 목적!
hierarchy로 community를 찾는다
greedy algorithm 이며 heuristic algorithm 임... ㅎㅎ
시간복잡도는 + n은 # of nodes in the network!
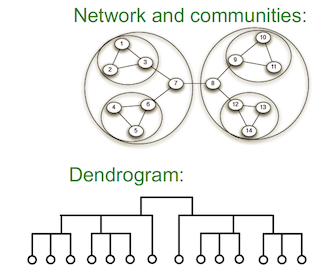
PROCESS
1. 가장 조그만 원끼리 묶고 (123)
2. 그 다음에 큰 원 묶고 (1-7)
3. entire community 묶는다 (1-14)
dendrogram 을 사용해서 hierarchy를 찾는다 ~
매우 빠르고, 수렴도 빠르고, 결과물도 좋다고 (high modularity output) 한다
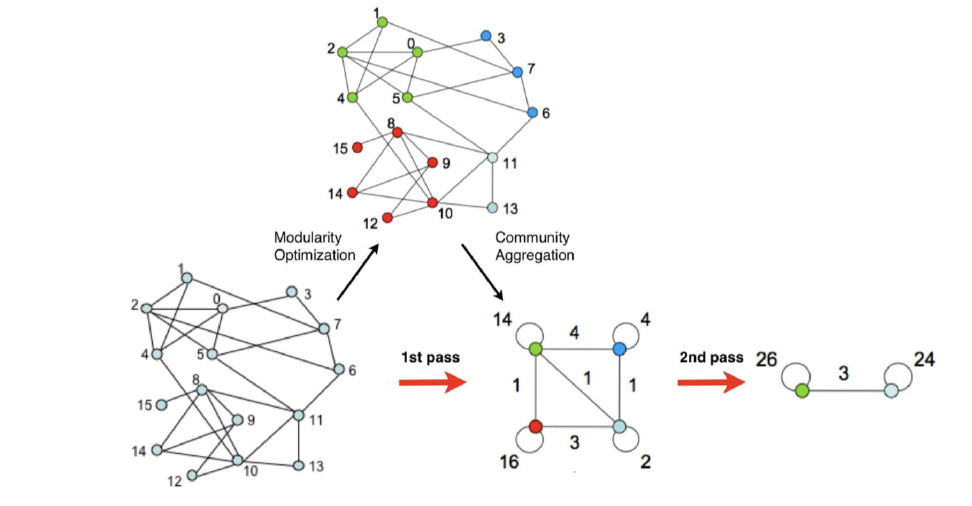
.png)
Phase1 : Modularity Optimization
- Modularity 증가량 () 을 살펴본다!
- node를 community에서 다른 community로 옮겨보고, modularity가 증가하면, 옮긴다 ~
- modularity가 개선되지 않을 때 까지 반복 ~
Phase2 : Community Aggregation
- phase1 에서 찾은 community 를 merge 하여 super node 를 만든다
- phase1 으로 돌아간다 ~
.png)
- : 노드 i를 C community에 추가시켰을 때 Q의 증가량
- : D community 에서 노드i를 제거시켰을 때 Q의 증가량
- = +
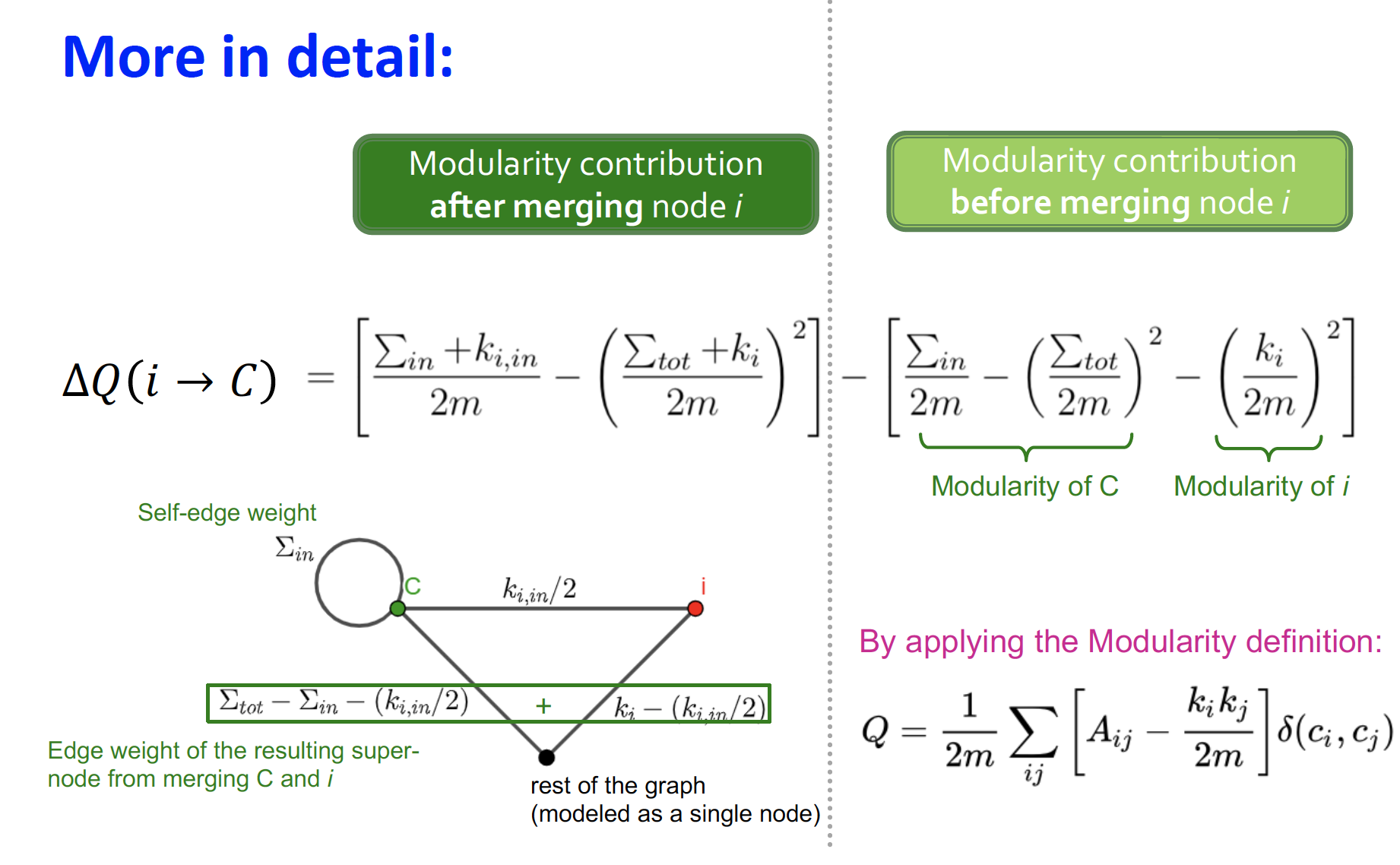
이런식으로 를 계산한다구 함 ...
(빨간색 i = interest)

알고리즘으로 표현하면 위와 같다 ~
example
.png)
- 숫자 : total weight of connections
- 마지막 그림에서.. 26 = 14+4+4+4 / 3 = 1+1+1 / 24 = 16+2+3+3 (두 node 사이를 연결하는 edge 두 번 count)
3. Overlapping Community
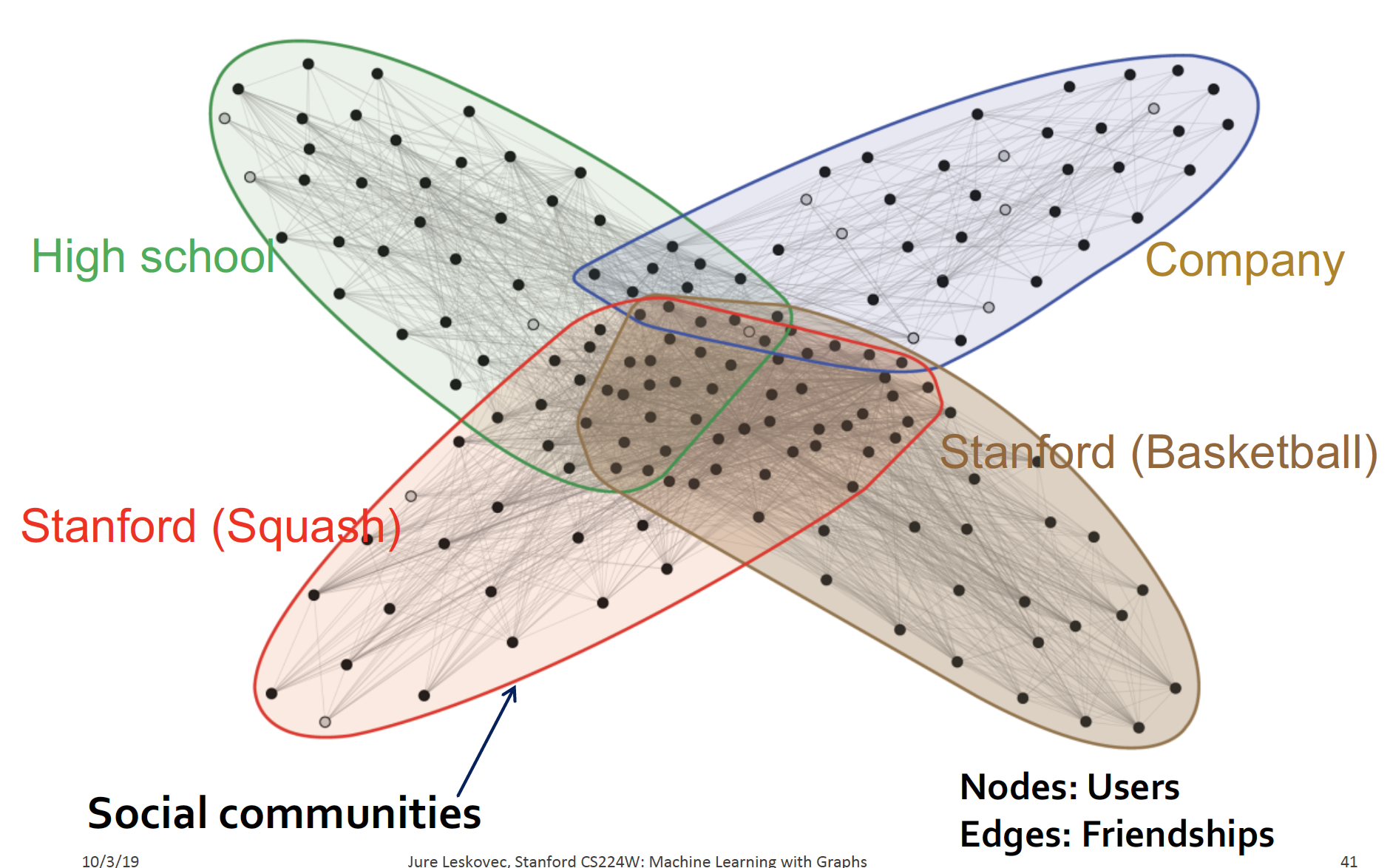
살다보면 마니 마니 겹치게 됨 ~
.png)
인접행렬에서도 이를 확인할 수 있음!
그래서 이런 겹치는 community 들을 어떻게 표현하는가 ...
.png)
Step1 : AGM 정의
Step2 : AGM으로 그래프 G가 generate 되었다고 가정하고, G가 최적 parameter를 가지고 있는 그래프가 되는 AGM을 찾는다 → 그리고 이를 통해 community를 찾는다!
(MLE 찾는 과정이랑 비슷하다고 이해함 ..)
AGM : Community-Affiliation Graph Model
.png)
왼쪽의 그림은 Bipartite Graph!
.png)
- : community c에 속하거나, 속하지 않거나 (성공 확률)
- : u와 v 가 연결될 확률, 두 노드의 공통된 커뮤니티에 속하지 않을 확률을 모두 곱한 뒤(product) 1에서 빼주는 것 (여집합 개념)
Detecting Communities
.png)
주어진 graph (오른쪽) 에서 model F (왼쪽) 어떻게 찾을까 ~?
.png)
- F가 주어졌을 때 : given my model parameters
- G가 나올 확률 : how likely similar as possible as the graph
- 이 값을 최대화 시키는 F를 찾아야 함 ~ (MLE! gradient descent 같은 방법론으로 찾는다)
.png)
P(G|F) : F가 주어졌을 때 G가 나올 확률
- 왼쪽 행렬
제일 처음엔 randomized stochastic 하게 each prob 생성!
each edge generated independently... - 오른쪽 인접행렬 및 아래의 식
(u,v) G : Value 1 / (u,v) G : Value 0
.png)
- : 노드 u가 각각의 커뮤니티에 속할 확률을 가진 벡터
- : 노드 u와 노드v가 각각의 community에 동시에 속할 확률 (하나의 노드라도 어떤 커뮤니티에 속할 확률이 0이라면 둘의 product는 0)
확률 정의를 위해 exponential 함수 등장하는데, 이는 NLP glove embedding 에서 나온 homomorphism 개념을 차용한 것 ~ (괜시리 반가워씀..😇)
- Glove Insight : 임베딩 된
input= 두 단어벡터의 내적이 말뭉치에서의output= 동시 등장확률 로그값 이 되도록 목적함수를 정의 - F(A-B) = F(A)/F(B) 를 만족하는 함수는 지수함수!
그래서 위의 파란 식을 위의 P(G|F)에 넣고 log를 취해 log-likelihood 형태로 만들면,
.png)
이렇게 되고, log-likelihood 값을 최대로 만드는 F를 찾으면 된다 ~
