
🔍 배열 데이터를 효과적으로 다루는 NumPy
- 과학 연산을 쉽고 빠르게 할 수 있게 만든 패키지
- 다차원 배열 데이터를 효과적으로 처리 가능
배열 Array
순서가 있는 같은 종류의 데이터가 저장된 집합
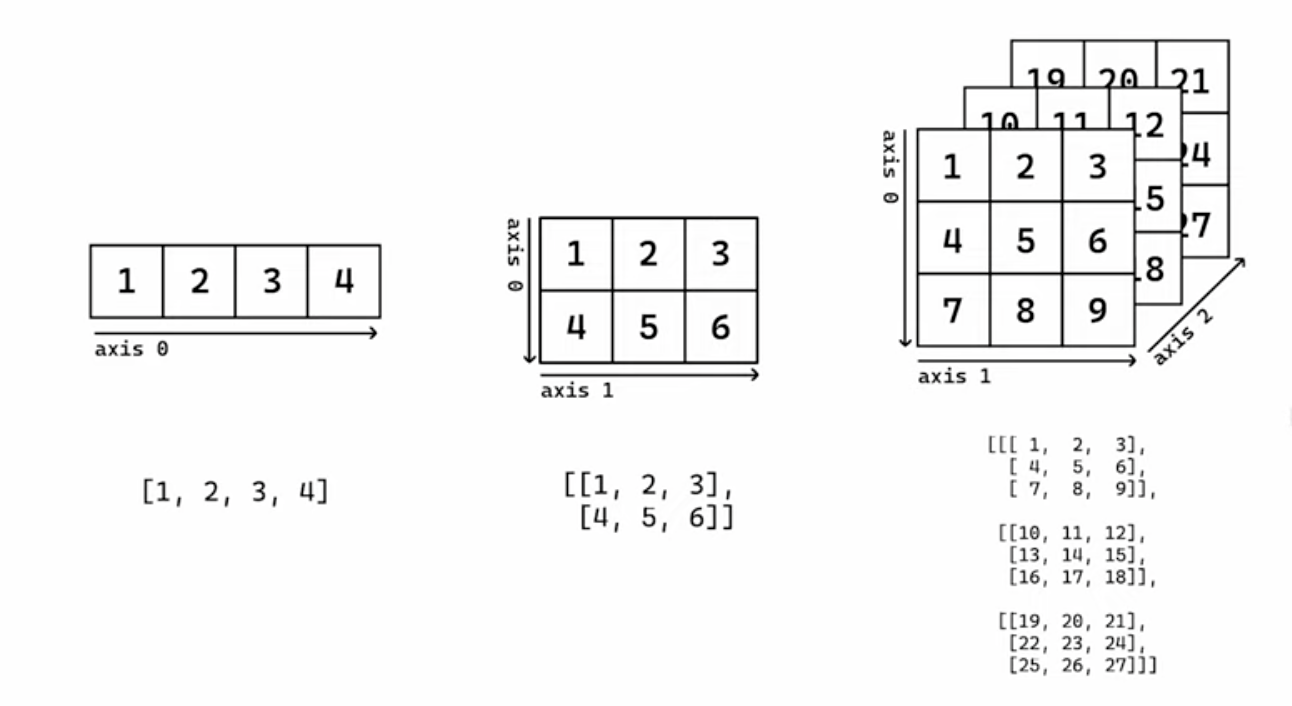
1) 배열 생성하기
# Numpy 패키지 불러오기
import numpy as np
# 배열 생성 메소드
np.array()
np.arange()
np.linspace()
np.zeros()
np.ones()
# 배열 타입 변환
np.astype()
# 배열/데이터 확인
배열명.dtype - 배열의 데이터 타입
배열명.shape - 배열의 형태 '(층, 행, 열)'
배열명.ndim - 배열의 차원(층)
배열명.size - 원소의 총 개수시퀀스 데이터로부터 배열 생성
np.array(seq_data)- 데이터를 직접 넣거나, 데이터가 담긴 변수를 넣어 배열을 생성한다.
# 기본 형태
data1 = [0, 1, 2, 3]
a = np.array(data1)
>>> [0, 1, 2, 3]
# array()에 데이터를 바로 넣어 배열 객체를 생성할 수도 있다.
# 다차원 배열도 생성할 수 있다.
b = np.array([[1, 2, 3], [4, 5, 6]])
>>> [[1 2 3]
[4 5 6]]
# 인자에 정수, 실수가 혼합되어 있으면 모두 실수로 변환한다.
c = np.array([0, 3, 5.2])
>>> [0. 3. 5.2]
# 데이터 타입 확인
a.dtype # dtype('int64')
c.dtype # dtype('float64')
# 배열의 형태 확인
a.shape # (4,)
b.shape # (2, 3)시퀀스 데이터에 정수와 실수가 혼합되어 있으면 모두 실수로 변환하기 때문에, 배열의 속성을 표현하려면 ndarray.속성을 같이 작성해야 한다. (ndarry = NumPy의 배열 객체)
범위 지정해 배열 생성
np.arange([start, ]stop-1[, step])- 1차원 배열 생성np.arange(stop-1).reshape(m, n)- m행*n열 구조의 2차원 배열 생성np.linspace(start, stop[, num])- 정해진 내의 범위에 속하는 데이터의 개수(num) 배열 생성, 실수형np.logspace(start, stop, num, base=n)- n진법의 밑수를 지정한 배열 생성 (base default = 상용로그)
d = np.arange(5)
>>> [0, 1, 2, 3, 4]
e = np.arange(8).reshape(2, 4)
>>> [[0, 1, 2, 3]
[4, 5, 6, 7]]
# rashape() : 배열의 형태 변경
f = np.linspace(1, 10, 5)
>>> [ 1. 3.25 5.5 7.75 10. ]
g = np.logspace(1, 10, 10, base=2) # 2진법의 밑수 지정
>>> [ 2. 4. 8. 16. 32. 64. 128. 256. 512. 1024.]특별히 정해진 형태의 배열 생성
np.zeros(): 모든 원소가 0인 다차원 배열 생성np.ones(): 모든 원소가 1인 다차원 배열 생성np.full(): 모든 원소가 x인 다차원 배열 생성np.eye(): 다차원 행렬에서 주 대각선이 모두 1, 나머지는 0인 단위 행렬 생성
# np.zeros(n), np.zeros((m, n))
h1 = np.zeros(3) # [0. 0. 0.]
h2 = np.zeros((2, 3)) # [[0. 0. 0.], [0. 0. 0.]]
# np.ones(n), np.ones((m, n))
i1 = np.ones(3) # [1. 1. 1.]
i2 = np.ones((2, 3)) # [[1. 1. 1.], [1. 1. 1.]]
# np.full(n, x), np.full((m, n), x)
j1 = np.full(3, 7) # [7, 7, 7]
j2 = np.full((2, 3), 5) # [[5, 5, 5], [5, 5, 5]]
# 단위 행렬
# np.eye(n), np.eye(m, n, k=x)
# (k : 대각선 시작 위치, default=0)
k1 = np.eye(3)
>>> [[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
k2 = np.eye(3, 4, k=-1)
>>> [[0. 0. 0. 0.]
[1. 0. 0. 0.]
[0. 1. 0. 0.]]이미 생성된 배열의 내용을 한 번에 바꿀 수도 있다.
np.zeros_like()np.ones_like()np.full_like()
b = np.array([[1, 2, 3], [4, 5, 6]])
h3 = np.zeros_like(b) # [[0 0 0], [0 0 0]]
i3 = np.ones_like(b) # [[1 1 1], [1 1 1]]
j3 = np.full_list(b, 9) # [[9 9 9], [9 9 9]]배열의 데이터 타입 변환
NumPy 데이터 형식 :
bbool,i기호가 있는 정수,u기호가 없는 정수,f실수,c복소수,M날짜,O파이썬 객체,Sa바이트 문자열,U유니코드
np.array(seq_data, dtype=np.float): 생성 시 배열의 데이터 타입 변경 -dtype=np.타입추가.astype(dtype): 생성 이후 배열의 데이터 타입 변환
# 1. 생성 시 배열 형 변환
## 정수 -> 실수 변환
l1 = np.array([0, 1, 2, 3], dtype=np.flat)
>>> [0., 1., 2., 3.]
# 2. 생성 후 배열 형 변환
## 문자열 -> 실수 변환
l2 = np.array(['1.5', '2']) # ['1.5' '2']
l2.dtype # <U3 : 유니코드, 문자의 수 최대 3
l2.astype(float) # array([1.5, 2. ])
# 그 외 변환
## 실수 형태의 문자열 -> int 변환 시 에러
## 실수 형태의 문자열 -> float 변환 -> int 변환 가능
l3 = j.astype(float)
l3.astype(int) # array([1, 2])
## 정수 0 -> 불 False, 정수 1 -> 불 True난수 배열의 생성
np.random.rand(): 0~1 사이 난수를 요소로 갖는 배열 생성np.random.randint([low, ]high[, size=()]): 지정한 범위에 해당하는 정수로 난수 배열 생성np.random.randn(n): 가우시안 표준 정규 분포에서 난수 n개 배열 생성
m1 = np.random.rand() # 0~1 사이 실수 1개 생성
m2 = np.random.rand(2, 3) # 0~1 사이 실수의 2*3 배열 생성
>>> 0.7625381270859068
>>> [[0.6507446 0.42045933 0.51926107]
[0.93204513 0.15704271 0.21757551]]
n1 = np.random.randint(1, 30)
n2 = np.random.randint(10, size=(2, 3))
>>> 12
>>> [[8 6 6]
[9 7 8]]
o = np.random.randn(3)
>>> [-0.50813153 1.61688176 -0.64076784]np.random.normal(loc, scale, size): 정규분포의 평균, 표준편차, 추출할 표본의 개수를 지정한 배열 생성
p1 = np.random.normal(0, 1, 4)
p2 = np.random.normal(0, 1, (2, 3))
>>> [ 0.28347348 -1.6254198 0.57947124 1.71436408]
>>> [[ 0.76201244 0.54096028 0.31436749]
[ 2.43043434 0.39759195 -0.4196703 ]]
# 여기에 추가로 matplotlib 이용하여 그래프로 표현할 수도 있다.
!pip install matplotlib
import matplotlib.pyplot as plt
plt.hist(p1, bins=10) # bins : 구간
plt.show()
>>> 그래프 생성(응용) 시드값을 통한 난수 생성 제어 :
np.random.seed(1)
q1 = np.random.rand(10)
np.random.seed(1)
q2 = np.random.rand(10)
# q1, q2 모두 같은 값을 갖는다.
# 단, 모두 seed를 각각 설정해주어야 한다.2) 배열의 연산
이러한 벡터 연산은 리스트에서 제어문을 쓰는 것보다 훨씬 빨라서 효율적이다.
기본 연산
배열의 형태(shape)가 같다면 각 원소끼리 사칙연산, 비교연산이 가능하다.
arr1 = np.array([10, 20, 30, 40])
arr2 = np.array([1, 2, 3, 4])
# 덧셈
arr1 + arr2 # array([11, 22, 33, 44])
np.add(arr1, arr2)
# 뺄셈
arr1 - arr2 # array([9, 18, 27, 36])
np.subtract(arr1, arr2)
# 곱하기
arr1 * 2 # array([20, 40, 60, 80])
arr1 * arr2 # array([10, 40, 90, 160])
np.multiply(arr1, arr2)
# 나눗셈, 몫, 나머지
arr1 / arr2 # array([10., 10., 10., 10.])
np.divide(arr1, arr2)
arr1 // 2 # array([ 5 10 15 20])
arr1 % 2 # array([0 0 0 0])
# 제곱
arr1 ** 2 # array([100, 400, 600, 1600])
np.square(arr1)
# 제곱근
arr3 = np.array([1, 9, 16])
np.sqrt(arr3) # array([1., 3., 4.])
# 비교 연산
arr1 > arr2 # array([ True, True, True, True])
arr1 > 20 # array([ False, False, True, True])
np.array_equal(arr1, arr2) # False
# 삼각함수
np.sin(arr1)
np.cos(arr1)
np.tan(arr1)
# PI
np.pi()통계를 위한 연산
- 메소드를 이용해 배열의 합, 평균, 표준 편차, 분산, 최솟값/최댓값, 중앙값, 누적합/누적곱 등을 구할 수 있다.
- 메소드를 이용해 절댓값, 올림, 내림, 반올림, 버림도 구할 수 있다.
arr = np.arange(1, 5) >>> [1, 2, 3, 4]
arr2 = np.array([[1, 2, 3],
[0, 1, 4]])
np.sum(arr)
arr.sum() # 합 : 10
arr2.sum(axis=0) # [1, 3, 7] - (1,0), (2,1), (3,4)
arr2.sum(axis=1) # [6, 5] - (1, 2, 3), (0, 1, 4)
np.mean(arr)
arr.mean() # 평균 : 2.5
arr2.mean(axis=0) # [0.5, 1.5, 3.5]
arr2.mean(axis=1) # [2., 2.5]
np.std(arr)
arr.std() # 표준편차 : 1.118033988749895
arr2.std(axis=0) # [0.5 0.5 0.5]
arr2.std(axis=1) # [0.81649658 1.69967317]
arr.var() # 분산 : 1.25
np.min(arr)
arr.min() # 최솟값 : 0
arr2.min(axis=0) # [0, 1, 3]
arr2.min(axis=1) # [1, 0]
np.max(arr)
arr.max() # 최댓값 : 4
arr2.max(axis=0) # [1, 2, 4] max(3,4)
arr2.max(axis=1) # [3, 4]
np.median(arr) # 중앙값 : 2.5
np.median(arr2) # 1.5
np.median(arr2, axis=0) # [0.5 1.5 3.5]
np.median(arr2, axis=1) # [2. 1.]
np.cumsum(arr)
arr.cumsum() # 누적합 : [1, 3, 6, 10]
np.cumsum(arr2) # [ 1 3 6 6 7 11]
arr2.cumsum(axis=0) # [[1 2 3] [1 3 7]]
arr2.cumsum(axis=1) # [[1 3 6] [0 1 5]]
np.cumprod(arr)
arr.cumprod() # 누적곱 : [1, 2, 6, 24]
np.cumprod(arr2) # [1 2 6 0 0 0]
arr2.cumprod(axis=0) # [[ 1 2 3] [ 0 2 12]]
arr2.cumprod(axis=1) # [[1 2 6] [0 0 0]]arr = np.array([1, -2, 1.6, -2.3, -4.8])
np.abs(arr) # 절댓값 : [1. , 2. , 1.6, 2.3, 4.8]
np.ceil(arr) # 올림 : [ 1., -2., 2., -2., -4.]
np.floor(arr) # 내림 : [ 1., -2., 1., -3., -5.]
np.round(arr) # 반올림 : [ 1., -2., 2., -2., -5.]
np.trunc(arr) # 버림 : [ 1., -2., 1., -2., -4.]브로드캐스팅 - 서로 다른 형태의 배열 연산
# 서로에게 맞춰 확장됨
arr1 = np.array([1, 1, 1])
arr2 = np.array([[0], [1], [2]])
arr1+arr2
>>> [[1 1 1]
[2 2 2]
[3 3 3]]3) 배열의 인덱싱/슬라이싱
✔️ 인덱싱
- Fancy 인덱싱 : 특정 인덱싱을 여러 개 선택해서 탐색하는 방법
- Boolean 인덱싱 : T/F을 이용하여 배열의 인덱싱을 탐색하는 방법
값 선택 : 특정 위치 or 여러 개의 원소를 선택할 수 있다.
값 변경 : 인덱싱 개수에 맞게 새로운 값을 지정하거나 단 하나의 값을 지정해 변경 가능하다.
- 1차원 배열
- (Basic)
배열명[i]- 1차원 배열에서 특정 위치 원소 선택 - (Fancy)
배열명[[i, ..]]- 1차원 배열에서 여러 개의 원소 선택 - (Boolean)
배열명[[True/False, ..]]- 1차원 배열에서 T에 해당하는 인덱싱 선택 - (Condition)
배열명[조건]- 1차원 배열에서 조건에 맞는 배열의 원소만 선택
arr1 = np.array([0, 1, 2, 3])
# 1차원 배열 인덱싱
arr1[2] # 2
arr1[[1, 3]] # array([1, 3])
arr1[[True, True, True, False]] # array([0, 1, 2])
arr1[arr1 < 3] # array([0, 1, 2])
# 1차원 배열 값 변환
arr1[2] = 5 # [0, 1, 5, 3]
arr1[[1, 3]] = 7 # [0, 7, 5, 7]
arr1[[1, 3]] = 8, 9 # [0, 8, 5, 9]- 2차원 배열
- (Basic)
배열명[행_위치, 열_위치]or배열명[i][j]- 2차원 배열에서 특정 위치 원소 선택 - (Fancy)
배열명[[행_위치, ..], [열_위치, ..]]- 2차원 배열에서 여러 개의 원소 선택 (행과 열에 각각 조건 부여 가능) - (Boolean)
배열명[[T/F], [T/F]] - (Condition)
배열명[조건]- 1차원 배열로 반환한다.
arr2 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# 2차원 배열 인덱싱
arr2[1] # array([4, 5, 6])
arr2[:, 1] # array([2, 5, 8])
arr2[1, 2] # 6
arr2[[0, 2], [1, 1]] # array([2, 8])
arr2[[True, False, False], True] # array([[1, 2, 3]])
arr2[arr2 > 5] # array([6, 7, 8, 9])
# 2차원 배열 값 변환
arr2[1, 2] = 0 # [[1, 2, 3], [4, 0, 6], [7, 8, 9]]
arr2[1] = np.array([1, 2, 3]) # [[1, 2, 3], [1, 2, 3], [7, 8, 9]]
arr2[1] = [7, 8, 9] # [[1, 2, 3], [7, 8, 9], [7, 8, 9]]✔️ 슬라이싱
1차원 배열[start:end-1:step]2차원 배열[행start:행end-1, 열start:열end-1]
값 변경 : 인덱싱과 마찬가지로, 슬라이싱 개수에 맞게 새로운 값을 지정하거나 단 하나의 값을 지정해 변경 가능하다.
arr2 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
arr2[1:3, 1:3] # array([[5, 6], [8, 9]])4) 배열의 정렬
np.sort(arr): 오름차순 정렬, 원본 배열에 영향 xarr.sort(): 오름차순 정렬, 원본 배열에 영향 o
arr2 = np.array([[6, 0, 8, 5], [5, 0, 9, 4]])
np.sort(arr2) # [[0 5 6 8] [0 4 5 9]]
np.sort(arr2, axis=1) # [[0 5 6 8] [0 4 5 9]]
np.sort(arr2, axis=0) # [[5 0 8 4] [6 0 9 5]]
np.sort(arr2, axis=None) # [0 0 4 5 5 6 8 9]
np.argsort(arr2) # [[1 3 0 2] [1 3 0 2]]
np.argsort(arr2, axis=1) # [[1 3 0 2] [1 3 0 2]]
np.argsort(arr2, axis=0) # [[1 0 0 1] [0 1 1 0]]행렬 연산
선형 대수를 위한 행렬(2차원 배열) 연산도 가능하다. 행렬 A와 B에 대한 행렬 곱, 전치 행렬, 역행렬, 행렬식을 구할 수 있다.
- 행렬 곱 (matrix product) :
A.dot(B)ornp.dot(A,B) - 전치 행렬 (transpose matrix) :
A.transpose()ornp.transpose(A) - 역행렬 (inverse matrix) :
np.linalg.inv(A) - 행렬식 (determinant) :
np.linalg.det(A)
a = np.array([2, 3, 4])
b = np.array([1, 2, 3])
np.dot(a, b) = 20 # (2*1) + (3*2) + (4*3)
A = np.array([0, 1, 2, 3]).reshape(2, 2)
>>> [[0 1]
[2 3]]
B = np.array([9, 5, 4, 6]).reshape(2, 2)
>>> [[9, 5]
[4, 6]]
# 행렬 곱 (matrix product) - A.dot(B) or np.dot(A,B)
# 두 행렬의 형태가 같아야 한다.
'''
[[a, b] [[e, f] [[ae + bg, af + bh]
[c, d]] [g, h]] [ce + dg, cf + dh]]
'''
array([[ 4, 6],
[30, 28]])
# 전치 행렬 (transpose matrix) - A.transpose() or np.transpose(A)
array([[0, 2],
[1, 3]])
# 역행렬 (inverse matrix) - np.linalg.inv(A)
array([[-1.5, 0.5],
[ 1. , 0. ]])
# 행렬식 (determinant) - np.linalg.det(A)
-2.0배열의 정렬
.reshape(): 배열의 형태 변경, 원본 데이터 변경 x.resize(): 배열의 형태 변경, 원본 데이터 변경 o.ravel(): 1차원 배열로 변경
arr = np.array([0, 1, 2, 3, 4, 5])
arr.reshape(2, 3) # [[0 1 2], [3 4 5]]
arr.reshape(2, -1) # [[0 1 2], [3 4 5]] # -1 : 지정되지 않은 하나의 차원 자동 계산
arr.resize(2, 3) # [[0 1 2], [3 4 5]]
arr.ravel() # [0, 1, 2, 3, 4, 5]np.expand_dims(arr, axis): 입력한 값을 기준으로 차원 추가np.squeeze(arr, axis): 한 차원씩 축소
arr1 = np.array([1, 2, 3])
np.expand_dims(arr2, axis=0) # [[1 2 3]]
np.expand_dims(arr2, axis=1) # [[1] [2] [3]]
arr2 = np.array([[1, 2]]) # [[1, 2]] (1, 2) 2
np.squeeze(arr2, axis=0) # [1 2] (2,) 1
arr3 = np.array([[[1, 2, 3]]]) # [[[1, 2, 3]]] (1, 1, 3) 3
np.squeeze(arr2, axis=1) # [[1, 2, 3]] (1, 3) 25) 배열 추가, 삭제, 병합, 분할
np.insert(배열, 인덱스, 원소값): 배열에 원소 추가
arr1 = np.arange(1, 6) # [1, 2, 3, 4, 5]
np.insert(arr1, 2, 30) # [1, 2, 30, 3, 4, 5]
arr2 = np.arange(1, 7).reshpe(2, 3) # [[1, 2, 3], [4, 5, 6]]
np.insert(arr2, 1, 30, axis=0) # [[1, 2, 3], [30, 30, 30], [4, 5, 6]]
np.insert(arr2, 1, 30, axis=1) # [[1, 30, 2, 3], [4, 30, 5, 6]]
np.insert(arr2, 1, 30) # [1, 30, 2, 3, 4, 5, 6]np.delete(배열, 인덱스, axis): 배열에 원소 삭제
arr1 = np.arange(1, 6) # [1, 2, 3, 4, 5]
np.delete(arr1, 2) # [1, 2, 4, 5]
arr2 = np.arange(1, 7).reshpe(2, 3) # [[1, 2, 3], [4, 5, 6]]
np.delete(arr2, 1, axis=0) # [[1, 2, 3]]
np.delete(arr2, 1, axis=1) # [[1, 3], [4, 6]]
np.delete(arr2, 1) # [1, 3, 4, 5, 6]np.append(배열1, 배열2, axis): 배열 간의 병합np.vstack(배열1, 배열2): x축을 기준으로 병함np.hstack(배열1, 배열2): y축을 기준으로 병합np.concatenate([배열1, 배열2], axis)
arr1 = np.arange(1, 7).reshape(2, 3) # [[1, 2, 3], [4, 5, 6]]
arr2 = np.arange(7, 13).reshape(2, 3) # [[7, 8, 9], [10, 11, 12]]
np.append(arr1, arr2, axis=0) # 1차원 배열로 병합
>>> [1 2 3 4 5 6 7 8 9 10 11 12]
np.append(arr1, arr2, axis=0) # x축을 기준으로 병합
np.vstack(arr1, arr2)
np.concatenate([arr1, arr2], axis=0)
>>> [[1 2 3], [4 5 6], [7 8 9], [10 11 12]]
np.append(arr1, arr2, axis=1) # y축을 기준으로 병합
np.hstack(arr1, arr2)
np.concatenate([arr1, arr2], axis=1)
>>> [[1 2 3 7 8 9], [4 5 6 10 11 12]]np.vsplit(배열, 분할 수): axis=0, x축을 기준으로 배열 분할 (분할 안 되는 숫자는 에러)np.hsplit(배열, 분할 수): axis=1, y축을 기준으로 배열 분할 (분할 안 되는 숫자는 에러)
arr3 = np.arange(1, 13).reshape(3, 4)
>>> [[1 2 3 4]
[5 6 7 8]
[9 10 11 12]]
np.vsplit(arr3, 3)
>>> array([[1 2 3 4]]), array([[5 6 7 8]]), array([[9 10 11 12]])
np.hsplit(arr3, 2)
>>> array([[1 2], [5 6], [9 10]]), array([[3 4], [7 8], [11 12]])🖐️ 자세한 내용은 NumPy 홈페이지 참고!