[NLP] RNN

RNN

기존의 신경망 구조를 그림으로 나타내면 아래와 같다.

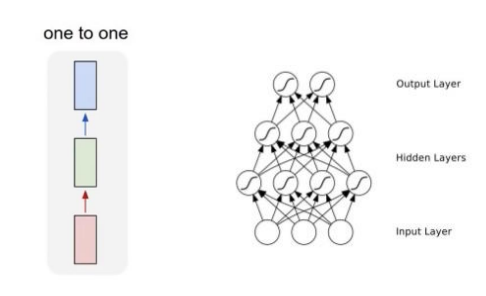
Vanilla neural network은 순서의 개념 없이 입력을 넣으면 출력이 나오게 된다. 하지만, 텍스트의 경우 문장 내 단어들은 앞뒤 위치에 따라 서로 영향을 주고 받게 된다. 따라서, 이러한 순서의 개념을 반영하여 순차적으로 입력을 넣고, 출력이 순차적으로 반환되는 함수가 필요했다. 이를 RNN(Recurrent Neural Network)로 해결 할 수 있었다.

Vanilla neural network가 정해진 입력 x를 받아 y를 출력해주는 형태였다면, RNN은 i번째 값 $x_i$와 직전의 hidden state인 $h_{t-1}$을 바탕으로 현재의 hidden state $h_t$를 결정하는 과정을 매 time-step마다 진행하게 된다.
이를 수식으로 표현하면 다음과 같다.

Feed-forward

기본적인 RNN을 활용한 feed-forward의 흐름을 살펴보면 다음과 같다.

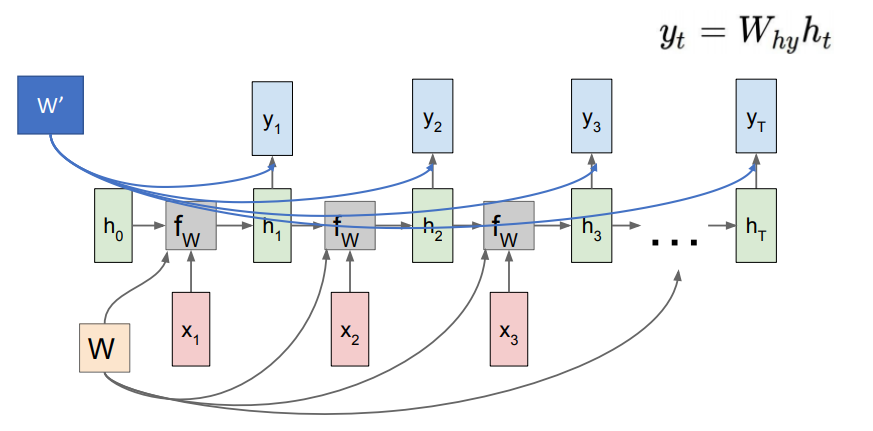
여기서 현재 time-step을 i라고 했을 때, $h_i$를 구하는 과정은 앞서 말한것처럼 $x_i$와 $h_{t-1}$을 input으로 받아 계산된다. 이를 수식으로 나타내면,

여기서 $W_{ih}$와 $W_{hh}$는 서로 다른 가중치이다.

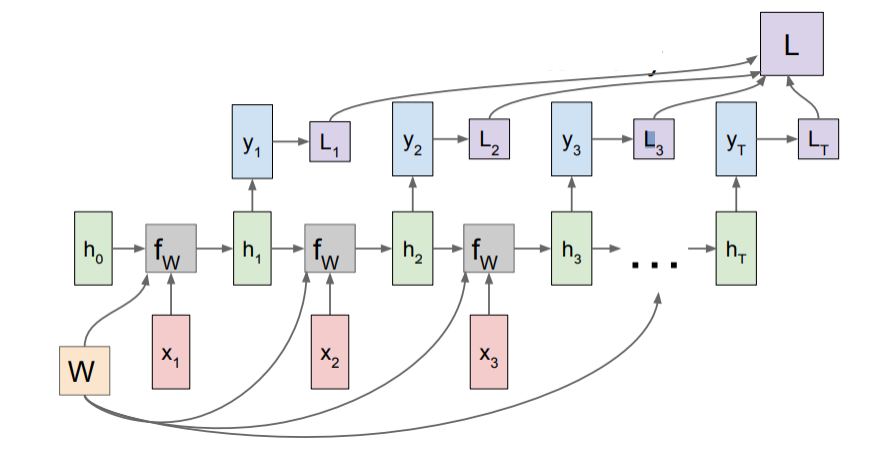
이처럼 매 time-step별 $y_t$를 계산하여 손실 L을 구한 후 time-step의 수만큼 평균을 내어 최종적인 loss value를 계산하게 된다.

BPTT

이렇게 구해진 loss value L을 바탕으로 back propagation을 수행하면 각 time-step별로 마지막 time-step과 가까운 parameter($\theta_t$)의 기울기가 구해지고, 이전 time-step의 parameter($\theta_{t-1}$)에 더해지게 된다. 즉, time-step이 0(초기)에 가까워질수록 parameter($\theta_0$)의 기울기는 점점 커지게 된다. 이를 BPTT(Back-propagation through time)이라고 불린다. 이러한 속성으로 인해, RNN은 time-step수만큼 layer가 존재하는 것과 유사하게 된다.

앞서 작성된 수식을 보면, activation function으로 $tanh$를 사용한 것을 볼 수 있으며, $tanh$ 함수의 특징은 $x$값이 커질수록 $tahn(x)$값이 -1과 1에 근접함과 동시에 기울기가 0에 가까워지게 된다. 이와 같은 성질로 인해, time-step이 많아질수록 gradient vanishing 현상이 나타나게 된다.

NLP에 RNN 적용 사례

RNN의 입출력은 다음과 같이 분류할 수 있다.

input	output	remark
many	one	many to one
many	many	many to many
one	many	one to many

하나의 출력을 사용할 경우
마지막 time-step의 output을 결과로 사용하며, 적용되는 가장 흔한 예제는 sentimental analysis (감성분석)이다. token(단어)의 개수만큼 입력이 들어가 마지막 time-step의 결과값을 받아 softmax함수를 거쳐 해당 class를 예측하게 된다.

모든 출력을 사용할 경우
모든 time-step의 출력값을 사용하며 language modeling (언어모델)이나 machine translation(기계번역)등 외 다양한 분야에 사용된다. time-step별로 one-hot vector을 입력으로 받아 embedding layer을 거쳐 dense vector을 만들고 RNN을 거쳐 time-step별로 output이 구해지면, time-step별로 softmax 함수를 거쳐 loss value를 계산하게 된다. 대부분의 경우 RNN은 여러 층과 양방향으로 구현할 수 있지만, 입출력이 서로 같은 데이터를 공유할 경우에는 양방향 RNN을 사용할 수 없다. 즉, 이전 time-step에서 사용된 출력값이 현재의 입력으로 쓰이는 모델 구조(autoregressive model)는 bidirectional RNN을 사용할 수 없는 것이다.