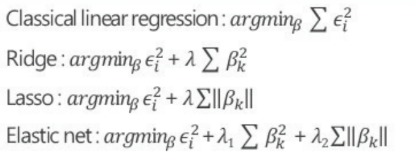DataScience 3

정선용·2024년 2월 4일

DataScience

목록 보기

3/7

선형회귀분석

통계파트(기울기, 절편 구하는 법)

회귀분석

개념
연속형 변수들 사이의 모형을 구한 뒤 적합도를 측정해내는 분석 방법.

목적
* 설명 : 종속변수에 대한 설명변수(독립변수) 의 영향을 측정, 설명.

	* 예측: 설명변수(독립변수) 정보가 있을 때 이에 따른 종속변수를 예측.
  ![](https://velog.velcdn.com/images/jeongsunyong/post/44d57321-fab3-4ca2-b8d8-4dfe327a0a95/image.png)

종류
예측함수의 형태에 따라 선형회귀 / 비선형회귀
독립변수의 개수에 따라 단순회귀 / 다중회귀
* 종속변수의 개수에 따라 단변량회귀 / 다변량회귀

단순 선형 회귀분석 - 최소제곱법

수학적 표현

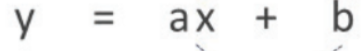
y : 종속변수, x : 독립변수, a : 기울기, b : 절편
통계적 표현

β0 : 절편 , β1 : 기울
오차
오차(E) = 측정값(M) - 참값(T)
측정값(관측값)과 참값(실제값)의 차, 오차가 작을수록 좋은 모델.

최소제곱법(Ordinary Least Squares, OLS)
* 단순회귀모형 Yi = α + βxi + εi에서 오차의 제곱합이 최소가 되도록 α, β를 추정하는 방법.

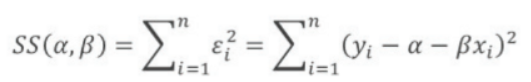
	* 최선의 직선을 찾는다는 것은 구해진 선과 데이터 사이의 오차를 최소화하는 것.
	* 오차 구할 시 값에 절대값 / 제곱을 해서 구하는데, 수학적으로 절대값을 씌우면 미분을 하지 못하므로 제곱하는 방법 보통 이용.

단순 선형 회귀분석 - 최소제곱 추정량 hat{α}, hat{β}

최소제곱 추정량

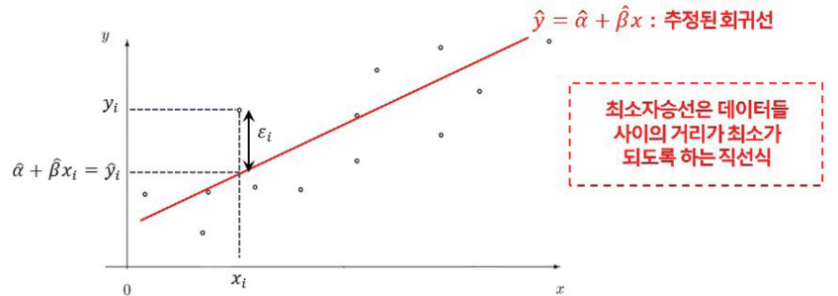
최소제곱법은 오차 제곱합이 최소가 되도록 α , β를 추정하는 방법이고, 이 때의 알파 베타가 최소제곱 추정량이다.
SS가 최소가 되는 회귀계수 hat{α}, hat{β}를 구하기 위해서는 SS를 α , β로 편미분한 값을 0으로 둠.

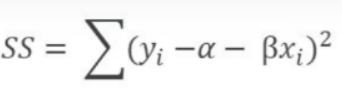
단순 선형 회귀분석 - 회귀계수 추정량 hat{α}, hat{β} 도출방법

★정규방정식 (Normal Equation) : 오차 제곱합 SSE가 최소가 되게 α , β를 추정하고, 이를 α , β에 대해 각각 미분 (cost function 미분)후 두 개의 방정식을 정리한 것.
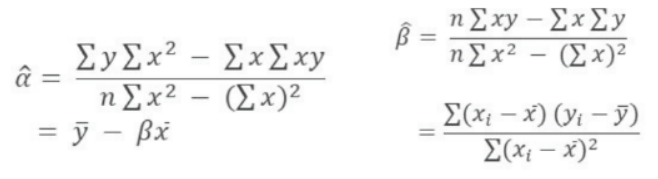
- α 에 대해 정리한 식 : 절편을 구하는 공식
- β에 대해 정리한 식 : 기울기를 구하는 공식
회귀식 구하는 방법
1. x,y 좌표의 평균 구하기
2. 기울기 구하기
* 3. 절편 구하기

최소제곱법 예제

최소제곱법 예제
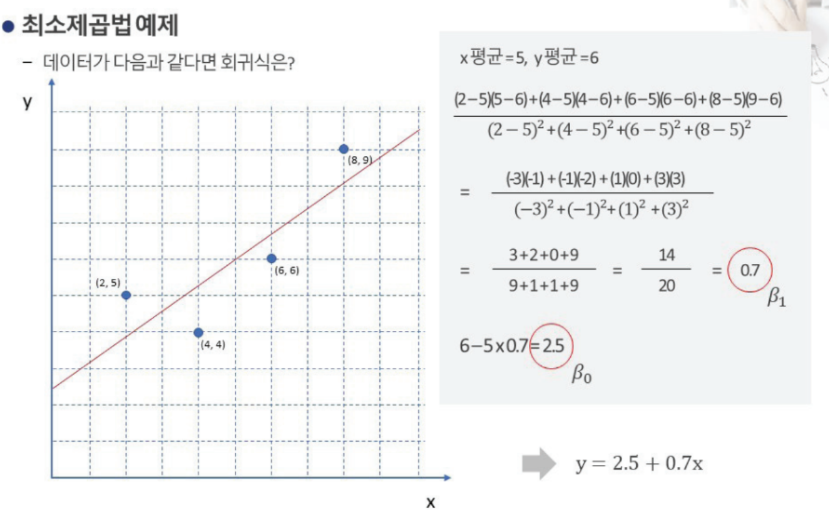
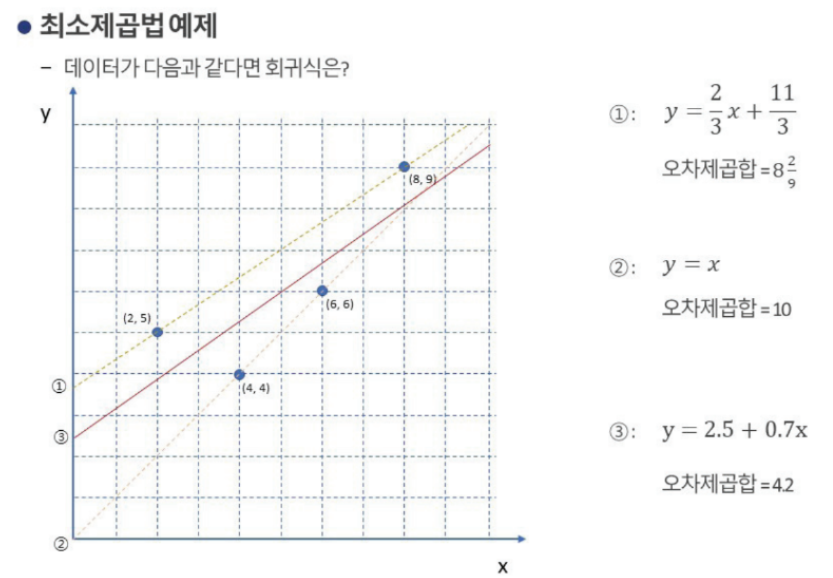
- x바, y바 : (2+4+6+8)/4, (5+4+6+9)/4 = 5,6
- 기울기 : 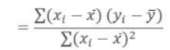= ((2-5)(5-6) + (4-5)(4-6) + (6-5)(6-6) + (8-5)(9-6)) / (9+1+1+9)
  = (3+2+0+9)/20 = 14/20 = 0.7
- y절편 :
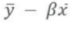
  = 6 - 5 * 0.7 = 6 - 3.5 = 2.5
  
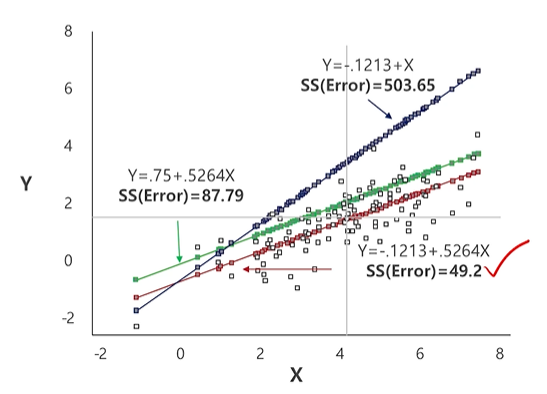
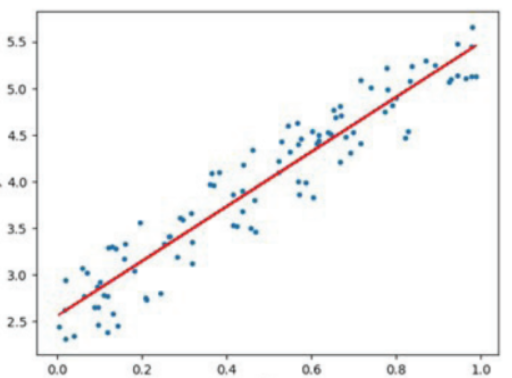
  위 그림에서 가장 적합한 선형회귀식은 y = -0.1213+0.5264x

통계파트(주요 가정)

회귀분석의 가설검정

선형 회귀분석의 가설
- 귀무가설(H0) : X변수들은 Y변수와 선형관계가 없음(기울기 β1 = 0)
- 대립가설(H1) : X변수들은 Y변수와 선형관계까 있음(기울기 β1 != 0)
검정통계량
- F검정 : 회귀 모형의 통계적 유의성을 검정
- t검정 : 개별 독립변수가 종속변수에 유의한 영향을 미치는지 검정
- 단순회귀분석의 경우 : F검정과 t검정 결과는 동일
- 다중회귀분석의 경우 : F검정의 결과 회귀 모형이 통계적으로 유의하다고 판단되면 개별 독립변수에 대한 t검정 유의성을 확인.

회귀분석의 주요 가정

4가지 가정 중요. 선형성은 전체 데이터 분포와 관련, 정규성,등분산성,독립성은 오차에서 사용되는 가정.

1. 선형성
- 종속변수 Y는 독립변수 X에 대하여 선형적 관계를 가짐
- 선형성 가정에 대한 검토
  - (1) 산점도로 선형성 확인
  - (2) 상관계수 확인
  - (3) 회귀계수 β에 대한 검정

독립성
* 오차는 Random Variable, 독립적이며 동일하게 분포하는 확률분포이다.

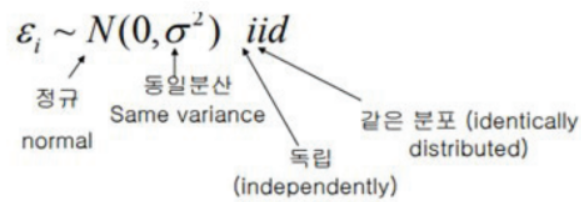
* 독립성 가정에 대한 검토
  * (1) 예측값 대 잔차 산점도
  * (2) 더빈왓슨 테스트

1. 정규성
  오차는 모두 평균이 0이고 분산이 σ^2인 정규분포
  정규성 가정에 대한 검토
  (1) 산점도 / Histogram / Q-QPlot
  (2) 잔차에 대한 왜도 및 첨도 검토
  * 정규성 가정이 성립하지 않으면 분산분석을 할 수 없다.
4.등분산성
분산 σ^2은 모든 X에 대하여 일정한 상수
등분산성 가정에 대한 검토
(1) 예측값 대 잔차 산점도
(2) 잔차의 등분산성에 대한 검정(WhiteTest, Breusch-Pagantest )
* 등분산성이 성립하지 않으면 F검정, t검정 사용할 수 없다.

회귀분석의 가정을 만족하지 못할 때

1. 선형성 이슈 : 독립변수와 종속변수가 선형관계가 아닌경우
  산점도 그래프와 회귀선으로 확인한다.
  대응 방법
  데이터 변환
  다향 회귀(Polynomial Regression) : 독립변수가 다항으로 구성된 회귀 모형(지수승)
  * 일반화 가법 모델(Generalized Additive Model) : 다른 선형 함수 결합으로 표현
1. 정규성 이슈 : 오차항의 확률분포가 정규분포가 아닌 경우
- Q-Q Plot으로 확인한다.
- 대응 방법
  - 데이터 변환
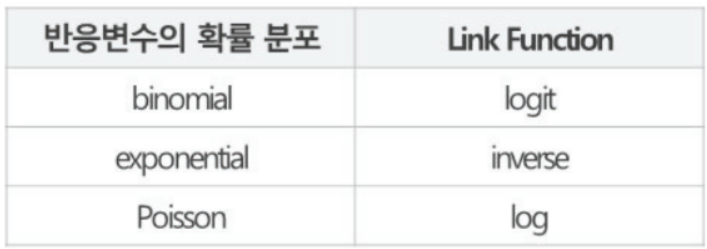
  - 일반화 선형 모형(Generalized Linear Model) : 종속 변수에 변환 함수를 적용
    변환함수를 Link Function이라 한다. 반응 변수의 확률분포에 따라 사용하는 함수가 달라짐
1. 등분산성 이슈 : 오차항의 확률분포가 등분산이 아닌 경우
- 잔차 그래프로 확인한다.
- 대응 방법
  - 데이터 변환 : 이상치 제거(데이터 변환/가중선형회귀방법 사용 전 이상치 먼저 제거해본다.)
  - 가중 선형 회귀(Weighted Linear Regression)
    * 잔차에 가중치 적용한 제곱값을 최소화. 가중치는 해당 관측치 분산의 역수이며, 분산이 작은 관측치는 신뢰하고 분산이 큰 관측치는 신뢰하지 않는다.
4.독립성 이슈 : 오차항이 독립이 아닌 경우 / 자기상관성이 있는 경우
- 더빈 왓슨(Durbin-Watson) 통계량으로 확인한다.
- 대응 방법
  - 자기 회귀 모델(AutoRegressive Model)
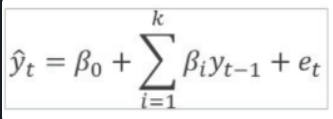
    - 시계열 같이 순서가 정해져있는 데이터 주기성/계절성 등 패턴이 나타나는, 자기 상관성이 있는 경우의 모델
    - 시간에 따라 평균이 변하는 경우 : Auto-Regressive Moving Average(ARMA) Model
    - 시간에 따라 분산이 변하는 경우 : Auto-Regressive Conditionally/Heteroscedastic(ARCH) Model
    - ARMA 모델 일반화 : Auto-Regressive Integrated Moving Average Model

통계파트(변수처리, 성능평가)

다른 이슈가 있는 데이터 일 때

1. 이상치(Outliers) 이슈 : 잔차가 대부분의 다른 데이터와 확연하게 차이가 나는 큰 값
- 히스토그램, 막대그래프 등으로 확인한다.
- 대응 방법
  - 데이터 변환
  - Robust Regression : 잔차의 '제곱' 대신 '절대값'의 합이 최소가 되도록 계수 추정 방식.
  - Quantille Regression : 평균이 아닌 특정 분위값을 추정하는 방식. 이분산 데이터에도 회귀분석 적용 가능.
1. 다중공산성 이슈 : 독립변수 간 강한 상관관계가 있는 경우
- 상관분석(VIF, Variance Inflation Factor) 로 확인한다.
  - VIF가 클수록 다중공산성 존재한다고 판단
- 대응 방법
  - Feature Engineering (특성공학)
  - Regularization (정규화)
    - Ridge Regression / LASSO / Elastic net
    - PCR (Principal Component Regression) : 차원 축소/변형, 주성분분석
    - PLS (Partial Least Square Regression) : 종속변수와 독립변수의 관계를 가장 잘 설명하는 축을 찾아 전사하는 방식. 종속,독립변수 모두 변형

선형회귀모델 평가

잔차 분석
잔차 시각화를 통한 회귀분석 가정 검토.

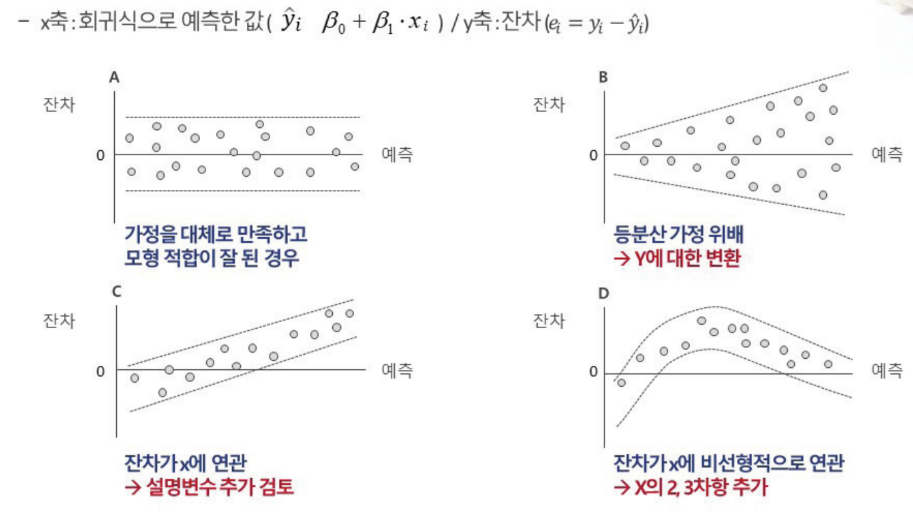
c의 경우, 기울기가 존재하면 안되는데 존재
A: 등분산,독립, B:등분산 X, C : 독립X, D : 선형성만족X
1. 유의성 검정
- 회귀모델 : F 검정통계량에 대한 확률(p-value) : 회귀식이 종속변수 y의 변량을 설명하는가?
- 회귀변수 : 각 독립변수의 t 검정통계량에 대한 확률(p-value) : 해당 독립변수가 종속변수 y의 변량을 설명하는가?
1. 적합성 검정
- ★R^2 (결정계수, coefficience of determination)
  - 변수간 영향을 주는 정도 또는 인과관계의 정도를 정량화해서 나타낸 수치
  - 추정한 선형 모형이 주어진 자료에 대해 얼마나 적합한가를 나타냄.
  - SSR은 회귀식과 Y의 평균값과의 차이를 말하며, SSR이 존재한다는 것은 회귀식이 전재한다는 것과 같은 의미. 총변동으로 나누게 되면 결정계수가 된다.
  - 0<= R^2 <= 1 , 1에 가까울수록 인과관계 높다.
  - Adjusted R^2 : 독립변수를 추가하면 R^2 값은 상승하므로 Adjusted R^2 사용.
- 결정계수 활용 시 고려 사항
  - 결정계수는 적합성에 대한 완전한 지표가 아님. 선형 적합도를 측정하는 한가지 방법임.
  - 예측 오차에 대한 지표가 아님.
  - 한 변수가 다른 변수에대해 얼마나 설명하는가를 측정하는 것은 아님
  - 종속변수에 대해 원시자료를 사용한 경우와 변수 변환 간 결정계수 비교는 적절치 않음 -> 회귀모델 적절한데 낮은 결정계수 갖는 경우, 결정계수 값 높은데 회귀모델이 적절하지 않은 경우 등도 존재하므로 , 다른 평가 지표와 함께 활용하는 것이 좋다.
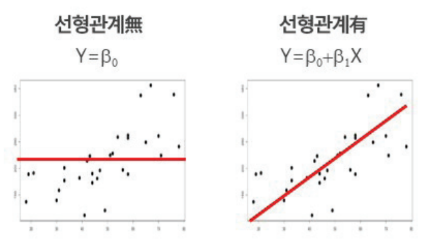
- 회귀모델 : 오차 지표(MSE, RMSE, MAE, MAPE)
  - 오차 : 실제 y값과 회귀 모형에 의한 ybar 간 차이
  - 학습오차:모델 적합에 사용한 데이터로 측정한 오차
  - 예측오차:모델 적합에 사용하지 않은 데이터로 측정한 오차

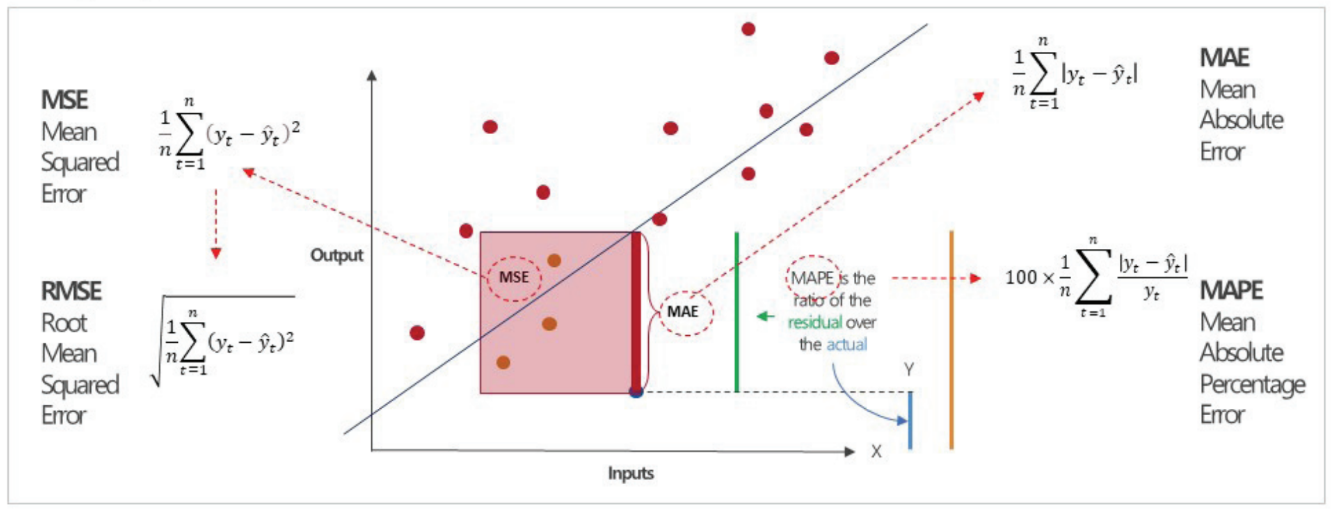
회귀 모델에서 명목형 변수처리

잔차 분석
- 범주형 데이터를 수치형 데이터로 변환( 숫자 형태 code로 변경, 범주형 자료 0과 1로 표현- one hot encoding)
- 해당 범주형 변수의 기준값을 정함.
- 그 값을 제외한 나머지 범주형 값을 새로운 열이름으로 하여 열 추가
- 모든 셀 값은 0, 행의 원래 값과 열이름이 같은 셀만 1을 가짐.

일부 개념 review 지수분포 - 무기억성, 점추정조건, 회귀분석 - 영향점

지수분포

무기억성
사건 E가 S만큼의 시간 동안 발생하지 않았을 때 이후 만큼 기다린 후 발생될 확률은 앞의 기다린 시간 S를 무시하고 T부터 기다린 후 발생될 확률과 같다. : 앞에 기다렸던 시간 S는 무시한다.
- (P(X>S+T | X>S)=P(X>T)
점추정 조건
- 추정량의 종류
  - 불편추정량 : 표본에서 구한 기대값이 모수와 같아지는 추정량
    - 모수 u의 추정량 T(X)가 E[ T(X) ]=u를 만족하면 이때 추정량 T(X)를 모수 u의 불편추정량이라고 한다.
  - 일치추정량 : 샘플의 개수가 많아질수록 추정량이 모수와 같아짐
    - 임의 표본 (X1, X2, ..,, Xn)에서 나온 표본평균은 항상 E(X)로 확률1로 수렴. (표본평균은 항상 모집단의 평균으로 수렴한다)
  - 유효추정량 : 모수의 불편 추정량 가운데에서 분산이 작은 불편 추정량 (ex 2개 정규분포 평균이 같을 때 분산이 작은 정규분포가 더 유효하게 추정할 수 있음)
  - 충분통계량 : 표본이 가지고 있는 모수에 대한 모든 정보와 동일한 정보량을 가지는 통계량
    
    : 통계량 조건부 분포가 theta에 의존하지 않는다는 것은 S(X)가 이미 theta에 대한 모든 정보를 설명하고 있기 때문에 S(X)가 주어지고 나머지 정보는 theta를 설명하는 데 아무 쓸모가 없다는 뜻.
- 일반적 추정 방법
  - 최우추정량(최대우도추정법 : MLE)
    : 현상이 발생할 가능성을 찾아 이를 최대화 할 수 있는 상태를 최적의 상태로 보는 법. 점추정의 한 방법으로 적률법과 함께 사용하며, 용어정도만 알아두면 된다.