데이터 전처리
데이터 크리닝
데이터 전처리
- 개념
: 데이터 품질에 관계 없이 분석 작업 전에 데이터를 분석하기 좋은 형태로 만드는 과정 - 데이터 전처리가 필요한 경우
- 구조적 형태가 분석 목적에 적합하지 않은 경우
- 사용하는 툴, 기법에서 요구하는 데이터 형태
- 데이터가 너무 많은 경우
- 데이터 품질이 낮은 경우
- 불완전(Incomplete) : 데이터의 필드가 비어 있는 경우 (ex 결측치)
- 잡음(Noise) : 데이터에 오류가 포함된 경우 (ex 이상치)
- 모순(Inconsistency) : 데이터 간 정합성, 일관성이 결여된 경우 (ex 수치 및 범주형 데이터가 혼합된 경우)
- 주요 기법
- 정제(Clearning)
- 통합(Integration)
- 축소(Reduction)
- 변환(Transformation)
데이터 정제
-
결측값 (Missing Value)
: 존재하지 않고 비어있는 상태, DB에서 NULL값인 경우.
후속 분석 결과에 영향이 최소화되도록 데이터를 채울 필요가 있다.- 처리 방법
- 수작업으로 채워넣기
- 특정값 사용
- 평균값 사용 (전체평균 혹은 기준속성 평균)
- 해당 데이터 행을 모두 제거
- 처리 방법
-
이상값 (Outlier)
: 대표적인 잡음 요소. 이상값으로 판단되는 값에 의해 경향성 훼손이 발생.
아주 드물게 나타나는 특이값, 오류(값 오류, 샘플링 오류)-
탐지 방법
- 시각화(산점도, Box plot또는, Histogram 등)
- 수치적 탐지방법(Box plot - IQR 기준)
- 확률이나 분포를 이용(Variance, Likehood)
- 기계학습 기법을 활용하는 기법(Nearest-neighbor, Density, Clustering)
-
처리방법
-
Tukey : 기준은 Q1, Q3 : 상한,하한을 벗어나는 값을 이상값으로 간주, 제거 가능
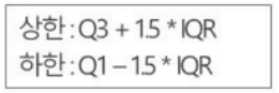
-
Carling : 기준은 중앙값 (Media) : 상한,하한을 벗어나는 값을 이상값으로 간주, 제거 가능

-
-
정규분포와 비교
-
-
잡음
: 데이터에 오류가 포함된 경우- 탐지방법
- 중복 : 동일한 데이터가 다른 이름으로 존재할 때 또는 동일한 이름의 데이터가 있을 때
- 속성값 차이 : 동일한 내용을 다른 형태로 저장하고 있을 때 (ex 1, 일)
- 상관분석 : 상관계수가 1에 가깝다면 중복데이터가 아닌지 확인
- 데이터 레벨의 차이 : 나이가 30살 차이가 나는 것 vs 통장 잔고가 30원 차이가 나는 것
- 처리방법
- 구간화 (Binning or Bucketization) : 데이터 값을 구간화하고, 각 구간의 평균값, 중앙값, 경계값 등을 구간값으로 사용하여 평활화는 기법, **필기/실기에서 빈출 처리 기법
- 회귀 (Regression) : 회귀함수에 의해 데이터를 평활화하는 기법
- 군집화 (Clustering) : 유사한 값끼리 그룹화하여 군집의 센터값을 이용하는 기법
- 탐지방법
통합 및 축소
결합
- 결합
테이블 구조를 가진 데이터 간에 공통 요소(컬럼 혹은 변수) 기준으로 둘 혹은 그 이상의 데이터 테이블을 합하여 하나의 데이터로 만드는 것.
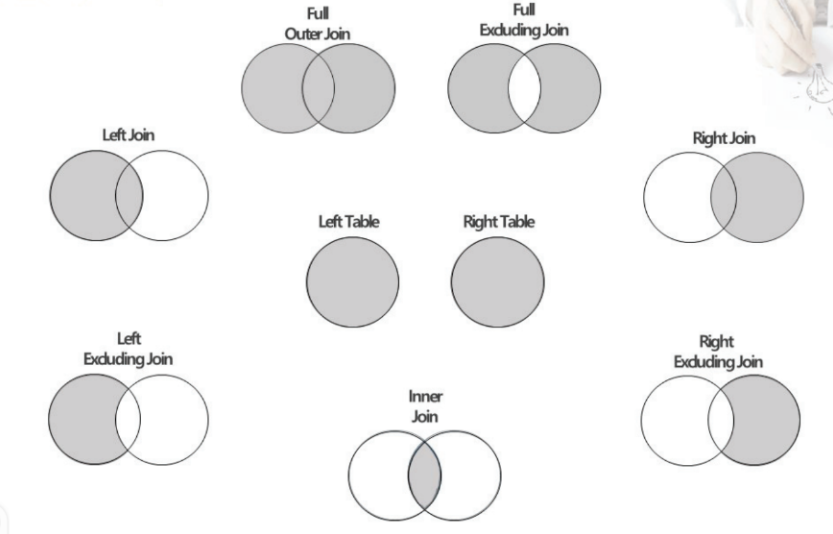
축소
- Flitering : 필요한 데이터만 추출하는 것.
- Sampling : 데이터의 양이 너무 많아 분석의 어려움이 있거나 시간 관점에서 현실적이지 않을 때 분석에 적정하게 조절
- 차원 축소 : 차원의 저주(Curse of Dimensionality)를 처리하기 위한 기법
- 차원의 저주 : 데이터의 차원이 늘어날수록 해당 공간의 크기가 기하급수적으로 증가하고 데이터의 밀도는 희박에지므로 데이터 분석에 필요한 데이터 수는 기하급수적으로 증가하게됨.
표본 추출(Sampling)
-
표본의 요건 : 모집단을 대표해야함
- 표본의 크기가 클수록, 모집단에서 골고루 추출될수록 표본의 대표성은 커짐
- 무작위로 추출하는 것은 이런 편향성을 배제하기 위함.
-
표본 오차(Sampling Error)
- 모집단을 모두 조사하지 않고 일부의 표본만 조사하기 때문에 발생되는 오차
- 표본 크기가 커질수록 작아지며 전수조사 시 0이 됨. -> 이런 이유로 데이터 분석 시 표준오차가 작은 값을 선택하는 의사결정을 하게 됨.
-
표본추출의 방법 : 4가지 구분하고 특히 층화, 집략추출 공통/차이점에 대해 기억해둘 필요가 있음
-
- 단순 임의 추출 (Sinple Random Sampling)
- 전체에 대해 무작위로 추출
- 난수표를 이용하여 표본의 크기만큼 개체를 선택
-
- 층화 추출
- 데이터 내에서 지정한 그룹별로 지정한 비율만큼 데이터를 임의로 선택
- 모집단의 각 층의 비율만큼 추출
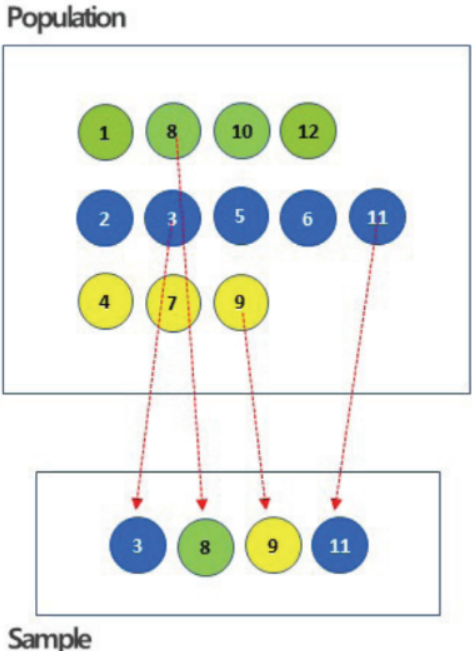
-
- 계통 추출(Systematic Sampling)
- 첫 번째 요소는 무작위로 선정하고 목록의 매 k번째 요소를 표본으로 선정하는 표집 방법
- 만약 표본이 추출되기 전 요소들의 목록이 무작위로 되어 있지 않고 주기성(periodicity)를 띄고 있다면, 계통 추출법을 통해 추출된 표본은 매우 어긋난 표본이 될 수 있으며 모집단을 전혀 반영하지 못하게 됨.
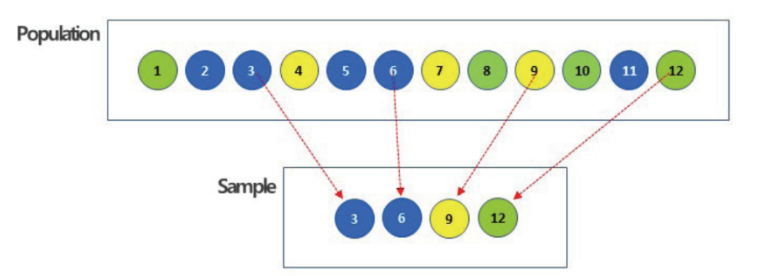
-
4, 집략 추출(Cluster Sampling)
- 소집단 자체를 표본대상으로 함.
- 군집 간 동일성, 군집 내 이질성인 경우 사용. (ex 백화점 등 지점/지역별 큰 차이가 없다면 한 지점을 선택해 전체/표본 추출)
- 장점으로는 군집을 잘 규정하면 비용이 절감되고, 군집의 특성을 평가하고 모집단의 특성과 비교할 수 있음
- 단점으로는 단순임의추출법보다 군집을 과대 또는 과소 평가해서 표본오차를 계산하기 어려울 수 있음
-
변환
모양 변환
- Pivot : 행,열별 요약된 값으로 정렬해서 분석하고자 할 때 사용
- Unpivot : 열(Column) 형태로 되어있는 것을 행 형태로 바꿀 때 사용
파생변수 생성
- 파생변수
- 이미 수집된 변수를 활용해 새로운 변수를 생성하는 경우
- 분석자가 특정 조건을 만족하거나 특정 함수에 의해 값을 만들어 의미를 부여한 변수. '주관적'일 수 있으며 논리적 타당성을 갖추어 개발해야함. (ex 인기매장, 구매다양성)
- 요약변수 : 빈도를 카운트한 개념
- 원데이터를 분석 니즈에 맞게 종합한 변수
- 데이터의 수준을 달리하여 종합하는 경우가 많음 (ex 총 구매금액, 매장별 방문 횟수)

정규화(Normalization)
- 개념
- 데이터의 속성값이 정해진 구간 내에 들도록 하는 기법
- Scale이 다른 여러 변수에 대해 Scale을 맞춰 모든 데이터 포인트가 동일한 정도의 중요도로 비교되도록 함
- 단위 차이, 극단값 등으로 비교가 어렵거나 왜곡이 발생할 때 표준화하여 비교 가능하게 만듬.
- 방법
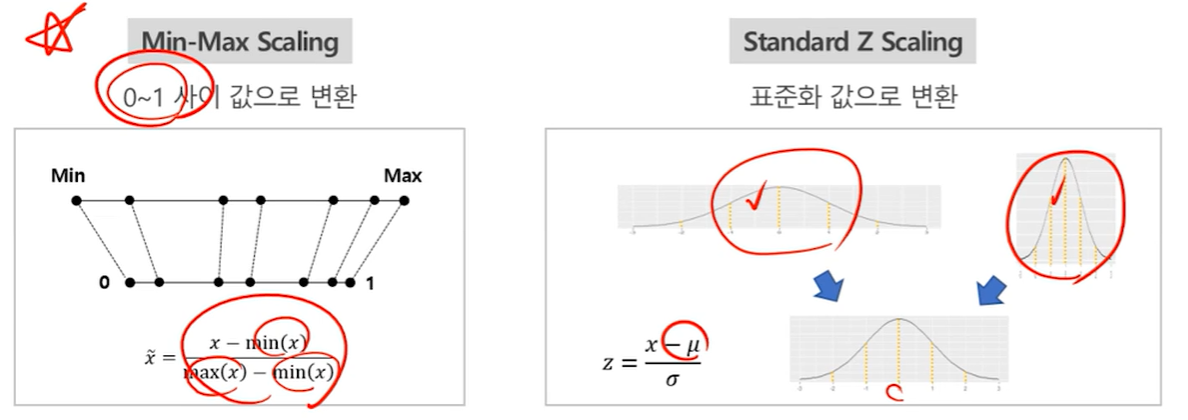
- Min-Max변환 : 0~1 사이 값으로 변환
- Z-score 변환 : 표준화 값으로 변환(ex 표준정규분포)
데이터 분포의 변환
-
개념
입력 데이터가 정규를 따르지 않는 경우, 정규분포 혹은 정규분포에 가깝게 변환하는 기법 -
방법
-
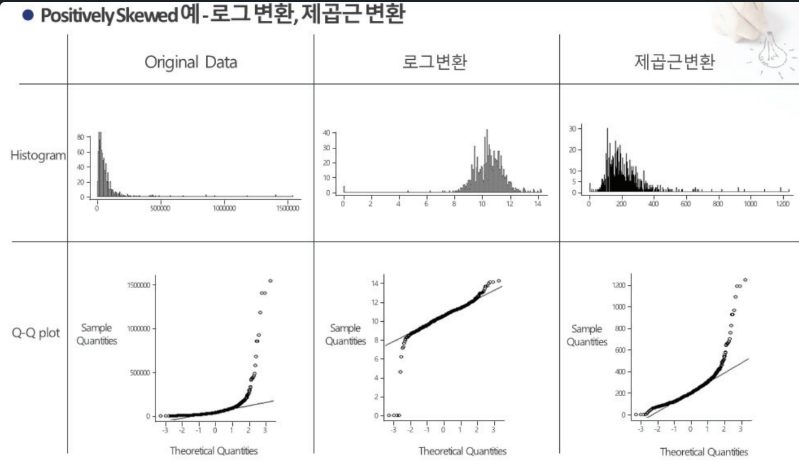
Positively Skewed (오른쪽 꼬리 긴 그래프) : Sqrt(x) -> log10(x) -> 1/x
-
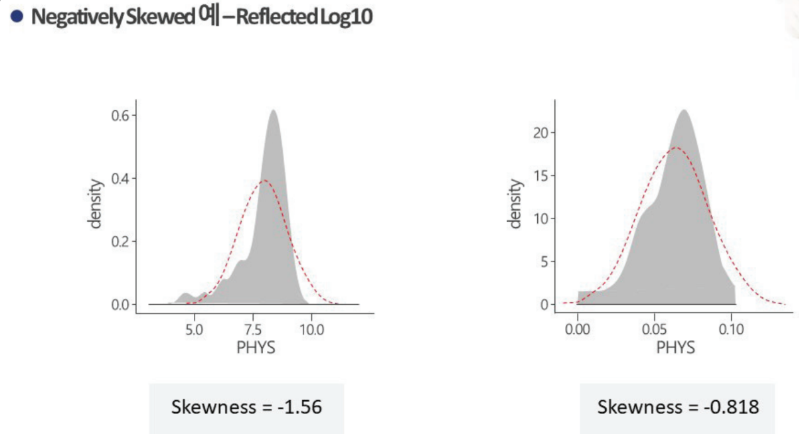
Negativly Skewed (왼꼬리 긴 그래프) : log변환
-
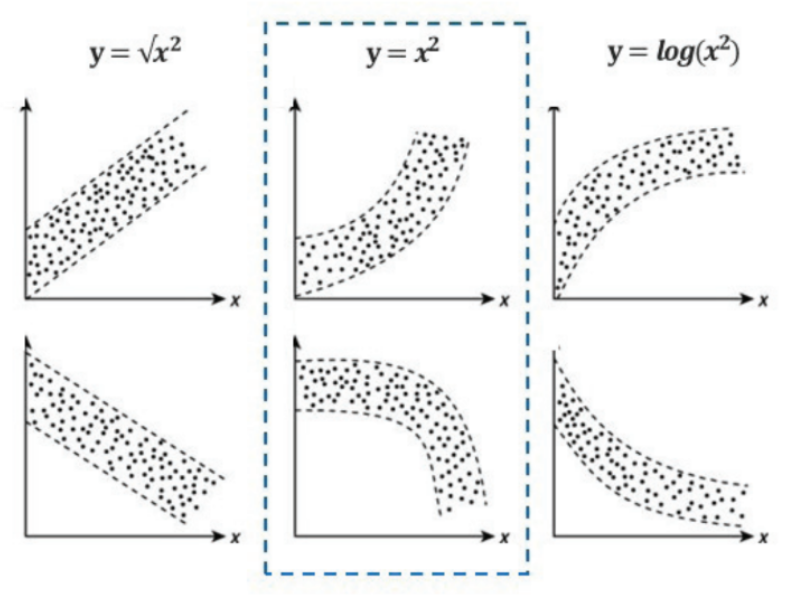
종속변수 증가가 독립변수 증가보다 급격할 때 : log변환 시도
-
종속변수 감소가 독립변수 증가보다 급격할 때 : 제곱(square)변환 시
-
-
