머신러닝
머신러닝 개요 및 유형
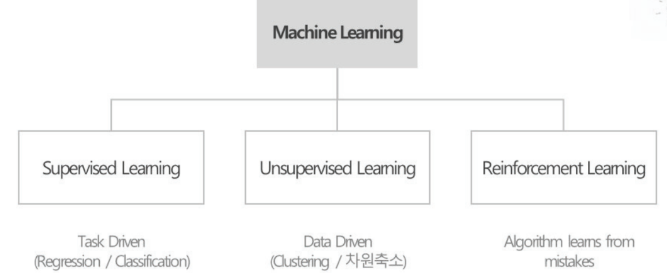
머신러닝(Machine Learning)
-
-
머신러닝 종류
- 지도학습(Supervised Learning)
- 학습 데이터 안에 입력값에 대한 출력값이 함께 제시됨
- 알고리즘은 입력값과 출력값 사이의 관계를 가장 잘 설명할 수 있는 "모델"을 찾고 이를 사용하여 새로운 입력값에 대한 예측 수행
- 출력값이 수치형인 회귀와 범주형인 분류 문제로 나누어짐
- 비지도학습(Unsupervised Learning)
- 학습 데이터 안에 출력값이 없음
- 알고리즘은 학습 데이터의 특징만을 활용하여 목표한 결과를 산출, 적절한 군집을 찾거나 변수의 복잡성을 낮추기 위한 자원 축소 등이 포함
- 지도학습(Supervised Learning)
-
일반적인 ML Steps
- Collect data : 유용한 데이터를 최대한 많이 확보하고 하나의 데이터 세트로 통합 (1.데이터 결합)
- Prepare data : 결측값, 이상값, 기타 데이터 문제를 적절하게 처리하여 사용 가능한 상태로 준비 (2.결측값 또는 이상값 탐지 및 처리)
- Split data : 데이터 세트를 학습용과 평가용 세트로 분리 (3.Train, Test 데이터 분리)
- Train a model : 이력 데이터의 일부를 활용하여 알고리즘이 데이터 내의 패턴을 잘 찾아 주는지 확인
- Test and validate a model : 학습 후 모델의 성능을 평가용 데이터 세트로 확인하여 예측 성능을 파악 (4. 학습용 데이터로 모델 생성 -> 평가용 데이터를 생성한 모델에 넣어 성능 확인)
- Deploy a model : 모델을 의사결정 시스템에 탑재/적용
- Iterate : 새로운 데이터를 확보하고 점증적으로 모델을 개선
특성공학 : Under/Over fitting
특성 공학(Feature Engineering)
- 개념
원시 데이터를 다루고 있는 문제를 더 잘 표현할 수 있는 특징(Feature)으로 변환하는 과정 - 중요성 : 단순한 모델로 좋은 성능을 낼 수 있다
- Feature
- 대상 문제에 유용하거나 의미 있는 특징
- Feature의 중요도를 객관적으로 측정할 수 있고 그 크기에 따라 모델에 포함하거나 제외할 수 있음
- 상관계수, 회귀계수와 p-value, 의사결정나무의 feature importance
- 방법
- Feature Selection
- Forward Selection 또는 Backward Elimination
- Feature Extraction
- Raw 데이터에서 새로운 데이터 만드는 개념
- 자동화 과정이다.
- vs Feature Construction
- Raw데이터에서 새로운 데이터 만드는 개념
- 수작업이다.
- vs Feature Learning
- Raw데이터에서 새로운 데이터 만드는 개념
- 비지도학습
- 정규화(Regularization)
beta(파라미터)값에 제약을 줌으로서 모델을 정규화. 일반성을 띄게 해준다. : feature의 영향을 줄이는 방법.
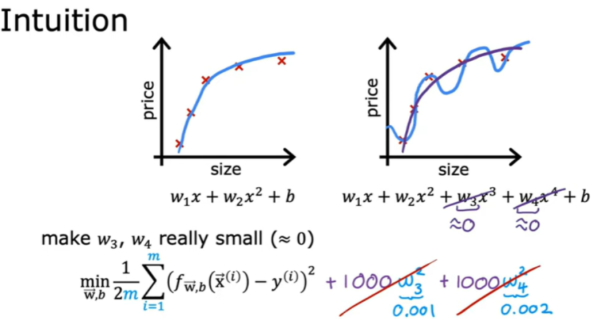
- Feature Selection
Underfitting
- 모델의 복잡도
- 입력변수가 증가하면 모델 복잡도 증가
- 출력변수의 가능한 class가 늘어나면 모델 복잡도 증가
- 입력변수와 출력변수 간 관계가 비선형적이면 모델 복잡도 증가
- 개념 : 주어진 입력 데이터에 비해 모델의 복잡도가 너무 낮아 입력 데이터로부터 충분히 학습하지 못하는 상황 (모델이 너무 단순해 정답을 잘 못 맞추는 것) : High bias
- 대응방법
- 학습 시간을 늘린다
- 더 복잡한 모델을 구성한다.
- 모델에 추가 Feature를 도입한다
- Regularization을 사용하지 않거나 영향을 줄인다
- 모델을 다시 구축한다
Overfitting
- 개념 : 주어진 입력 데이터에 비해 모델의 복잡도가 너무 높아 입력 데이터의 잡음까지 fitting하는 경향을 보이고 일반화에 실패하는 상황 : High variance
- 대응방법
- 학습을 더 일찍 멈추게 한다
- 데이터를 추가한다
- 모델의 복잡도를 낮춘다
- 일부 feature를 제거한다
- Regularization을 활용한다.
특성공학 : 모델평가기법
Data Split과 모델 검증,선택,평가
- Hold-Out
- 데이터를 두 개 세트로 나누어 각각 Train과 Test set으로 사용
- 7:3~9:1가 일반적이나 알고리즘 특성,상황에 따라 적절 비율 사용. Train-Validation-Test로 나누기도 함
- Cross Validation (교차검증)
- 전체 데이터 세트를 임의 k개 그룹으로 나누고, 그 가운데 하나의 그룹을 돌아가면서 테스트 데이터 세트로, 나머지 k-1개 그룹은 학습용 데이터 세트로 사용하는 방법
- 일반적인 모델 선택 과정
- 여러 모델을 대상으로 Cross Validation을 수행
- 가장 좋은 결과를 낳은 하나 / 소수의 모델 선택
- 학습 데이터를 모두 사용하여 모델 생성
- 분리해 놓은 평가 데이터로 모델 평가
- 모델 평가
- 모델 평가에 가장 널리 사용되는 지표는 예측력
- 회귀 모델의 평가에는 오차의 크기
- 분류 모델의 평가에는 정확도 개념 사용
- 예측력이 유일한 지표는 아니며, 지표들이 독립적이지 않으므로 입체적인 고려가 필요
- 해석력 : 입력과 출력 간 관계를 잘 설명하는가
- 효율성 : 유사한 성능을 보이는 경우, 적은 입력 변수로 모델을 구축하는가
- 안정성 : 새로운 데이터 세트에도 같은 성능의 결과를 나타내는가
- 모델 평가에 가장 널리 사용되는 지표는 예측력
모델 평가 지표
-
회귀 모델
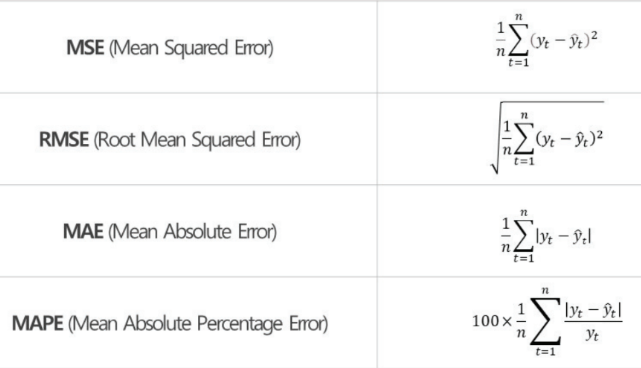
: 예측 대상이 연속형 수치 데이터인 경우- MSE : 에러 제곱의 평균
- RMSE : MSE에 루트
- MAE : 에러 절대값의 평균
- MAPE : MAE를 백분율로 표현한 것
-
분류 모델
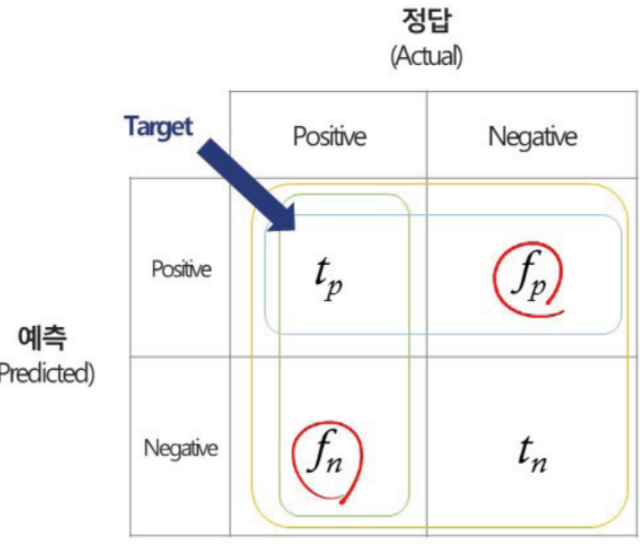
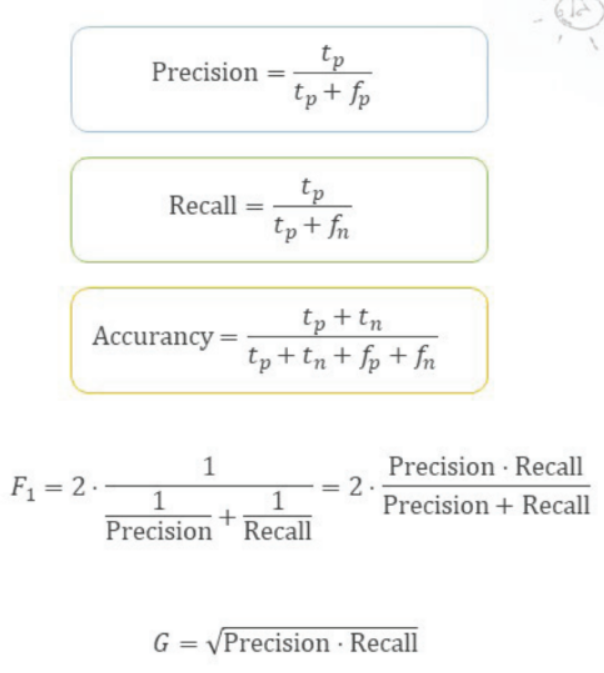
: 예측 대상이 범주형 데이터인 경우- Precision(정밀도) : 분류 모델이 Positive로 판정한 것 중 실제로 Positive인 샘플 비율
- Recall(재현율) : 실제 Positive샘플 중 분류 모델이 Positive로 판정한 비율
- Accuracy(정확도) : 전체 샘플 중 맞춘 비율
- F1-Score : Precision, Recall의 조화평균. 0~1사이 값이며 1에 가까울수록 분류 성능이 좋다.
-
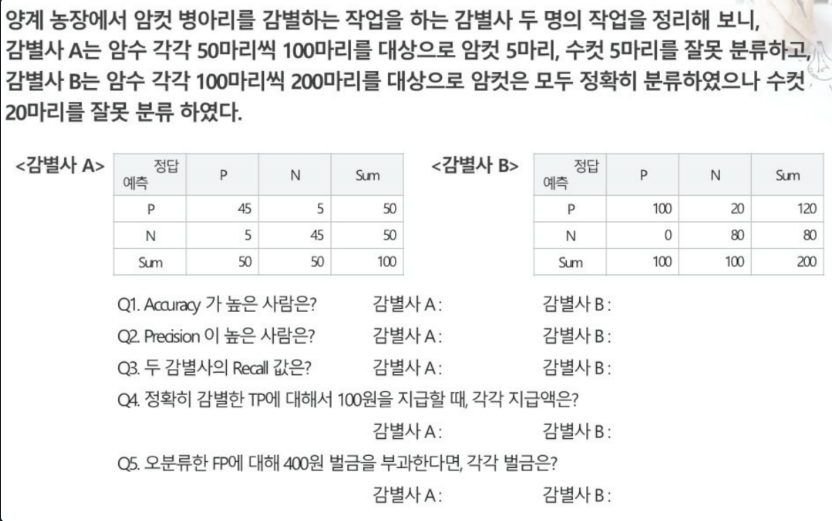
평가지표연습
-
선형회귀분석(머신러닝파트)
선형회귀 계수의 추정
- Regression : 한 변수를 다른 변수/변수들의 함수 관계로 표현하는것.
- Linear Regression(선형회귀분석) : 독립변수 X(1~n개) 로 종속변수 Y를 설명할 때의 관계가 선형 관계
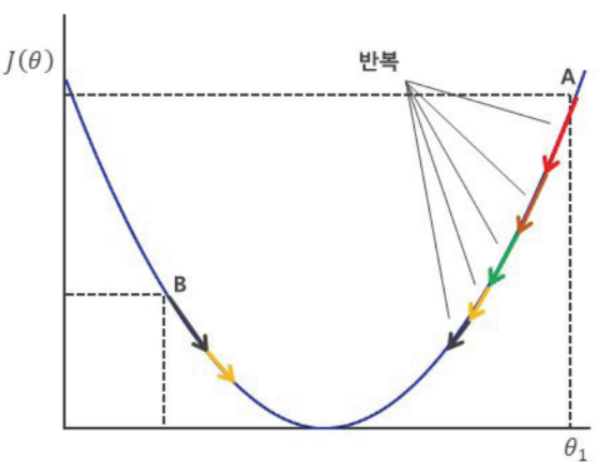
- Gradient Descent
- 임의의 시작점에서 Cost Function(손실 곡선)의 기울기를 계산,
- 기울기가 감소하는 방향으로 이동 후 다시 손실 곡선의 기울기 계산
- 일정 보폭(Learning Rate), 혹은 점차 감소하는 보폭으로 이동과 기울기 계산을 반복
- step(learning rate)가 크면 발산 위험이 있고, 너무 작으면 수렴이 느리거나 local optima에서 벗어나지 못할 수 있다.
다중공산성
- 개념 : 독립변수들 간 강한 상관관계사 존재하는 상태
- 다중공산성이 있을 때에는 독립변수와 종속변수 간의 영향 정도를 정확히 산출하지 못하는 현상이 나타남
- 확인 방법
- X변수들 간의 산점도나 상관계수를 보아 상관성이 높은지 확인
- VIF(Variance Inflation Factor)가 10 이상인 설명(독립)변수
- 해결방법
- 다중공산성이 있는 독립변수를 제거
- 주성분분석(PCA)를 통해 추출된 서로 독립인 주성분을 사용하여 회귀분석 수행
- Ridge나 LASSO 기법을 활용하여 가중치를 조정
회귀모형에서 명목형 번수의 처리
- One-Hot Encoding
- 열(Column)에 범주형 데이터의 항목을 추가하고, 값을 수치(0또는1)로 표시하는 것
- Dummy Variable (or Index Variable)
- One-Hot Encoding의 단점인 컬럼이 증가하게 됨
- 기울기 추정이 불가능해지고, 이를 보완하기 위해 1개의 항목을 제거하는 것을 Dummy화 라고 함.
Penalized Regression
-
변수 많은 경우 최적의 회귀 계수 추정이 어려우므로 사용된 변수 선택 기법 (forward selection, backward selection)
-> 변수 선택 과정이 비연속적 방법으로 고차원의 상황에서 최적의 변수 집합 찾는 것 확신 불가 -
Penalized Regression : 벌점화 회귀 , 모델 평가 기준인 예측력과 안정성을 위해 기존의 비용 함수에 벌점함수를 더한 형태의 새로운 비용함수를 정의, 이러한 비용함수를 최소화하는 모수를 찾는 과정인 규제를 거침.
-
공통 원리로 SSE(잔차)에 Penalty를 더하여 [SSE+f(x)=penalty]를 함께 축소시키는 것을 목표로 함.
-
-
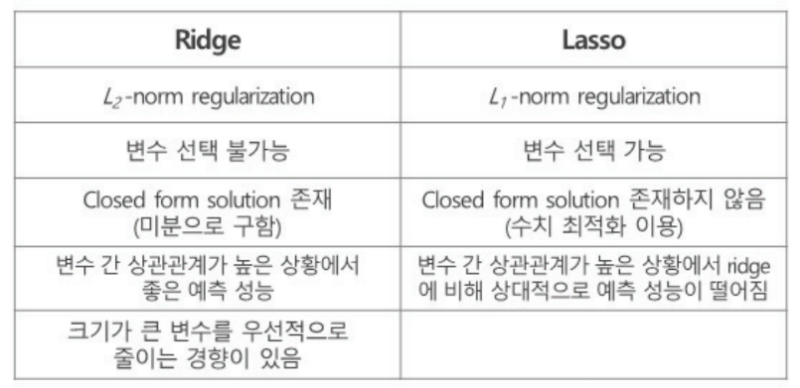
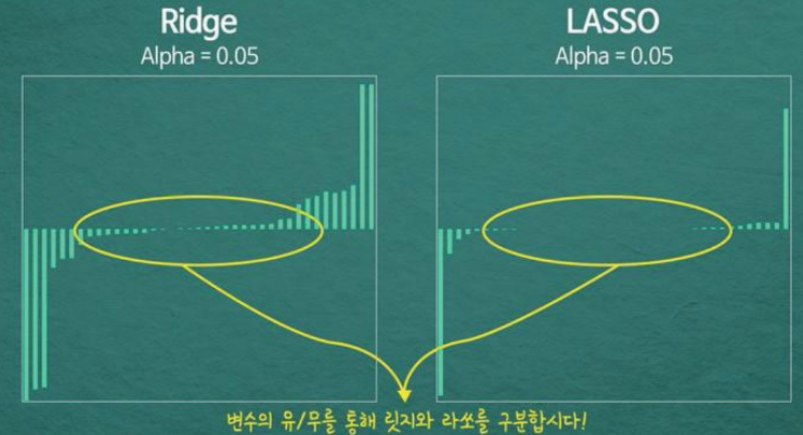
Ridge와 Lasso는 다중공산성을 정규화 시키는 방법
-
-
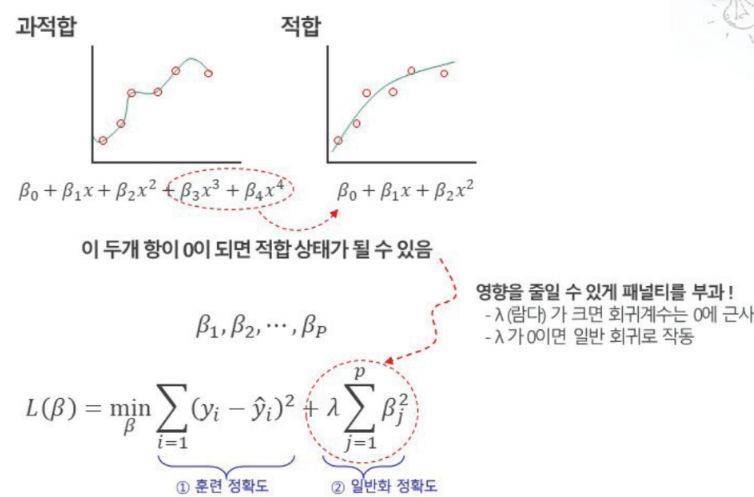
Ridge Regression : 과적합을 피하고 일반화 성능을 강화하는 방법 (L2 Norm Regularization)
- 다중공산성 관계가 있는 독립변수의 가중치를 조절
- 패널티 항 : 파라미터의 제곱의 합. 람다가 패널티를 조절하는 값.
-
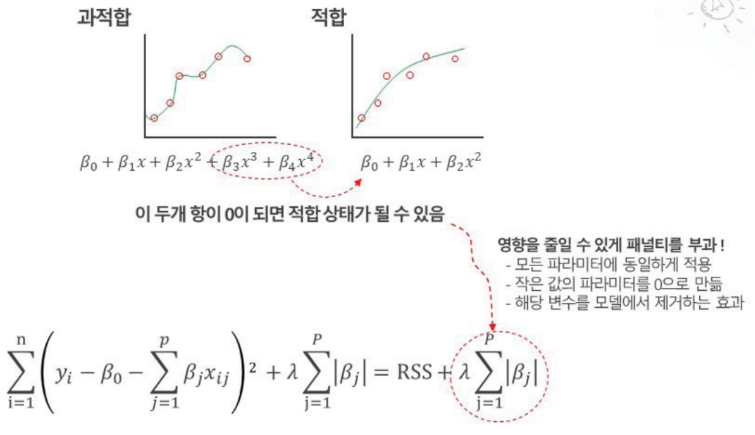
LASSO (Least Absolute Shirinkage Selector Operator) (L1 Norm Regularization)
- 다중공산성 관계가 있는 독립변수를 삭제
- 패널티 항 : 파라미터 절대값의 합. Ridge의 가중치들은 0에 가까워질 뿐 0이 되진 않지만, LASSO의 가중치들은 0이 된다. 특성이 많은데 그 중 일부만 중요하다면 LASSO가, 특성의 중요도가 전체적으로 비슷하다면 Ridge가 더 좋을 수 있다.
로지스틱 회귀분석
Classification
- Classification
- Supervised Learning의 일종
- 입력 데이터에 존재하는 Feature 값들과 label 값의 class간의 관계를 학습하여 새로 관측된 데이터의 class를 예측하는 문제
Logistic Regression
-
이진 분류
- Label 값으로 0/1, Y/N과 같이 두 가지 class만 가능
-
프로세스 개요
- 독립변수들(x)의 선형결합과 종속변수(y)의 class간 확률적 관계 학습
- Gradient Descent로 최적화된 coefficients와 intercept를 계산
* Threshold를 조절하여 positive class와 negative class를 어떻게 나눌지 설정 : y값을 확률로 가정. (0.5 기준으로 0/1 , Y/N..)
-
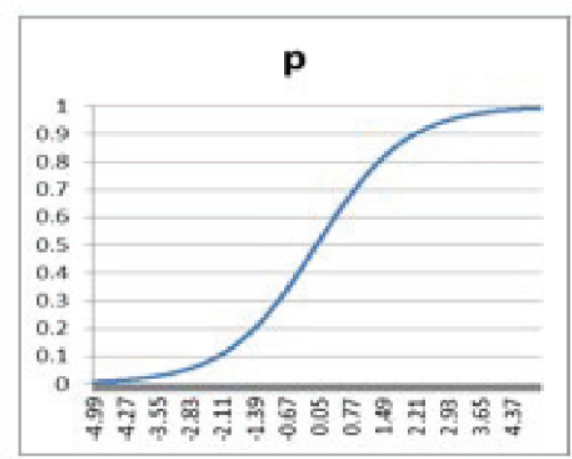
변환 과정
-
Odds(승산) (0~∞)
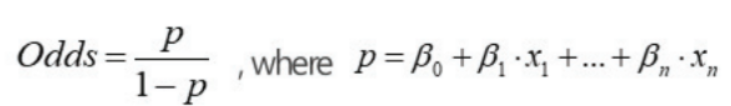
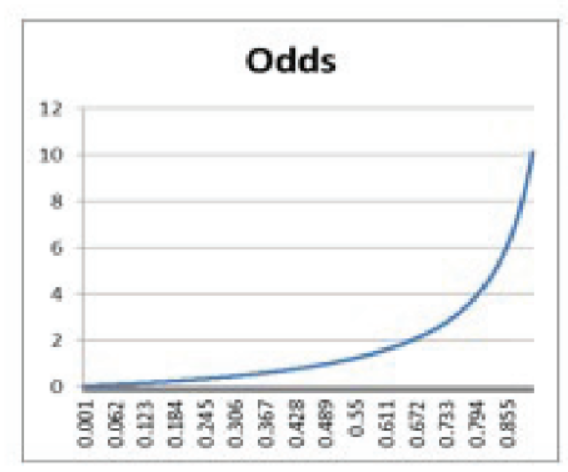
-
Logit(로짓) (-∞ ~ ∞)
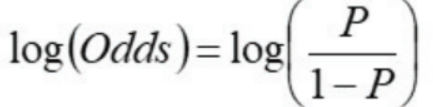
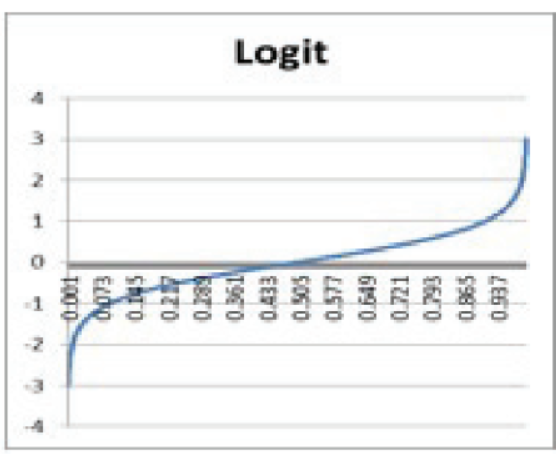
-
역함수 ( 0 ~ 1)
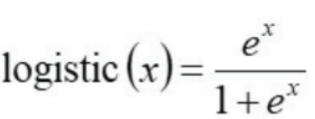
-
-
XOR문제
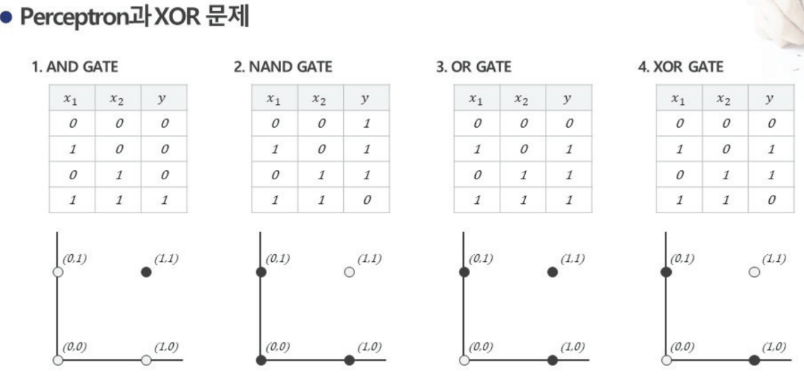
4번은 로지스틱 회귀분석 또는 선형분류모델로 볼 수 없다. -
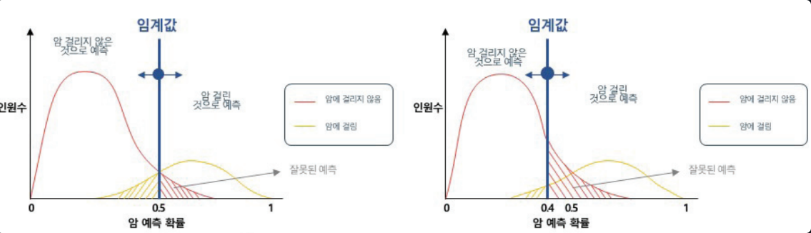
Thresholds
- T 기본 임계값은 0.5
- P(Y=1) >= 임계값 이면 1로 분류 / P(Y=1) < 임계값 이면 0으로 분류
- 임계값을 낮추면 Recall(민감도)가 높아져 오분류가 높아지더라도 Y=1인 경우를 최대한 분류
- 임계값을 높이면 Precision이 높아지게 되어 알파 오류를 최소화하는 경향이 있음
-
Regression과 비교
- 선형회귀
- 종속변수는 y값 자체
- 회귀계수는 해당 독립변수 값이 1단위 증가할 때 종속변수 y의 변화량
- 비용함수는 예측오차의 최소화
- 로지스틱 회귀
- 종속변수는 logit확률로부터 도출한 class 값
- 회귀계수는 해당 독립변수 값이 1단위 증가할 때 log(odds) 변화량
- 비용함수는 cross entropy의 최소화 혹은 log likehood의 최대화
- 선형회귀
-
ROC (Receiver Operating Characteristic) and AUC(Area Under the Curve)
-
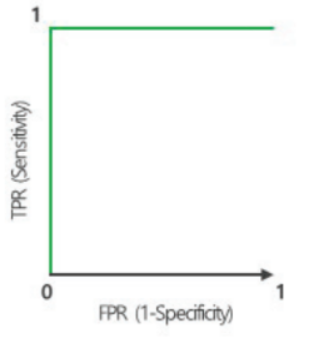
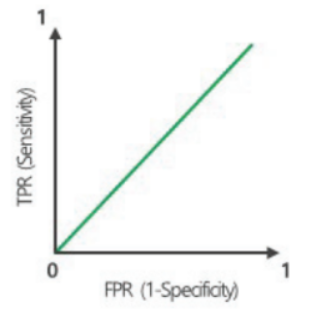
임계값 변경에 따른 분류 결과 변동의 Trade-off 상황을 그래프로 요약하여 보여줌
-
Negative 중 위양율(False Positive Rate)를 x축에, Positive 중 진양율(True Positive Rate)를 y축에 표시
-
특이도 감소 속도에 비해 얼마나 빠르게 민감도가 증가하는지 나타
-
AUC = 1이면, 분류기가 Positive와 Negative를 완벽하게 분리
-
AUC = 0.5이면, 분류기가 Positive와 Negative를 구분하지 못함. (무작위 임의 선택과 같은 수준)
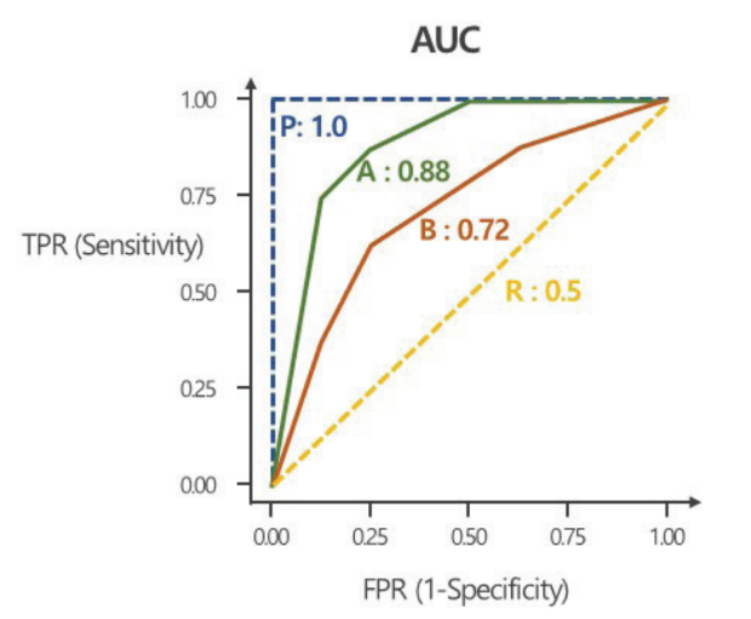
0.7~0.8정도면 fair, 0.8~0.9정도면 good, 0.9 초과 시 excellent
-
KNN 알고리즘
KNN
-
개념
- Test Data와 가까운 k개의 Train Data의 y값들을 비교
- k 값에 따라 예측 결과가 달라짐
- 동점을 막기 위해서 데이터가 적을 때에는 k값은 대개 홀수로 정함
-
활용 : 분류와 회귀 문제를 모두 다룰 수 있음.
- 분류 : 객체는 k개의 Nearest Neighborhood 사이에서 가장 공통적인 항목에 할당되는 객체로 과반수 의결에 의해 분류
- 회귀 : k개의 Nearest Neighborhood를 찾고 해당 이웃이 가지고 있는 값의 평균이 output값이 됨.
- k값이 1에 가까워질수록 Overffiting 걸릴 가능성이 높아지고 k값이 커질수록 모델은 단순해지지만 Underfitting 가능성이 생길 수 있다.
-
방법
-
1) 거리 측정
-
Minkowski distance (민코우스키 거리)
Euclidean 거리와 Manhattan거리의 일반화 형태
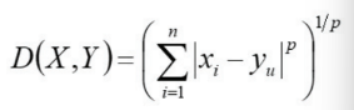
-
Euclidean distance (유클리디안 거리)
-
Manhattan distance (맨해턴 거리)
-
-
2) 표준화 검토
- 거리 개념을 사용하는 알고리즘의 경우 Normalization 사용을 항상 검토 필요
-
3) 정확도 검토
- k값의 변화에 따른 오분류는 일반성이나 경향성을 가지고 있지 않기 떄문에 최적의 k값을 찾는 것은 쉽지 않음. -> 따라서 k값을 변경하면서 error가 작은 것을 선택.
-
4) 장점
- 단순한 알고리즘으로 이해하고 해석하기 쉬움
- 데이터에 대한 기본 가정이 없으므로 비선형 데이터에 매우 유용
- 분류와 회귀 모두에 사용 가능하고 이상값 찾기에도 활용 가능
- 대체로 우수한 결과를 보여줌
-
5) 단점
- 상대적으로 높은 계산 비용
- 데이터 양이 매우 큰 경우 계산 속도가 느려지고 데이터의 지역 구조에 민감
- 최적의 k값을 정하는 것이 쉽지 않음
- k가 너무 작은 값이면 잡음에 영향을 받을 가능성(Overfitting)
- k가 너무 큰 값이면 지나치게 평활될 가능성(Underfitting)
-
예제
-
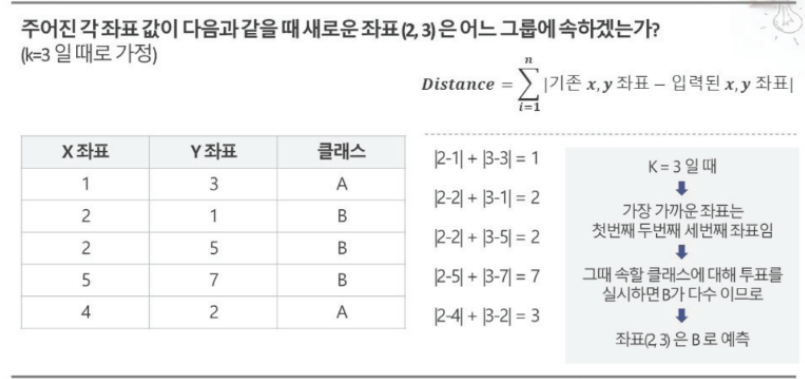
-
나이브베이즈
나이브 베이즈 분류
-
개념 : Bayes 법칙에 기반한 분류 기법
-
독립성을 가정한 기법 : Feature들이 모두 동등하게 중요하며 독립적이라는 가정, 이 가정사항이 다소 비현실적이어서 Naive라는 표현을 사용한다.
-
Bayse Theorem (베이즈 정리)
-
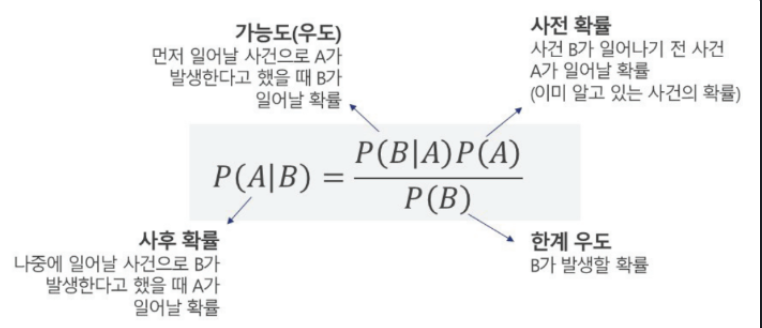
-
Laplace Smoothing
- zero frequency문제 : 학습 데이터 중 a단어가 나타나지 않았다면 확률을 0 취급함. : 특정 상수를 더한다. (1또는 0.5 자주 사용)

- zero frequency문제 : 학습 데이터 중 a단어가 나타나지 않았다면 확률을 0 취급함. : 특정 상수를 더한다. (1또는 0.5 자주 사용)
-
UnderFlow
- 아주 나타날 확률이 작은 경우 컴퓨터 연산 범위 넘는 현상 발생 가능.
: exp와 log 활용
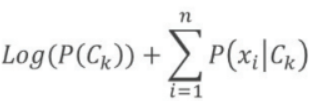
- 아주 나타날 확률이 작은 경우 컴퓨터 연산 범위 넘는 현상 발생 가능.
-
Feature 개수가 증가 시 기하급수적으로 많은 데이터 필요함
- 변수 개수 n개라면 최소 2^n개 데이터 필요함. -> 이로 인해 독립이라는 가정 필요
-
-
-
활용 : 스팸메일필터링 등 텍스트분석 / 비정상 행위 탐지/ 일련 관찰 증상에 대한 의학 질병 진단
-
장점
- 가장 단순한 지도 학습 방법 가운데 하나로 빠르고 정확한 모델
- 적은 량의 데이터로도 좋은 정확도를 보여줄 수 있음(잡음,누락 등에 강함)
- 대량 데이터 세트에서도 빠른 속도를 나타냄
- 연속형 데이터 보다는 이산형 데이터에서 높은 성능
- 멀티클래스에도 사용 가능
-
단점
- 각 Feature끼리 서로 독립이라는 조건을 가정하나, 현실적으로 독립성 가정 대부분 위배.
- 모든 특징이 동등하게 중요하게 간주
- 연속성 수치 데이터가 많은 경우 이상적이지 않음 -> 이산화 필요
- 조건부 확률이 0이 되는 문제 존재 (방지 위해 상수항 사용)
- 데이터 사이즈가 작으면 Overfitting 가능
-
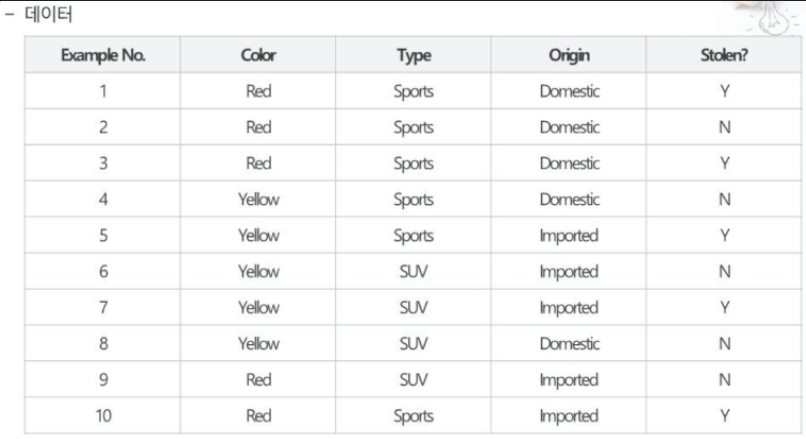
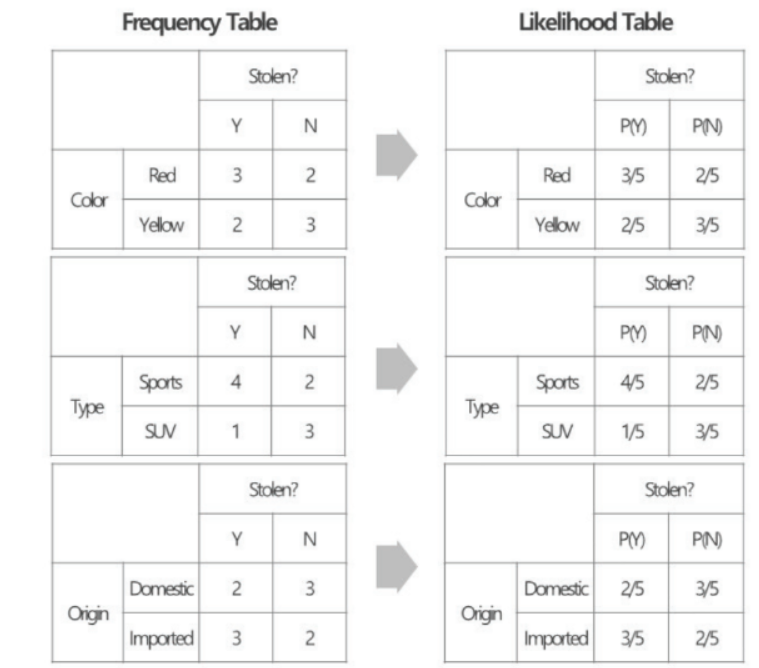
예제
의사결정 나무
의사결정 나무(Decision Tree)
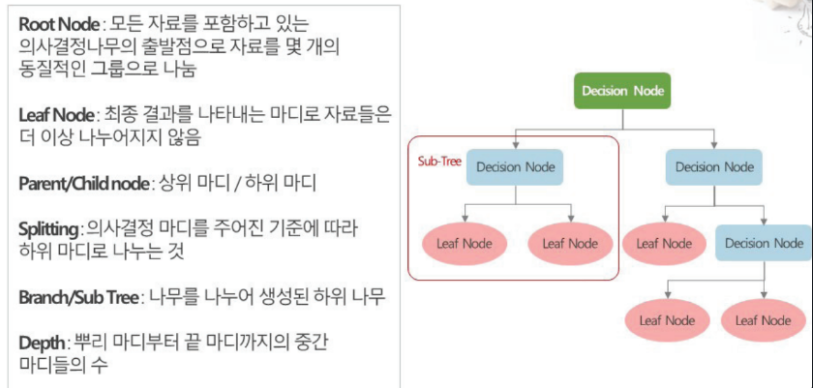
- 개념 : 의사결정 규칙을 나무 구조로 도식화하여 관심대상이 되는 집단을 몇 개의 소집단으로 분류하거나 회귀하는 예측 방법
- 구조와 용어
- 타입
- 분류 나무
- 범주형 목표 변수를 기준으로 마디를 나눔
- 끝마디에 포함된 자료의 범주가 분류 결과 값이 됨
- 회귀 나무
- 연속형 목표 변수를 기준으로 마디를 나눔
- 끝마디에 포함된 자료의 평균값이 각 끝마디의 회귀 값이 됨
- 분류 나무
- 장점
- 시각화를 통한 쉬운 이해
- 자료 가공이 거의 필요 없음
- 수치형 및 범주형 데이터 모두 적용 가능
- 선형성, 정규성 등의 가정이 필요 없는 비모수적 방법
- 대량 데이터 처리에도 적합
- 단점
- 휴리스틱에 근거한 실용적 알고리즘으로 전역 최적화를 얻지 못할 수 있음
- 과적합이 쉽게 발생하며 자료에 따라 불안정.
- Feature 간 복잡한 관계를 처리하지 못함
- 자료가 복잡하면 실행 시간이 급격히 증가
- 알고리즘의 특성
- 불순도를 감소시키는 방향으로 분리 ( select feature & split -> Brute force로 각 변수별 값 바꾸어가며 불순도 비교.)
- 프로세스
- 1) 모든 자료를 포함한 root node로 부터 시작한다
- 2) 자료 가운데 불순도를 낮추는 최적의 요인을 찾는다
- 3) root node를 최적 요인의 기준값을 찾아 하위 그룹으로 나눈다
- 4) 각 하위 그룹에 대한 의사결정나무의 node를 만든다.
- 5) 3,4과정을 더이상 node를 나눌 수 없을 때 까지 혹은 정지규칙에 해당할 떄까지 반복한다.
- 불순도(Impurity Measure)
- 지니 불순도(Gini Impurity) : 최대값 0.5
- 엔트로피(Entropy) : 최대값 1
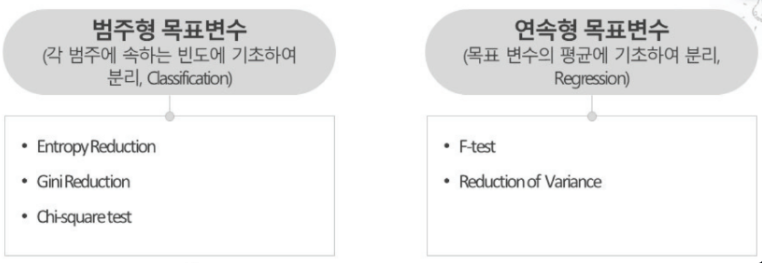
- Gini Impurtiy와 Entropy 값이 0에 가까울 수록 분류가 잘 된 것
- 정보 획득량 (Information Gain, IG) = Gini(parents) - {p(C1) Gini(C1) + p(C2) Gini(C2)}
- Overfitting : 학습 데이터에 대해서는 좋은 결과를 내나, 새로운 데이터에 대해서는 정확한 예측을 하지 못하는 경우
- 학습데이터가 부족한 경우
- 학습데이터에 잡음이 있는 경우
- 학습데이터에 너무 특화되는 상황
- 정지규칙
- 모든 마디가 순수한 상태가 되면 정지
- 의사결정나무가 완전히 다 자라기 전에 정지하도록 하여 과적합을 방지하거나 지나치게 긴 실행시간을 제한할 수 있음
- 트리의 깊이(depth)가 지정한 값(Max Depth)에 도달함
- 노드의 크기가 지정한 값(Min Instance Per Node)보다 작음
- 불순도의 감소량이 지정된 값(Min Information Gain)보다 적음
- 가지치기
- 의사결정나무가 끝까지 자라도록 한 후 상향식으로 가지치기 실행
- 모델은 단순해지면서 성능이 덜 떨어질 때 까지 잘라본다. 자를수록 데이터는섞이지만 많은 쪽으로 Label을 정함.
- 의사결정나무가 끝까지 자라도록 한 후 상향식으로 가지치기 실행
- 중요 Variables
- Tree 상단에서 사용
- 자주 사용
- 혼잡도 개선 효과가 높은 것
군집분석 개요
비지도 학습(Unsupervised Learning)
- 개념 : 입력 데이터에 Label이 없이 데이터의 특징 만으로 패턴을 찾는 학습 방법
군집 분석은 비지도 학습 중 하나로 지도 학습과 차이점 위주로 특징 기억해야한다. - 비지도 학습 활용 사유
- Label이 되지 않은 데이터가 더 확보하기 쉬움
- 잘 알려지지 않은 모든 종류의 패턴을 찾어려는 시도
- 범주화에 도움이 되는 특징과 패턴을 알아내는데 도움이 됨
- 새로움 데이터에 대한 실시간으로 처리가능
- 종류 : Clustering, Association Rule, Dimentsion Reduction
군집 분석(Clustering)
- 개념
- 주어진 입력 값을 바탕으로 유사한 값들로 데이터를 몇 개의 그룹으로 묶어주는 것
- 각 집단의 성격을 파악하여 데이터 전체의 구조에 대한 이해를 높이는 탐색적 분석방법
- 특징
- 사전에 정의되거나 가정하는 사항 없이 데이터에 의존하는 분석 기법으로 분석가의 해석이 중요
- 점포 세분화, 고객관리를 위한 구분, 가맹점 세분화 등에 널리 활용됨
- 하나의 유일한 답이 존재하는 것은 아님
- 데이터 안에서 찾고자 하는 것, 강조하고자 하는 것에 따라 달라질 수 있음
- 때로는 Clustering 알고리즘보다 유사도를 어떻게 정의하는가가 더 중요할 수 있음.
- 거리(Distance)
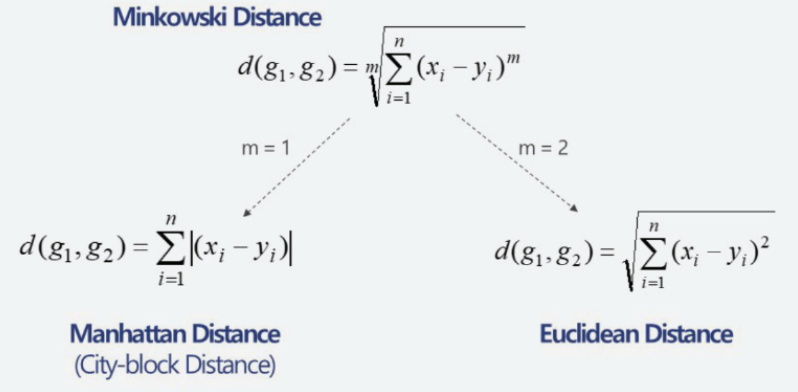
- Euclidean Distance
- 다차원의 실제 값을 기반으로 계산
- m- 차원 공간의 두 지점 사이의 거리
- 두 지점 사이의 평균과 같은 개념을 가지고 있음
- Manhattan Distance
- Euclidean Distance
- 표준화 : 거리 계산을 해야하므로 분석 전 스케일을 맞추는 전처리를 진행해야 한다.

- Min-Max Scaling : 최대값, 최소값을 0~1 scale로 조정
- Z-Score/Standard Scaling : 정규화 z-score로 변경
- Robust Scaling
- Max-Absolute Scaling
비계층적 군집분석
비계층적 군집분석(Non-hierachical Clustering)
- 접근법
- 주어진 데이터를 k개의 군집으로 나눔
- 원하는 군집의 수 k를 사전에 지정 (알고있다 가정 : 계층적 군집분석 면저 수행하고 대략적인 k를 유추하고 진행한다.)
- k-평균 군집화(k-means clustering) 알고리즘
- 군집의 중심이 되는 k개의 Seed 점들을 선택하여 seed 점과 거리가 가까운 개체들을 그룹화하는 방법
- 1) k개의 중심점을 임의로 배치
- 2) 모든 자료와 k개의 중심점과 거리를 계산하여 가장 가까운 중심저의 군집으로 할당함
- 3) 군집의 중심을 구함(평균을 구함)
- 4) 정지 규칙에 이를 때까지 2~3단계를 반복
- 군집의 변화가 없을 때
- 중심점의 이동이 임계값 이하일 때
- 왜곡값(distortion) : 왜곡값은 작을수록 좋다
- 군집의 중심이 되는 k개의 Seed 점들을 선택하여 seed 점과 거리가 가까운 개체들을 그룹화하는 방법
K-means Clustering
- 클러스터 개수(k) 선정
- 클러스터 개수 k를 사전에 정해야 하며 결과는 k값에 크게 영향 받음.
- 다른 k값을 이용한 시뮬레이션을 통하여 최선의 선택 시도
- 클러스터 개수 선정
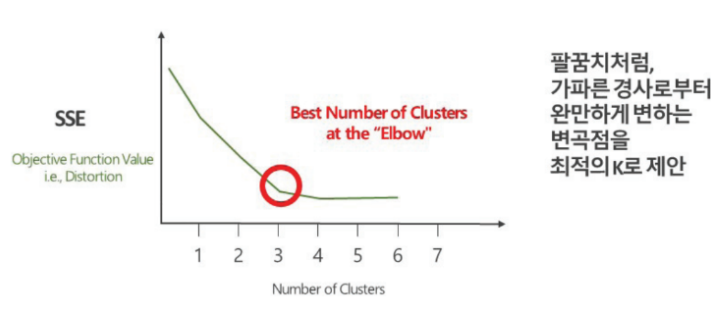
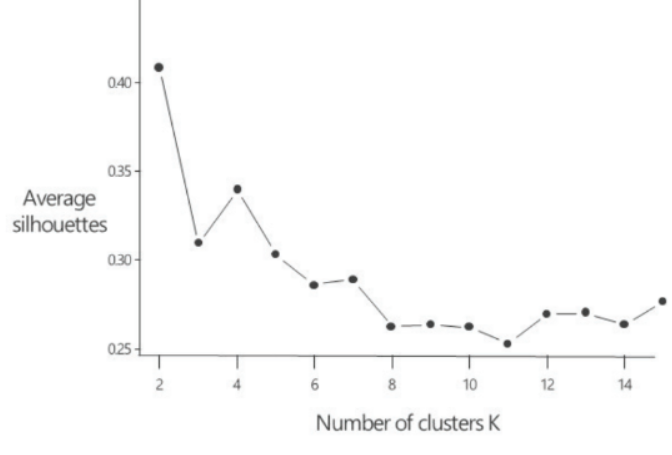
- Elbow Method
- Silhouette coefficient Method : 모든 개체에 대한 Silhouette 값을 계산, 확인하고 클러스터별로 그 값의 분포를 검토하는 방식으로 유효성 검토
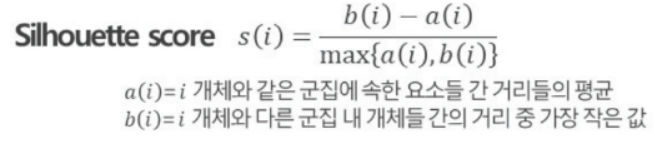
- 군집 대상에 대한 적절한 정보와 이해가 필요
- 적정한 K값을 지정하기 위한 다양한 시도가 요구됨.
- 항상 판별이 용이한 팔꿈치가 제시되는 것은 아니기 때문에 Elbow Method와 Silhouette Method를 같이 쓰는것을 권장
- Elbow Method
- 장점
- 대용량데이터에 대한 탐색적 분석
- 적용이 용이하고 수행이 빠름
- 언제나 Cluster가 나누어짐
- 단점
- 최소 지역 최적화는 달성하지만, 전역 최척화는 장담하지 못함
- 의미 없는 Cluster가 형성될 수 있음
- 결과 해석이 어려움
- 목적에 맞는 변수를 제공해야 함
- 이상값에 민감
- 예제
- 장/단점은 잘 출제됨 비계층적 군집분석 뿐 아니라 머신러닝 기법별 장/단점은 잘 구분해 기억해둘 것. 머신러닝 계산문제도 마찬가지.