순차탐색
- 정렬되어 있지 않은 배열에서 차례대로 탐색
- 평균적으로 (n+1)/2번의 비교, 최악의 경우 n번 비교
- 시간 복잡도 O(n)
이진탐색
- 정렬 되어있는 데이터에서 특정 값을 찾아내는 알고리즘
- 중간값 선택해서 탐색 범위를 반으로 나눠 범위를 좁혀가는 방식
- O(log n) 탐색 속도 보장
정렬
- 데이터를 특정 순서대로 나열하는 알고리즘
- 선택정렬, 삽입정렬, 퀵정렬, 계수정렬 등
이진트리
- 각 노드가 최대 2개의 자식 노드를 가질 때
- 이진 탐색 트리는 정렬된 이진 트리임
- 왼족 자식 노드 < 부모 노드 < 오른쪽 자식 노드
떡볶이 떡 만들기
문제

풀이
이진 탐색 문제
떡의 최대 길이를 구해 반으로 잘라가며 잘라 남은 길이가 총 만들어야 하는 M보다 큰지, 작은지 구한다.
떡 길이가 총 길이 M보다 크거나 같은 경우 더 크게 잘라도 된다는 뜻으로 start를 mid + 1로 높이고
떡 길이가 총 길이 M보다 작을 경우 더 작게 잘라도 된다는 뜻으로 end를 mid - 1로 낮춘다.
package _240628;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
// 자를 높이의 range가 중요. 이 range를 이진탐색으로 처리
public class 떡볶이떡만들기 {
static int N, M, ans=0;
static int arr[];
public static void main(String[] args) throws Exception {
BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer stringTokenizer = new StringTokenizer(bufferedReader.readLine());
N = Integer.parseInt(stringTokenizer.nextToken());
M = Integer.parseInt(stringTokenizer.nextToken());
arr = new int[N];
int end = 0, start = 0;
stringTokenizer = new StringTokenizer(bufferedReader.readLine());
for (int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(stringTokenizer.nextToken());
end = Math.max(arr[i], end);
}
method(start, end);
System.out.println(ans);
}
static void method(int start, int end){
while(start<=end){
int total = 0;
int mid = (start + end) / 2;
for(int i=0;i<arr.length;i++){
if(arr[i] > mid){
// 떡이 가운데보다 길면
total += arr[i] - mid;
}
}
if(total < M){
// 떡 길이가 총 길이보다 작은 경우
end = mid - 1;
} else if(total >= M){
// 떡 길이가 총 길이보다 긴 경우
start = mid + 1;
ans = mid;
}
}
}
}동적계획법
점화식으로 표현하는 것
메모이제이션
기록해두는 것(동적계획법에서만 나오는 것은 아님)
완탐 모두 수행하지 않는 방법
- 메모이제이션: 기록해두고 마치 간 것처럼 하는 방법
- 가지치기: 중간 과정에서 불필요한 탐색을 가지 않는 것
현재의 것을 만들려면 이전의 것을 어떻게 써야 하는지를 고민해야 함.
바닥 공사
문제
가로의 길이가 N, 세로의 길이가 2인 직사각형 형태의 얇은 바닥이 있다.
이 얇은 바닥을 1x2의 덮개, 2x1의 덮개, 2x2의 덮개를 이용해 채우고자 한다.
이때 바닥을 채우는 모든 경우의 수를 구하는 프로그램을 작성하시오. (796,796으로 나눈 나머지를 출력)
풀이
i-1이라고 하면 남은 자리는 1x2로 하나 밖에 올 수 없다.
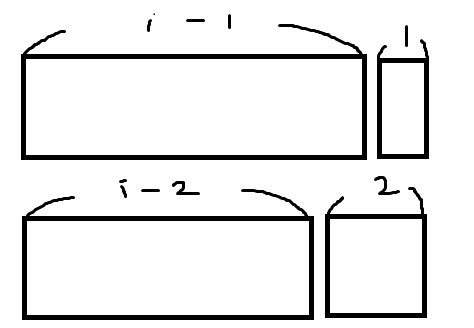
i-2라고 하면 뒤에 2x2 자리가 남게 되는데 여기에는 2x2블록 하나 / 1x2블록 2개 / 2x1블록 2개를 배치할 수 있다.
즉 3개가 올 수 있게 된다.
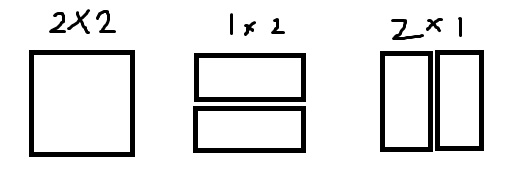
여기서 1x2 블록을 놓는 것은 i-1에서 계산하므로 점화식은 dp[i-1] + dp[i-2] * 2가 된다.
package _240628;
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class 바닥공사 {
public static void main(String[] args) throws Exception {
BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bufferedReader.readLine());
int dp[] = new int[N+1];
dp[1] = 1;
dp[2] = 3;
for(int i=3;i<=N;i++){
dp[i] = (dp[i-1] + dp[i-2] * 2) % 796796;
}
System.out.println(dp[N]);
}
}