1. Activation Function (활성 함수)

Activation Function (활성 함수): transfer function에서 전달받은 값을 non-linear하게 변화시켜주는 함수.

• 이를 통해 더욱 깊게 Neural Net을 쌓을 수 있게 된다.
• Linear하게 네트워크가 형성되면 a(a(ax+b)+b)+b 와 같이 될 것이고, back propagation시 vanishig problem이 발생할 수 있다.

종류(예시)

• 시그모이드 함수 (네트워크가 깊어짐에 따라 지금은 잘 안씀)

• tanh 함수: 지금은 잘 안 씀

• relu 함수: 음수값은 0, 양수값은 y=x 형태의 활성함수
  - 음수값의 입력시 학습 능력이 감소할 수 있음.

  • 보편적으로 쓰이는 활성함수

• leaky relu 함수:
  - relu의 음수 입력시 문제를 해결하기 위한 활성함수

  • 음수쪽은 0.001x와 같이 매우 작은 기울기 값을 갖는다.

• softmax 함수: 분류 네트워크에서 가장 마지막에 오는 셀

  2. Loss Function (손실 함수)

  Loss Function (손실 함수): gradient를 이용하여 오차를 비교하고 최소화하는 방향으로 이동시키는 방법.

• 평균 제곱 오차 $MSE = \frac{1}{n}\sum_{i=1}^n(y_i-\hat{y_i})^2$
  - Regression에서 많이 사용되는 함수

• 크로스 엔트로피 $CrossEntropy = -\sum_{i=1}^ny_i\text{log }\hat{y_i}$
  - 분류에서 one-hot encoding 했을 때만 사용할 수 있는 오차 계산법

  • softmax함수를 곱하여 만든 수식이다. (Maximum Likelihood Estimation)
  • $softmax(w^TX_i) = \hat{y_i}$인 것이고, one-hot encoding에 의해 $y_i$의 값들이 정의 되었으므로,
  • $\prod_isoftmax(w^TX_i)^{y_i} = \prod_i\hat{y}^{y_i}$가 된 것.
  • 이 함수의 최댓값을 구하는 문제이므로, -log를 취해주면 $CrossEntropy = -\sum_{i=1}^ny_i\text{log }\hat{y_i}$ 식이 나오는 것이다.

3. Feedforward, Backpropagation (순전파, 역전파)

• Feedforward: input layer에 들어온 data가 모든 hidden layers를 통과하여 output layer에 도달하는 과정.
• Backpropagation: output layer에서 반대로 hidden layer, input layer에까지 손실 비용이 전달되어 파라미터를 업데이트 하는 학습 과정.

4. 딥러닝의 문제점과 해결 방안

4-1. Over-fitting (과적합)

Over-ftting (과적합): Train data에서 loss 값은 작으나, Test data에서는 오차가 증가하는 경우

• Train data가 적을 때 발생
• 데이터를 과하게 학습할 때 발생

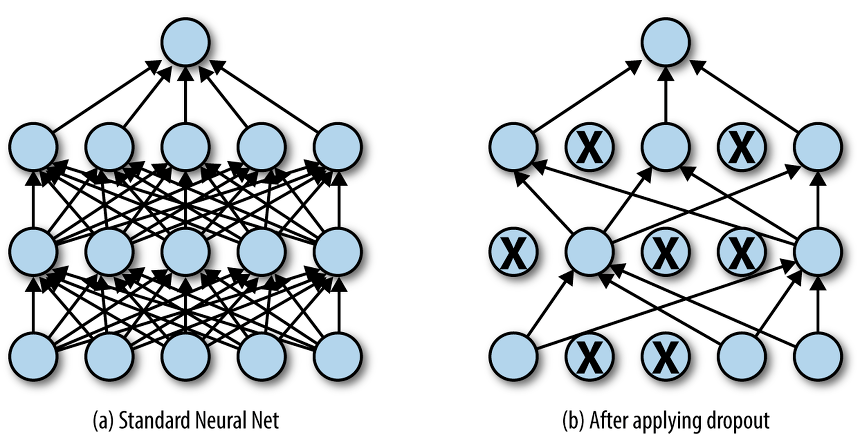
해결 방안: 드롭아웃 (dropout)

• 신경말 모델이 과적합되는 것을 피하기 위한 방법
• 학습 과정 중 임의로 일부 노드들을 학습에서 제외시킴.
  

4-2. Vanishing Gradient Problem (기울기 소멸 문제)

Vanishing Gradient Problem(기울기 소멸 문제): 기울기 (gradient)값이 소멸되어 input layer 까지 gradient 값이 전달되지 않는 것.

->이 때문에 오차를 더 줄이지 못하고 그 상태로 수렴하는 현상

• hidden layer이 많은 신경망에서 주로 발생

해결방안: sigmoid나 tanh 대신 relu Activation Function을 사용하면 해결할 수 있음.

4-3. 경사하강법에서 성능이 나빠지는 문제 발생

: 경사 하강법은 손실 함수의 비용이 최소가 되는 지점을 찾을 때까지 기울기가 낮은 쪽으로 계속 이동시키는 과정을 반복하는데, 이때 성능이 나빠지는 문제가 발생함.

-> 해결방안: SGD, MiniBatch GD

경사 하강법의 종류

• Batch Gradient Descent: total train dataset에 대해 가중치를 편미분하는 방법
  - 전체 데이터 셋에 대한 에러를 구한 뒤 기울기를 단 한번만 계산하여 모델의 파라미터 업데이트를 진행하는 것이다.
  • 전체 학습 데이터에 대해 한번의 업데이트가 이뤄지기 때문에 전체적인 연산 횟수가 적다.
  • 전체 데이터에 대해 gradient를 계산하여 진행하기 때문에, 최적으로의 수렴이 안정적으로 진행된다.
  • 모든 학습데이터를 사용하기 때문에 오래걸린다.
  • Local optimal에 빠지면 빠져나오기 힘들다.
• SGD (확률적 경사 하강법): BGD의 오래 걸리는 단점을 개선한 방법이다. 임의로 선택한 데이터에 대해 기울기를 계산하는 방법으로 적은 데이터를 사용하므로 빠른 계산이 가능.
• mini-Batch gradient descent (미니 배치 경사 하강법): 전체 데이터셋을 미니 배치 여러개로 나누고, 미니 배치 한 개마다 기울기를 구한 후 그것의 평균 기울기를 이용하여 모델을 업데이트.
  --> SGD보다 안정적이고, BGD보다 빠르다.
  --> 실제로 가장 많이 사용하는 방법.
  --> 변경 폭이 SGD에 비해 안정적이면서 속도도 빠르다.

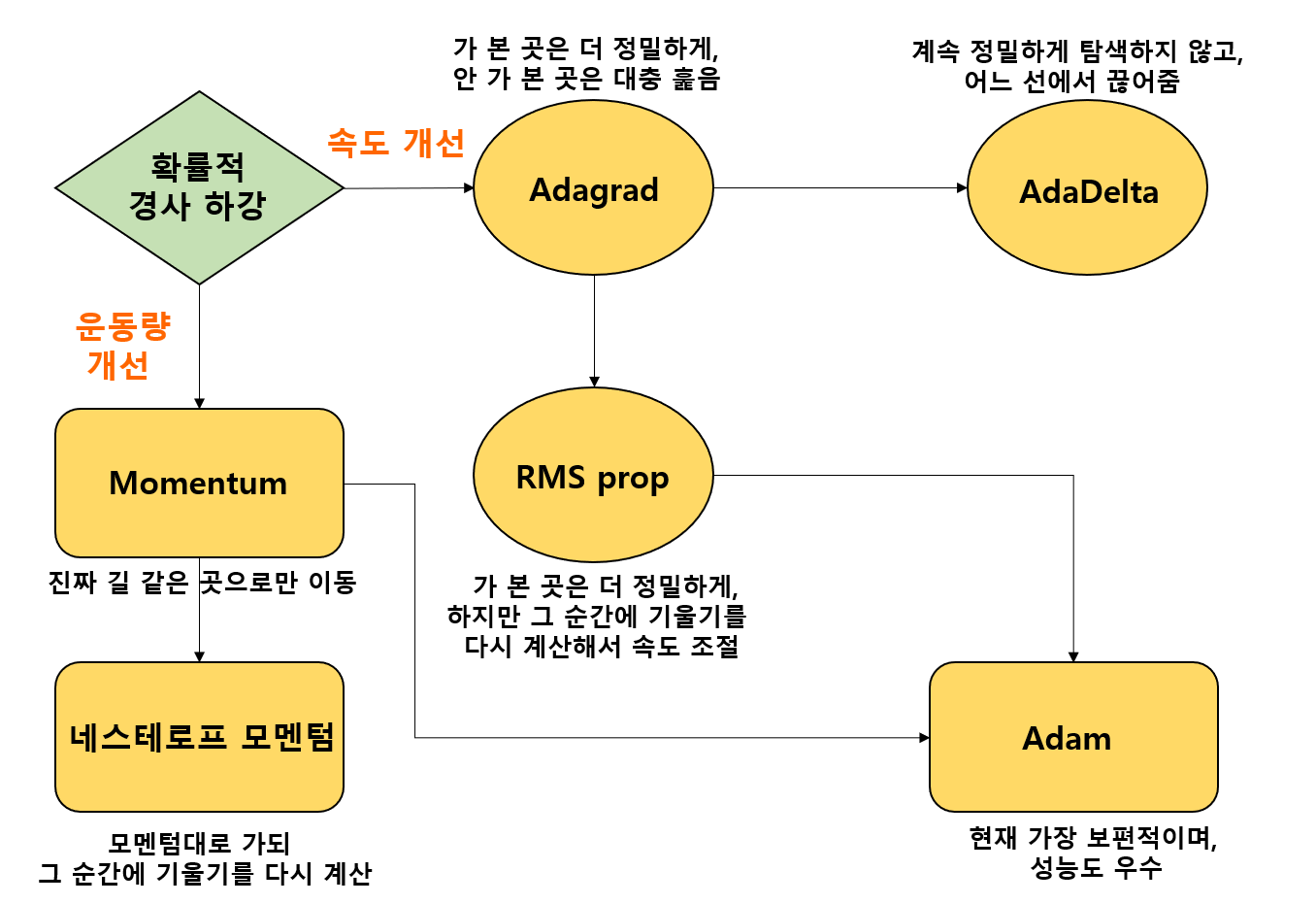
5. Optimizer

optimizer (옵티마이저): gradient descent의 방법으로 파라미터를 학습할 때, 파라미터 변경 폭이 불안정한 문제를 해결하기 위해 학습 속도와 운동량을 조정하는 것.

속도를 조정하는 방법 (learning rate를 조정하는 방법)

• 아다그라드 (Adagrad): 파라미터의 업데이트 횟수에 따라 learning rate (이하 lr)를 조정
  - 많이 변화하지 않는 변수들의 lr는 크게 하고, 많이 변화하는 변수들의 lr는 작게함.
  • 즉 많이 변화한 파라미터는 최적 값에 근접 했을 것이라는 가정하게 작은 크기로 이동하면서 세밀하게 값을 조정
  • 반대로 적게 변화한 파라미터들은 lr를 크게 하여 빠르게 오차 값을 줄이고자 하는 방법

    

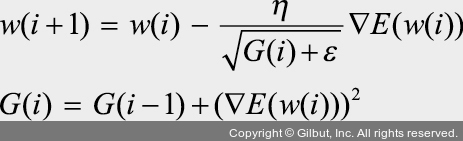
    • 파라미터마다 다른 lr을 부여하기 위해 G함수를 추가함.
    • 기울기가 크면 (즉 많이 변화한 파라미터는) G 값이 커지기 때문에 lr은 작아지게 됨.

• 아다델타 (Adadelta): 아다그라드에서 G값이 커짐에 따라 학습이 멈추는 문제를 해결하기 위해 등장한 방법
  - lr에 대한 하이퍼파라미터가 필요 없음.
  
• RMSProp: 아다그라드의 G(i)값이 무한히 커지는 것을 방지하고자 제안된 방법

운동량을 조정하는 방법

• 모멘텀 (Momentum): 가중치를 수정하기 전에 이전 수정 방향을 참고하여 같은 방향으로 일정한 비율만 수정하는 방법.
  - $w(i+1) = w(i) - v(i)$
  - $v(i) = \gamma v(i-1) + \eta\bigtriangledown L(w(i))$
  • 이때 단순히 손실함수의 편미분 값만 빼는게 아닌, 이전 운동량 v(i-1)고려하여 같이 빼준다.
• 네스로프 모멘텀: 모멘텀 값이 적용된 지점에서 기울기 값을 계산.
  - $w(i+1) = w(i) - v(i)$
  - $v(i) = \gamma v(i-1) + \eta\bigtriangledown L(w(i)-\gamma v(i-1))$
  • 이때 $L(w(w)-\gamma v(i-1))$ 텀이 절반 정도 이동한 다음에 다시 기울기를 계산한 텀이다.
  • 이로써 모멘텀 방법의 이점인 빠른 이동 속도는 그대로 가져가면서 멈추어야 할 적절한 시점에서 제동을 거는 데 훨씬 용이함.

속도와 운동량에 대한 혼용 방법

• 아담 (Adam):모멘텀과 RMSProp의 장점을 결합한 경사하강법.
  - 파라미터마다 다른 학습률을 추가하면서, 이 학습률을 모멘텀의 v(i) 텀에 응용
  • $w(i+1) = w(i) - v(i)$
  • $G(i) = \gamma_2 G(i-1) + (1-\gamma_2)(\bigtriangledown L(w(i)))^2$
  • $v(i) = \gamma_1 v(i-1) + \eta\bigtriangledown L(w(i))$
    ->현재 가장 보편적이며, 성능도 우수하다.