🔗 Paper Link

Summary ❕

💡 기존의 복잡한 RNN, CNN 모델 기반의 sequence data 처리 방식 및 한계
(데이터가 길어짐에 따라 발생하는 손실, 우상향 연산량) 해결 방안의 제시 = “Transformer”

 

Review 🗒️

0. Abstract

Previous : Complex RNN, CNN을 이용한 Sequence transduction

“Transformer” ; Simple Network

• 오직 attention 기법을 이용한 구현
• More parallelizable ; 병렬 연산 가능
• Significantly less training time

---

1. Introduction

Previous : Recurrent net (LSTM, GRU) - hidden state $h, h_{t-1}$ 을 이용

• Precludes parallelization
  • 병렬적 연산 불가능, 연속 처리 필요
• 긴 순차 데이터 처리에 한계
  - RNN 모델의 Sequence data 처리 시 고질적 문제

“Transformer”

• Global dependencies between input & output
• More parallelization
• Less training time

---

2. Background

To reduce sequential computation → requires operation to relate signals :
Previous : Extended Nerual GPU ByteNet, ConvS2S

• Linear, log growing operation

“Transformer” :

• constant num operation
  • 상수 연산

• Self-attention (a.k.a intra-attention)
  • Relate different positions of a single sequence → compute representation

---

3. Model Architecture

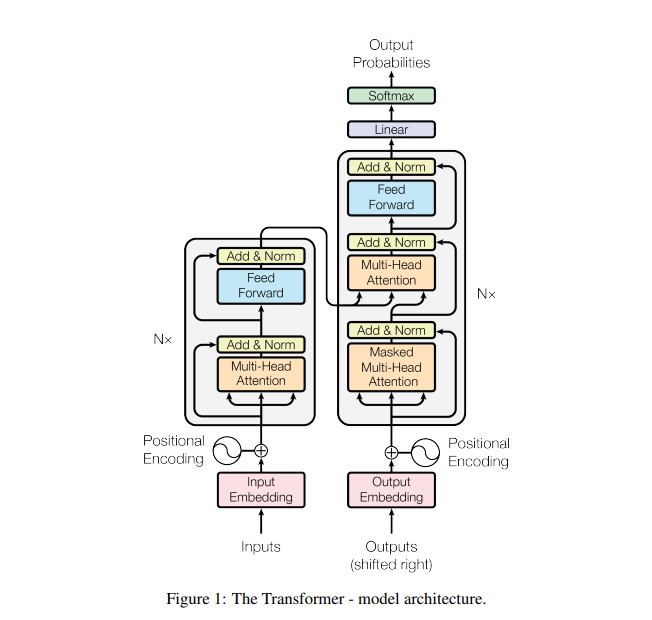
3.1 [Figure 1] The Transformer - model architecture

하나의 N layer에 대한 구조

• Input seq $x$ → encoder → $z$
  • $z$ ; sequence of continuous representations
    • 연속된 개념 집합으로 mapping
• $z$ (encoder output) → decoder → Output seq $y$

• 매 스텝마다 모델은 auto-regressive
  • 이전에 생성된 symbol들을 다음 출력 생성 시 추가 입력으로 받음
• Stack of FC layers for encoder, decoder

 

Encoder, Decoder 내부

Encoder

• N = 6 identical layers
  • 각 레이어마다 2개의 sub-layer [Fig.1의 좌측부] & 정규화 레이어
    • Multi-head Attention mechanism
    • FC Feed Forward network
  • Input 차원 = Ouput 차원 = $d_{model} = 512$
    

Decoder

• N = 6 identical layers
  • encoder와 동일한 구조의 2개의 sub-layer [Fig.1의 우측부]
    • ‘Masked’ Multi-head Attention
      • position $i$ 에 대한 예측이 $i-1$까지의 출력을 기반으로 이루어지도록 함
      • 자기 자신과 그 이전의 단어들만을 참고한 Self-attention
  • Third sub-layer
    • Multi-head attention
      • encoder output을 받아 연산 수행

 

3.2 [Figure 2] Scaled Dot-Product (left). Multi-Head Attention : parallel (right)

✒️ What is Attention?

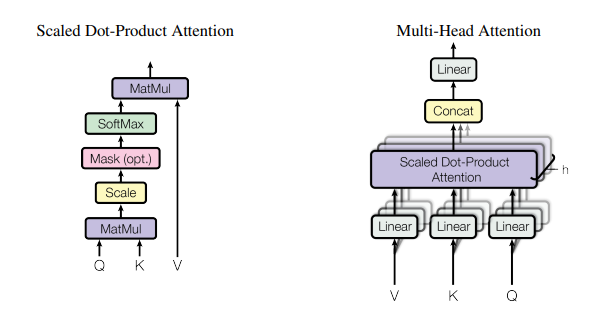
• Attention function
  • Mapping (query, set of key values) with output, using weighted sum
    • All vectors (Q, K, V)

 

• Scaled Dot-Product Attention [Fig.2의 좌측]
  • Input : Queries, Keys of dimension $d_k$, Values of dimention $d_v$
  • Computaion
    • MatMul : dot product
    • Scale : $1 / sqrt(d_k)$

 

• Attention 연산의 종류
  • Dot-product + Scale (해당 논문에서 이용하는)
    • Identical to this algorithm
    • Faster & space-efficient
    • In large values of $d_k$ ; push softmax → small gradient problem
      • Reason why we scale
  • Additive attention
    
  • Use feed forward net & single hidden layer
    
  • Outperforms in small values of $d_k$
    

 

• Concatenation
  • Single-head와 같은 크기의 output 도출
    • Input 문장 행렬$(seq\_len, d_{model})$과 동일 크기
  • h개의 차원으로 나뉘어 연산, but 전체 연산량은 single과 유사
    

 

• Multi-Head Attention [Fig.2의 좌측]
  : Linearly project Q, K, V ⇒ h times
  • Attention function : h 겹의 layer에 대한 동시 연산 수행
  • $d_q, d_k, d_v$ 는 h개의 차원으로 나뉘어 연산 → 이후 concat을 이용한 결합

💡 모델은 different position의 개념 부분집합(representation subspaces)에 공통적 관여 가능

• single attention head ; averaging inhibits this

 

3.3 Position-wise Feed-Forward Networks

• Used in encoder and decoder, Fully connected
  • ReLU를 이용한 2개의 선형 변환 : $W_1, W_2$

• FFN 연산 개념
  $x$는 Multi-head attention 출력 결과물
  

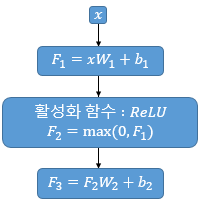
• Input $x$와, $FFN(x)$의 차원은 동일하게 유지

• 이때 해당 모델에서, $d_{model} = 512,\ d_{ff} = 2048$

  $x$	$(seq\_len, d_{model})$
  $W_1$	$(d_{model}, d_{ff})$
  $W_2$	$(d_{ff}, d_{model})$
  $FFN$	$(seq\_len, d_{model})$

 

3.4 Embeddings and Soft- 3.5 Positional Encoding

• 해당 모델에서는 Recurrence & Convolution을 배제
• 입력 토큰의 순서 정보를 전달하기 위해 이용

  • PE는 $d_{model}$ 차원 (연산 가능하게 하기 위함)

  • where $pos$ : position, $i$ : dimension

    $PE_{pos, 2i} = sin(pos/10000^{2i/d_{model}}) \\ PE_{pos, 2i+1} = cos(pos/10000^{2i/d_{model}})$

---

4. Why Self-Attention

[Table 1] 복잡도 비교

• Recurrent, Convolution에 비해 적은 연산량
• Advantages in
  • Total computation and complexity per layer
  • Amount of computation that can be parallelized
  • Path length between long-range dependencies in the network