소수란?
1과 자기 자신 외의 약수를 가지지 않는 1보다 큰 자연수
소수 구하기 기본 알고리즘
시간 복잡도 O(n)의 알고리즘
bool primeNumCheck_N(int n) {
if (n == 1)
return false;
for (int i = 2; i < n; i++) {
if (n % i == 0)
return false;
}
return true;
}시간 복잡도 O(sqrt(n))의 알고리즘
N의 약수의 약수(?)는 무조건 sqrt(N) 범위 안에 존재한다.
숫자 12를 예로 들자면,
sqrt(12) = 3.xxx
12의 약수는 1, 2, 3, 4, 6, 12이다.
소수가 아닌 1과 12를 제외하고 남은 수들의 조합을 살펴볼 때,
2x6, 3x4 / 4x3, 6x2 와 같이 12를 만들 수 있는 조합이다.
( sqrt(12) = 3.xxx )
결국 어떤 수가 소수인지 소수가 아닌지 모듈러 나눗셈을 통해 확인하려면 2~sqrt(n) 범위에서만 확인하면 된다.
bool primeNumCheck_sqrtN(int n) {
if (n == 1)
return false;
for (int i = 2; i * i <= n; i++) {
if (n % i == 0)
return false;
}
return true;
}예제 문제: 소수 구하기_백준
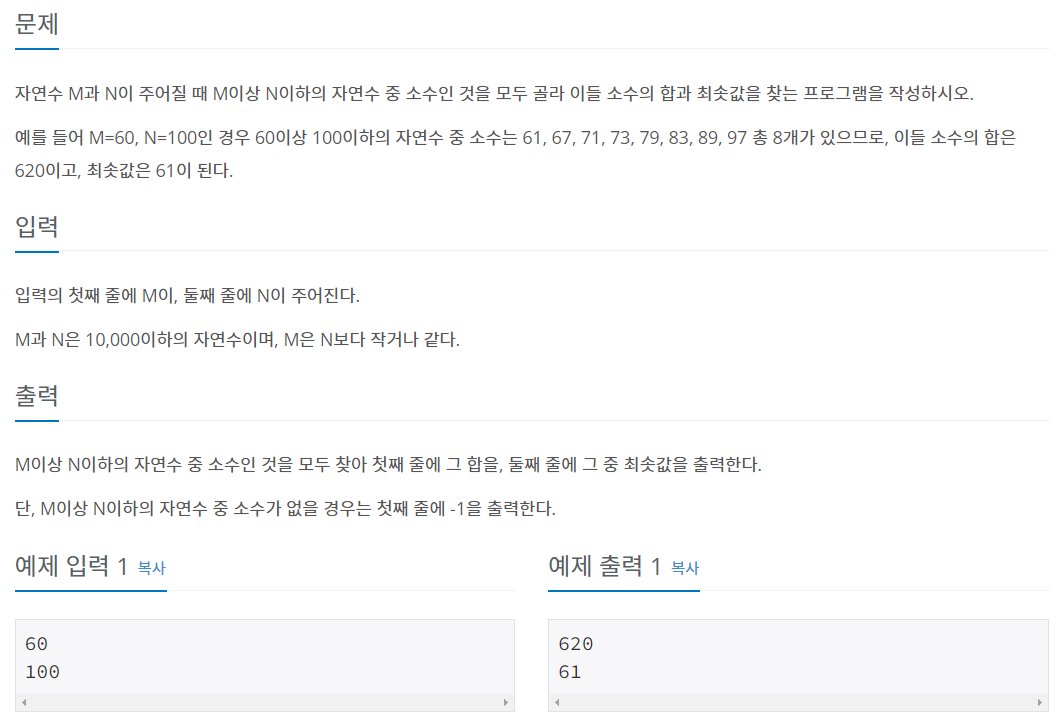
입력 조건에 따르면 O(n)의 시간 복잡도를 가진 소수 판별 알고리즘이나 O(sqrt(n))의 그것이나 상관없이 모두 통고한다.
#include <bits/stdc++.h>
using namespace std;
bool primeNumCheck1(int n){ // O(n)
if(n==1)
return false;
for(int i=2; i<n; i++){
if(n%i == 0)
return false;
}
return true;
}
bool primeNumCheck2(int n){ // O(sqrt(n))
if(n==1)
return false;
for(int i=2; i*i <= n; i++){
if(n%i == 0)
return false;
}
return true;
}
pair<int, long long> solution(int m, int n){
pair<int, int> result;
int min_prime = -1;
long long total = 0;
bool first = true;
// 소수 최저와 합 구하기
for(int i=m; i<=n; i++){ // O(N)
if(primeNumCheck2(i)){ // 소수 발견
if(first){
min_prime = i;
first = false;
}
total += i;
}
}
result = {min_prime, total};
return result;
}
int main(){
int m, n;
cin >> m >> n;
pair<int, long long> result = solution(m, n);
if(result.first != -1){
cout << result.second << '\n';
}
cout << result.first << '\n';
}예제 문제: 소수 구하기_백준
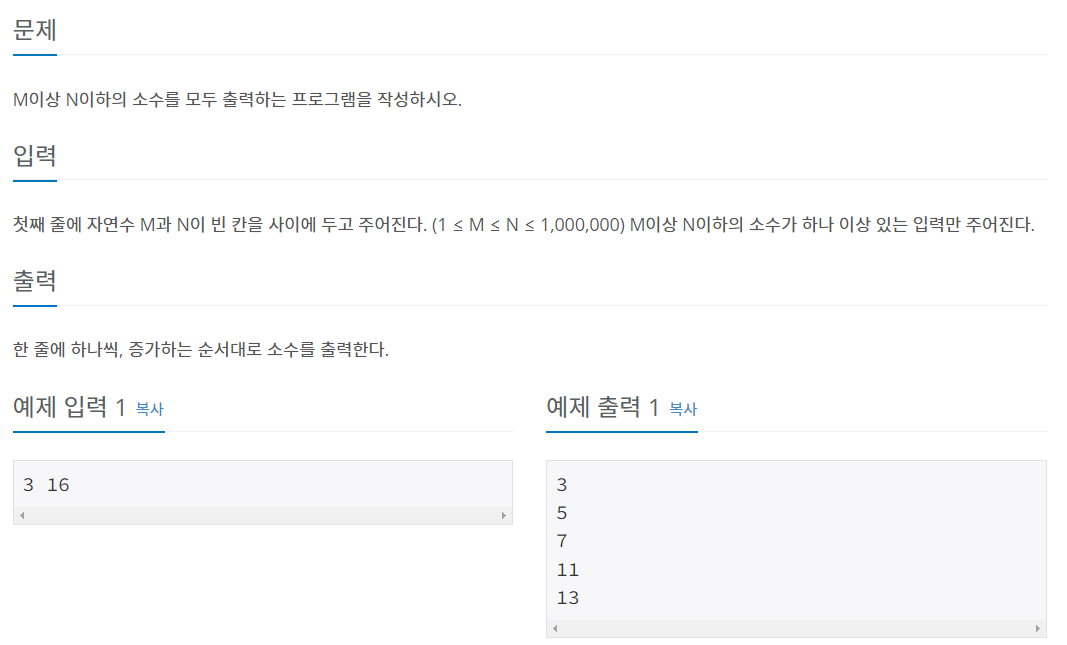
입력 조건에 따라 O(n)의 시간 복잡도를 가지는 소수 판별 알고리즘으론 해결할 수 없다. 시간 초과가 발생한다.
따라서 O(sqrt(n))의 시간 복잡도를 가지는 소수 판별 알고리즘으로 해결해야 한다.
#include <bits/stdc++.h>
using namespace std;
// O(sqrt(n))
bool primeNumCheck(int n){
if(n==1)
return false;
for(int i=2; i*i <= n; i++){
if(n%i == 0)
return false;
}
return true;
}
vector<int> solution(int m, int n){
vector<int> primes;
// 소수 최저와 합 구하기
for(int i=m; i<=n; i++){ // O(N)
if(primeNumCheck(i)){ // 소수 발견 // O(sqrt(N)) => O(N*sqrt(N))
primes.push_back(i);
//cout << "i'm a prime: " << i << '\n';
}
}
return primes;
}
int main(){
int m, n;
cin >> m >> n;
vector<int> result = solution(m, n);
for(int i=0; i < result.size(); i++){
cout << result[i] << '\n';
}
}cf) 에라토스테네스의 체
에라토스테네스의 체
소수(x)의 배수는 약수로 무조건 x를 포함하게 된다.
따라서 절대 소수의 배수는 소수가 될 수 없다. 이를 이용한 것이 에라토스테네스의 체이다.
누구나 알고있는 가장 작은 소수인 2부터 시작해서, 2의 배수를 다 지웠으면, 지워지지 않은 수 중에서 다음 값인 3의 배수를 지워나가고 이를 계속해서 반복해 나가면 소수만 남게된다.
마치 체에 걸러서 남는 것들만 뽑아내는 방식이라고 생각하면 된다.
(source: https://jm-park.github.io/algorithm/2018/08/06/Prime-Number(%EC%86%8C%EC%88%98)-%ED%8C%90%EB%B3%84%EB%B2%95-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98.html)
위키백과의 움짤을 보면 바로 이해 가능
reference: https://ko.wikipedia.org/wiki/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98_%EC%B2%B4
예제 문제: 에라토스테네스의 체_백준
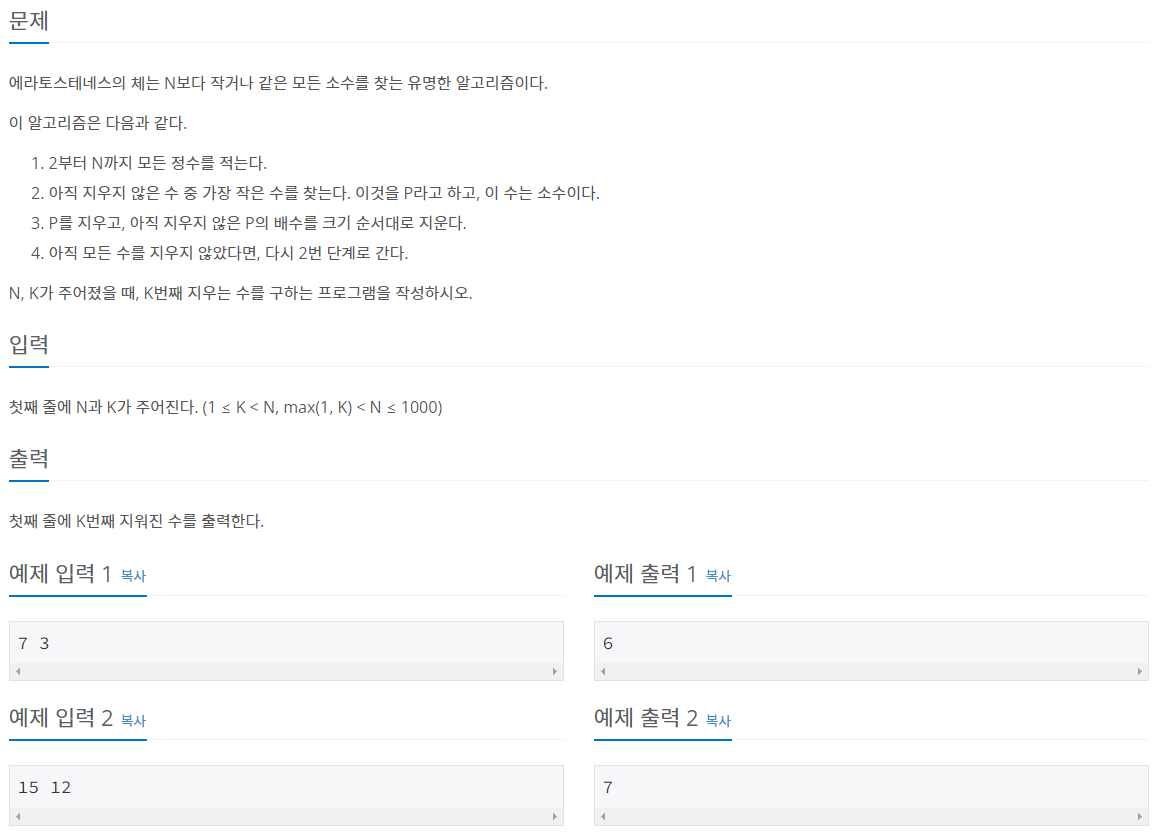
#include <bits/stdc++.h>
using namespace std;
/*
2 4 6 8 10 12 14
3 9 15
5
7
*/
int solution(int n, int k){
vector<int> arr;
set<int> primes;
int cnt = 0;
for(int i=2; i<=n; i++){
int now_num = i;
for(int j=1; now_num*j <= n; j++){
if(primes.find(now_num*j) == primes.end()){
primes.insert(now_num*j);
arr.push_back(now_num*j);
cnt++;
if(cnt == k){
// set 순회
return arr[arr.size()-1];
}
}
}
}
return -1;
}
int main(){
int n, k;
cin >> n >> k;
int result = solution(n, k);
cout << result << '\n';
}