가중치 초기화

참고 자료

윤성진, [Do it! 딥러닝 교과서], 이지스퍼블리싱(2021), 162p ~ 171p

가중치 초기화란?

• 손실 함수에서 출발 위치를 결정하는 방법

상수 초기화

• 사전 정보가 없다고 가정했을 때 임의의 상수로 초기화하는 방법을 생각해볼 수 있다.

0으로 초기화한다면?

아래와 같은 산식에 따르면 가중치가 0인 경우 가중 합산 결과는 항상 0이되고 가중 합산 결과인 0을 입력받아 늘 같은 값을 출력하게 된다.

또한,

역전파 과정에서 $\frac{\delta{z}}{\delta x}$ 는 $w$이므로 항상 0이 되고, 학습이 진행되지 않는다.

0이 아닌 상수로 초기화한다면?

가중치를 모두 같은 상수로 초기화하면 신경망에 대칭성이 생겨서 같은 계층의 모든 뉴런이 똑가이 작동하므로, 여러 뉴런을 사용하는 의미가 없어지고, 하나의 뉴런만 있는 것과 같게 된다.

분포를 따르는 난수로 초기화

Xavier 초기화(Xavier initialization) 또는 He 초기화(He initialization)와 같은 가중치 초기화 방법을 사용

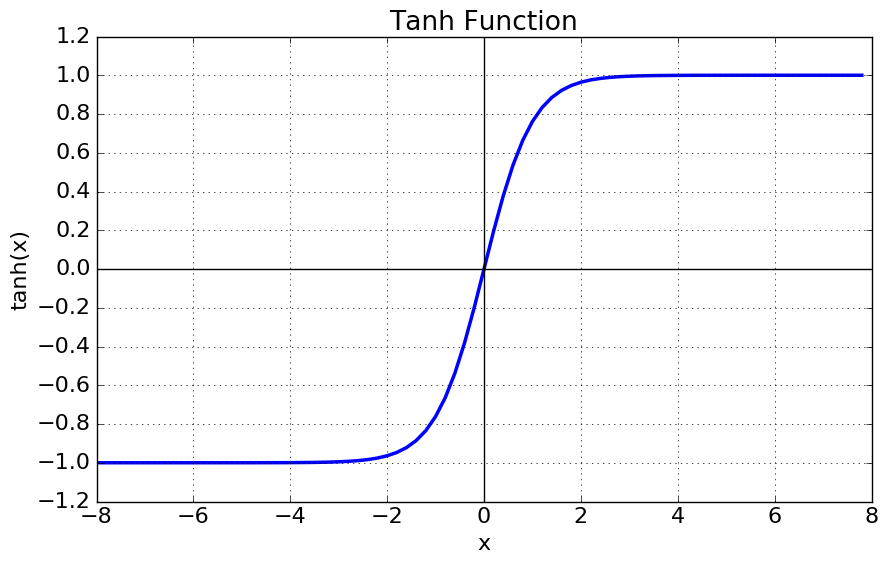
Xavier initialization

각 층의 입력과 출력 뉴런 수에 기반하여 가중치를 초기화, sigmoid나 tanh 같이 입력값이 중앙(0부근)에서 직선에 가까워 선형함수로 가정할 수 있는 활성함수에 효과적이다.

초기화 방식 유도

1. 활성함수를 선형 함수로 가정

• 입력 데이터가 0 근처의 작은 값으로 되어 있다고 하자
• 이 입력 데이터는 활성 함수의 가운데 부분을 지난다.
• 활성 함수의 가운데 부분은 직선에 가깝기 때문에 선형 함수로 가정

2. 입력데이터와 가중치에 대한 가정

• 입력 데이터와 가중치는 서로 독립
• 입력 데이터와 가중치는 각각 iid 만족, 평균이 0인 분포를 따름
  

뉴련의 출력 y는 가중합산 z와 같다.

여기서 입력과 출력의 분산을 같게 만들기 위해 $Var(y)=Var(x)$라고 한다면
$Var(w)=\frac{1}{n}$이 된다.

He initialization

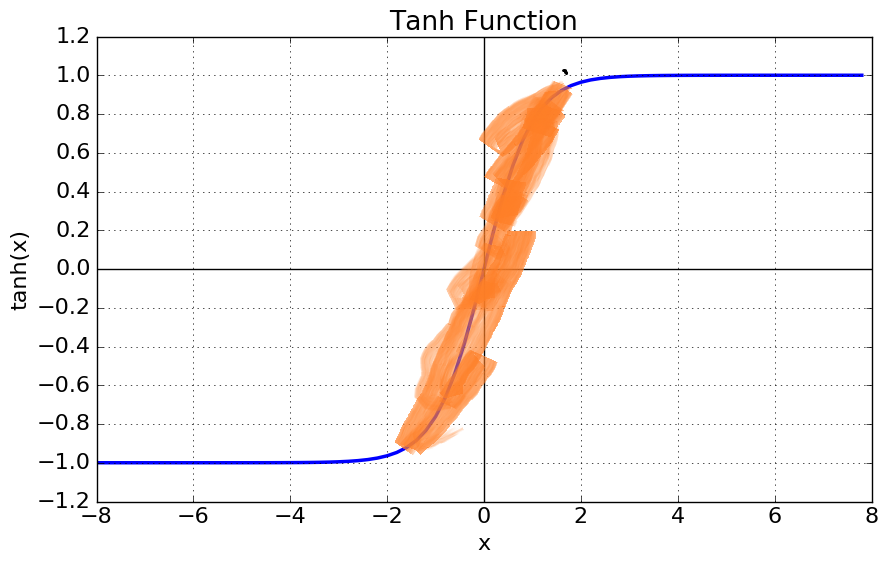
활성함수가 ReLU일 때 Xavier initialization을 사용하면 데이터의 크기가 점점 작아진다.

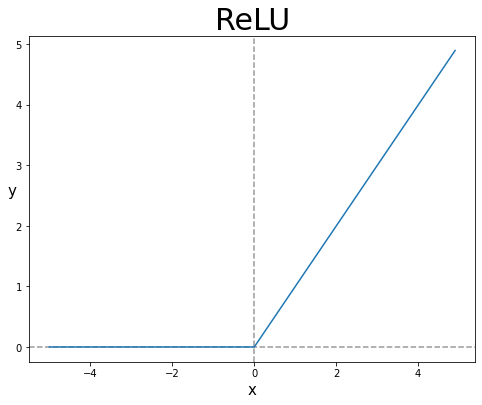
이는 simoid 계열의 가정 중 중앙(0부근) 에서 선형성을 띤다고 가정하였는데 ReLU의 경우에는 가정이 유효하지 않고, 0보다 작은 값에 대해서 입력 데이터가 0으로 변하므로 50% 가량의 데이터가 0이 된다면, 분산이 절반으로 줄어들게 된다.

따라서 위와 같은 문제를 해결하기 위해, 가중치의 분산을 2배인 2/n으로 사용한다.