정규화(Regularization)

Jinho Jang·2023년 6월 30일
DLbookpython
0

참고 자료

윤성진, [Do it! 딥러닝 교과서], 이지스퍼블리싱(2021), 172p ~ 184p

정규화란

  • 최적화 과정에서 최적해를 잘 찾도록 정보를 추가하는 기법
  • 최적화 과정에서 성능을 개선할 수 있는 포괄적인 기법들을 포함한다.

1. 배치 정규화(Batch Normalization), 계층 정규화(Layer Normalization)

1.1 내부 공변량 변화

  • 신경망 학습에서 계층을 지날 때마다 데이터 분포가 보이지 않는 요인에 의해서 조금씩 왜곡된다.
  • 이러한 현상을 내부 공변량 변화(Internal covariate shift)라고 한다.

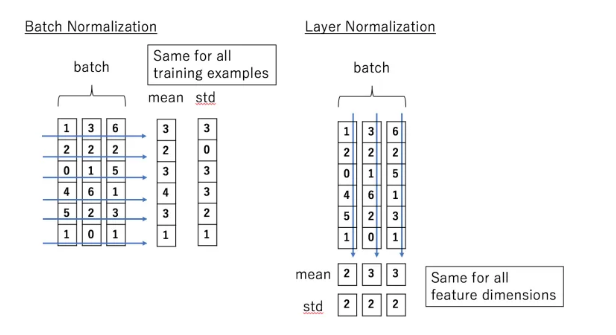
1.2 배치 정규화(Batch Normalization)

  • 배치 정규화는 데이터가 계층을 지날 때마다 정규화해서 내부 공변량 변화를 없애는 방법이다.
  • 미니 배치 내의 평균과 분산을 사용하여 입력 데이터를 평균 0, 분산 1로 정규화한다.
  • 배치 정규화 알고리즘
  • 학습 단계에서는 미니배치 단위의 평균과 분산으로 정규화를 수행하고, 테스트 단계에서는 전체 데이터의 평균과 분산으로 정규화한다.
  • 미니 배치로 구한 평균 μB\mu_B과 분산 σB2\sigma^2_B에 대해 다음과 같이 이동 평균을 구해서 전체 데이터의 평균과 분산을 계산한다.
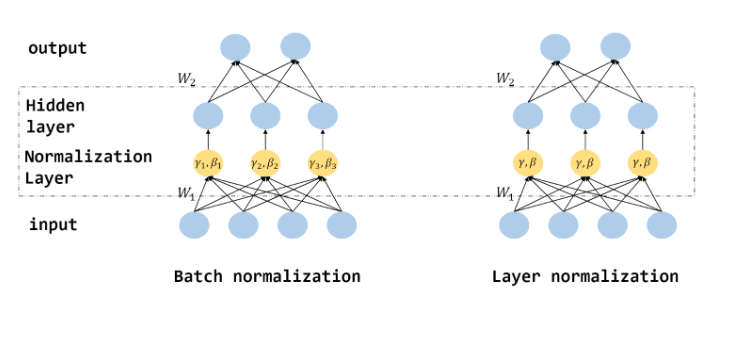
E[x]←EB[μB]Var[x]←mm−1EB[σB2]E[x]\leftarrow E_B[\mu_B]\\ Var[x]\leftarrow \frac{m}{m-1}E_B[\sigma^2_B]

1.3 배치 정규화 수행 위치

배치 정규화는 주로 활성화 함수 이전에 적용하는 것이 일반적으로 더 좋은 결과를 얻을 수 있다.
활성 함수 이전에 사용한다면 다음과 같은 이점을 얻을 수가 있다.

  • 그래디언트 전파 개선

    • 배치 정규화는 입력 데이터를 정규화하여 평균과 분산을 조정하는 과정을 포함한다.
    • 즉, 각 미니 배치의 그래디언트가 적절하게 조절되어 그래디언트의 전파가 원활하게 이루어지면 모델 학습의 안정성과 수렴 속도를 높인다.

  • 스케일과 시프트

    • 배치 정규화는 정규화된 입력 데이터에 스케일과 시프트를 적용할 수 있는 매개변수인 gamma와 beta를 사용한다.
    • 이로 인해 모델이 데이터의 선형 변환을 수행하고 적절한 비선형성을 학습할 수 있다.

  • 입력 분포 안정화

    • 배치 정규화는 입력 데이터의 평균과 분산을 조정하여 입력 분포를 안정화시킨다.
    • 활성화 함수에 들어가는 입력의 범위를 일정하게 유지함으로써, 활성화 함수가 좀 더 일반적인 범위에서 작동하게 한다.
    • 모델의 표현 능력을 향상시키고, dead neurons 문제를 완화할 수 있다.

다만 책에서는 활성 함수를 실행한 뒤에 배치 정규화를 수행했을 때 더 나은 성능을 보이는 경우도 있다고 하니, 모델의 성능을 세밀하게 개선하기 위해서는 활성 함수 이후에 적용한 케이스도 검증해 볼 필요가 있다고 언급하였다.

1.4 계층 정규화(Layer normalizaiton)

기존의 배치 정규화에는 다음과 같은 문제점이 있다.

  • 배치 정규화의 효과는 batch size에 따라 달라진다.
  • 데이터가 큰 경우 Mini Batch도 크기 때문
  • RNN처럼 Instance 별 길이가 다른 경우 사용할 수 없다.

계층 정규화(Layer normalization)은 batch에 있는 모든 feature의 평균과 분산을 구한다. 즉, 각 hidden node의 feature별 평균과 분산이 아닌 hidden layer 전체의 평균과 분산으로 normalization한다.

1.5 계층 정규화 수행 위치

배치 정규화와 다르게 계층 정규화는 활성화 함수 이후에 적용하는 것이 효과적이다.

  • 활성화 함수 이전에 Layer Normalization을 수행하면, 활성화 함수의 입력 범위가 달라지기 때문에 활성화 함수의 성질이 변할 수 있다. 활성화 함수 이후에 Layer Normalization을 수행하면, 활성화 함수의 입력 분포가 정규화되어 모델의 안정성을 유지하는데 도움이 된다.

  • 활성화 함수 이후에 Layer Normalization을 수행하면, 활성화 함수가 생성한 중요한 정보가 손실되지 않도록 보존된다. 활성화 함수는 입력 데이터의 비선형 변환을 수행하여 모델의 표현력을 향상시키는 역할을 하는데, Layer Normalization은 이러한 활성화 함수의 출력을 정규화하면서도 중요한 정보를 보존할 수 있도록 도와준다.

  • 정규화된 활성화 값을 기반으로 gradient가 전파되면, gradient의 크기가 일정하게 유지되어 학습 과정을 안정화시킨다.

2. 가중치 감소(Weight Decay)

최적화할 때는 다루는 숫자의 크기(sclae)가 작을 수록 오차의 변동성이 낮아지므로 파라미터 공간이 원점 근처에 있을 때 정확한 해를 빠르게 찾을 수 있다. 따라서, wTx+b=0w^Tx+b=0이란 식을 표현할 때 가중치와 편향이 작은 것이 좋다.
=> 가중치 감소는 학습 과정에서 작은 크기의 가중치를 찾게 만드는 정규화 기법이다.

2.1 가중치 감소 적용 방식

가중치 감소는 손실 함수에 정규화 항을 더하면, 최적화 과정에서 원래의 손실 함수와 함께 정규화 항도 같이 최소화 되므로 크기가 작은 가중치 해를 구할 수 있다.

J~(w)=J(w)+λR(w)\widetilde{J}(w) =J(w)+\lambda R(w)

정규화 항 R(w)R(w)은 가중치의 크기를 나타내는 norm으로 정의한다.

2.2 L1 정규화(L1 Regularization)

L1 regularization은 가중치의 절댓값에 대한 페널티를 손실 함수에 추가하여 가중치의 크기를 제한한다.

가중치 감소를 통해 희소성을 부여하는 특징이 있다.
최적해가 특정 차원의 축 위에 있을 가능성이 높기 때문인데, 이 경우 최적해가 존재하는 축을 제외한 나머지 축의 좌푯값이 0이 되므로 좌표의 대부분 값이 0으로 채워진 희소한 해를 가진다.
=> 유효 파라미터 수가 줄어들고, 작은 모델이 되어 성능이 빨라진다. 이러한 과정을 feature selection 과정으로 보기도 한다.

L1RegularizationJ~(w)=J(w)+λ∥w∥L1 Regularization \\ \widetilde{J}(w) =J(w)+\lambda \parallel w\parallel

2.3 L2 정규화(L2 Regularization)

L2 norm을 사용한 L2 regularization이 가중치 감소를 구현하는 방법으로 주로 사용된다. L2 regularization은 가중치의 제곱값에 대한 페널티를 손실 함수에 추가하여 가중치의 크기를 제한한다.

L2RegularizationJ~(w)=J(w)+λ∥w∥2L2 Regularization \\ \widetilde{J}(w) =J(w)+\lambda \parallel w\parallel^2
profile
Jinho Jang
이전 포스트

가중치 초기화

다음 포스트

이외 정규화 효과를 볼 수 있는 기법

0개의 댓글