Grandmaster-Level Chess Without Search (2024)

A paper by Google Deepmind.

Abstract

The recent breakthrough successes in machine learning are mainly attributed to scale: namely large- scale attention-based architectures and datasets of unprecedented scale. This paper investigates the impact of training at scale for chess. Unlike traditional chess engines that rely on complex heuristics, explicit search, or a combination of both, we train a 270M parameter transformer model with supervised learning on a dataset of 10 million chess games. We annotate each board in the dataset with action-values provided by the powerful Stockfish 16 engine, leading to roughly 15 billion data points. Our largest model reaches a Lichess blitz Elo of 2895 against humans, and successfully solves a series of challenging chess puzzles, without any domain-specific tweaks or explicit search algorithms. We also show that our model outperforms AlphaZero’s policy and value networks (without MCTS) and GPT-3.5-turbo-instruct. A systematic investigation of model and dataset size shows that strong chess performance only arises at sufficient scale. To validate our results, we perform an extensive series of ablations of design choices and hyperparameters.

1. Introduction

Existing Chess Engines

IBM's Deep Blue

• Defeated the world chess champion Garry Kasparov in 1997
• Expert system (chess knowledge database and heuristics + a strong tree search algorithm - alpha beta pruning)

Stockfish 16

• followed similar recipe
• world's strongest engine

AlphaZero

• exception => (search and self-taught heuristics w/o human chess knowledge)

Transformer and derived models

• (self-)supervised learning on expert data with attention-based architectures applied at scale
• resulted LLMs with impressive and unexpected cognitive abilities
• Unclear whether the same techinque would work in a domain like chess, where successful policies typically rely on sophisticated algorithmic reasoning(search, dynamic programming) and complex heuristics

Is it possible to use supervised learning to obtain a chess policy that gener- alizes well and thus leads to strong play without explicit search?

Contributions of the paper

• Apply general supervised training at scale to chess

Steps

• Supervised training to learn to predict action-values (win percentages) for chess boards.
• Uses Stockfish 16 as oracle to get a large corpus of "ground-truth" action-values
• Leads to strong, grandmaster-level chess policy

Therefore, our work shows that it is possible to distill a good approximation of Stockfish 16 into a feed-forward neural network via standard super- vised learning at sufficient scale—akin to the quote famously attributed to José Raúl Capablanca, world chess champion from 1921 to 1927: “I see only one move ahead, but it is always the correct one.”

Main Contributions

• Distill an approximation of Stockfish 16 into a neural predictor
• construct a policy from our neural predictor and show that it plays chess at grandmaster level (Lichess blitz Elo 2895) against humans
• ablations of the model size and data set size, showing that robust generalization and strong chess play only arise at sufficient scale

2. Methods

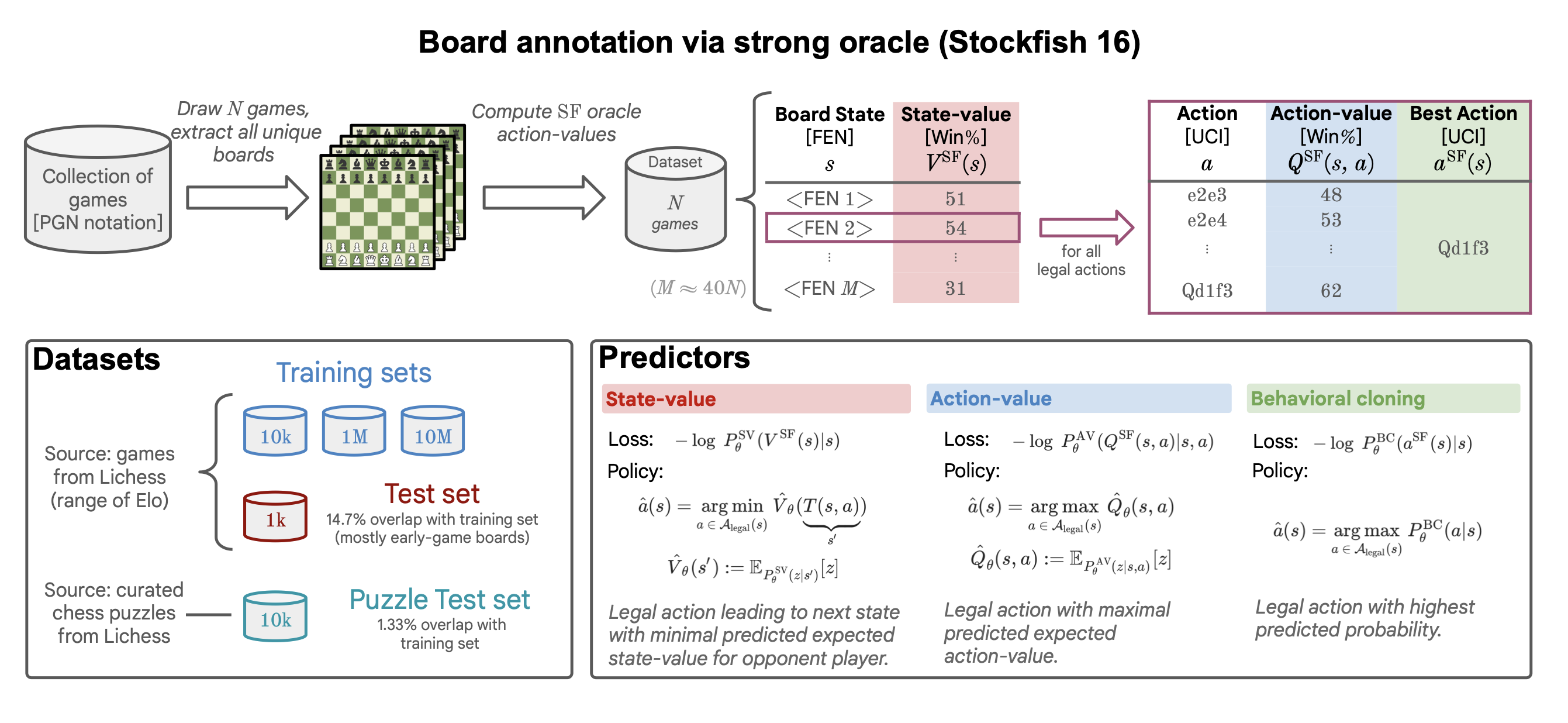
2.1. Data

Acquisition step

1. Download 10M games from lichess.org
2. Extract all board state $s$ from each games
3. Estimate the state-value $V^{SF}(s)$ for each state with Stockfish 16 (with 50ms time limit, unbounded depth and level)
   • Value of a state is the win percentage estimated by Stockfish, lying between 0% and 100%
4. Estimate the action-values $Q^{SF}(s, a)$ for all legal actions $a \in \mathcal{A}_{legal}(s)$ in each state.
   • time limit of 50ms per state-action pair (unbounded depth and max skill level)
   • corresponds to an oracle Lichess blitz Elo of 2713
5. Get oracle best action $a^{SF}$, $a^{SF} = \argmax_{a \in \mathcal{A}_{legal}(s)} Q^{SF}(s, a)$
6. Randomly shuffle dataset for training with individual board(state)

• Drop timeout data from the behavioral cloning training set

Size

Training

• 15.32B action-value estimates
• 530 state-value estimates and best oracle actions

Test

• 1.8M action-value estimates and 60K state-value estimates and best oracle actions from 1K examples of other months
• 14.7% consists of those in training set, do not remove

Puzzle test set

• consisting of 10k challenging board states that come with a correct sequence of moves to solve the puzzle

Value Binning

• The predictors are discrete discriminators (classifiers)
• Convert win-percentages into discrete classes via binning (for state or action values)
• Divide the interval between 0% and 100% uniformly into 𝐾 bins (K=128)
• Assign a one-hot code to each bin

2.2. Model

• Modern decoder-only transformer backbone
• parameterize a discrete probability distribution by normalizing the transformer’s outputs with a log-softmax layer => outputs log probabilities.

Context Size

• 79 for action-value prediction
• 78 for state-value prediction and behavioral cloning

Output size

• 𝐾 (the number of bins) for action and state value prediction
• 1968 (the number of all possible legal actions) for behavioral cloning

More details

• Learned positional encodings (len of input seq is constant)
• 270M parameters for largest model

2.2.1. Tokenization

• Board states $s$ are encoded as FEN strings

FEN strings

are description of

• all pieces on the board
• whose turn it is
• the castling availability for both player
• a potential en passant target
• a half-move clock and a full-move counter

always starts at rank 1, even when it is the black’s turn (never flip the board)

Tokenization

• Turn FEN string to 77 length string of ascii-code
• Then sort all possible legal action of 1968, and take the action’s index as the token

2.2.2. Training Protocols

• Predictors minimize cross-entropy loss
• Uses Adam optimizer
• Train for 10M steps (2.67 epochs for a batch size of 4096 with 15.32B data points)

Target labels (one-hot encoding)

• bin-indices (state- or action-value prediction)
• action indices (behavioral cloning)

2.3. Predictors and Policies

2.3.1. (AV) Action-value prediction

Target

• bin $z_i$ into which the ground-truth action-value estimate $Q^{SF}(s, a)$ falls

Input

• concatenation of tokenized state and action

2.3.2. (SV) State-value prediction

Target

• bin $z_i$ that the ground-truth state-value $V^{SF}(s)$ falls into

Input

• tokenized state

2.3.3. (BC) Behavioral cloning

Target

• The target label is the (one-hot) action-index of the ground-truth action $a^{SF}(s)$ within the set of all possible actions

Input

• tokenized state

2.4. Evaluations

2.4.1. Action-accuracy

• The test set percentage where the predictor policy picks the ground-truth best action

2.4.2. Action-ranking (Kendall’s $\tau$)

• The average Kendall rank correlation (a standard statistical test) across the test set
• correlation of the predicted actions with the ground-truth ranking by Stockfish in each state

2.4.3. Puzzle-accuracy

• puzzles from a collection of Lichess puzzles that are rated by Elo difficulty from 399 to 2867
• percentage of puzzles where the policy’s action-sequence exactly matches the known solution action-sequence

2.4.4. Game playing strength (Elo)

• Get Elo rating with 2 approaches

1. Play Blitz games on Lichess against either only humans or only bots
2. Run an internal tournament between all the agents tested

2.5 Baselines

• Stockfish 16 (oracle)
• AlphaZero (3 variants) (27.6M parameters and are trained on 44M games)
  • the original with 400 MCTS simulations
  • only the policy network
  • only value network
• GPT-3.5-turbo-instruct

notes

• baselines have access to the whole game history
• the paper's model only observe the current game state

3. Results

3.1. Main Results

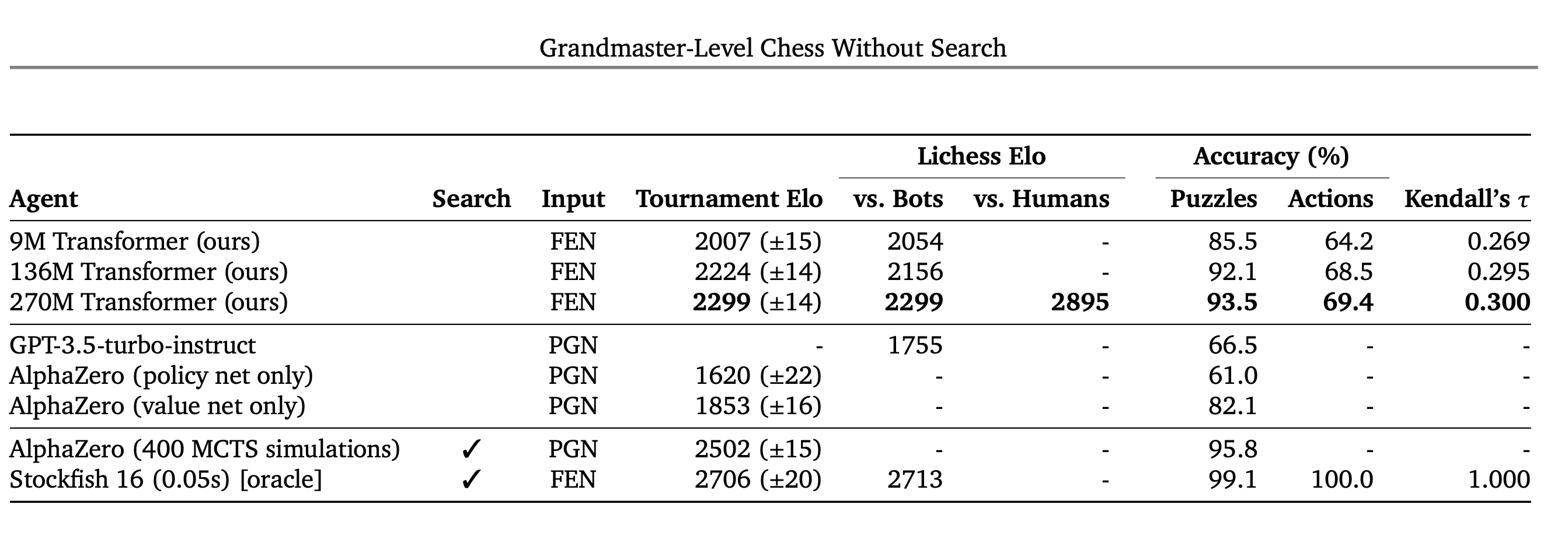
• Largest model achieves a blitz Elo of 2895 against human players(grandmaster level)
• Elo drops when playing against bots on Lichess
  • Maybe result of different player pool, qualitative difference in how bots exploit weaknesses compared to humans

3.2. Puzzles

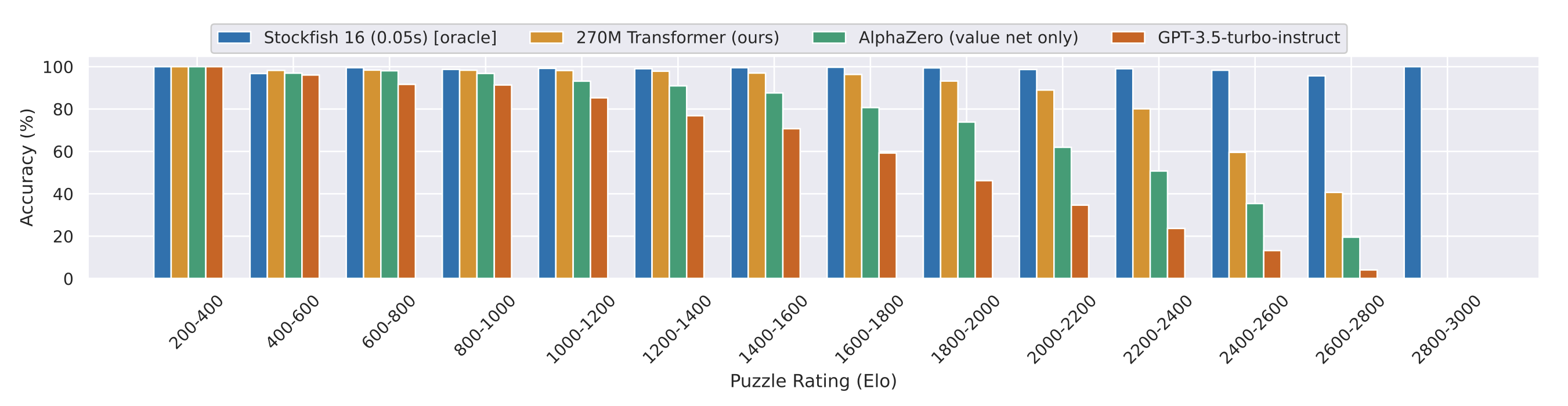
• comes 2nd after Stockfish 16

Emphasized

• Solving the puzzles requires a correct move sequence.
• This policy cannot explicitly plan ahead

=> solving the puzzle sequences relies entirely on having good value estimates that can be used greedily.

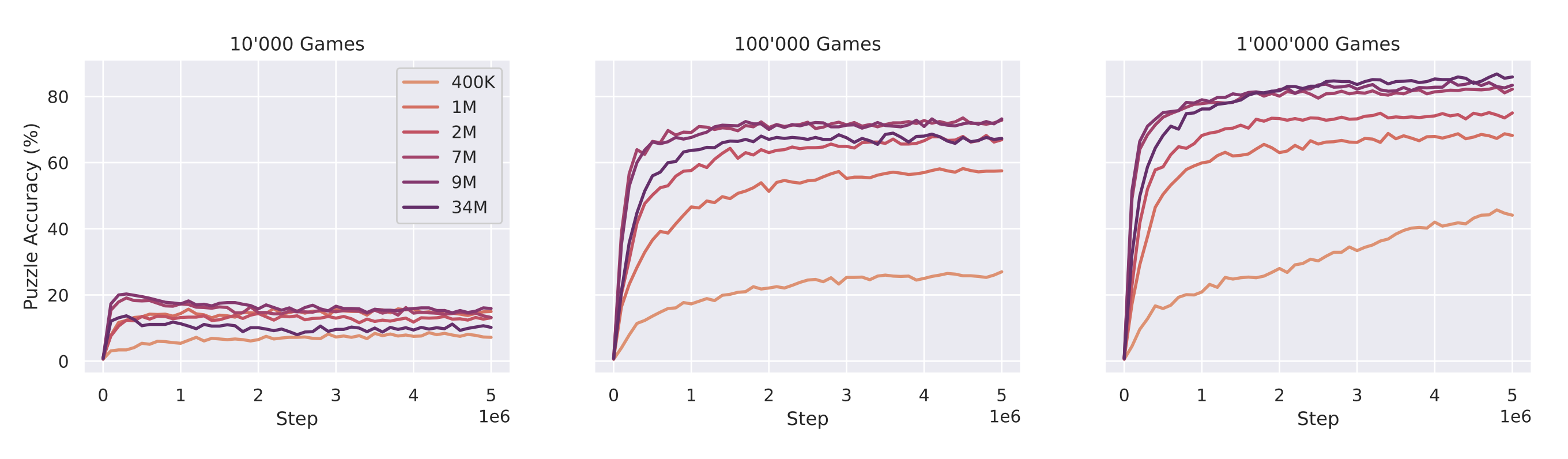
3.3. Scaling laws

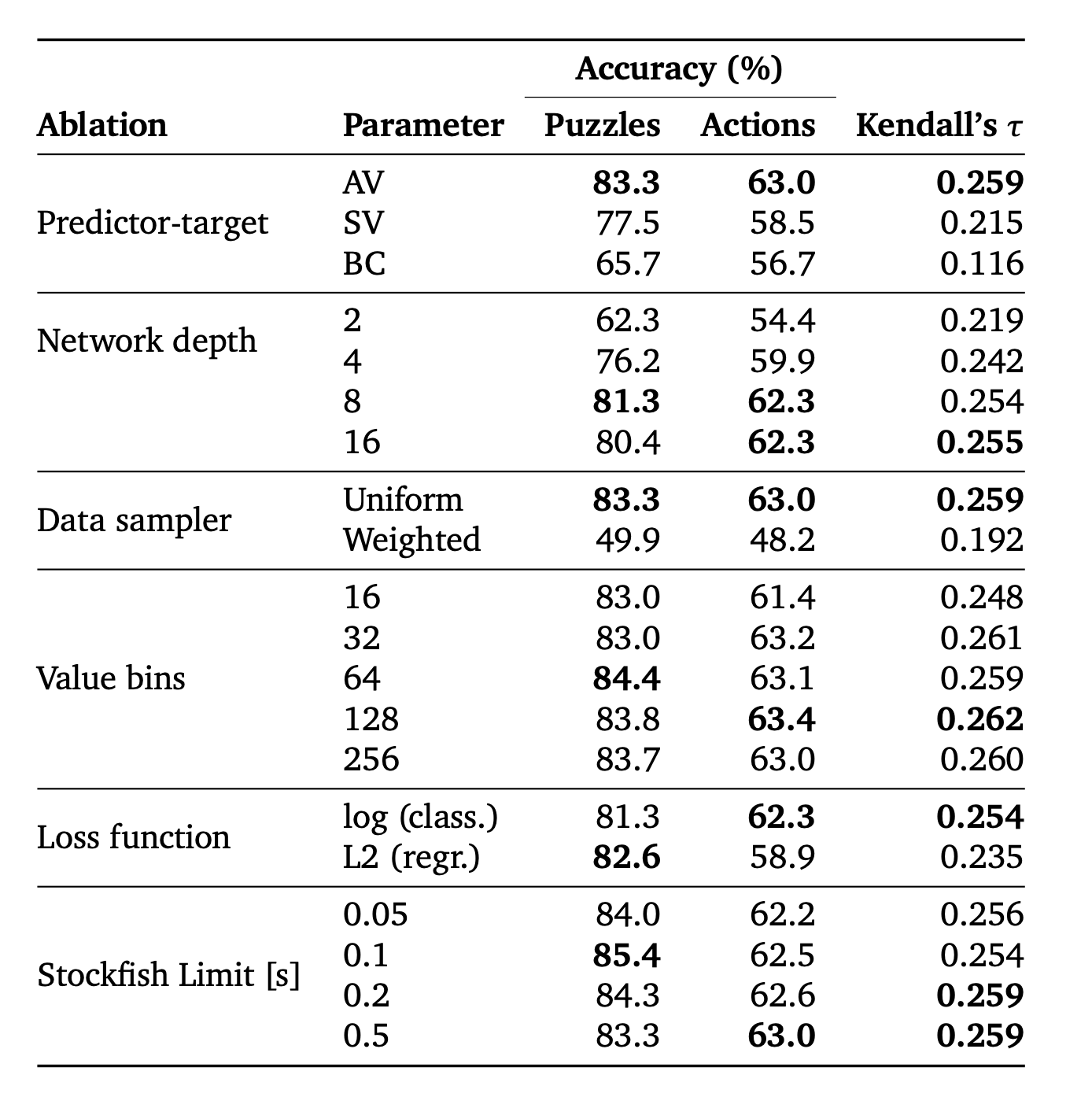
3.4. Variants and Ablations

5. Discussions

2 issues

I. Blindness to threefold repetition

• state-based predictor cannot detect the risk of threefold repetition (drawing because the same board occurs three times)
• FEN has no history info
• Checking if the bot’s next move would trigger the rule and set the corresponding action’s win percentage to 50% before computing the softmax didn't solve the issue.

II. Indecisiveness in the face of overwhelming victory

• If Stockfish detects a mate-in-𝑘 (e.g., 3 or 5) it outputs 𝑘 and not a centipawn score.
• Mapped all such outputs to the maximal value bin (i.e., a win percentage of 100%)
• This can lead to the agent playing somewhat randomly, rather than committing to one plan that finishes the game quickly
• The authors made the model to check whether the predicted scores for all top five moves lie above a win percentage of 99% and double-check this condition with Stockfish, and if so, use Stockfish’s top move (out of these) to have consistency in strategy across timesteps

5.1. Limitations

• Model does not completely close the gap between Stockfish 16.
• Fundamental issue related to current-state based prediction
• State-value predictor uses kind of 1 step search for finding all possible subsequent states that are reachable. => cannot say 'search-free'
  

6. Conclusions

• It is possible to distill an approxi- mation of Stockfish 16 into a feed-forward transformer via standard supervised training
• Implies a paradigm-shift away from viewing large transformers as “mere” statistical pattern recognizers to viewing them as a powerful technique for general algorithm approximation.