Transformers are Multi-State RNNs

Abstract

• Decoder-only transformers can be conceptualized as infinite multi-state RNNs
  * Multi-state RNNs: an RNN variant with unlimited hidden state size

• Pretrained transformers can be converted into finite multi-state RNNs by fixing the size of their hidden state
  -> several existing transformers cache compression techniques can be framed as such conversion policies

• Novel and simple policy TOVA

• TOVA outperforms all other baseline policies, is nearly on par with the full(infinite) model with $1\over8$ cache size.

• Transformer decoder LLMs often behave in practice as RNNs.

Introduction

Decoders

• Decoders became a dominant transformer variant (LLaMA-2, Mistral..)
• Generate output auto-regressively (gen of each token depends on the key and value computation of previous token)
• Aligns with the core principle of RNNs—preserving a state from one step to the next one.

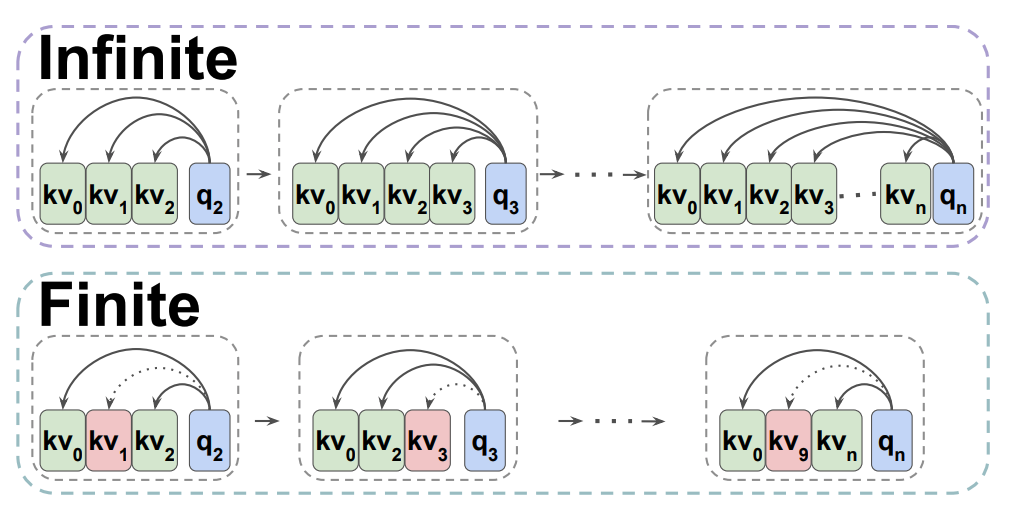
MSRNN(Multi-State RNNs)

• formally redifine decoder-only transformers as as form of MSRNNs.
• Generalized version of traditional RNNs.
• transformers correspond to MSRNNs with an infinite number of states
• transformers can be compressed into finite MSRNNs by limiting the number of tokens processed at each step
  

TOVA

• related to compression policies that effectively limit this capacity in pretrained transformer-based LLMs
• TOVA is simpler and more powerful MSRNN compression policy
• Selects tokens to keep based solely on tokens' attention score
• TOVA outperforms all existing policies + minimal performance degradation

Trained as infinite MSRNNs, Perform as finite MSRNNs.

• not all recent tokens are important to keep in memory
• Importance of keeping the very first token in the sequence

Backgrounds

RNNs

• Can be formulated as $x_{t}^{l+1},h_l^t = f^l_{RNN}(x_t^l,h^l_{t-1})$
• $l$-> layer number, $f^l_{RNN}$ -> layer's model(cell)
• $h$ -> hidden state

Transformers

• takes input as sequence of token representations: $X^l = (x_1^l, ...,x^l_t)\in\mathbb{R}^{t\times d}$
• returns a transformed representation $X^{l+1}=f^l_{\text{TRANS}}(X^l)=\text{FF}^l(\text{SelfAttn}^l(X^l))$

Decoders

• Mask the upper triangular part of the attention matrix.
• Common to cache the K, V matrices to avoid recomputing the previous tokens

Transformers as Multi-State RNNs

Multi-State RNN

• RNN with a state matrix($H\in \mathbb{R}^{g(t)\times d}$) instead of a vector($h$)
• $x_{t}^{l+1},H_l^t = f^l_{MSRNN}(x_t^l,H ^l_{t-1})$
• Each row of $H_l^t$ can be interpreted as a single-state.
• If $g(t)=1$, the MSRNN is standard RNN

Transformers are infinite MSRNNs

• $H_t^l=(K_t^l, V_t^l)$

• layer computation is

• $(K_t^l, V_t^l)= \left(\left( \begin{matrix}K^l_{t-1}\\ k^l_t\end{matrix}\right ),\left(\begin{matrix}V^l_{t-1}\\ v^l_t\end{matrix} \right )\right )$

• $x_t^{l+1} = \text{FF}^l(\text{Attn}^l(q_t^l, K^l_t, V^l_t))$

• q, k, v are the self-attention projections of x, and each single-state of K, V corresponds to a specific token

• MSRNN equation for transformers: $x_t^{l+1}, (K^l_t, V^l_t)=f^l_{\text{TRANS}}(x^l_t, (K^l_{t-1}, V^l_{t-1}))$

• In practice, transformer models are trained up to a specific length and often struggle.

• In theory, they possess the capacity to handle infinite-length inputs, and thus correspond to an infinite size MSRNN

Converting Pretrained Transformers into Finite MSRNNs

• Do pretrained transformers actually make use of this infinite capacity?
• Define a finite MSRNN by setting $g(t)=\text{min}(t, k)$ (k is constant)
• Several compression policies are like this.

Window

• FIFO strategy
• When multi-state reaches capacity limit, the oldest stage(the earliest token) is discarded

Window + $i$

• Extention of the Window policy which retains the first $i$ tokens
• Strongly outperforms Window with as few as four early tokens

H$_2$O

• Dynamically selects the none window tokens by aggregating the attention scores throughout the sequence and keeping the tokens with highest aggregated scores.
• Number of non-window tokens is typically set as half of the multi-state size.

TOVA (Token Omission Via Attention)

• Retains the top states based on the attention weights of the last token only.
• Consider attention scorers from the current query to all the tokens currently in the multi-state, plus the current token at each decoding step.
• The token with the lowest score is dropped.
  
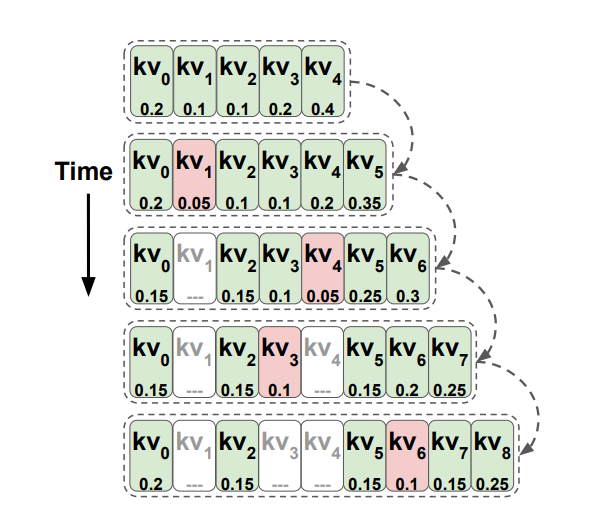
• Makes fewer assumptions compared to the existing policies. (neither fixes a window of recent tokens, nor favors early tokens)
• Weak recency bias (early tokens require high attention scores in all subsequent decoding steps to be kept in the multi-state)
• However, substantial fraction of the recent tokens are dropped by TOVA => suggesting that fixed recent window is too strict

Experiments

• Input length: 4096 tokens

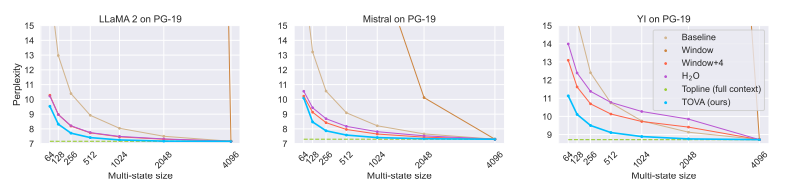
Language modeling

• LLaMA-2, Mistral, Yi (~7B version)
  

Long range understanding

• LLaMA-2-chat, Mistral-Instruct, neural-chat
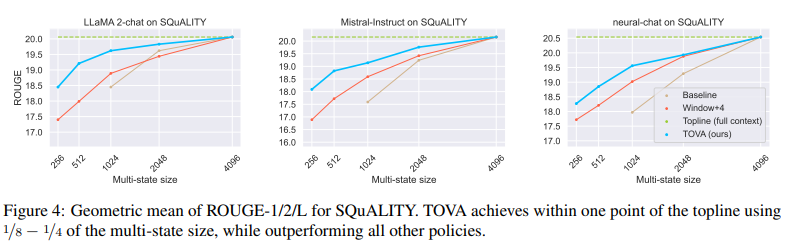  => Long range summarization
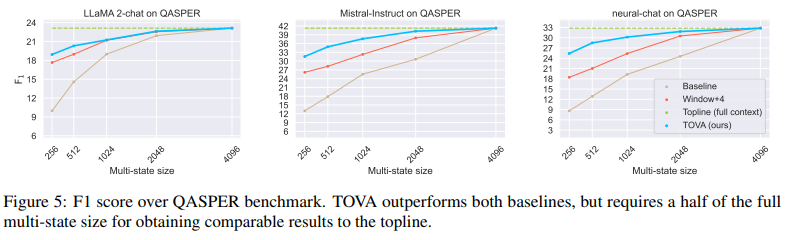  => Long range QA

Text generation

• MythoLogic(LLaMA-2-13B version fine-tuned for story generation)
  

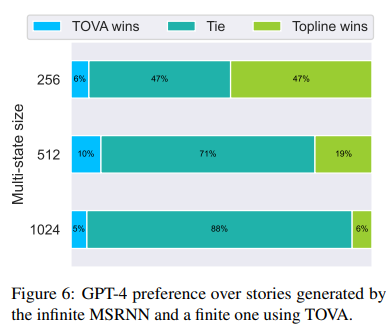
Results

• Transformer decoder LLMs often behave empirically as finite MSRNNs.
• It shares difficulties of retrieval of long range information with RNNs

Analysis

Which Tokens Matter?

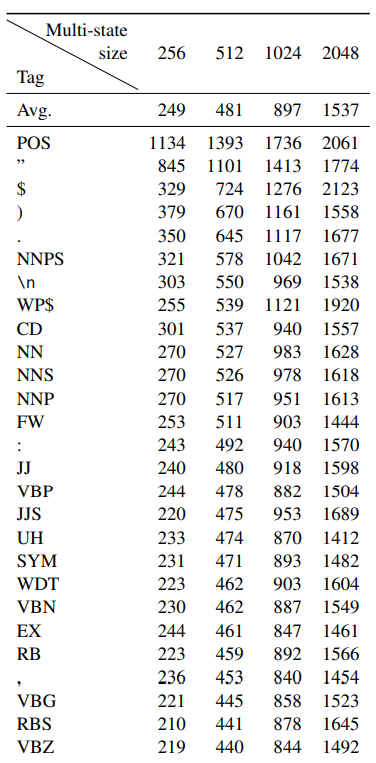
• Analysis using LLaMA-2-7B, PG-19
  

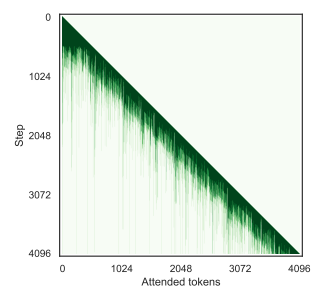
Recency is not all you need

• only 73~76% of the tokens are recent

First token matters

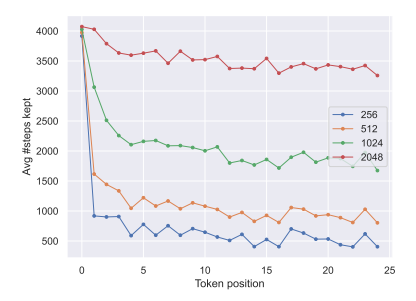
Not all tokens are equally kept

• Punctuation and other special symbols tend to be kept
• Possessive nouns(POS) and proper nouns(NNPS) tend to stay longer
  

Increased Batch size using TOVA