While working on a project in my lab, I saw that XGBoost and LightGBM outperforms any deep learning implementation. This led to the search of TabNet. But while TabNet has shown that deep learning can work well on tabular data, GBDT based models dominate the real world applications of AI. Second paper, "Tabular data: Deep Learning is not all you need" shows why this is happening.

TabNet: Attentive Interpretable Tabular Learning (19'Arxiv, 21'AAAI)

Work by Sercan O. Arık, Tomas Pfister @ Google Cloud AI

Abstract

• High performance & Interpretable deep tabular data learning architecture
• Sequential Attention choosing features at each decision step
• Self-superivised learning for tabular data

Introduction & Backgrounds

• DNNs are yet to show success in tabular data.

Tabular data

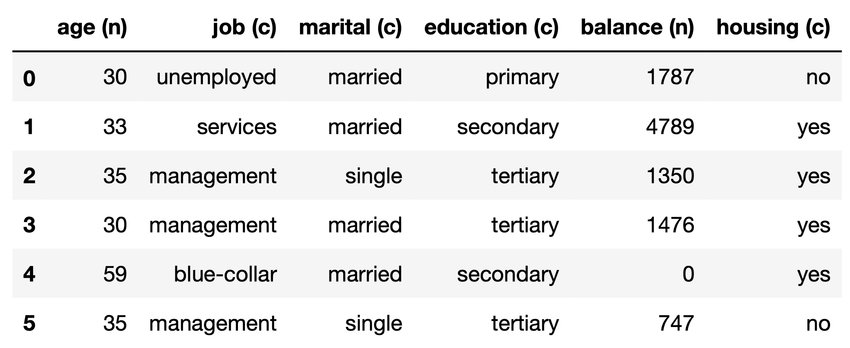
• Data containing categorical and numerical features

The reason DTs are better than DNNs

1. DT-based approaches have certain benefit
   • representionally effficents for approximating hyperplane boundaries (common in tabular data)
   • highly interpretable (tracking decision nodes)
   • fast to train
2. previously-proposed DNN architectures are not well-suited
   • CNNs & MLPs are overparametrized (lack of inductive bias)

The reason DNNs approach is nessasary

• Scalability: Can use multiple data types like images
• Alleviating the need for feature engineering
• Learning from streaming data
• End-to-end models allow representation learning(generative modeling, semi-supervised learning)

Tree-based learning

• Ensembling to reduce varaince
• Random Forests(Ho 1998), XGBoost(Chen 2016), LightGBM(Ke at al. 2017)

TabNet's main contributions

1. End-to-End learning
   • Inputs raw data without any preprocessing
   • trained using gradient descent
2. Interpretability
   • sequential attention to choose which features to reason from at each decision step
3. Performance (From 1, 2)
   • Outperforms(or on par) with other models
   • Local interpretability & Global interpretability
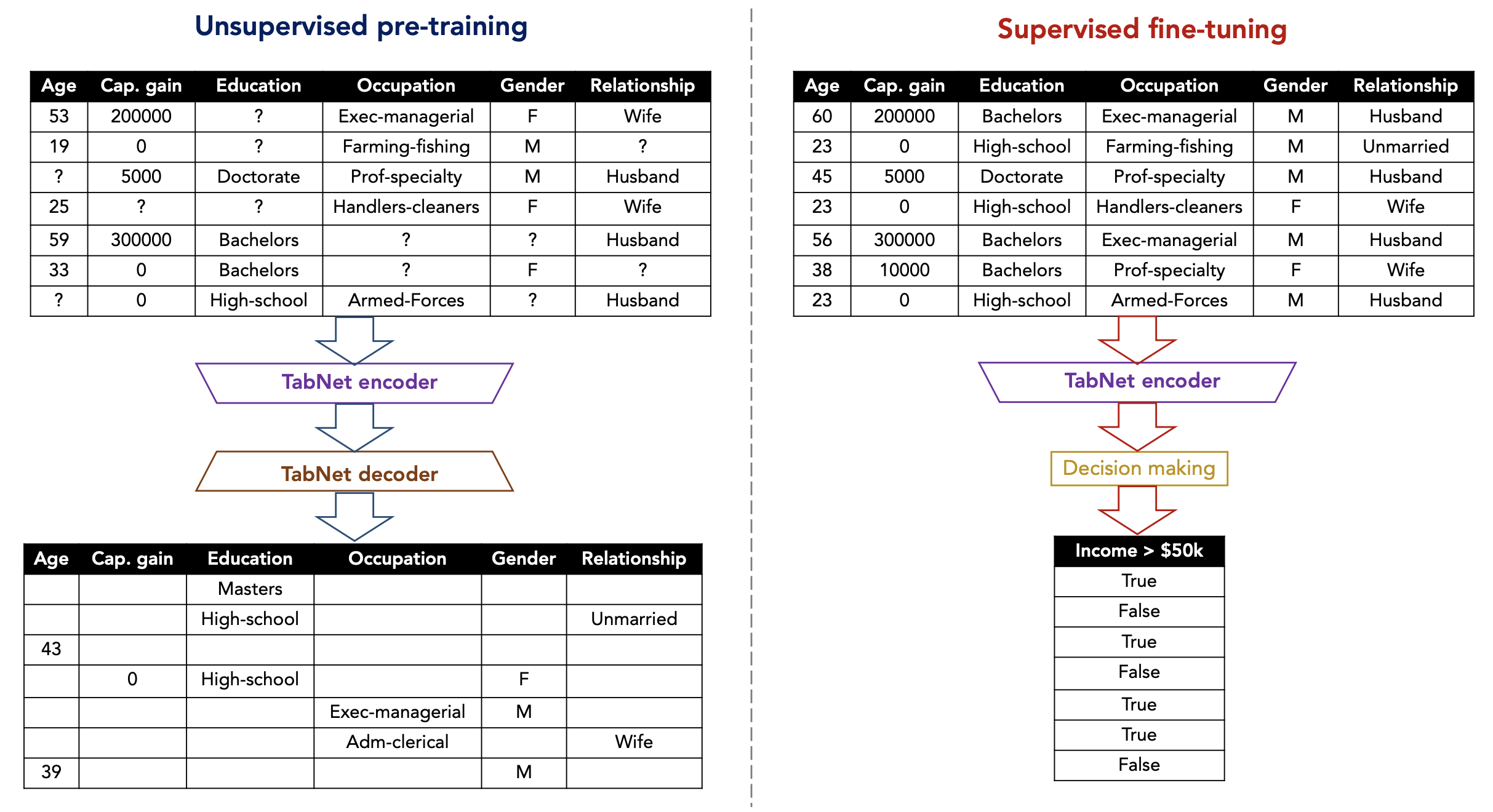
4. Unsupervised pre-training
   • first time for tabular data
   • significant performance improvements

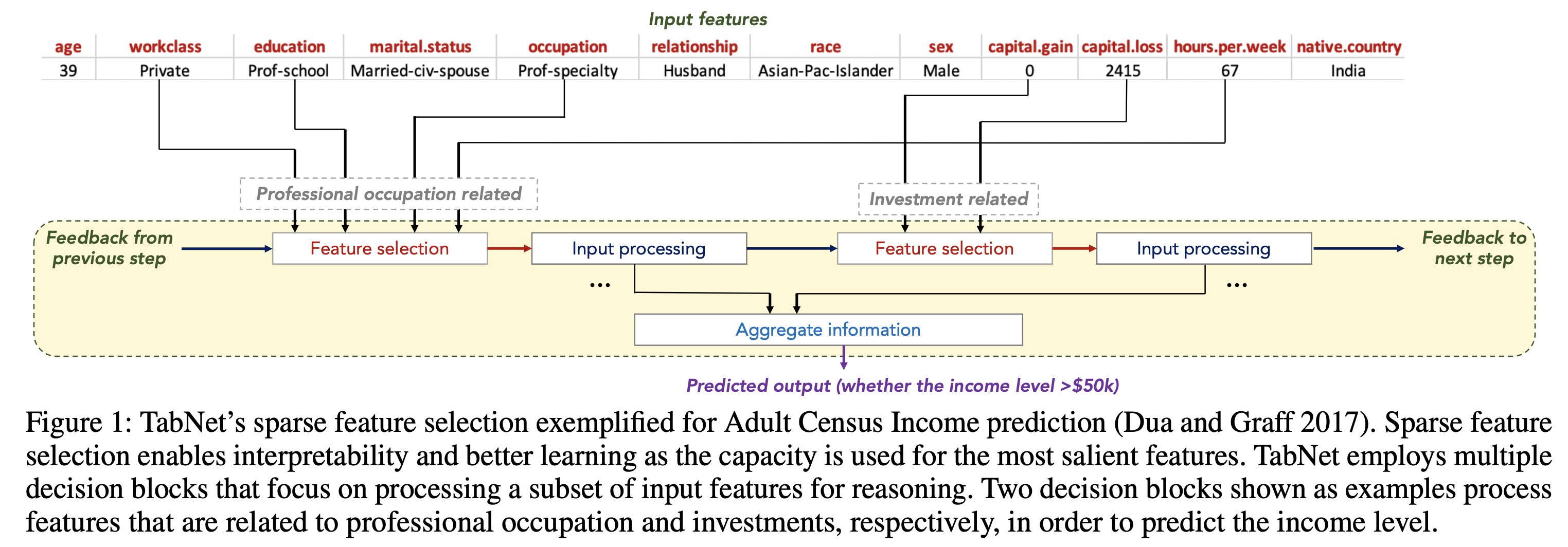
TabNet for Tabular Learning

DT like DNN?

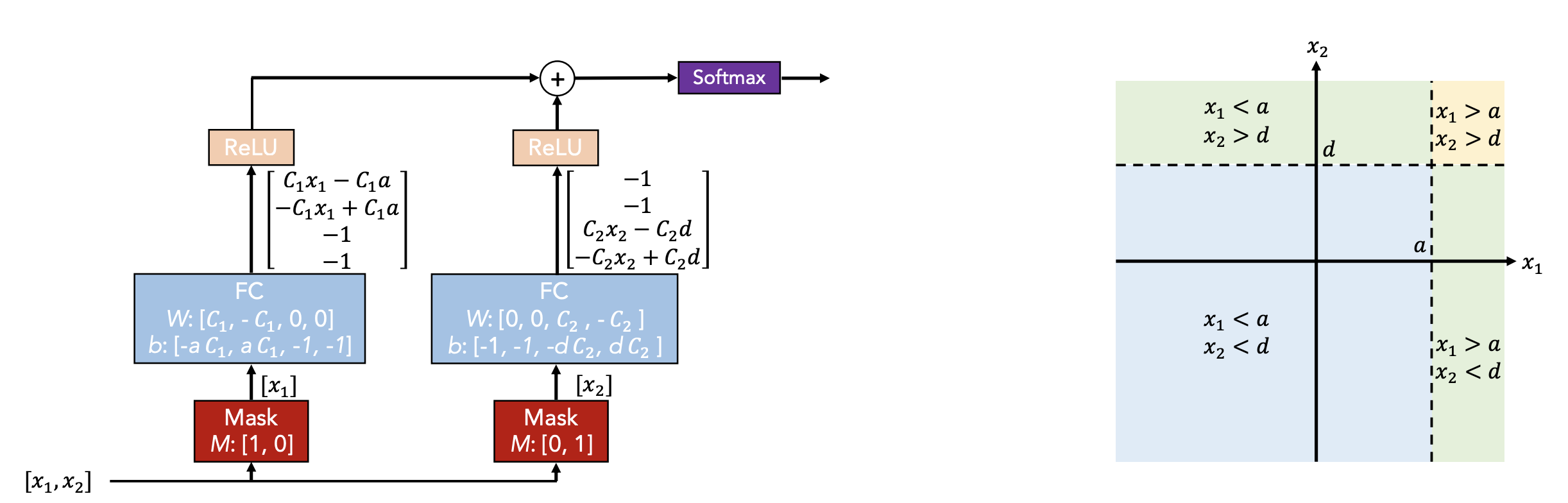
Highlighted Points of model

• Use sparse instance-wise feature selection learned from data
• Constructs a sequential multi-step architecture (each step contributes to a portion of decision based on the selected feature - DT's benefits
• Improves learning capacity via non-linear processing of the selected features
• Mimics ensembling via higher dimensions and more steps

TabNet Encoder Architecture

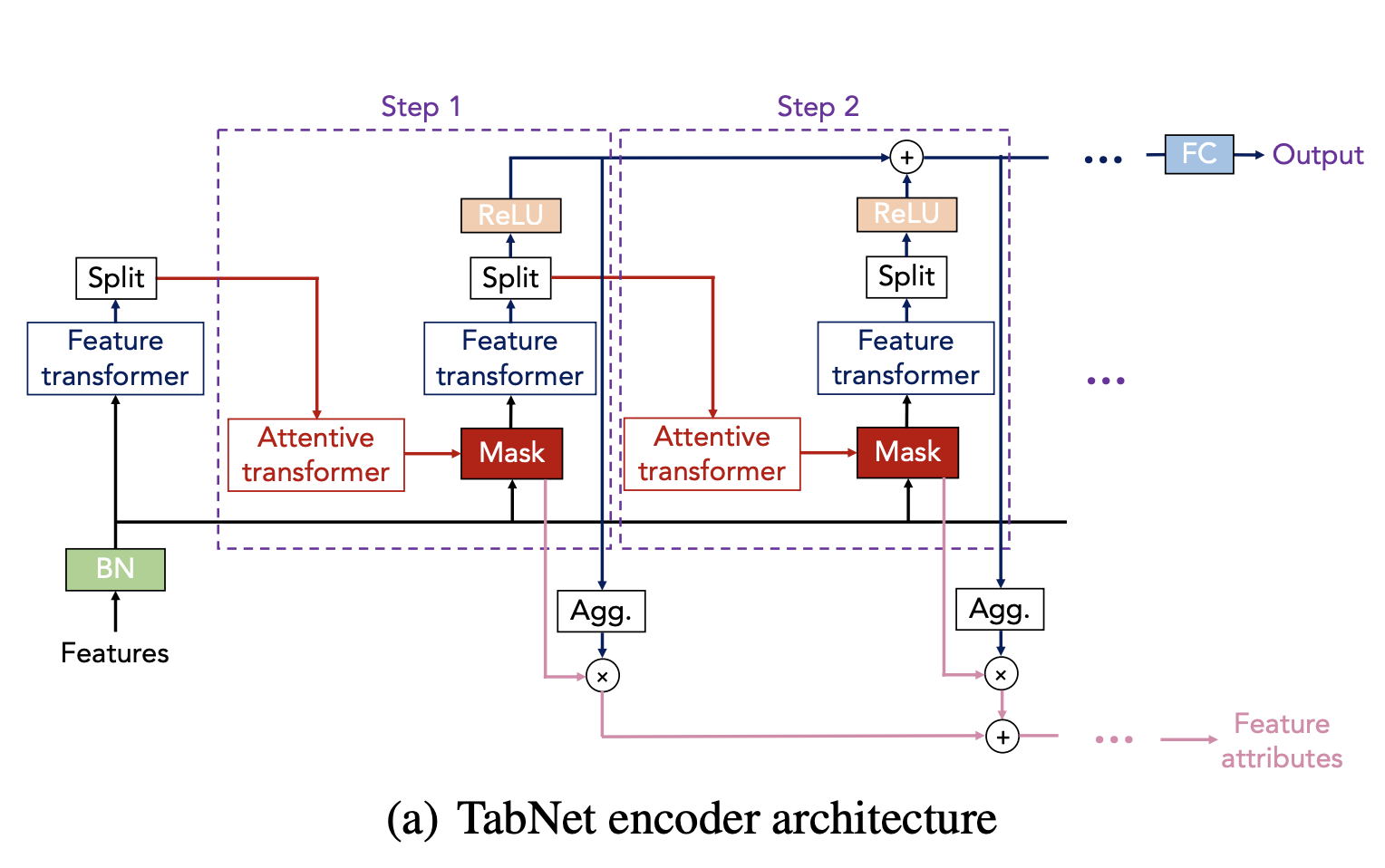
• use raw numerical features
• consider mapping of categorical features with trainable embeddings
• $\mathbf{f} \in \mathbb{R}^{B \times D}$ is passed at each decision steps
• Sequential multi-step processing with $N_{steps}$ decision steps
• ith step uses information from (i-1) step and decides which feature to use
• each feature representation is aggregated into output

Feature selection

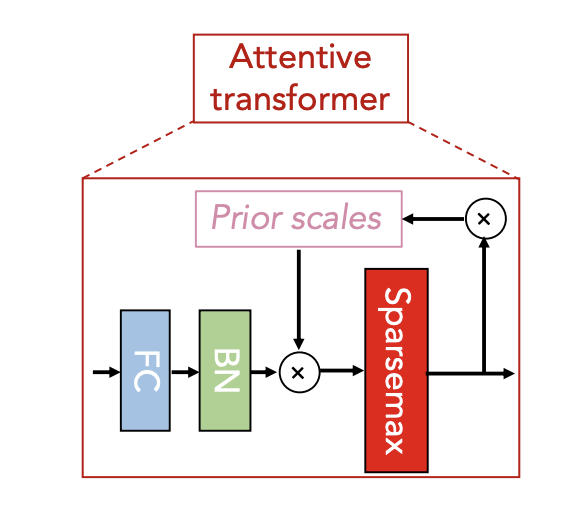
• Learnable Mask $\mathbf{M}[\mathbf{i}] \in \mathbb{R}^{B \times D}$
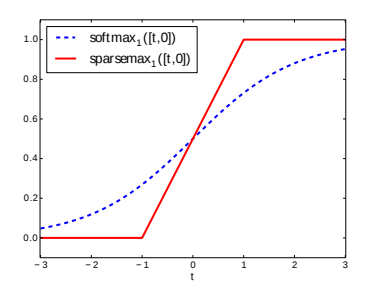
• Soft selection of the salient features.
• Models become for parameter efficient
• Attentive Transformers inputs $\mathbf{a}[\mathbf{i-1}]$ (processed feature of i-1 step) and outputs mask with $\mathbf{M}[\mathbf{i}] = \text{sparsemax}(\mathbf{P}[\mathbf{i-1}] \cdot \text{h}_i(\mathbf{a}[\mathbf{i-1}])$
• Sum of each row in a mask is 1.
• $\text{h}_i$ is FC -> BN in the figure.
• $\mathbf{P}[\mathbf{i}]$ is prior scale term.
• $\mathbf{P}[\mathbf{i}]=\prod_{j=1}^i(\gamma-\mathbf{M}[\mathbf{j}])$.
• $\gamma$ is relaxation parameter. (if $\gamma =1$ , a feature can be used at most once for each decision step)
• $\mathbf{P}[\mathbf{0}]$ initialized to all 1.
• Sparcity regularization coefficient $\lambda_{sparse}$ to the overall loss

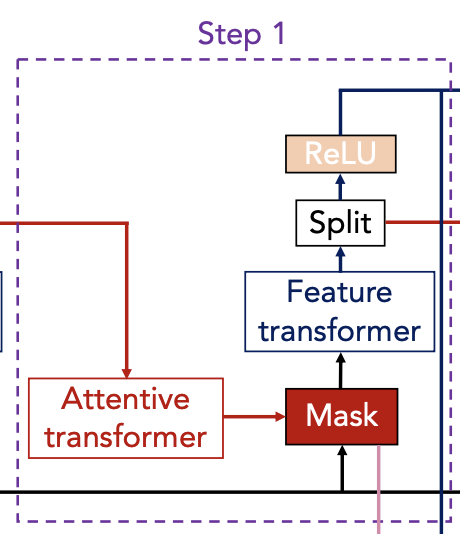
Feature processing

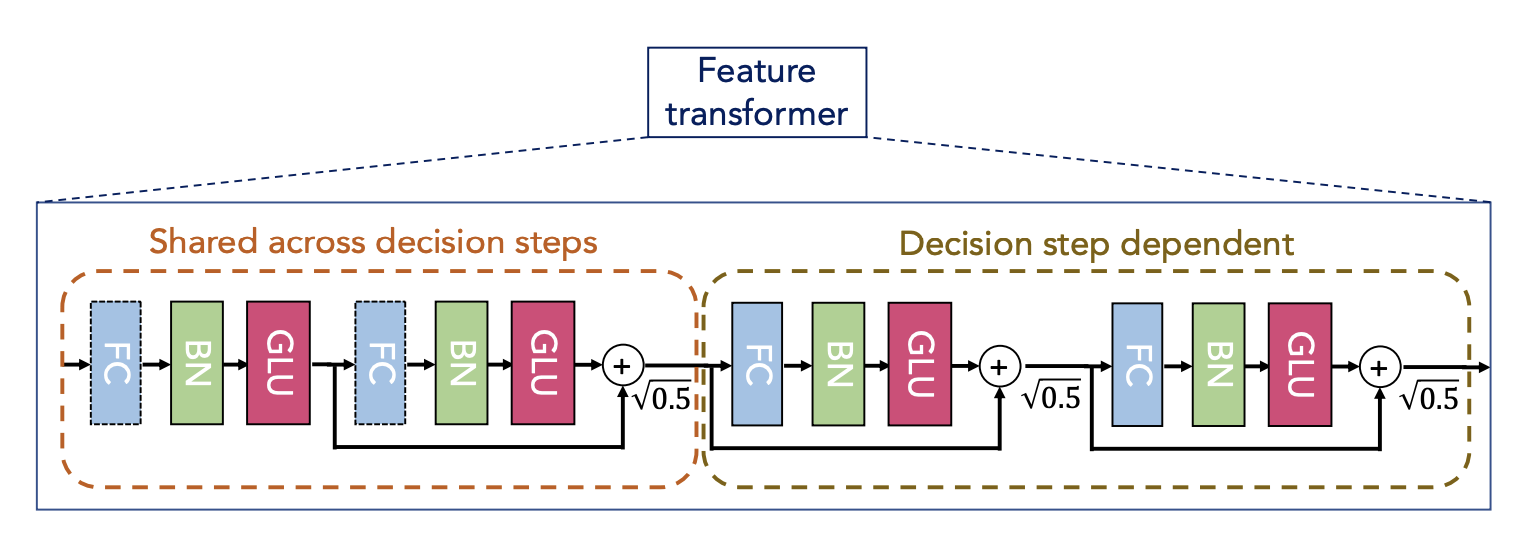• Process filtered feature with feature transformer
• Split the output: $[\mathbf{d}[\mathbf{i}],\mathbf{a}[\mathbf{i}]]=\text{f}_i(\mathbf{M}[\mathbf{i}] \cdot \mathbf{f})$
• d[i] is used for decision step, a[i] is used for next step
• Dimension of d and h are hyperparameters (one of 8, 16, 24, 32, 64, 128)
• Same features are input across the model -> Shared part for parameter-efficient and robust learning with high capacity
• 2 Shared layers + 2 decision step dependant layers
• FC-BN-GLU
• nomalized residual with $\sqrt{0.5}$
• Overall decision embedding $\mathbf{d_{out}}=\sum_{i=1}^{N_{steps}}\text{ReLU}(\mathbf{d[i]})$
• Inspired by decision-tree like aggregation
• Final output mapping $\mathbf{W_{final}d_{out}}$

Interpretability

• Since mask value correspond to the feature importance, combine outputs in linear way
• Weights of each masks $\eta_{\mathbf{b}}\mathbf{[i]}=\sum_{c=1}^{N_d} \text{ReLU}(\mathbf{d_{b,c}}\mathbf{[i]})$.
• Aggregate feature importance mask $\mathbf{M_{agg-b, j}}:=\sum_{i=1}^{N_{steps}}{{\eta_{\mathbf{b}}[\mathbf{i] M_{b,j}[i]}}\over{\sum_{j=1}^{D}\sum_{i=1}^{N_{steps}}}{\eta_{\mathbf{b}}[\mathbf{i] M_{b,j}[i]}}^2}$
  

TabNet Decoder Architecture for Self-supervised Learning

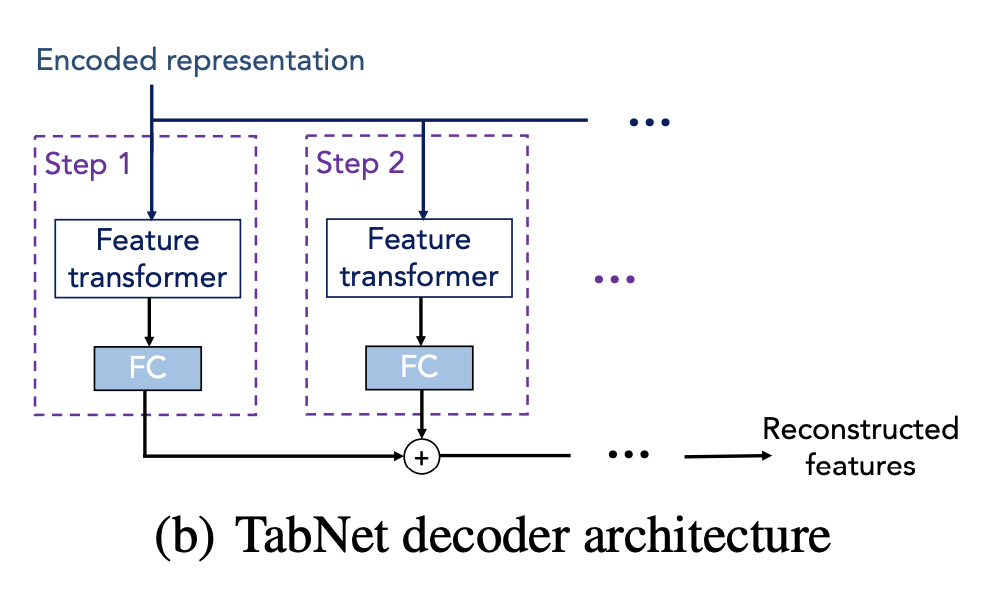
• Task of prediction of missing feature columns from the others

Experiments

• Published benchmarks of regression or classification tasks
• Model performance int not very sensitive to most hyperparameters

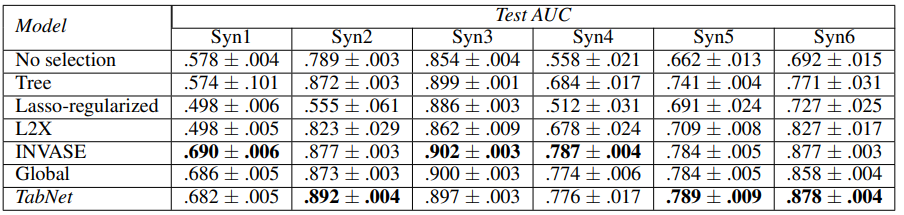
Syn Dataset

• 6 tabular datasets (Syn1 ~ Syn6)
• 10K training samples
• only a subset of the features determine the output
  

Real-world datasets

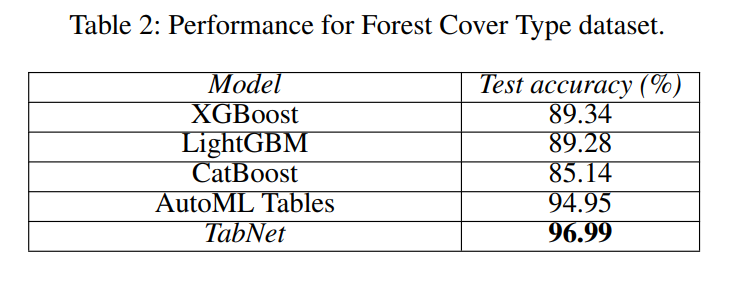
Forest Cover Type

• classification of forest cover type from cartographic variables
  

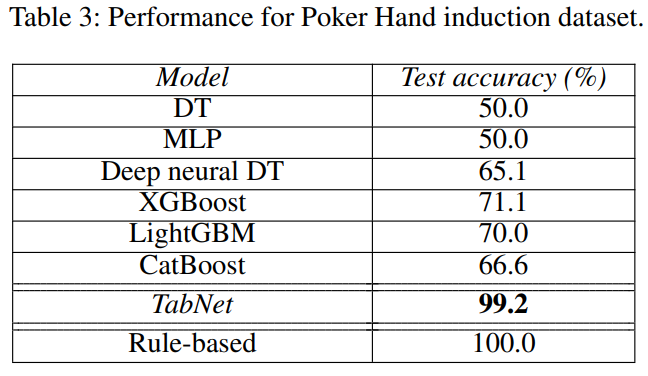
Poker Hand

• deterministic, but imbalanced
  

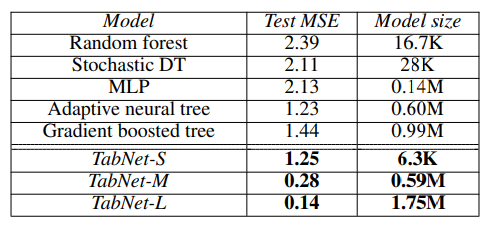
Sarcos

• regressing inverse dynamics of an anthropomorphic robot arm
  

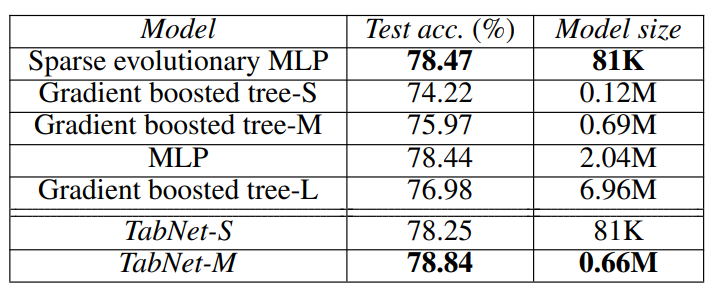
Higgs Boson

• distinguish between a Higgs bosons process vs background
• Much larger size(10.5M instances)
  

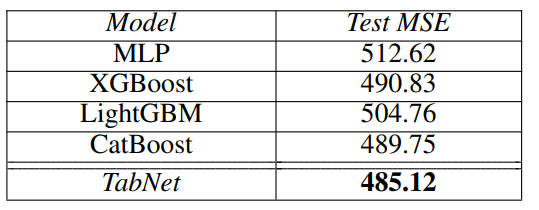
Rossmann Store Sales

• forecasting store sales from static and time-varying features
  

Interpretability

• feature importance consistent with the well-known methods
• assign bigger importance for most discriminative feature ("Odor" in mushroom edibility dataset)

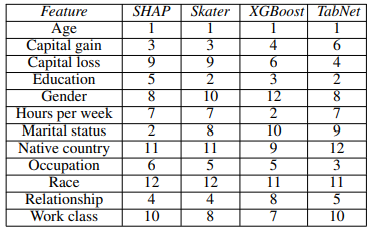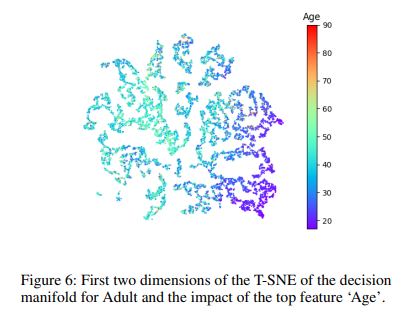Self-supervised learning

• Higgs dataset
• significantly improves performance on the supervised classification dataset
  

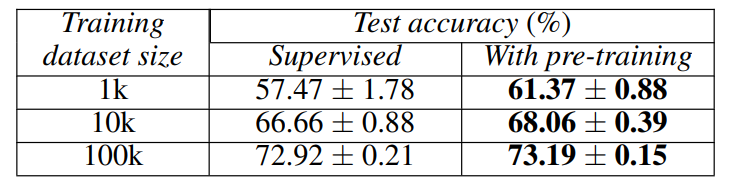
These results show that TabNet is looking like it is setting the field of DNNs in tabular data, but...

Tabular Data: Deep Learning is Not All You Need (21'Arxiv, 22'Information Fusion)

Abstract

• Tree ensemble models are usually recommended for tabular data.

  However, several deep learning models for tabular data have recently been proposed, claiming to outperform XGBoost for some use cases

• Compare the new models to XGBoost on performance, tuning and computation time.

• Results: XGBoost outperforms these deep models across the datasets, including the datasets used in the papers that proposed the deep models + XGBoost requires much less tuning

• Ensemble of deep models and XGBoost performs better than XGBoost alone.

Introduction & Background

Recent attempts of DNNs for tabular data

• [Arik and Pfister, 2021, Katzir et al., 2021, Popov et al., 2020]
• Claimed to outperform GBDT
• Used different datasets (no standard benchmark like ImageNet or GLUE)
• Challenging to compare these models (some lack open-source)
• Often did not optimize the models equally

Main research point

• Accuracy test (especially for datasets not proposed in each paper)
• Time of training and hyperparameter search

Research method

• 4 DNN models
• 11 datasets (9 were used in those papers)

The 4 models

TabNet (Arik and Pfister, 2021)

Neural Oblivious Decision Ensembles (NODE) (Popov et al., 2020)

• Differentiable oblivious decision trees(ODTs)
• split data to seleced features, but only one feature is chosen at each level, resulting in balanced ODT that can be differentiated.

DNF-Net (Katzir et al., 2021)

• Simulate disjunctive normal formulas (DNF: OR-of-ANDs) in DNNs.
• replacing hard Boolean formulas with soft, differentiable versions

1D-CNN (Baosengou, 2021)

• Best single model performance in a Kaggle competition with tabular data
• Still, rarely used because feature ordering has no locality charicteristics.

Comparing the Models

Datasets

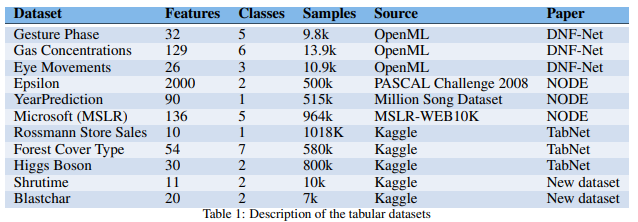
• 9 datasets from the TabNet, DNF-Net, NODE papers + 2 new Kaggle datasets

Optimization process

• HyperOpt for model hyperparameter selection
• Each model had 6~9 main hyperparameters
• Split the data into train, validation, test in the same way as in the original paper
• Check the statistical significance

Results

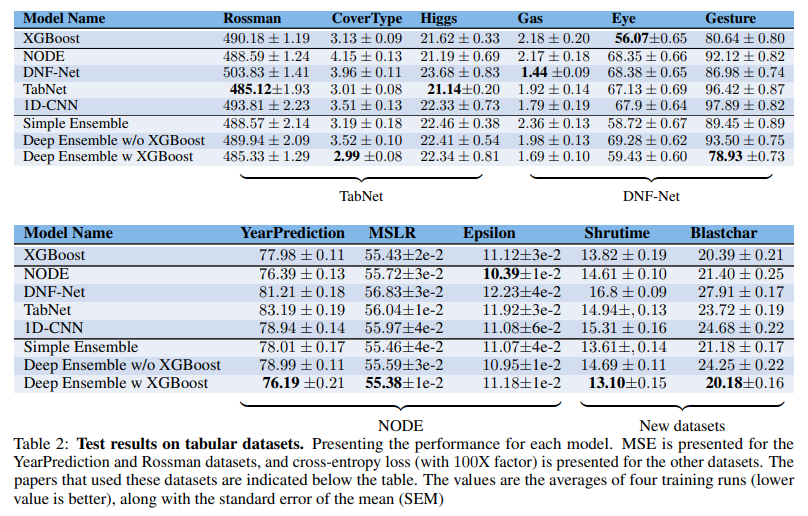
• In most cases, the models perform worse on unseen datasets
• XGBoost model generally outperformed deep models (8 / 11 -> significant for each)
• No deep models consistently outperformed the others. (only performed well on its own datasets)
• 1D-CNN model may seem better (all new dataset)
• Ensemble of deep models and XGBoost outperformed the other models (7/11, significant)

Average Relative Performance

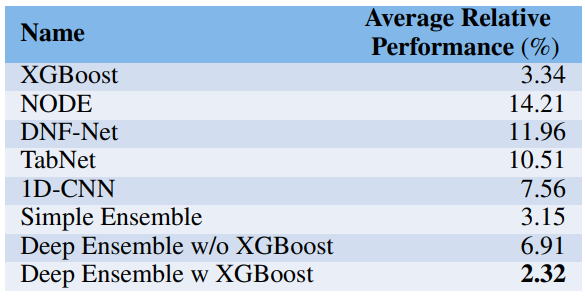
• Performance on unseen dataset

Reasoning

Selection bias

• May demonstrated the model's performance on datasets with which the model worked well.

Difference in optimization of hyperparameters

• May have set the hyperparameter based on a more extensive hyperparamter search on the datasets presented in that paper.

Opimization difficulty search

• FLOPS? -> hard to compute when optimizing hyper parameter
• Compare time? -> not fair(difference in software optimization)
• Compare number of iterations of the hyper parameter optimization process

Result

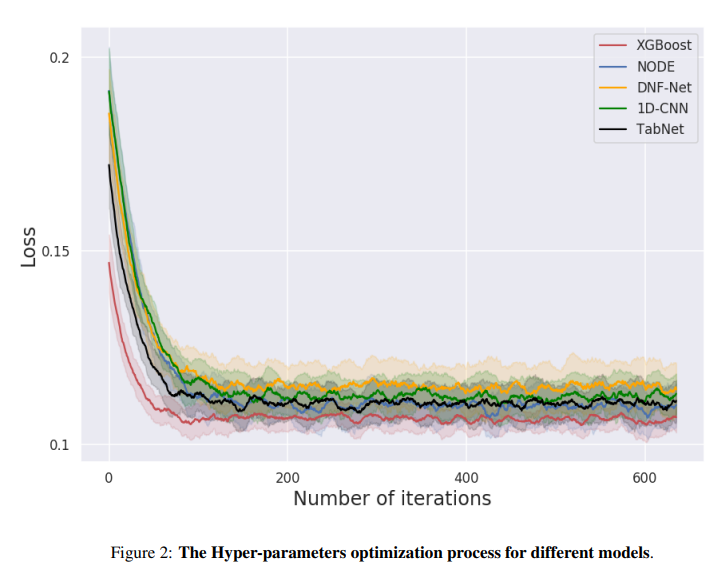
• XGBoost outperformed deep models

Factors

• Bayesian hyperparameter optimization process -> results may differ
• Initial hyperparameter of XGBoost may be more robust
• XGBoost may have some inherent chracteristics that make it more robust and easier to optimize.

Conclusion

• XGBoost outperforms deep models
• Future research on tabular data must systematically check the performance on several diverse datasets
• Improved ensemble results provide potential for further research.