Title

xLSTM: Extended Long Short-Term Memory (arxiv 2024)

Abstract

• 1990s -> Long Short-Term Memory with constant error carousel and gating
• LSTMs -> Contributed to numerous deep learning success stories, with first LLMs.
• Transformer with paralleizable self-attention outpaces LSTMs at scale

  How far do we get in language modeling when scaling LSTMs to billions of parameters, leveraging the latest techniques from modern LLMs, but mitigating known limitations of LSTMs?

• Exponential gating with appropriate normalization and stabilization techniques.
• Modify LSTM memory structure
  • sLSTM: scalar memory, scalar update, new memory mixing
  • mLSTM: fully parallelizable with matrix memory and a covariance update rule
• Integrating s,mLSTM into residual block backbone -> xLSTM blocks -> residually stacked into xLSTM architectures
• Perform favorably in performance and scaling compared to Transformers and State Space Models
  

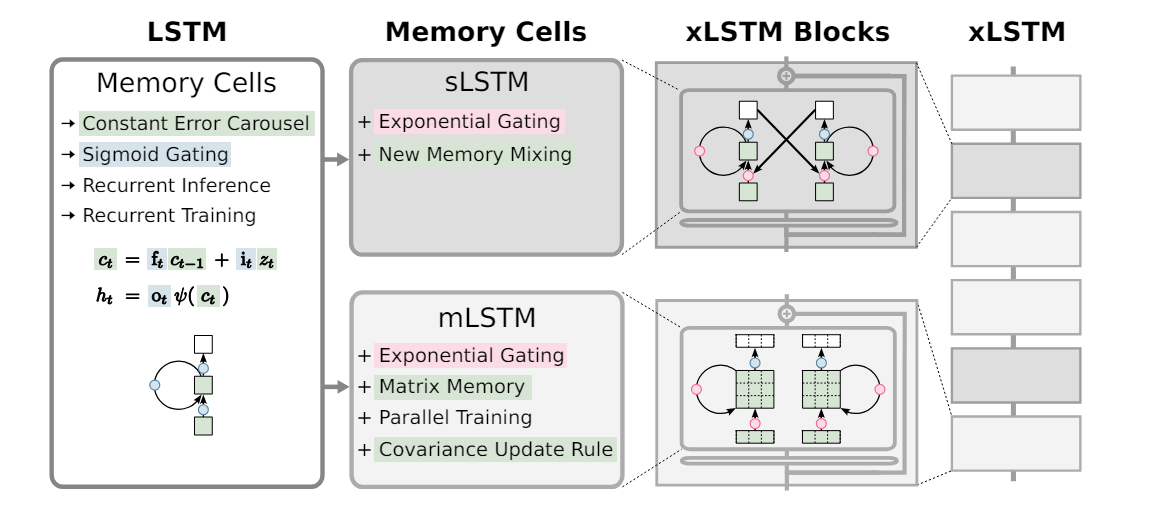
1. Introduction

LSTM

(Hochreiter, 1991; Hochreiter & Schmidhuber,1997)

Architecture

• Constant error carousel and gating to overcome the vanishing gradient problem of RNNs
  
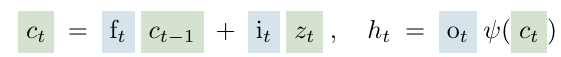
• Constant error carousel -> additive update of the cell state $c_{t-1}$ by cell inputs $z_t$ with sigmoid gates(blue)
• The input gate $i_t$ and the forget gate $f_t$ control the update
• The output gate $o_t$ controls the output of the memory cell(hidden state $h_t$)
• Cell state is normalized or squashed by $\psi$.

History

• successfully applied to various domains
• prevailed over text generation until Transformers in 2017.
• still used in highly relevant applications and have stood the test of time

Limitations

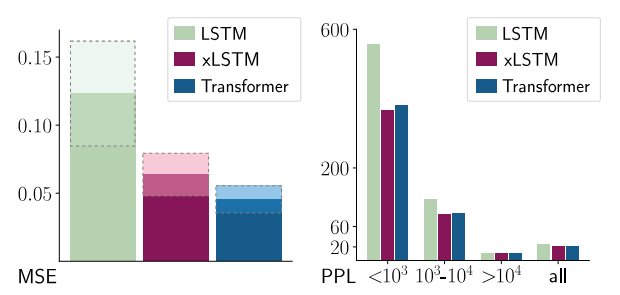
1. Inablity to revise storage decisions
   • Left figure - low performance in Nearest Neighbor Search
2. Limited storage capacities (compressed into scalar cell state)
   • Right figure - low performance in Rare Token Prediction
3. Lack of parallelizability due to memory mixing (enforced sequential processing)

What performances can we achieve in language modeling when overcoming these limitations and scaling LSTMs to the size of current Large Language Models?

2. Extended Long Short-Term Memory

• Main modification -> exponential gating and novel memory structure

2 new LSTMs

• sLSTM -> scalar memory, scalar update, memory mixing
  • exponential gating
  • memory mixing across cells
  • multiple heads with memory mixing across cells within each head
  • new way of memory mixing
• mLSTM -> matrix memory, covariance(outer product) update, parallelizable.
  • exponential gating
  • abandon memory mixing for parallelization

xLSTM

• xLSTM block (redisual block + s/m LSTM)
• stacking xLSTM blocks -> xLSTM architectures.

2.1 Review of the Long Short-Term Memory

• scalar memory cell as a central processing

• storage unit that avoids vanishing gradients

  • with constant error carousel (cell state update)

• memory cell -> input, output, forget gate (forget gate was added by Gers 2000)

LSTM memory update rule at $t$

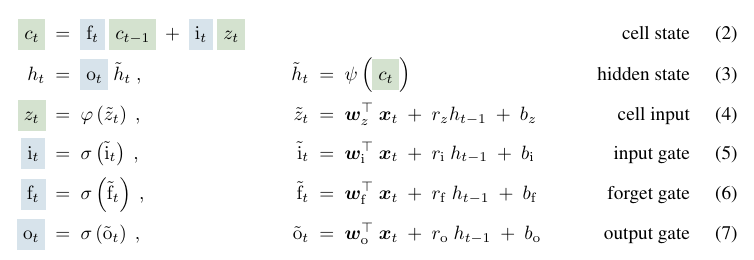
• $w$: input weight vectors
• $r$: recurrent weights between hidden state and cell input, input gate, forget gate, output gate
• $b$: corresponding bias terms
• $\phi$: cell input activation function
• $\psi$: hidden state activation function -> normalize or squash the cell state
• All gate activation function are sigmoid

2.2 sLSTM

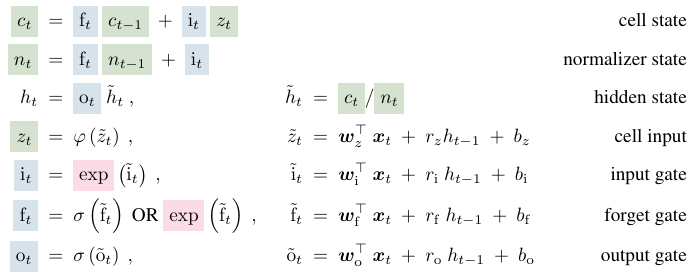
Exponential gates

• to empower LSTMs ability to revise storage decisions
• with normalization and stabilization
• Input & Forget gates can have exponential activation functions

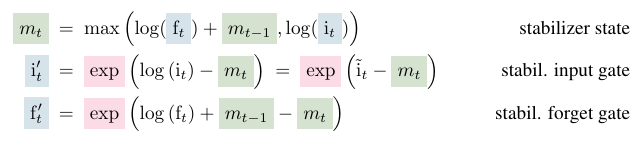
Normalizing exponential gates

• Exponential gating can lead to overflow
• Use normalizer state $m_t$
  • sums up the product of input gate times all future forget gates (?)
• Using $\textmd{f}'$ and $\textmd{i}'$ does not change the output of the whole network, nor changing the derivatives of the loss

New Memory Mixing

• Multiple memory cells like the original LSTM
• Multiple memory cells enable memory mixing via recurrent connections $R$ from hidden state vector $h$ to memory cell input $z$ and the gates $\textmd{i, f, o}$
• Can have multiple heads with memory mixing within each head (not across heads)

2.3 mLSTM

• LSTM memory cell ($c \in \mathbb{R}$) to a matrix $C \in \mathbb{R}^{n\times n}$ -> enhance storage capacity
• retrieval is performed via a matrix multiplication

Covariance update rule

• Store key $k_t\in\mathbb{R}^d$ and value $v_t\in\mathbb{R}^d$ at time $t$
• Value $v_t$ should be retrieved by a query vector $q_{t+\tau}\in\mathbb{R}^d$ at time $t+\tau$
• Covariance update rule for storing a key-value pair
  • $C_t=C_{t-1}+v_tk_t^\top$
• key & value -> zero mean due to layer-norm
• Covariance update rule is optimal for maximal separability of retrieved binary vectors (maximal signal/noise ratio)
• Forget gate corresponds to decay rate and the input gate to the learning rate of Fast Weight Programmers

normalizer state

• weighted sum of key vectors
• key vector weighted by the input gate and all future forget gates
• Use absolute value of dot product of query and normalizer state, lower bound it by a threshold (following Retentive network)

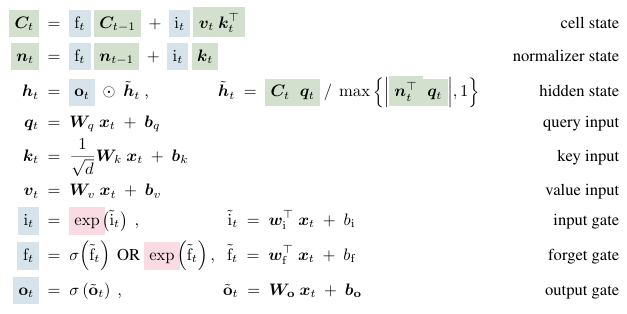
• Multiple memory cells with multiple heads and multiple cells (no memory mixing)
• Same exponential gate with same stabilization techniques
• No memory mixing -> parallelizable!

2.4 xLSTM Architecture

xLSTM Blocks

• The block should non-linearly summarize the past in high-dimensional space to better separate contexts
• Seperating history -> prerequisite to correct prediction of next sequence element.

Cover's Theorem

• In a higher dimensional space non-linearly embedded patterns can more likely be linearly separated than in the original space.

Residual blocks

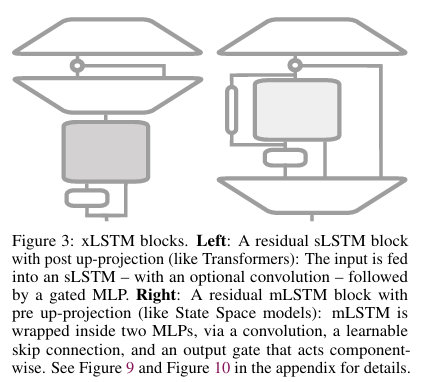
1. Residual block with post up-projection (like Transformers - left)

• non-linearly summarizes the past in the original space
  -> linearly maps into a high-dim space
  -> apply non-linear activation function
  -> linearly maps back to the original space
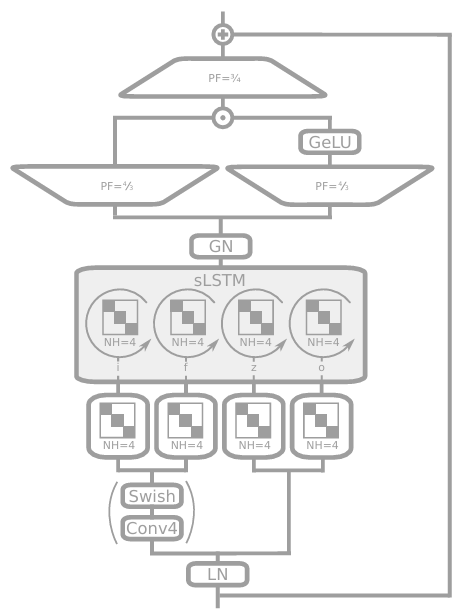
  => For xLSTM block with sLSTM

2. Residual block with pre up-projection(like SSMs - right)

• linearly maps to a high-dim space
  -> non-linearly summarizes the past in the high-dim space
• linearly maps back to the original space

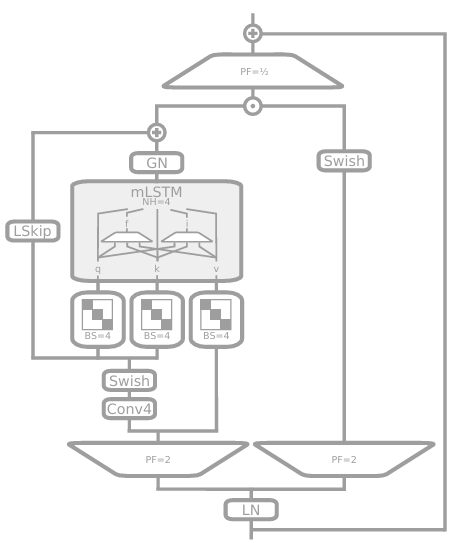
=> For xLSTM block with mLSTM (memory capacity issue)

sLSTM diagram

mLSTM diagram

xLSTM Architecture

• residually stacking building blocks
• pre-LayerNorm(most common)

2.5 Memory and Speed Considerations

Linear

• Linear computation and a constant memory complexity to seq length
• Compressive memory

trade-off

• memory of mLSTM does not require parameters, but computationally expensive ($d\times d$ matrix memory & $d\times d$ update)
• trade off memory capacity against computational complexity
• Parallel computation with GPU -> minor effect

CUDA for sLSTM

• Not parallelizable due to memory mixing
• CUDA implementation with GPU memory optimizations to the register level
• less than 2 times slower than mLSTM

3 Related Work

Linear Attention

• Synthesizer(learns synthetic attention)
• Linformer(self-attention by low-rank matrix)
• Linear Transformer(linearizes attention mechanism)
• Performer(approximate attention with positive orthogonal random feature)
• SGConv (replace attention by fast long convolution)

State Space Models

• linear in context length
• S4, DSS, GSS, S5, BiGS, H3, Mamba

Recurrent Neural Networks

• recent development of RNN in LLMs
• LRUs(RNNs with Deep Linear Recurrent Units)
• Hierarchically Gated Linear RNN(HGRN, HGRN2)
• RWKV

Gating

• Key ideas of LSTM
• Rediscovered and reinterpreted by
  • HGRN, HGRN2, Gated Linear Attention, Gated State Space models, Bidirectional Gated SSM, Moving Average Equipped Gated Attention, RWKV, Mamba

Covariance Update Rule

• mLSTM cell with covariance update rule
• Fast Weight Programmers, RWKV-5, RWKV-6, Retention, Linear Transformer, HGRN2

Most Related

• Closest model: Rentention, RWKV, HGRN2
• Matrix memory & gating
• No memory mixing
  • Memory mixing enables to solve state tracking problems => more expressive than SSMs and Transformers

Residually Stacking Architectures

• Almost all contemporary large deep learning models
• deep convolution networks and Transformers
  
  (??)

4 Experiments

Evaluation with a focus on language modeling

• 4.1 specific capability on synthetic tasks
• 4.2 validation set perplexity (trained on 15B SlimPajama)
• 4.3 thorough language modeling experiment (300B SlimPajama)

Notation

• xLSTM[$a$:$b$] -> ratio $a/b$ of mLSTM verses sLSTM
  • xLSTM[7:1]: 7 are mLSTM-based blocks, one is an sLSTM-based block out of eight blocks
• Common total block number: 48

4.1 Synthetic Tasks and Long Range Arena

Test of xLSTM's Exponential Gating with Memory Mixing

• Solve the state tracking problems
  

• Compare 2-block architectures

  • xLSTM[0:1], xLSTM[1:0], xLSTM[1:1], Llama, Mamba, RWKV, Rentention, Hyena, LSTM, LSTM in Transformer Blocks

• Architectures without memory mixing (no state tracking) cannot solve e.g. regular grammars like the parity task
  

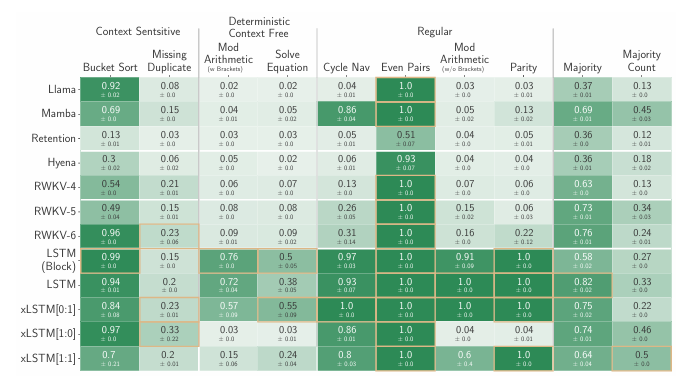
• Agreement with findings that Transformers and State Space models are fundamentally less powerful than RNNs

Test of xLSTM's Memory Capacities on Associative Recall Tasks

• Multi-Query Associative Recall task
• For each sequence, key-value pairs are randomly chosen from a large vocabulary, which must be memorized for later retrieval
• Enhanced difficulty of tasks (256 key-value pairs, 2048 context length)

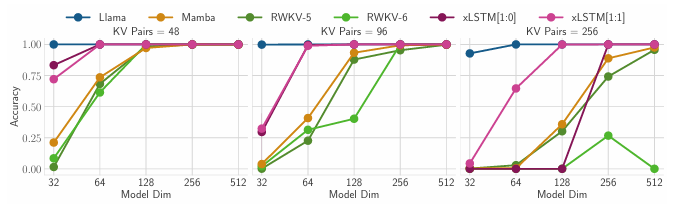
• Transformers -> gold standard at this task (exponential coding dimension memory)
• xLSTM is the best among non-Transformer models

Test of xLSTM's Long Context Capabilities on Long Range Arena

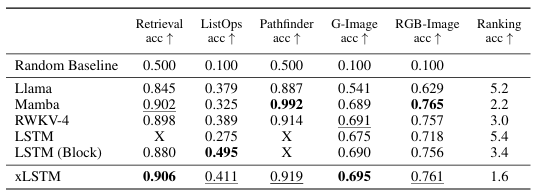
• consistent strong performance on all of the tasks

4.2 Method Comparison and Ablation Study

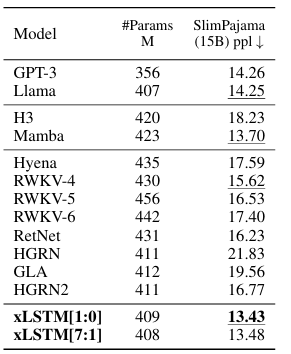
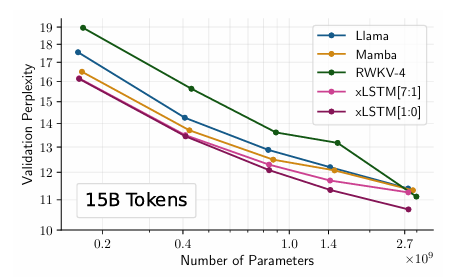
Comparing xLSTM to Other Methods

• Train models on 15B tokens from SlimPajama
• Evaluate perplexity
• embedding dim 1024 and 24 residual blocks

Ablation Studies

• Morph a vanilla xLSTM architecture step-by-step into xLSTM architecture

1. pre-LayerNorm residual backbones for LSTM
2. post up-projection block
3. exponential gating
4. matrix memory

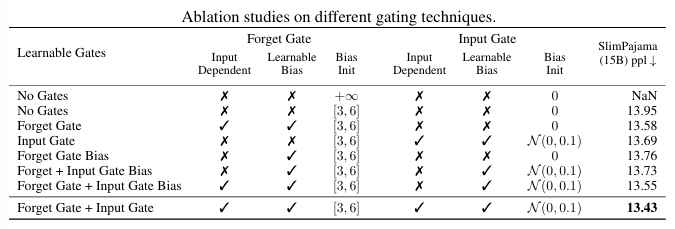
Different gating techniques

• changing learablity of gates
  

4.3 xLSTM as Large Language Model

• 300B token training from SlimPajama
• Same with Mamba, Griffin
• PALOMA benchmark

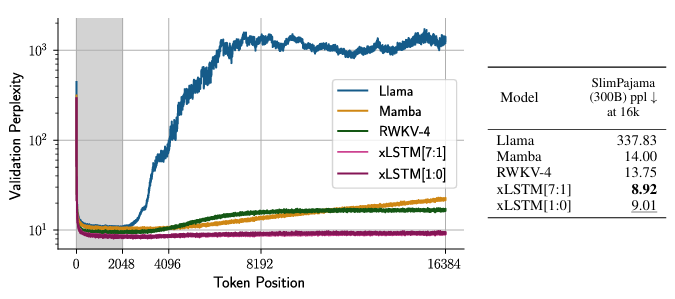
Sequence Length Extrapolation

• sequence length extrapolation on 1.3B-sized models
• train on 2048, tested up to 16384
  

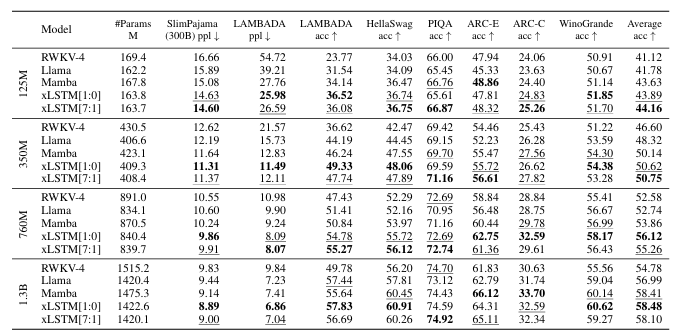
Validation Perplexity and Downstream Tasks

• Evaluate next token prediction & downstream tasks
• xLSTM wins in vast majority (ARC task, Mamba performed)
  

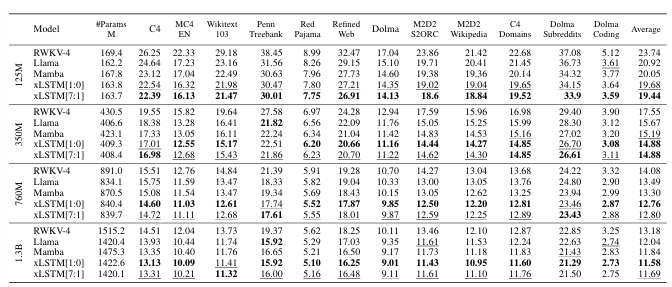
Performance on PALOMA Language Tasks

• xLSTM[1:0] performs better than xLSTM[7:1] on these language tasks.
  

• win on perplexity

  • vs Mamba (568/571)
  • vs Llama (486/571)
  • vs RWKV-4 (570/571)

Scaling Laws

• Scaling will continue..?
  

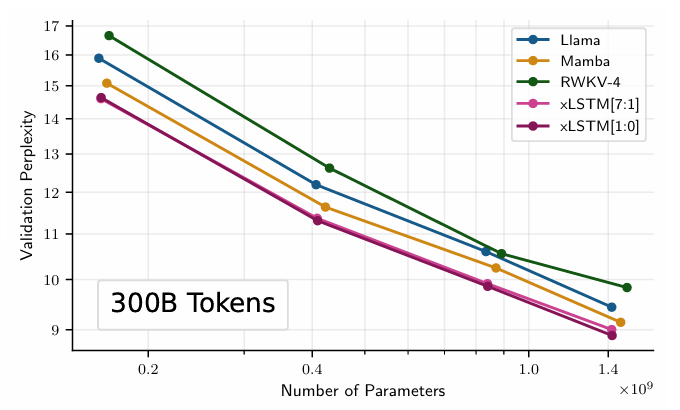
5 Limitations

1. non-parallel sLSTM

• Memory mixing prohibits parallelizable operations
• Developed CUDA kernels for sLSTM (around 1.5 times slower than parallel mLSTM implementation)

2. Non-optimized mLSTM

• CUDA kernels for mLSTM are not optimized
• 4 times slower than FlashAttention or selective scan in Mamba
• Can be optimized like flashattention(?)

3. High computation complexity of mLSTM matrix memory

• $d\times d$ matrices must be processed
• but minor
  • no parameter of memory update and retrieval
  • parallezied using standard matrix operation

4. Forget Gates Initialization

• Must be chosen carefully

5. Possible Overload of Memory

• matrix memory: indenpendant of the sequence length
• longer context -> might overload the memory
• Not limited up to 16k

6. lack of optimization

• expensive computational load for large language experiments
• not fully optimized -> extensive optimization needed for full potential

6 Conclusion

• Partly answered the question "How far do we get in language modeling when scaling LSTM to billions of parameters?"
• Answer: "At least as far as current technologies like Transformers or State Space Models"
• Scaling laws -> xLSTM models will be serious competitors to current LLM

Appendix

Parallel mLSTM Forward Pass

• Processes all times steps of a full sequence $X \in \mathbb{R}^{T\times d}$ at once ($T$ is seq length, $d$ is head dimension)
• Shows for single head dimension

Steps

• $\tilde{\textmd{f}} \in \mathbb{R}^T$: forget gate pre-activations

• $\tilde{\textmd{i}} \in \mathbb{R}^T$: input gate pre-activations

• $\textmd{F}\in \mathbb{R}^{T\times T}$: forget gate activation matrix

  • $F_{ij} = \begin{cases} 0 & \text{for } j>i\\ 1 & \text{for } j=i\\ \prod^{i}_{k=j+1} \sigma(\tilde{\text{f}}_k) & \text{for } j<i \end{cases}$

• $\tilde{\textmd{I}}\in \mathbb{R}^{T\times T}$: input gate pre-activation matrix

  • $\tilde{\textmd{I}}_{ij}=\begin{cases} 0 & \text{for } j>i\\ i_j &\text{for } i\geq j\end{cases}$

• $\textmd{D} \in R^{T\times T}$: unstabilized gate activation matrix

  • $\textmd{D}=\textmd{F}\odot\exp(\tilde{\textmd{I}})$

• $\textmd{D}' \in R^{T\times T}$: stable gate activation matrix

  • avoid overflow due to the exponential function
  • $\tilde{\textmd{D}}=\log\textmd{D}=\log(\textmd{F}\odot\exp(\tilde{\textmd{I}}))=\log\textmd{F}+\tilde{\textmd{I}}$
  • $\textmd{D}'=\exp(\tilde{\textmd{D}}-\max\tilde{\textmd{D}})$

• $\tilde{\textmd{H}} \in\mathbb{R}^{T\times d}$: all hidden pre-activation states

  • Given queries, keys and values $Q,K, V\in \mathbb{R}^{T\times d}$

  • Un-stabilized version

  • $\tilde{\textmd{H}}=CV$

    • $C=\tilde{C}/\max(|\sum^T_{j=1}\tilde{C}_{i,j}|, 1)$
    • $\tilde{C}={{QK^\top}\over{\sqrt{d}}}\odot \textmd{D}$

  • Stablized version

  • $\tilde{\textmd{H}}=CV$

    • $C=\tilde{C}'/\max(|\sum^T_{j=1}\tilde{C}_{i,j}'|, \exp(-\max\tilde{\textmd{D}}))$
    • $\tilde{C}'={{QK^\top}\over{\sqrt{d}}}\odot \textmd{D}'$

• $\tilde{\textmd{O}}\in \mathbb{R}^{T\times d}$: output gate pre-activations

• $H\in\mathbb{R}^{T\times d}$: hidden states for all timesteps

  • $\textmd{H}=\sigma(\tilde{\textmd{O}})\odot\tilde{\textmd{H}}$