Cross Validation
a process of resampling machine learning model in a limited data sample
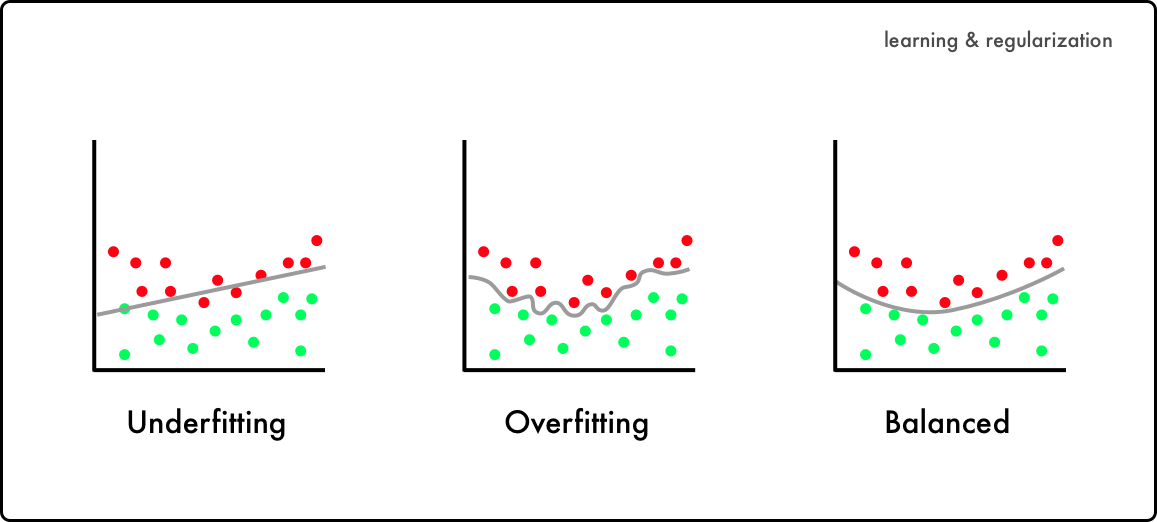
From the previous post, we learned the importance of splitting data-set into train and test sets. However, such technique is still vulnerable to "overfitting" : production of an analysis that corresponds too closely or exactly to a particular set of data.
We may first think that it is perfectly preferable to have "too close or exact" correspondence to a set of data. Nevertheless, overfitting is likely to undermine the performance of the model when performing prediction in completely different dataset.
Hence, cross-validation is introduced to avoid any imbalance in data, and to extract better evaluation metrics.
K-Fold Cross Validation
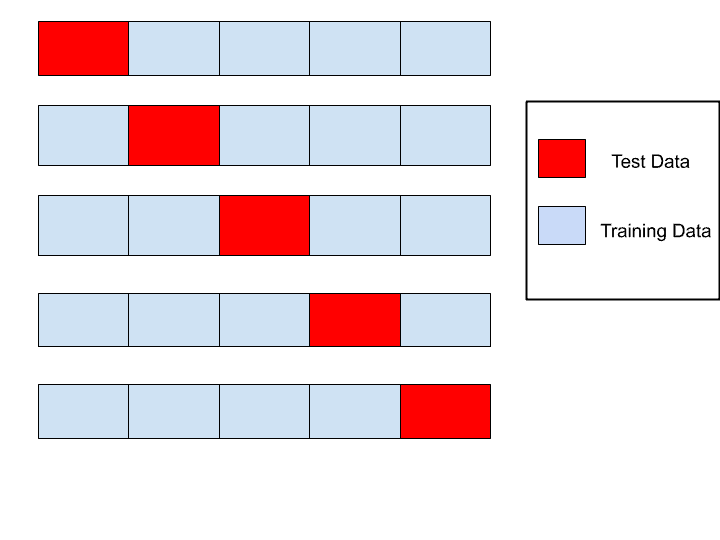
In K-Fold cross validation, we will be splitting the data "k-times" and return the mean of accuracy for each k-th training.
First, let us import modules to perform k-fold cross validation on iris dataset.
import sklearn
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import KFold
import numpy as np
iris = load_iris()
features = iris.data
label = iris.target
dt_clf = DecisionTreeClassifier(random_state=156)
# create KFold object & list to contain each accuracy results
kfold = KFold(n_splits=5)
cv_accuracy = []
print('Size of Dataset : ', features.shape[0])
Output
Size of Dataset : 150Since we created total of five KFold object, 120 data set will be classified as train dataset while 30 will be test dataset.
n_iter = 0
# KFold split() returns index of train and test sets
for train_index, test_index in kfold.split(features):
# extract data by using indice
X_train, X_test = features[train_index], features[test_index]
y_train, y_test = label[train_index], label[test_index]
# train & predict
dt_clf.fit(X_train, y_train)
pred = dt_clf.predict(X_test)
n_iter = n_iter + 1
# estimate accuracy after each iteration
accuracy = np.round(accuracy_score(y_test, pred), 4)
train_size = X_train.shape[0]
test_size = X_test.shape[0]
print('#{0} \n Cross Validation Accuracy : {1}, Size of Train Data {2}, Size of Test Data {3}'
.format(n_iter, accuracy, train_size, test_size))
print('#{0} \n Index of Test Set : {1} : \n'
.format(n_iter, test_index))
cv_accuracy.append(accuracy)
print('Mean Accuracy : ', np.mean(cv_accuracy))
Output
#1
Cross Validation Accuracy : 1.0, Size of Train Data 120, Size of Test Data 30
#1
Index of Test Set : [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29] :
#2
Cross Validation Accuracy : 0.9667, Size of Train Data 120, Size of Test Data 30
#2
Index of Test Set : [30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
54 55 56 57 58 59] :
#3
Cross Validation Accuracy : 0.8667, Size of Train Data 120, Size of Test Data 30
#3
Index of Test Set : [60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83
84 85 86 87 88 89] :
#4
Cross Validation Accuracy : 0.9333, Size of Train Data 120, Size of Test Data 30
#4
Index of Test Set : [ 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107
108 109 110 111 112 113 114 115 116 117 118 119] :
#5
Cross Validation Accuracy : 0.7333, Size of Train Data 120, Size of Test Data 30
#5
Index of Test Set : [120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137
138 139 140 141 142 143 144 145 146 147 148 149] :
Mean Accuracy : 0.9
The mean average of 5-fold cross validation is 90%. We can see that the indice of test-set differ for each k-th step of cross validation.
Stratified K-Fold
Imagine a set of data with imbalanced label data distribution.
For example, imagine we are training a model to detect spam mails. Assume that out of 100,000,000 mails there exist 1,000 spam mails. Total number of spam mails occupies a very small portion of total dataset (0.0001%), hence distorting the training model due to its imbalanced distribution.
Stratified K-Fold solves this problem by considering the distribution of the original dataset and distributing identical label data for each fold of cross validation.
Let us first check the distribution of label data from iris sample.
# stratified KFold
import pandas as pd
iris = load_iris()
iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
iris_df['Label'] = iris.target
iris_df['Label'].value_counts()Output
2 50
1 50
0 50We will now create an imbalanced dataset and check the distribution.
kfold = KFold(n_splits=3)
n_iter = 0
for train_index, test_index in kfold.split(iris_df):
n_iter = n_iter + 1
label_train = iris_df['Label'].iloc[train_index]
lebel_test = iris_df['Label'].iloc[test_index]
print('## Cross Validation {0}'.format(n_iter))
print('\n Train Index : \n {0}'.format(label_train.value_counts()))
print('Test Index : \n {0} \n'.format(lebel_test.value_counts()))Ouput
## Cross Validation 1
Train Index :
2 50
1 50
Name: Label, dtype: int64
Test Index :
0 50
Name: Label, dtype: int64
## Cross Validation 2
Train Index :
2 50
0 50
Name: Label, dtype: int64
Test Index :
1 50
Name: Label, dtype: int64
## Cross Validation 3
Train Index :
1 50
0 50
Name: Label, dtype: int64
Test Index :
2 50
Name: Label, dtype: int64 For Cross Validation 1 , fifty indice were selected for label data 1 and 2, while fifty indice of 0 were selected for test data. This is problematic since the model will not be able to train case-0 in any case.
Now let us solve this by implementing stratified K-fold.
from sklearn.model_selection import StratifiedKFold
skf = StratifiedKFold(n_splits=3)
n_iter = 0
for train_index, test_index in skf.split(iris_df, iris_df['Label']):
label_train = iris_df['Label'].iloc[train_index]
label_test = iris_df['Label'].iloc[test_index]
print('### Cross Validation {0}'.format(n_iter))
print('Train Index : \n', label_train.value_counts())
print('Test Index : \n', label_test.value_counts())Output
### Cross Validation 0
Train Index :
2 33
1 33
0 33
Name: Label, dtype: int64
Test Index :
2 17
1 17
0 17
Name: Label, dtype: int64
### Cross Validation 0
Train Index :
2 33
1 33
0 33
Name: Label, dtype: int64
Test Index :
2 17
1 17
0 17
Name: Label, dtype: int64
### Cross Validation 0
Train Index :
2 34
1 34
0 34
Name: Label, dtype: int64
Test Index :
2 16
1 16
0 16
Name: Label, dtype: int64Accuracy Using Stratified K-fold
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
import numpy as np
dt_clf = DecisionTreeClassifier(random_state=156)
skfold = StratifiedKFold(n_splits=3)
n_iter = 0
cv_accuracy = []
for train_index, test_index in skfold.split(features, label):
X_train, X_test = features[train_index], features[test_index]
y_train, y_test = label[train_index], label[test_index]
dt_clf.fit(X_train, y_train)
pred = dt_clf.predict(X_test)
accuracy = np.round(accuracy_score(y_test, pred), 4)
cv_accuracy.append(accuracy)
n_iter = n_iter + 1
train_size = X_train.shape[0]
test_size = X_test.shape[0]
print('#{0} Cross Validation Accuracy : {1}, Train Data Size : {2}, Test Data Size : {3}'
.format(n_iter, accuracy, train_size, test_size))
print('Accuracy by Index : ', cv_accuracy)
print('Average Accuracy : ', np.mean(cv_accuracy))Output
#1 Cross Validation Accuracy : 0.9804, Train Data Size : 99, Test Data Size : 51
#2 Cross Validation Accuracy : 0.9216, Train Data Size : 99, Test Data Size : 51
#3 Cross Validation Accuracy : 0.9792, Train Data Size : 102, Test Data Size : 48
Accuracy by Index : [0.9804, 0.9216, 0.9792]
Average Accuracy : 0.9604Cross Val Score
cross_val_score() API easily returns a metrics after automatically cross validating and stratifiying the dataset if needed.
Parameters of Cross Val Score
cross_val_score(estimator, X, y=None, scoring=None, cv=None, n_jobs=1, verbose=0, fit_params=None, pre_dispatch='2*n_job')estimator, X, y, scoring & cv are the main parameters
# cross_val_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score, cross_validate
from sklearn.datasets import load_iris
import numpy as np
iris_data = load_iris()
dt_clf = DecisionTreeClassifier(random_state=156)
data = iris_data.data
label = iris_data.target
# evaluation metrics is accuracy, fold to total 3 splits
scores = cross_val_score(dt_clf, data, label, scoring='accuracy', cv=3)
print('Accuracy for Each Index : ', np.round(scores, 4))
print('Average Accuracy : ', np.round(np.mean(scores), 4))Output
Accuracy for Each Index : [0.9804 0.9216 0.9792]
Average Accuracy : 0.9604

It's evident that the authors have a deep understanding of the subject matter and are passionate about helping readers make informed decisions. browse this site check here original site my response pop over to these guys