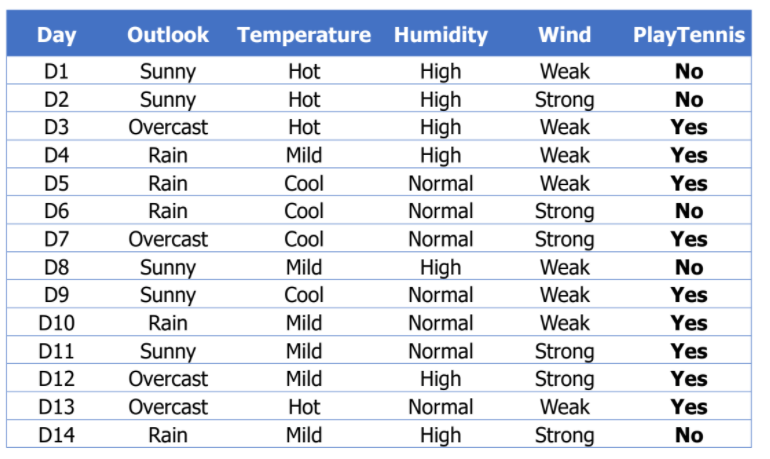
- 만약,
Outlook: Overcast, Temperature: Hot, Humidity: Normal, Wind: Weak일 때,
PlayTennis: Yes? No?
Intro
Classificationby Partitioning Example Space- 목표 : 이산적인 값을 가진 target functions의 근사치 구하기
- Examples은 attribute-value 쌍으로 주어짐
- target function은 discrete output value를 가짐
- training data는 missing (특정 값이 비어있는) attribute values 값을 포함할 수 있음
Example Space
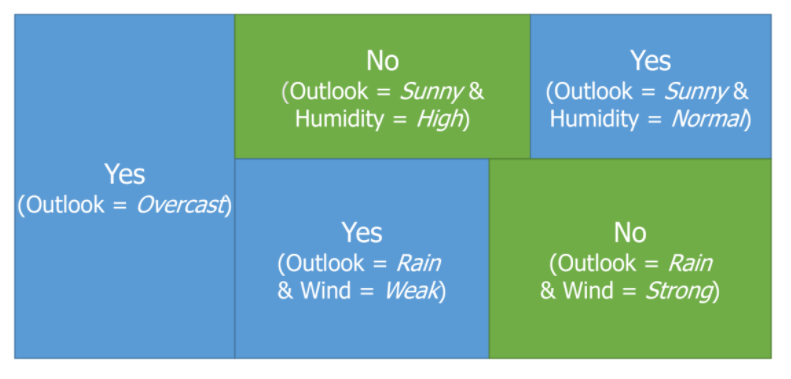
Decision tree
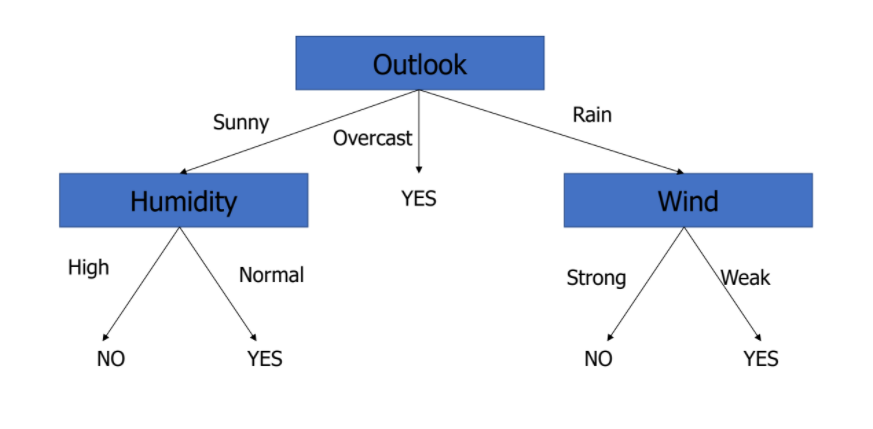
- Data 학습 ⇒ model을 만드는 것! 즉 이런 tree를 만드는 것 ❗
💡 그렇다면 어떤 attribute를 root로 올리는 게 가장 적합할까?
📌 주어진 data를 가장 유용하게 분류할 수 있는 attribute
-
Quantitative measure, 측정할 수 있는 measure -
Information Gain
-
Attribute A는 data D에 상대적
-
값이 가장 높은 attribute를 root node로 선택
-
: 원래 주어진 Entropy
-
: Attribute A를 선택했을 때의 Entropy 변화
Entropy
-
Impurityof an arbitrary collection of examples -
불확실성
-
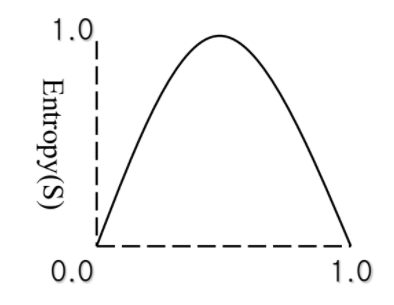
는 확률 값
-
value가 Yes/No 있을 때, 모두 Yes거나 No이면Entropy(불확실성)는 0
Example: Play Tennis
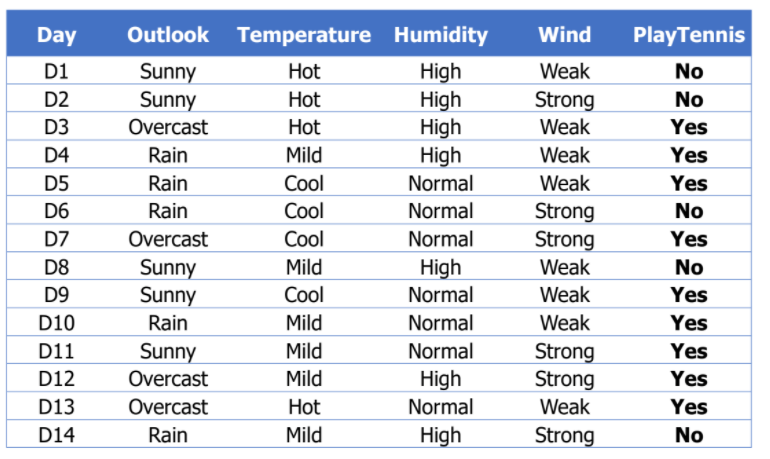
Entropy of D
- = [9+, 5-]
- 14개의 data 중 Yes 9개, No 5개
📌 Attribute Wind
- = [6+, 2-]
- = [3+, 3-]

📌 Attribute Humidity
- = [3+, 4-]
- = [6+, 1-]

- 남은 attiribute도 같은 방식으로 계산
💡 Best Attribute?
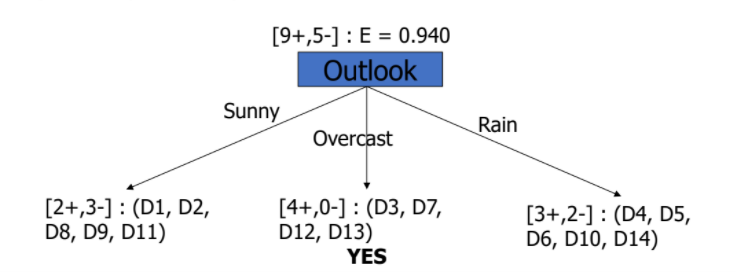
- Gain(D, Outlook) = 0.246
- Gain(D, Humidity) = 0.151
- Gain(D, Wind) = 0.048
- Gain(D, Temperature) = 0.029
Entropy D_sunny
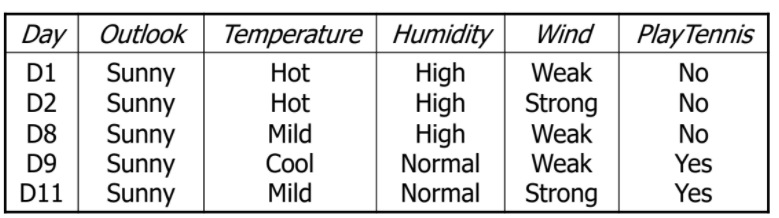
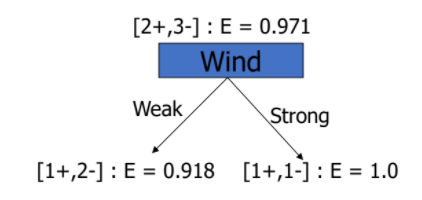
📌 Attribute Wind
- = [1+, 2-]
- = [1+, 1-]
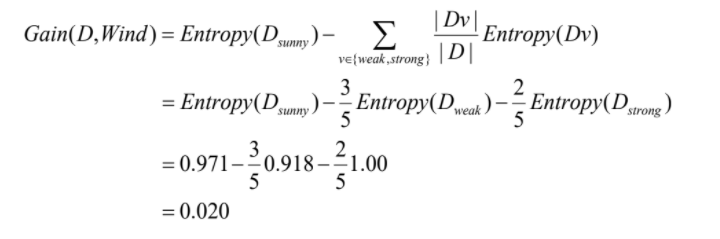
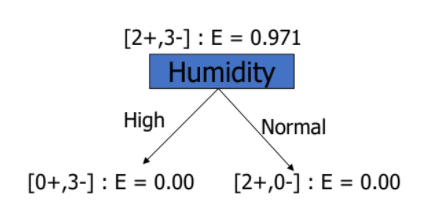
📌 Attribute Humidity
- = [0+, 3-]
- = [2+, 0-]
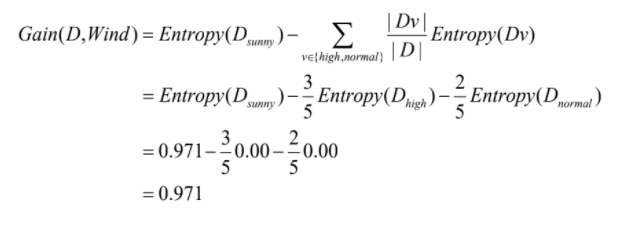
- 남은 attiribute도 같은 방식으로 계산
💡 Best Attribute?
- Gain(D, Humidity) = 0.971
- Gain(D, Wind) = 0.020
- Gain(D, Temperature) = 0.571
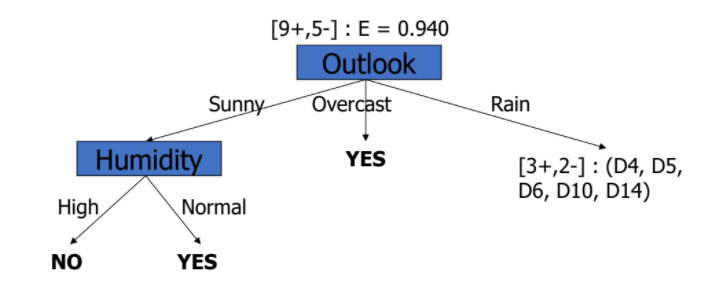
Entropy D_rain
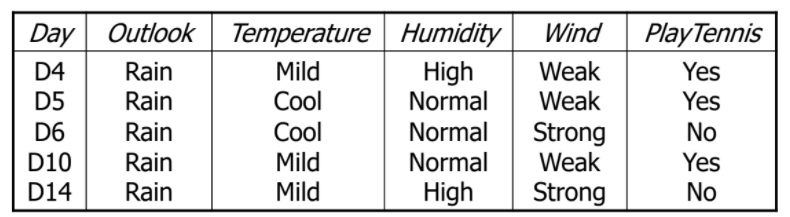
📌 Attribute Wind
- = [3+, 0-]
- = [0+, 2-]
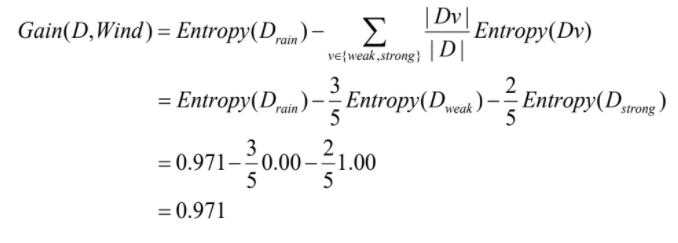
- 위에 이 아니라 임..!
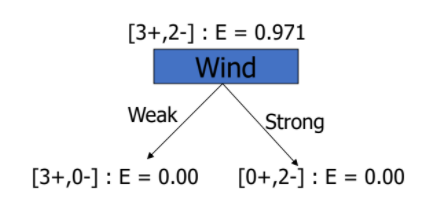
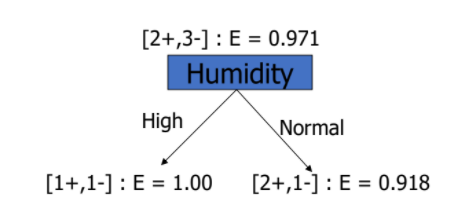
📌 Attribute Humidity
- = [1+, 1-]
- = [2+, 1-]
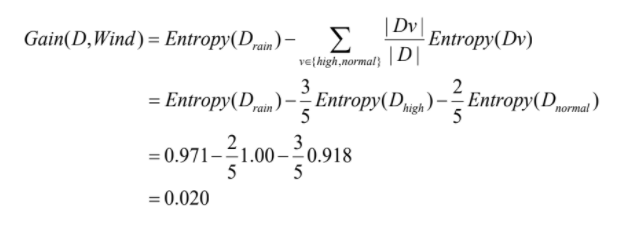
- 남은 attiribute도 같은 방식으로 계산
💡 Best Attribute?
- Gain(D, Humidity) = 0.020
- Gain(D, Wind) = 0.971
- Gain(D, Temperature) = 0.020
최종
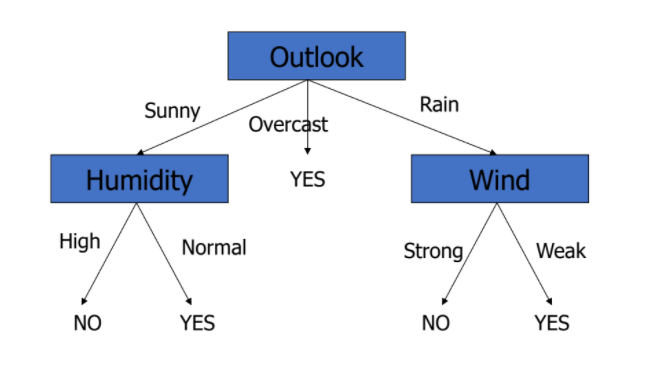
-
만약,
Outlook: Overcast, Temperature: Hot, Humidity: Normal, Wind: Weak일 때,
PlayTennis: Yes!! -
직관적으로 설명 가능 (if-then으로 모델 설명 가능)
-
계산 과정이 굉장히 복잡하고 어려워보이지만 실제로 해보면 귀찮아서 그렇지 못할 짓도 아님.. 한번쯤은 따라 해보는 거 추천 👍
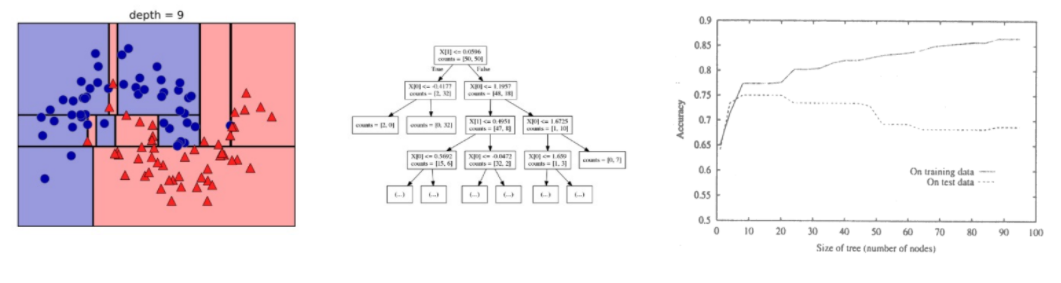
Overfitting
-
tree depth가 깊어지는 것
-
방지
- 성능이 줄어들지 않는 한 가지치기 (validation data를 보고)
- 미리 depth 제약 두기