- Linear regression을 통해 얻은 data 및 최적의 linear 가설 공간
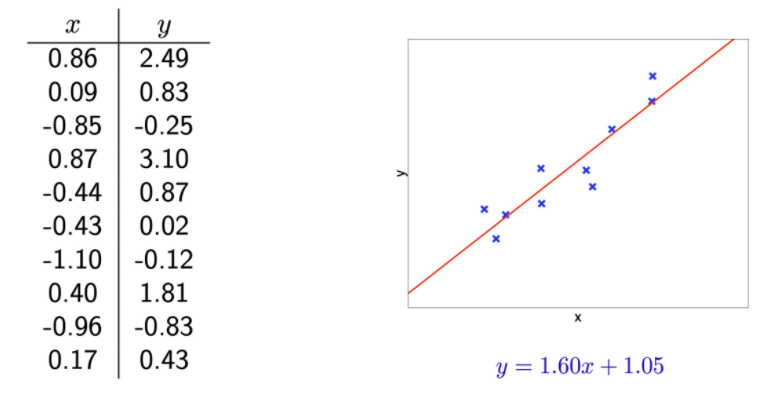
1.60,1.05는 각각 으로 1차원의 가설 공간!
💡 그렇다면 linear regression으로 충분할까?
- Linear regression은 대부분의 현실 문제에 비해 너무 심플함
- 하지만, real-valued outputs을 위해 가장 먼저 시도하는 방법
2가지 해결 방법
1. Transform the data
- Add cross-terms, higher-order terms
- X에서 다른 공간 X'로 입력 transformation을 적용한 다음, 변환된 공간에 선형 회귀 수행
2. Use a different hypothesis class (e.g. non-linear functions)
- 주어진 문제를 linear하게 표현하지않고, 다항식으로 표현 ❗
⇒
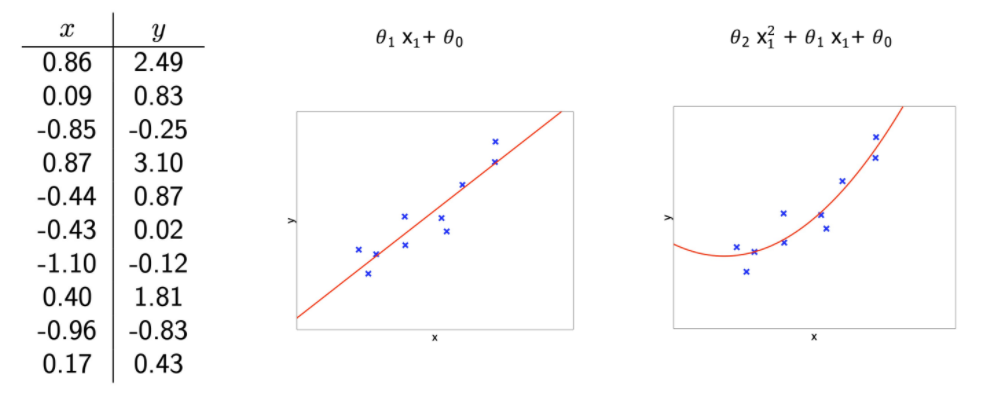
다항 회귀
-
Polynomial regression -
데이터에 고차원의 다항식을 적용
E.g., -
즉, x와 y 사이의 관계는 x에서 n차 다항식으로 모델링
-
이 주어짐
-
우리는 d+1개의 파라미터(θ)가 필요
💡 Data에 가장 적합한 fit은 무엇일까? Order-9 fit이 가장 좋은걸까?
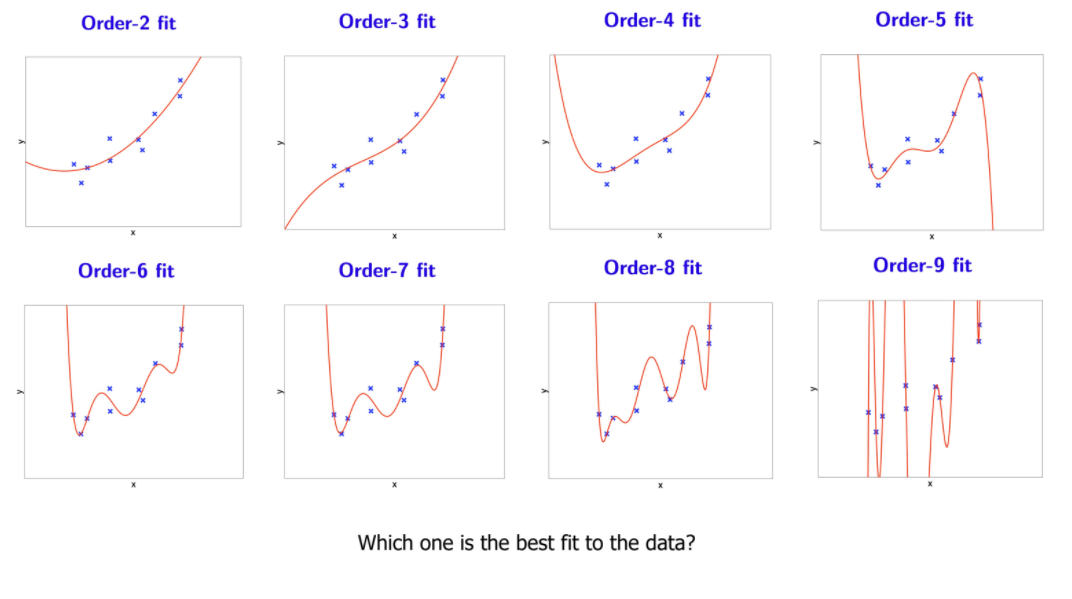
Order-9 fit
- 새로운 data에 대해서는 부적절!
- 과적합!!
Overfitting (과적합)
-
기계 학습(machine learning)에서 학습 데이터를 과하게 학습(overfitting)하는 것
-
모든 머신 러닝 알고리즘에서 매우 중요한 문제 ❗
-
우리는 training data는 완벽하게 예측하지만, 새로운 data로는 잘 일반화되지 않는 함수 (hypothesis)를 찾을 수 있음
ex) 위에서 본 order-9 fit -
기계 학습의 핵심은
training data로부터model을 학습하고, 그 model을 바탕으로Unseen data즉,test data를 예측하는 것 -
만약, 파라미터의 수가 많다면 모든 data points를 기억(memorizes)하지만, 다른 모든 곳에서는 wild!!
📌 Another overfitting example
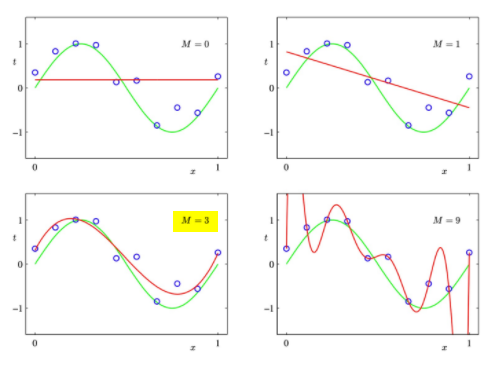
- 다항식 M의
degree가 높을수록, 자유도가 높아지고, training data를 과적합(overfitting)할 수 있는 capacity도 높아짐! - M = 3이 가장 적합
📌 Typical overfitting plot
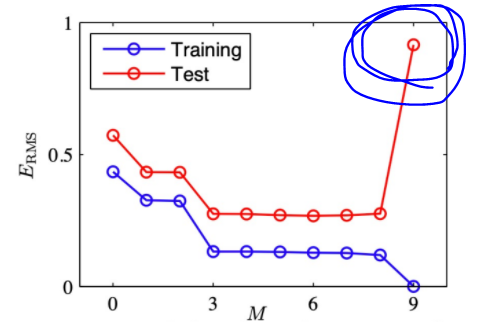
- triaing error는 다항식 M의 degree, 즉 가설의 복잡성에 따라 감소
💡 참고
딥러닝에서는 다름! 데이터가 많아도 너무 많고, 모델 사이즈를 키워도 성능 좋아짐!
Prevent overfitting
💡 그럼 overfitting이 발생했다는 걸 어떻게 알고 예방할 수 있을까?
1. Cross-validation (다음 챕터)
2. Lager data
- 데이터 많이 수집하기!!
- Dataset이 작을수록,
empirical loss(경험적 손실?)과expected loss(기대 손실)의 차이가 커짐 - self-supervised learning : 정답이 있는데 label을 스스로 만듦
⇒ data를 엄청나게 만들 수 있음!
3. 쓸데없는 가설(hypotheses) 버리기
4. Regularization (정규화)
- hypotheses(가설)을 제한하는 몇 가지 주요 방법
- 기타 유형의 정규화 :
Data augmentation,Early stopping, ...
Regularization
-
일반적으로 과적합을 방지하거나 최적화에 도움이 되는 방법
-
특히 최적화를 돕거나 과적합을 방지하기 위해 training optimization objective에 additional terms (추가 항 사용)
⇒Shrinkagein statics -
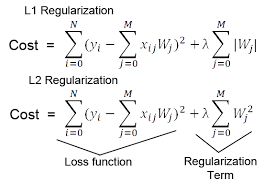
Idea: 비용 함수(cost function)를 변경하여 가설(hypothesis)의 복잡성에 패널티 부여 -
: cost function
: 정답 값 (label)
: 예측한 값 -
λ: 제약 조건
클수록 전체가 작아짐! -
: Regularization term
-
를 minimalize하려고 하면 memorize하게 됨! 때문에
Regularization term을 두고 있음
Regression with regulation
📌 Norm
- 벡터의 길이 혹은 크기를 측정하는 방법(함수)
- 단어나 기사와 같은 것들을 벡터로 표현해서 비슷한 것들은 거리를 최소화하고, 비슷하지 않은 것들은 거리를 최대화할 때
norm의 개념이 활용 Lp norm
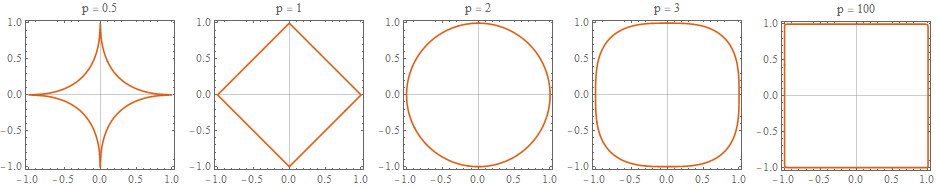
출처 : https://ekamperi.github.io/machine%20learning/2019/10/19/norms-in-machine-learning.html
-
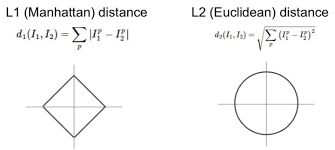
L1 norm
: 벡터의 요소에 대한 절댓값의 합, Manhattan norm
-
L2 norm
: 각 원소들의 제곱의 합을 제곱근으로 이상치에 민감, Euclidean norm
📌 Lasso regression ⇐ L1 regularization
L1 loss에regulartization term을 붙인 것- 의미 없는 feature에
L1 regularization을 사용하면 해당 feature의 weight를 0으로 만듦
📌 Ridge regression ⇐ L2 regularization
L2 loss에regulartization term을 붙인 것Lasso regression과 다르게 불필요한 feature의 weight를 0에 가깝게 만들 뿐, 0으로 만들진 않음
- 값에 따라 정규화로 과적합을 피할 수 있음, 작을수록 약한 정규화
- 를 어떻게 정해? ⇒
cross-validation
⭐ 출처
https://sooho-kim.tistory.com/85
https://junklee.tistory.com/29
