2.2 벡터와 행렬의 연산

벡터/행렬의 덧셈과 뺄셈

같은 크기를 가진 두 개의 벡터나 행렬은 덧셈과 뺄셈을 할 수 있다. 두 벡터와 행렬에서 같은 위치에 있는 원소끼리 덧셈과 뺄셈을 하면 된다. 이러한 연산을 요소별(element-wise) 연산이라고 한다.

예를 들어 벡터 $x$와 $y$가 다음과 같으면,

벡터 $x$와 $y$의 덧셈 $x+y$와 뺄셈 $x-y$는 다음처럼 계산한다.

벡터의 덧셈과 뺄셈을 넘파이로 계산하면 다음과 같다. 여기에서는 편의상 1차원 배열로 벡터를 표시하였다.

x = np.array([10, 11, 12, 13, 14])
y = np.array([0, 1, 2, 3, 4])

x + y

array([10, 12, 14, 16, 18])

x - y

array([10, 10, 10, 10, 10])

행렬도 같은 방법으로 덧셈과 뺄셈을 할 수 있다.

np.array([[5, 6], [7, 8]]) + np.array([[10, 20], [30, 40]]) - 
np.array([[1, 2], [3, 4]])

array([[14, 24],
       [34, 44]])

스칼라와 벡터/행렬의 곱셈

벡터 $x$ 또는 행렬 $A$에 스칼라값 $c$를 곱하는 것은 벡터 $x$ 또는 행렬 $A$의 모든 원소에 스칼라값 $c$를 곱하는 것과 같다.

브로드캐스팅

원래 덧셈과 뺄셈은 크기(차원)가 같은 두 벡터에 대해서만 할 수 있다. 하지만 벡터와 스칼라의 경우에는 관례적으로 다음처럼 1-벡터를 사용하여 스칼라를 벡터로 변환한 연산을 허용한다. 이를 브로드캐스팅(broadcasting) 이라고 한다.

데이터 분석에서는 원래의 데이터 벡터 $x$가 아니라 그 데이터 벡터의 각 원소의 평균값을 뺀 평균제거(mean removed) 벡터 혹은 0-평균(zero-mean) 벡터를 사용하는 경우가 많다.

위 식에서 $m$은 샘플 평균이다.

선형조합

벡터/행렬에 다음처럼 스칼라값을 곱한 후 더하거나 뺀 것을 벡터/행렬의 선형조합(linear combination) 이라고 한다. 벡터나 행렬을 선형조합해도 크기는 변하지 않는다.

벡터나 행렬의 크기를 직사각형으로 표시하면 다음과 같다.

벡터와 벡터의 곱셈

행렬의 곱셈을 정의하기 전에 우선 두 벡터의 곱셈을 알아보자. 벡터를 곱셈하는 방법은 여러 가지가 있지만 여기서는 내적(inner product) 에 대해서만 다룬다. 벡터 $x$와 벡터 $y$의 내적은 다음처럼 표기한다.

내적은 다음처럼 점(dot)으로 표기하는 경우도 있어서 닷 프로덕트(dot product) 라고도 부르고 < $x,y$ > 기호로 나타낼 수도 있다.

두 벡터를 내적하려면 다음과 같은 조건이 만족되어야 한다.

1. 우선 두 벡터의 차원(길이)이 같아야 한다.

2. 앞의 벡터가 행 벡터이고 뒤의 벡터가 열 벡터여야 한다.

이때 내적의 결과는 스칼라값이 되며 다음처럼 계산한다. 우선 같은 위치에 있는 원소들을 요소별 곱셈처럼 곱한 다음, 그 값들을 다시 모두 더해서 하나의 스칼라값으로 만든다.

다음은 두 벡터의 내적의 예다.

넘파이에서 벡터와 행렬의 내적은 dot()이라는 명령 또는 @(at이라고 읽는다)이라는 연산자로 계산한다. 2차원 배열로 표시한 벡터를 내적했을 때는 결과값이 스칼라가 아닌 2차원 배열이다.

x = np.array([[1], [2], [3]])
y = np.array([[4], [5], [6]])

x.T @ y  # 또는 np.dot(x.T, y)

array([[32]])

넘파이에서는 1차원 배열끼리도 내적을 계산한다. 이때는 넘파이가 앞의 벡터는 행 벡터이고 뒤의 벡터는 열 벡터라고 가정한다.

x = np.array([1, 2, 3])
y = np.array([4, 5, 6])

x @ y  # 또는 np.dot(x, y)

32

왜 벡터의 내적은 덧셈이나 뺄셈과 달리 이렇게 복잡하게 정의된 것일까? 그 이유는 데이터 분석을 할 때 이러한 연산이 필요하기 때문이다. 벡터의 내적을 사용하여 데이터를 분석하는 몇 가지 예를 살펴보자.

가중합

벡터의 내적은 가중합을 계산할 때 쓰일 수 있다. 가중합(weighted sum) 이란 복수의 데이터를 단순히 합하는 것이 아니라 각각의 수에 어떤 가중치 값을 곱한 후 이 곱셈 결과들을 다시 합한 것을 말한다.

만약 데이터 벡터가 $x=[x_1, \cdots, x_N]^T$이고 가중치 벡터가 $w=[w_1, \cdots, w_N]^T$이면 데이터 벡터의 가중합은 다음과 같다.

이 값을 벡터 $x$와 $w$의 곱으로 나타내면 $w^Tx$ 또는 $x^Tw$ 라는 간단한 수식으로 표시할 수 있다.

예를 들어 쇼핑을 할 때 각 물건의 가격은 데이터 벡터, 각 물건의 수량은 가중치로 생각하여 내적을 구하면 총금액을 계산할 수 있다.

만약 가중치가 모두 1이면 일반적인 합(sum)을 계산한다.

또는

이면

연습 문제 2.2.1

A, B, C 세 회사의 주식은 각각 100만원, 80만원, 50만원이다. 이 주식을 각각 3주, 4주, 5주를 매수할 때 필요한 금액을 구하고자 한다.

(1) 주식의 가격과 수량을 각각 $p$ 벡터, $n$ 벡터로 표시하고 넘파이로 코딩한다.

(2) 주식을 매수할 때 필요한 금액을 곱셈으로 표시하고 넘파이 연산으로 그 값을 계산한다.

import numpy as np  # 넘파이 패키지 임포트
import matplotlib.pylab as plt  # 맷플롯립 패키지 임포트
p = np.array([100, 80, 50])
n = np.array([3, 4, 5])
print(p @ n) # 선형결합
print(p.T @ n)
print(p @ n.T)
print(p.T @ n.T)

가중평균

가중합의 가중치값을 전체 가중치값의 합으로 나누면 가중평균(weighted average) 이 된다. 가중평균은 대학교의 평균 성적 계산 등에 사용할 수 있다.

예를 들어 고등학교에서는 국어, 영어, 두 과목의 평균 점수를 구할 때 단순히 두 과목의 점수(숫자)를 더한 후 2으로 나눈다. 그러나 대학교에서는 중요한 과목과 중요하지 않는 과목을 구분하는 학점(credit)이라는 숫자가 있다. 일주일에 한 시간만 수업하는 과목은 1학점짜리 과목이고 일주일에 세 시간씩 수업하는 중요한 과목은 3학점짜리 과목이다. 1학점과 3학점 과목의 점수가 각각 100점, 60점이면 학점을 고려한 가중 평균(weighted average) 성적은 다음과 같이 계산한다.

벡터로 표현된 $N$개의 데이터의 단순 평균은 다음처럼 생각할 수 있다.

위 수식에서 보인 것처럼 $x$ 데이터의 평균은 보통 $\bar{x}$라는 기호로 표기하고 "엑스 바(x bar)" 라고 읽는다.

다음은 넘파이로 평균을 계산하는 방법이다.

x = np.arange(10)
N = len(x)

np.ones(N) @ x / N

4.5

현실적으로는 mean()이라는 메서드를 사용하는 것이 편하다.

x.mean()

4.5

연습 문제 2.2.2

벡터 $x$의 평균 제거 벡터는 다음과 같이 계산함을 증명하라.

$\mathbf{1}_N^Tx$는  $x$와 크기가 같은 일벡터와 $x$의 선형결합을 나타내고 이는 벡터  $x$의 모든 element의 합이 된다.

이를 $N$으로 나누면  $x$ 의 평균이 된다.

element-wise하게 이 스칼라값을 벡터 $x$에서 빼주기 위해

주어진 식은 벡터 $x$와 크기가 같은 컬럼 일벡터 $\mathbf{1}^{}_N$ 에 평균을 곱해서 얻은 벡터 $\mathbf{1}_N^Tx \mathbf{1}^{}_N$를 벡터 $x$에서 빼준 벡터이므로 벡터 $x$ 의 평균 제거 벡터라고 할 수 있다.

벡터 $x$의 평균을 $m$이라고 한다면, 모든 성분이 $m$인 벡터 $\mathbf{1}_N^Tx \mathbf{1}^{}_N$의 평균도 $m$이고 평균 연산은 뺄셈에 대해 분배법칙이 성립하므로 주어진 평균 제거 벡터의 평균은 0이 된다.

유사도

벡터의 곱셈(내적)은 두 벡터 간의 유사도를 계산하는 데도 이용할 수 있다. 유사도(similarity)는 두 벡터가 닮은 정도를 정량적으로 나타낸 값으로 두 벡터가 비슷한 경우에는 유사도가 커지고 비슷하지 앟은 경우에는 유사도가 작아진다. 내적을 이용하면 코사인 유사도(cosine similarity) 라는 유사도를 계산할 수 있다. 추후 선형대수의 기하학적 의미를 공부할 때 코사인 유사도에 대해 살펴볼 것이다.

예를 들어 0과 1을 나타내는 MNIST 이미지에 대해 내적을 계산해보자.

from sklearn.datasets import load_digits
import matplotlib.gridspec as gridspec

digits = load_digits()
d1 = digits.images[0]
d2 = digits.images[10]
d3 = digits.images[1]
d4 = digits.images[11]
v1 = d1.reshape(64, 1)
v2 = d2.reshape(64, 1)
v3 = d3.reshape(64, 1)
v4 = d4.reshape(64, 1)

plt.figure(figsize=(9, 9))
gs = gridspec.GridSpec(1, 8, height_ratios=[1],
                       width_ratios=[9, 1, 9, 1, 9, 1, 9, 1])
for i in range(4):
    plt.subplot(gs[2 * i])
    plt.imshow(eval("d" + str(i + 1)), aspect=1,
               interpolation='nearest', cmap=plt.cm.bone_r)
    plt.grid(False)
    plt.xticks([])
    plt.yticks([])
    plt.title("image {}".format(i + 1))
    plt.subplot(gs[2 * i + 1])
    plt.imshow(eval("v" + str(i + 1)), aspect=0.25,
               interpolation='nearest', cmap=plt.cm.bone_r)
    plt.grid(False)
    plt.xticks([])
    plt.yticks([])
    plt.title("vector {}".format(i + 1))
plt.tight_layout()
plt.show()

"0" 이미지와 "0" 이미지, 또는 "1" 이미지와 "1" 이미지의 내적값은 다음과 같다.

(v1.T @ v2)[0][0], (v3.T @ v4)[0][0]

(3064.0, 3661.0)

상대적으로 "0" 이미지와 "1" 이미지, 또는 "1" 이미지와 "0" 이미지의 내적값은 작다.

(v1.T @ v3)[0][0], (v1.T @ v4)[0][0], (v2.T @ v3)[0][0], (v2.T @ v4)[0][0]

(1866.0, 1883.0, 2421.0, 2479.0)

연습 문제 2.2.3

다음 코드를 실행하면 MNIST 숫자 이미지 전체 데이터를 모두 벡터로 변환하여 하나의 넘파이 행렬 X를 만든다.

이 행렬을 이용하여 다음 문제를 풀어라.

from sklearn.datasets import load_digits

X = load_digits().data

(1) 내적을 이용하여 첫 번째 이미지와 10번째 이미지의 유사도를 구하라.

(2) 내적을 이용하여 모든 이미지의 조합에 대해 유사도를 구하라. 어떻게 구현하는 것이 효율적일까? (힌트 : 이 문제는 뒤에서 배울 행렬과 행렬의 곱셈을 이용한다.)

import numpy as np  # 넘파이 패키지 임포트
import matplotlib.pylab as plt  # 맷플롯립 패키지 임포트
from sklearn.datasets import load_digits
import time
X = load_digits().data
print(type(X), X.shape )
print(X[0] @ X[9]) # (1) 내적으로 얻은 코싸인 유사도
# i 번째 이미지와 j 번째 이미지의 내적값을 i행 j열 성분으로 갖는 행렬 P
# 행렬 P는 1797 x 1797 짜리 정방행렬이고
# i행 j열 성분과 j행 i열 성분은 같으므로 대칭행렬이다.
start = time.time()
P = np.ones((1797, 1797))
for i in range(1797):
    for j in range(i+1):
        P[i][j] = X[i] @ X[j]
        if i != j:
            P[j][i] = P[i][j]
print("for문으로 계산하는데 걸린 시간:", f"{time.time()-start:.4f} sec")
print(P.shape, P[0][9]) # (1)에서 구한 유사도와 (2)에서 구한 유사도 비교/검증
# (3) X와 X.T의 행렬곱으로 계산
start = time.time()
Q = X @ X.T
print("행렬곱으로 계산하는데 걸린 시간:", f"{time.time()-start:.4f} sec")
print(Q.shape, Q[0][9]) # (1)(2)에서 구한 유사도와 (3)에서 구한 유사도 비교/검증
# 벡터, 행렬 계산이 for문보다 훨씬 빠름을 알 수 있다. 

<class 'numpy.ndarray'>
(1797, 64) 
2807.0 
for문으로 계산하는데 걸린 시간: 4.6719 sec 
(1797, 1797) 2807.0 
행렬곱으로 계산하는데 걸린 시간: 0.0358 sec 
(1797, 1797) 2807.0

선형회귀 모형

선형회귀 모형(linear regression model)이란 독립변수 $x$에서 종속변수 $y$를 예측하는 방법의 하나로 독립변수 벡터 $x$와 가중치 벡터 $w$와의 가중합으로 ${y}$에 대한 예측값 $\hat{y}$를 계산하는 수식을 말한다.

이 수식에서 기호 ^는 "캐럿(caret)"이라는 기호이다. $\hat{y}$는 "와이 햇(y hat)"이라고 읽는다.

이 수식은 다음처럼 벡터의 내적으로 나타낼 수 있다.

선형회귀 모형은 가장 단순하면서도 가장 널리 쓰이는 예측 모형이다.

예를 들어 어떤 아파트 단지의 아파트 가격을 조사하였더니 아파트 가격은 (1)면적, (2)층수, (3)한강이 보이는지의 여부, 즉 이 세 가지 특징에 의해 달라진다는 사실을 알게 되었다. 이때 이 단지 내의 아파트 가격을 예측하는 예측 모형을 다음과 같이 만들 수 있다.

• 면적($m^2$)을 입력 데이터 $x_1$라고 한다.

• 층수를 입력 데이터 $x_2$라고 한다

• 한강이 보이는지의 여부를 입력 데이터 $x_3$라고 하며 한강이 보이면 $x_3 = 1$, 보이지 않으면 $x_3 = 0$이라고 한다.

• 출력 데이터 $\hat{y}$는 해당 아파트의 예측 가격이다.

위와 같이 입력 데이터와 출력 데이터를 정의하고 회귀분석을 한 결과, 아파트값이 다음과 같은 선형회귀 모형으로 나타난다고 가정하자. 이러한 모형을 실제로 찾는 방법은 나중에 회귀분석 파트에서 공부하게 된다.

이 모형은 다음과 같이 해석할 수 있다.

• 면적이 1$m^2$ 증가할수록 가격은 500만 원이 증가한다.

• 층수가 1층 높아질수록 가격은 200만 원이 증가한다.

• 한강이 보이는 집은 1,000만 원의 웃돈(프리미엄)이 존재한다.

위 식은 다음과 같이 벡터의 내적으로 고쳐 쓸 수 있다.

즉, 위 선형회귀 모형은 다음 가중치 벡터로 대표된다.

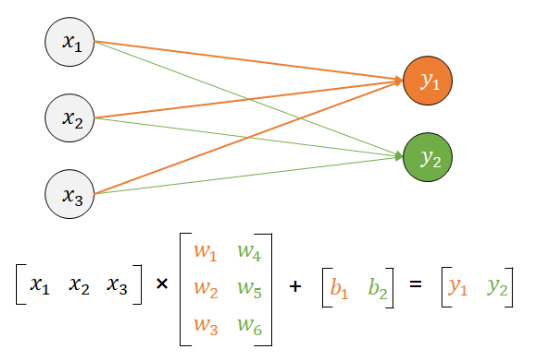
인공신경망(artificial neural network)에서는 선형회귀 모형을 다음과 같은 그림으로 표현한다. 데이터는 노드(node) 혹은 뉴런(neuron)이라는 동그라미로 표시하고 곱셈은 선분(line)위에 곱할 숫자를 써서 나타낸다. 덧셈은 여러 개의 선분이 만나는 것으로 표시한다.

선형회귀 모형의 단점

선형회귀 모형은 비선형적인 현실 세계의 데이터를 잘 예측하지 못할 수 있다는 단점이 있다. 예를 들어 집값은 면적에 단순 비례하지 않는다. 소형 면적의 집과 대형 면적의 집은 단위 면적당 집값의 증가율이 다를 수 있다. 또한 저층이 보통 고층보다 집값이 싸지만 층수가 올라갈수록 정확히 층수에 비례하여 가격이 증가하지도 않는다.

이러한 현실 세계의 데이터와 선형회귀 모형의 괴리를 줄이기 위해 선형회귀 모형이 아닌 완전히 다른 모형을 쓰기보다는 선형회귀 모형을 기반으로 여러 기법을 사용해 수정한 모형을 사용하는 것이 일반적이다. 이러한 수정 선형회귀 모형에 대해서는 나중에 공부하게 된다.

제곱합

데이터의 분산(variance)이나 표준 편차(standard deviation) 등을 구하는 경우에는 각각의 데이터를 제곱한 뒤 이 값을 모두 더한 제곱합(sum of squares)을 계산해야 한다. 이 경우에도 벡터의 내적을 사용하여 $x^Tx$로 쓸 수 있다.

행렬과 행렬의 곱셈

벡터의 곱셈을 정의한 후에는 이를 이용하여 행렬의 곱셈을 정의할 수 있다. 행렬과 행렬을 곱하면 행렬이 된다. 방법은 다음과 같다.

$A$ 행렬과 $B$ 행렬을 곱한 결과가 $C$ 행렬이 된다고 하자.

$C$의 $i$번째 행, $j$번째 열의 원소 $c_{ij}$의 값은 $A$ 행렬의 $i$번째 행 벡터 $a_i^T$와 $B$ 행렬의 $j$번째 열 벡터 $b_j$의 곱이다.

이 정의가 성립하려면 앞의 행렬 $A$의 열의 수가 뒤의 행렬 $B$의 행의 수와 일치해야만 한다.

다음은 $4 \times 3$ 행렬과 $3 \times 2$을 곱하여 $4 \times 2$을 계산하는 예다.

다음은 실제 행렬을 사용한 곱셈의 예다.

넘파이를 이용하여 행렬의 곱을 구할 때도 @ 연산자 또는 dot() 명령을 사용한다.

A = np.array([[1, 2, 3], [4, 5, 6]])
B = np.array([[1, 2], [3, 4], [5, 6]])
C = A @ B
C

array([[22, 28],
       [49, 64]])

연습 문제 2.2.4

(1) $A$와 $B$가 위와 같을 때 $AB$를 연습장에 손으로 계산하고 넘파이의 계산 결과와 맞는지 확인한다.

(2) 순서를 바꾸어 $BA$를 손으로 계산하고 넘파이의 계산 결과와 맞는지 확인한다. $BA$가 $AB$와 같은가?

(3) $A$, $B$가 다음과 같을 때, $AB$, $BA$를 (계산이 가능하다면) 손으로 계산하고 넘파이의 계산 결과와 맞는지 확인한다. $AB$, $BA$ 모두 계산 가능한가?

(4) $A$, $B$가 다음과 같을 때, $AB$, $BA$를 (계산이 가능하다면) 손으로 계산하고 넘파이의 계산 결과와 맞는지 확인한다. $AB$, $BA$ 모두 계산 가능한가? $BA$의 결과가 $AB$와 같은가?

(5) $A$가 다음과 같을 때, $AA^T$와 $A^TA$를 손으로 계산하고 넘파이의 계산 결과와 맞는지 확인한다. $AA^T$와 $A^TA$의 크기는 어떠한가? 항상 정방행렬이 되는가?

(6) $x$가 다음과 같을 때, $x^Tx$와 $xx^T$를 손으로 계산하고 넘파이의 계산 결과와 맞는지 확인한다. $x^Tx$와 $xx^T$의 크기는 어떠한가? 어떤 것이 스칼라이고 어떤 것이 정방행렬인가?

---

import numpy as np
A = np.array([[1, 2, 3], [4, 5, 6]])
B = np.array([[1, 2], [3, 4], [5, 6]])
# (1)
print("(1)", A @ B)
# (2) 다르다. shape부터가 다르다.
print("(2)", B @ A)
# (3) B @ A 는 Shape이 맞지 않기 때문에 계산 불가
A = np.array([1, 2, 3])
B = np.array([[4, 7], [5, 8], [6, 9]])
print("(3)", A @ B)
# (4) 행렬곱은 교환법칙 성립하지 않는다.
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
print("(4)", A @ B, B @ A )
# (5) Transpose를 취하면 자기 자신이므로 항상 정방행렬이다. 
A = np.array([[1, 2], [3, 4], [5, 6]])
print("(5)", A @ A.T, A.T @ A )
# (6) 둘 다 정방행렬이고, 전자만 스칼라
x = np.array([1,2,3]).reshape(3,1)
print("(6)", x.T@x, x@x.T)

---

인공 신경망은 내부적으로 다음과 같이 여러 개의 선형회귀 모형을 사용한다. 이 구조는 행렬과 벡터의 곱으로 나타낼 수 있다.

위 그림을 행렬식으로 표현하면 다음과 같다.

그림에서 벡터 $x$를 열벡터가 아닌 행벡터로 표현된 이유는 데이터의 개수가 많아졌을 때 input 데이터를 행렬로 표현하기 위함이다. 이에 대해 나중에 배우게 되나, 아래 그림과 참조 링크에서 확인할 수 있다.

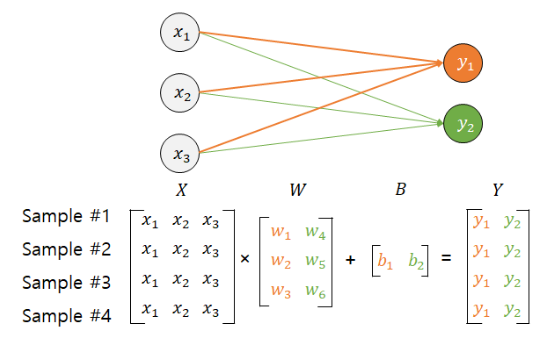
참조: 행렬곱으로 병렬 연산 이해하기

교환 법칙과 분배 법칙

행렬의 곱셈은 곱하는 행렬의 순서를 바꾸는 교환 법칙이 성립하지 않는다. 그러나 덧셈에 대한 분배 법칙은 성립한다.

$A$, $B$, $C$가 다음과 같을 때 위 법칙을 넘파이로 살펴보자.

A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
C = np.array([[9, 8], [7, 6]])

$AB$ 와 $BA$의 값은 다음처럼 다른 값이 나오므로 교환법칙이 성립하지 않음을 알 수 있다.

A @ B

array([[19, 22],
       [43, 50]])

B @ A

array([[23, 34],
       [31, 46]])

분배법칙은 다음과 같이 성립한다.

A @ (B + C)

array([[42, 42],
       [98, 98]])

A @ B + A @ C

array([[42, 42],
       [98, 98]])

(A + B) @ C

array([[110,  96],
       [174, 152]])

A @ C + B @ C

array([[110,  96],
       [174, 152]])

전치 연산도 마찬가지로 덧셈/뺄셈에 대해 분배 법칙이 성립한다.

전치 연산과 곱셈의 경우에는 분배 법칙이 성립하기는 하지만 전치 연산이 분배되면서 곱셈의 순서가 바뀐다.

마찬가지로 넘파이로 위 법칙이 성립하는지 살펴보자.

(A + B).T

array([[ 6, 10],
       [ 8, 12]])

A.T + B.T

array([[ 6, 10],
       [ 8, 12]])

(A @ B).T

array([[19, 43],
       [22, 50]])

B.T @ A.T

array([[19, 43],
       [22, 50]])

---

연습 문제 2.2.5

(1) 길이가 같은 일벡터 $1_N \in \mathbf{R}^N$와 행벡터 $x \in \mathbf{R}^N$의 곱은 행벡터 $x$를 반복하여 가지는 행렬과 같음을 보여라.

---

✒️
좌변을 풀어서 보면

이고 행렬의 사이즈는 N x 1 과 1 x N 의 행렬곱이므로 N x N 행렬이 됨을 알 수 있다. 각 element 별로 살펴보면 행렬곱의 결과가 (2.2.62) 와 같이 됨을 알 수 있다.

---

(2) 행렬 $X \,( X \in \mathbf{R}^{N \times M})$가 있을 때, 이 행렬의 각 열의 평균으로 이루어진 벡터 $\bar{x}\,( \bar{x} \in \mathbf{R}^{M})$가 다음과 같음을 보여라.

---

✒️
행렬 $X$는 M개의 Feature 들을 갖는 데이터가 N개 모인 데이터셋으로 볼 수 있다. 각 Feature 들의 합을 원소로 갖는 벡터 $X^T\mathbf{1}_N$를 데이터의 개수 $N$으로 나눠주기 위해 $N$의 역수를 앞에 곱해주면 각 Feature 들의 평균값을 원소로 갖는 열벡터가 얻어진다.

---

(3) 행렬 $\bar{X}\ ( \bar{X} \in \mathbf{R}^{N \times M})$는 동일한 벡터 $\bar{x}^T$를 $N$개 누적하여 만든 행렬이다. 즉 각 열의 모든 값이 그 열의 평균으로 이루어진 행렬이다.

이때 $\bar{X}$가 다음과 같음을 보여라.

---

✒️
(1), (2)에 의해 좌변은 $\mathbf{1}_N^{} \bar{x}^T=\dfrac{1}{N}\mathbf{1}_N (X^T \mathbf{1}_N)^T$ 이고 전치연산의 분배는 행렬 곱의 순서를 반대로 만드는 성질, 행렬에 전치 연산을 2번 하면 자기 자신이 되는 성질에 의해 우변과 같이 변형된다.

---

(4) 다음 코드를 실행하면 붓꽃 전체 데이터를 모두 벡터로 변환하여 하나의 넘파이 행렬 X 를 만든다.

from sklearn.datasets import load_iris

X = load_iris().data

이 데이터로 행렬 $\bar{X}$의 값을 계산하라. 이 행렬은 첫 번째 열의 값이 모두 같은 값으로 붓꽃의 꽃받침의 길이(sepal length)의 평균이고 두 번째 열의 값이 모두 같은 값으로 붓꽃의 꽃받침의 폭(sepal width)의 평균, 이런 식으로 계산된 행렬이다.

---

✒️

import numpy as np
from sklearn.datasets import load_iris
X = load_iris().data 
# 위의 연습문제에서 N = 150 이고 M = 4 인 경우에 해당한다.
N = 150
Y = ( np.ones((N, 1)) @ np.ones((N, 1)).T @ X ) / N
print(Y)

---

곱셈의 연결

연속된 행렬의 곱셈은 계산 순서를 임의의 순서로 해도 상관없다.

---

연습 문제 2.2.6

다음 행렬의 곱셈을 순서를 바꾸어 두 가지 방법으로 해본다.

---

✒️

항등행렬의 곱셈

어떤 행렬이든 항등행렬을 곱하면 그 행렬의 값이 변하지 않는다.

넘파이로 다음과 같이 확인한다.

A = np.array([[1, 2], [3, 4]])
I = np.eye(2)

A @ I

array([[1., 2.],
       [3., 4.]])

I @ A

array([[1., 2.],
       [3., 4.]])

행렬과 벡터의 곱

그럼 이러한 행렬의 곱셈은 데이터 분석에서 어떤 경우에 사용될까? 행렬의 곱셈 중 가장 널리 쓰이는 것은 다음과 같은 형태의 행렬 $M$과 벡터 $v$의 곱이다.

벡터와 행렬의 크기를 직사각형으로 표시하면 다음과 같다.

행렬과 벡터의 곱을 사용하는 몇가지 예를 살펴보자.

열 벡터의 선형조합

행렬 $X$와 벡터 $w$의 곱은 행렬 $X$를 이루는 열벡터 $c_1, c_2, \ldots, c_M$을 뒤에 곱해지는 벡터 $w$의 각 성분 $w_1, w_2, \ldots, w_M$으로 선형조합(linear combination)을 한 결과 벡터와 같다.

연습 문제 2.2.7

다음 행렬 $X$와 벡터 $w$에 대해 곱 $Xw$가 열벡터 $c_1, c_2, c_3$의 선형조합 $w_1c_1 + w_2c_2 + w_3c_3$가 됨을 실제 계산으로 증명하라.

✒️

import numpy as np
x = np.array([1,2,3,4,5,6]).reshape(2,3)
w = np.array([2,3,4]).reshape(3,1)
xw = (x@w).reshape(2,1)
lc = (x[:,0]* w[0] + x[:,1] * w[1] + x[:,2] * w[2]).reshape(2,1)
print(x@w)
print(lc)

연습 문제 2.2.8

벡터 $v_1, v_2, v_3$로 이루어진 행렬 $V$와 벡터 $\lambda$에 대해 다음 식이 성립함을 증명하라. 이 식에서 $\lambda_1$는 스칼라이다.

✒️
행렬과 벡터의 곱을 행렬을 이루는 열벡터의 선형결합으로 해석할 때, $v2$, $v3$에 곱해지는 상수값이 0 인 경우이므로, (2.2.75) 식처럼 된다.

벡터의 선형조합은 다양한 분야에 응용된다. 예를 들어 두 이미지 벡터의 선형조합은 두 이미지를 섞어놓은 모핑(morphing) 효과를 얻는 데 사용할 수 있다.

모핑(morphing)이란?

from sklearn.datasets import fetch_olivetti_faces

faces = fetch_olivetti_faces()

f, ax = plt.subplots(1, 3)

ax[0].imshow(faces.images[6], cmap=plt.cm.bone)
ax[0].grid(False)
ax[0].set_xticks([])
ax[0].set_yticks([])
ax[0].set_title("image 1: $x_1$")

ax[1].imshow(faces.images[10], cmap=plt.cm.bone)
ax[1].grid(False)
ax[1].set_xticks([])
ax[1].set_yticks([])
ax[1].set_title("image 2: $x_2$")

new_face = 0.7 * faces.images[6] + 0.3 * faces.images[10]
ax[2].imshow(new_face, cmap=plt.cm.bone)
ax[2].grid(False)
ax[2].set_xticks([])
ax[2].set_yticks([])
ax[2].set_title("image 3: $0.7x_1 + 0.3x_2$")

plt.show()

여러 개의 벡터에 대한 가중합 동시 계산

벡터 하나의 가중합은 $w^Tx$ 또는 $x^Tw$로 표시할 수 있다는 것을 배웠다. 그런데 만약 이렇게 $w$ 가중치를 사용한 가중합을 하나의 벡터 $x$가 아니라 여러 벡터 $x_1, \cdots, x_M$ 개에 대해서 모두 계산해야 한다면 어떻게 해야 할까? 예를 들어 위와 같이 선형 회귀 모형을 사용하여 여러 데이터 $x_1, x_2, x_3, \cdots, x_N$ 개의 데이터 모두에 대해 예측값 $y_1, y_2, y_3, \cdots, y_N$을 한꺼번에 계산하고 싶다면 다음처럼 데이터 행렬 $X$를 사용하여 $\hat{y} = Xw$라는 수식으로 간단하게 표시할 수 있다.

즉.

연습 문제 2.2.9

$x_1$, $x_2$가 다음과 같을 때,

다음 등식이 성립함을 보인다.

✒️
문제 자체가 너무 자명하기 때문에
난수를 발생시켜서 등식이 성립함을 검증하는 코드를 작성했다.

import numpy as np
x1 = np.random.randint(1,100,3).reshape(3,1)
x2 = np.random.randint(1,100,3).reshape(3,1)
w = np.random.randint(1,100,3).reshape(3,1)
X = np.array([x1,x2]).reshape(2,3)
print(X @ w == np.array([x1.T @ w, x2.T @ w]).reshape(2,1))

잔차

선형 회귀분석(linear regression)을 한 결과는 가중치 벡터 $w$라는 형태로 나타나고 예측치는 이 가중치 벡터를 사용한 독립변수 데이터 레코드 즉, 벡터 $x_i$의 가중합 $w^Tx_i$이 된다고 했다. 예측치와 실젯값(target) $y_{i}$의 차이를 오차(error) 혹은 잔차(residual) $e_i$라고 한다. 이러한 잔찻값을 모든 독립변수 벡터에 대해 구하면 잔차 벡터 $e$가 된다.

잔차 벡터는 다음처럼 $y-Xw$로 간단하게 표기할 수 있다.

잔차 제곱합

잔차의 크기는 잔차 벡터의 각 원소를 제곱한 후 더한 잔차 제곱합(RSS: Residual Sum of Squares)을 이용하여 구한다. 이 값은 $e^Te$로 간단하게 쓸 수 있으며 그 값은 다음처럼 계산한다.

연습 문제 2.2.10

분배 법칙을 사용하여 위 식 $(y - Xw)^T (y - Xw)$을 풀어쓰면 다음과 같아짐을 보여라.

✒️
전치 연산 해주고(좌변에서 $Xw$를 전치하면 순서가 바뀌어서 $w^T X^T$가 되는 것에 주의), 분배법칙에 따라 순서대로 잘 곱하면 식 2.2.84 처럼 나온다.

이차형식

위의 연습 문제에서 마지막 항은 $w^TX^TXw$라는 형태다. 이 식에서 $X^TX$는 정방행렬이 되므로 이 정방행렬을 $A$라고 이름 붙이면 마지막 항은 $w^TAw$와 같은 형태가 된다.

벡터의 이차형식(Quadratic Form)이란 이처럼 어떤 벡터와 정방행렬이 '행벡터 $\times$ 정방행렬 $\times$ 열벡터'의 형식으로 되어 있는 것을 말한다.

이 수식을 풀면 $i=1,\ldots,N, j=1,\ldots,N$에 대해 가능한 모든 $i,j$ 쌍의 조합을 구한 다음 $i$, $j$에 해당하는 원소 $x_i$, $x_j$를 가중치 $a_{i,j}$와 같이 곱한 값 $a_{i,j}x_ix_j$의 총합이 된다.

이차 형식 더 알아보기

연습 문제 2.2.11

다음 3차원 벡터와 행렬에 대해 이차형식을 쓰고 값을 계산하라.

✒️
이차형식: $x^TAx$
값: $a_{11}x_{11}+a_{12}x_{12}+a_{13}x_{13}+a_{21}x_{21}+a_{22}x_{22}+a_{23}x_{23}+a_{31}x_{31}+a_{32}x_{32}+a_{33}x_{33}$
(where $x_{ij}=x_ix_j$)

예를 들어 $ x = [1, 2, 3]^T $ 이고 A가 다음과 같다면

넘파이 에서 벡터의 이차형식은 다음처럼 계산한다.

x = np.array([1, 2, 3])
x

array([1, 2, 3])

A = np.arange(1, 10).reshape(3, 3)
A

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

x.T @ A @ x

228

연습 문제 2.2.12

다음 식이 성립함을 증명하라.

✒️
우선, 문제에 주어져 있지 않지만 우변에서 $A + A^T$ 덧셈 연산이 가능하려면 $A$는 반드시 정방행렬이어야 하고, 벡터 $x$ 도 $A$에 대해 적당한 사이즈라고 가정하자.
주어진 등식의 우변을 전개하고 정리하면 $x^TAx = x^TA^Tx$ 이 되고 좌, 우변은 각각 이차형식 꼴이다. 좌변을 $\sum_{i=1}^{N} \sum_{j=1}^{N} a_{i,j} x_i x_j$ 라 하면, 덧셈과 곱셈은 각각 교환법칙이 성립하므로 $\sum_{j=1}^{N} \sum_{i=1}^{N} a_{i,j} x_j x_i$ 와 같고, 첨자 i, j만 서로 바꿔주면 이차형식 $x^TA^Tx$을 나타내는 식이 되므로 등식이 성립한다.

부분행렬

다음과 같은 2차원 정방행렬 $A$, $B$가 있다.

이때 두 행렬의 곱 $AB$는 $A$, $B$의 부분행렬(submatrix)을 이용하여 여러 방법으로 계산할 수 있다.

(1) 우선 앞에 곱해지는 행렬을 행벡터로 나누어 계산해도 된다.

즉,

이면

(2) 아니면 뒤에 곱해지는 행렬을 열벡터로 나누어 계산해도 된다.

즉,

이면

(3) 앞에 곱해지는 행렬을 열벡터로, 뒤에 곱해지는 행렬을 행벡터로 나누어 스칼라처럼 계산해도 된다.

벡터의 크기를 직사각형으로 표시하면 다음과 같다.

여기에서는 2차원 행렬의 예를 들었지만 일반적인 $N$차원 행렬에서도 이 관계는 성립한다.

연습 문제 2.2.13

행렬 $V$는 열벡터 $v_i\;(i=1,\ldots,N)$로 이루어진 정방행렬이다. $V$와 크기가 같은 다른 정방행렬 $A$, $\Lambda$이 있을 때 다음 식이 성립한다.

$N=3$인 경우에 위 식이 성립함을 보여라.

✒️

# 자명하기 때문에 난수를 발생시켜 검증
import numpy as np
A = np.random.randint(1,100,9).reshape(3,3)
H = np.diag(np.random.randint(1,100,3))
v1 = np.random.randint(1,100,3).reshape(3,1)
v2 = np.random.randint(1,100,3).reshape(3,1)
v3 = np.random.randint(1,100,3).reshape(3,1)
V = np.hstack([v1, v2, v3]).reshape(3,3)
print(A @ V == np.hstack([A @ v1, A @ v2, A @ v3]))
print(V @ H == np.hstack([H[0,0] * v1, H[1,1] * v2, H[2,2] * v3]))

연습 문제 2.2.14

부분행렬 공식 (3)으로부터 $A$가 행벡터 $a_i^T\;(i=1,\ldots,N)$로 이루어진 $N$차 정방행렬일 때

다음 관계가 성립한다.

$N=3$인 경우에 위 식이 성립함을 보여라.

✒️
$A = \begin{bmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{bmatrix}$ 라 하자.

$A^T = \begin{bmatrix}a_{11} & a_{21} & a_{31} \\a_{12} & a_{22} & a_{32} \\a_{13} & a_{23} & a_{33}\end{bmatrix}$

좌변: $A^TA = \begin{bmatrix}a_{11} & a_{21} & a_{31} \\a_{12} & a_{22} & a_{32} \\a_{13} & a_{23} & a_{33}\end{bmatrix}\begin{bmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{bmatrix}\dots(1)$

우변: $\sum_{i=1}^3 a_ia_i^T=a_1a_1^T+a_2a_2^T+a_3a_3^T$

$=\begin{bmatrix} a_{11} \\ a_{12} \\ a_{13} \end{bmatrix}\begin{bmatrix} a_{11} & a_{12} & a_{13} \end{bmatrix}+\begin{bmatrix} a_{21} \\ a_{22} \\ a_{23} \end{bmatrix}\begin{bmatrix} a_{21} & a_{22} & a_{23} \end{bmatrix}+\begin{bmatrix} a_{31} \\ a_{32} \\ a_{33} \end{bmatrix}\begin{bmatrix} a_{31} & a_{32} & a_{33} \end{bmatrix}\dots(2)$

(1), (2) 를 전개하면 같다.