사이킷런의 PCA 기능
사이킷런의 decomposition 서브패키지는 PCA 분석을 위한 PCA 클래스를 제공한다. 사용법은 다음과 같다.
-
입력 인수:
n_components: 정수
-
메서드:
-
fit_transform(): 특징행렬을 낮은 차원의 근사행렬로 변환 -
inverse_transform(): 변환된 근사행렬을 원래의 차원으로 복귀
-
-
속성:
-
mean_: 평균 벡터 -
components_: 주성분 벡터
다음 코드는 붓꽃 데이터를 1차원으로 차원축소(근사)하는 예제 코드다.
fit_transform() 메서드로 구한 X_low는 1차원 근사 데이터의 집합이다. 이 값을 다시 inverse_transform() 메서드에 넣어서 구한 X2는 다시 2차원으로 복귀한 근사 데이터의 집합이다.
from sklearn.decomposition import PCA
pca1 = PCA(n_components=1)
X_low = pca1.fit_transform(X)
X2 = pca1.inverse_transform(X_low)
plt.figure(figsize=(7, 7))
ax = sns.scatterplot(0, 1, data=pd.DataFrame(X), s=100, color=".2", marker="s")
for i in range(N):
d = 0.03 if X[i, 1] > X2[i, 1] else -0.04
ax.text(X[i, 0] - 0.065, X[i, 1] + d, "표본 {}".format(i + 1))
plt.plot([X[i, 0], X2[i, 0]], [X[i, 1], X2[i, 1]], "k--")
plt.plot(X2[:, 0], X2[:, 1], "o-", markersize=10)
plt.plot(X[:, 0].mean(), X[:, 1].mean(), markersize=10, marker="D")
plt.axvline(X[:, 0].mean(), c='r')
plt.axhline(X[:, 1].mean(), c='r')
plt.grid(False)
plt.xlabel("꽃받침 길이")
plt.ylabel("꽃받침 폭")
plt.title("Iris 데이터의 1차원 차원축소")
plt.axis("equal")
plt.show()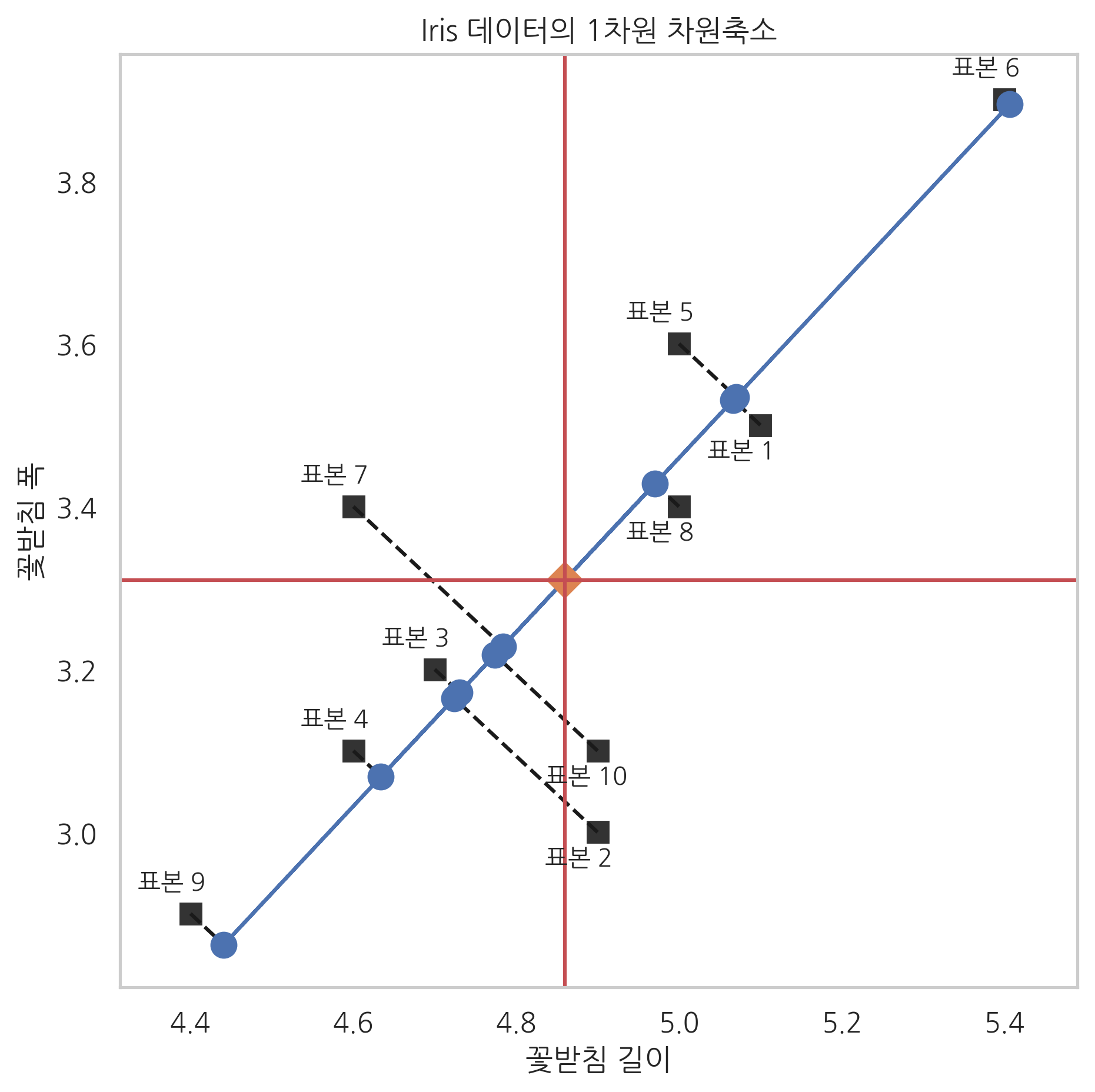
데이터의 평균값은 mean_ 속성으로 볼 수 있다.
pca1.mean_array([4.86, 3.31])
주성분 벡터 즉, 가장 근사 데이터를 만드는 단위기저벡터는 components_ 속성에서 구할 수 있다. 벡터의 값은 (0.68, 0.73)이다.
pca1.components_array([[0.68305029, 0.73037134]])
이 값은 평균을 제거한 특징행렬의 첫 번째 오른쪽 특이벡터 또는 그 행렬의 분산행렬의 첫 번째(가장 큰 고윳값에 대응하는) 고유벡터에 해당한다. 고유벡터의 부호 즉 방향은 반대가 될 수도 있다.
넘파이로 첫 번째 오른쪽 특이벡터를 구하면 (0.68, 0.73)임을 알 수 있다.
X0 = X - X.mean(axis=0)
U, S, VT = np.linalg.svd(X0)
VTarray([[-0.68305029, -0.73037134],
[-0.73037134, 0.68305029]])
VT[:, 0]array([-0.68305029, -0.73037134])
고유값 분해를 할 때는 넘파이가 고유값의 순서에 따른 정렬을 해주지 않으므로 사용자가 정렬해야 한다.
XCOV = X0.T @ X0
W, V = np.linalg.eig(XCOV)Warray([0.17107711, 1.44192289])
Varray([[-0.73037134, -0.68305029],
[ 0.68305029, -0.73037134]])
V[:, np.argmax(W)]array([-0.68305029, -0.73037134])
예를 들어 8번째 꽃의 꽃받침 길이와 꽃받침 폭은 다음과 같다.
X[7, :]array([5. , 3.4])
PCA로 구한 주성분의 값 즉, 꽃의 크기는 다음과 같다.
X_low[7]array([0.16136046])
이 값은 다음처럼 구할 수도 있다.
pca1.components_ @ (X[7, :] - pca1.mean_)array([0.16136046])
이 주성분의 값을 이용하여 다시 2차원 값으로 나타낸 근사값은 다음과 같다.
X2[7, :]array([4.97021731, 3.42785306])
연습 문제 3.5.1
붓꽃 데이터 중 앞에서 50개의 데이터(setosa 종)에 대해 다음 문제를 풀어라.
(1) 꽃잎의 길이와 꽃잎의 폭을 이용하여 1차원 PCA를 수행하라. 꽃의 크기는 꽃받침 길이와 꽃받침 폭의 어떤 선형조합으로 나타나는가?
(2) 꽃받침 길이와 폭, 꽃잎 길이와 폭, 이 4가지 변수를 모두 사용하여 1차원 PCA를 수행하라. 꽃의 크기는 관측 데이터의 어떤 선형조합으로 나타나는가?
✏️
import numpy as np
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
pca1 = PCA(n_components=1)
pca2 = PCA(n_components=1)
iris = load_iris()
N = 50 # 앞의 50송이 선택
X1 = iris.data[:N, :2] # 꽃받침 길이/폭만 선택
X2 = iris.data[:N, :4] # 꽃받침 길이/폭, 꽃잎 길이/폭 모두 선택
X1_low = pca1.fit_transform(X1) # x1_hat = W @ x1
X11 = pca1.inverse_transform(X1_low) # x11 = U @ x1_hat
X2_low = pca2.fit_transform(X2) # x2_hat = W @ x2
X22 = pca2.inverse_transform(X2_low) # x22 = U @ x2_hat
print("PCA로 구한 값")
print(pca1.components_)
print(pca2.components_)
print("--------")
print("평균을 제거한 특징행렬의 첫 번째 오른쪽 특이벡터로 검증")
X1_zeroMean = X1 - X1.mean(axis=0)
X2_zeroMean = X2 - X2.mean(axis=0)
U1, S1, VT1 = np.linalg.svd(X1_zeroMean)
U2, S2, VT2 = np.linalg.svd(X2_zeroMean)
print(VT1[:, 0])
print(VT2[:, 0])
print("--------")
print("평균을 제거한 특징행렬의 분산행렬의 가장 큰 고윳값에 대응하는 고유벡터로 검증")
X1_COV = X1_zeroMean.T @ X1_zeroMean
X2_COV = X2_zeroMean.T @ X2_zeroMean
W1, V1 = np.linalg.eig(X1_COV)
W2, V2 = np.linalg.eig(X2_COV)
# 고유분해는 직접 고윳값 크기에 따라 정렬해야 한다.
print(V1[:, np.argmax(W1)])
print(V2[:, np.argmax(W2)])PCA로 구한 값 [[0.67174957 0.74077832]] [[0.6690784 0.73414783 0.0965439 0.06356359]] -------- 평균을 제거한 특징행렬의 첫 번째 오른쪽 특이벡터로 검증 [-0.67174957 -0.74077832] [-0.6690784 0.59788401 0.43996277 -0.03607712] -------- 평균을 제거한 특징행렬의 분산행렬의 가장 큰 고윳값에 대응하는 고유벡터로 검증 [-0.67174957 -0.74077832] [0.6690784 0.73414783 0.0965439 0.06356359]
✏️
(1) 에서 꽃의 크기 = 0.67174957 꽃받침 길이 + 0.74077832 꽃받침 폭과 같은 선형결합으로 표현된다.
(2) 에서도 마찬가지로 꽃의 크기는 꽃받침 길이/폭, 꽃잎 길이/폭 앞에 각각 계수 0.6690784, 0.73414783, 0.0965439, 0.06356359 가 곱해져서 모두 더해진 선형결합으로 표현된다.
✏️
꽃의 크기는 대체로 꽃받침의 폭과 길이에 의해 결정된다고 해석할 수 있다.
