4.1 vector space and its basis

다음은 etl.snu의 공학수학1 강의를 듣고 정리한 내용입니다

4.1 vector space and its basis

vector space

• 벡터 공간; 벡터들의 "집합"
• vector space V는 Rn 공간(컬럼 벡터들이 모인)의 부분집합인 벡터 공간
  • 굳이 집합이 아닌 "space"라는 말을 쓰는 이유?
    1. v1+v2 ∈V for any v1,v2∈ V
    2. cv1 ∈V for any v1∈V, c∈R

예1. R2 공간에는 무수히 많은 벡터들이 살고 있다.
빨간색 직선위에도 여러 벡터들이 살고 있는데, 이 빨간 직선에 속하는 임의의 아무 벡터이 1,2번 성질을 만족한다는 것을 알 수 있다.
이 때, 빨간색 직선은 R2에 대한 부분 집합으로 생각할 수 있다 (subspace; subset vector space)

• 한 벡터 공간의 부분 집합에서도 1,2번 성질을 만족할 경우, 그 부분집합; 벡터공간을 더 넓은 벡터 공간의 subspace라고 한다.
  예2. 평면 공간 또한 벡터 공간이다.
  평면 공간위의 아무 벡터를 가져와도 1,2번 성질을 만족한다
  예3. 원점 하나로 이루어진 벡터 공간위의, 0 벡터 또한 1,2의 성질을 만족한다.
  예4. x자 처럼 생긴 이 점들의 집합은 1,2번 성질을 만족하지 않기 때문에, 벡터 공간이 아니다.

벡터 공간이 되기 위해서는 반드시 원점을 포함해야 한다

• 2번 성질 때문
• 임의의 상수 c를 scalar multiplication을 해도 V라는 집합에 속해야 하는데,
  만약 c=0이면, 2번 성질을 만족하지 않기 때문이다.
• 원점이 그 집합안에 속해야한다(필요조건)

벡터 공간을 만드는 방법
예1. v1,...,vr ∈ Rn (벡터 공간을 생성하는 방식)
r개의 컬럼 벡터가 주어졌다. 주어진 컬럼 벡터에 대해서 scalar multiplication을 시행하여, 많은 벡터를 생성한다고 했을 때, 하나의 집합을 생성할 수 있다.
S={x: x= c1v1 + c2v2 + ... +crvr} -> 이 집합S가 벡터공간이 되는가?
how?
위의 집합S에서 임의의 x를 꺼내서 상수배를 한 뒤에도 S에 속하는 지 살펴본다.
1. x+y=(c1v1 + c2v2 + ... +crvr)+(c1v1 + c2v2 + ... +crvr)∈ V
2. k(x)=k(c1v1 + c2v2 + ... +crvr)∈ V
두 성질 모두를 만족시킨다.

{x: x= c1v1 + c2v2 + ... +crvr}= span{v1,...,vr}
span: {v1,...,vr}까지의 벡터들끼리 선형 조합해서 만들어지는 모든 벡터를 포함하는 집합

• 주어진 벡터의 span을 한것은 벡터 공간이 된다

예2. 원점을 지나는 어떤 직선이 있다. (원래의 커다란 Rn공간에서, 제한 조건을 첨가해서, 모든 제한 조건을 만족하는 벡터 공간을 도출하는 방식)
T={x:x1+x2=0} -> 벡터 공간이 되는가?
1. x+y=(x1+x2)+(y1+y2)=0+0=0∈ V
2. k(x)=k(x1+x2)=k(0)=0∈ V
두 성질을 모두 만족시킨다.

예3. 원점을 지나는 어떤 두 평면이 있다.
{x: x1+x2+x3=0 and x1-x2-x3=0} => {x:Ax=0} (행렬A를 이용해서 방정식의 계수를 담아보자)
이때 두 평면을 모두 만족시키는 직선은 원점을 지나므로 벡터 공간이 된다.

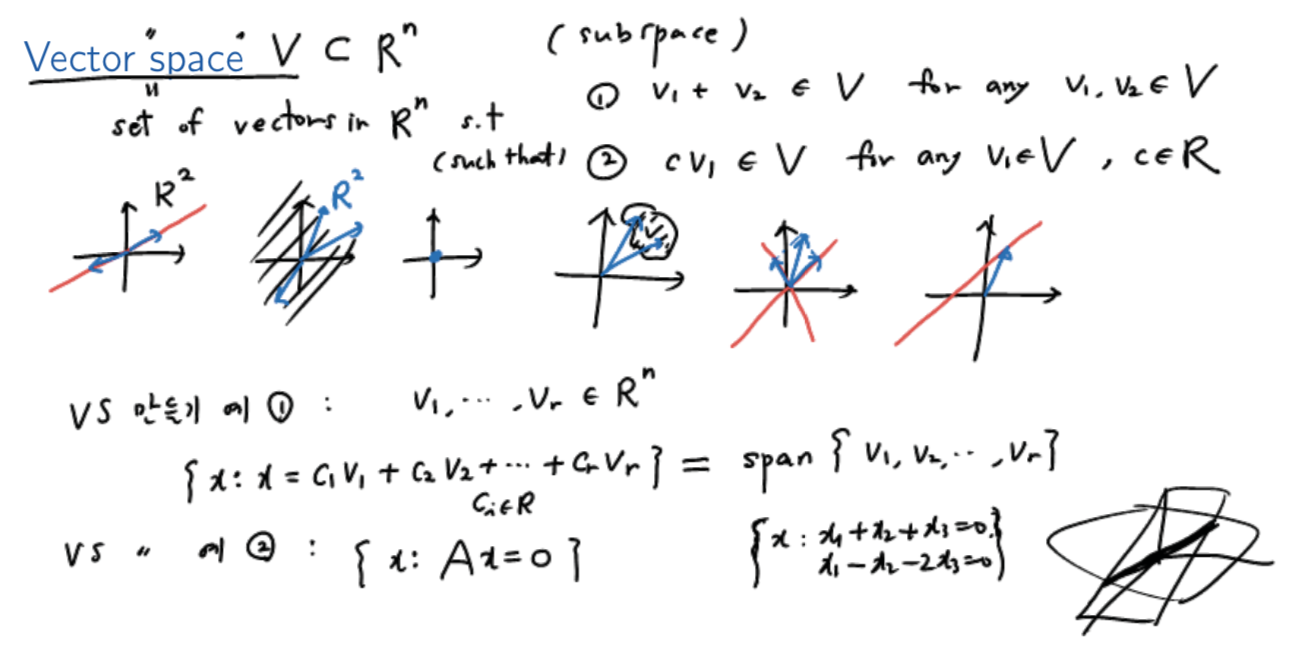
basis

• 기저: 벡터 공간의 특별한 벡터들을 모아놓은 집합
  • 단순히 벡터를 모아놓은 게 아니라,
    1. 선형 독립
    2. 주어진 벡터를 span하면 벡터 공간V를 만들 수 있다.