4.3 Existence and uniqueness of solutions

다음은 etl.snu의 공학수학1 강의를 듣고 정리한 내용입니다

4.3 Existence and uniqueness of solutions

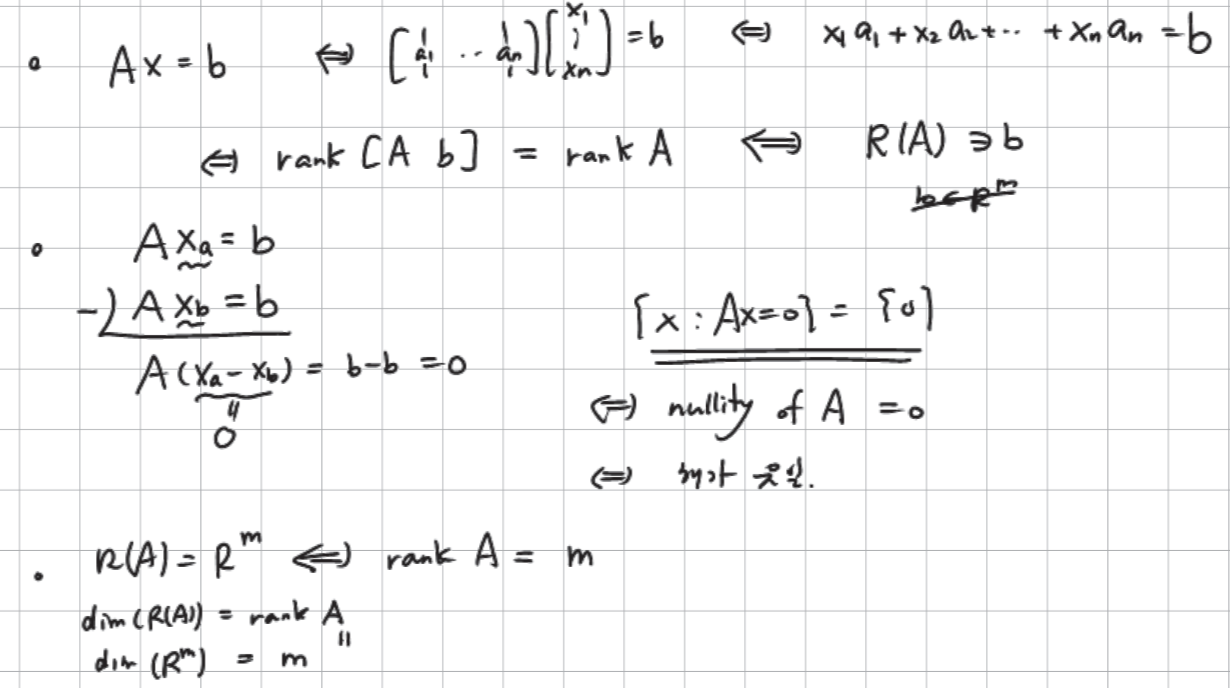
Existence

• b라는 컬럼 벡터는 a라는 컬럼벡터들의 선형조합으로 바꾸어 생각해볼 수 있다.
  즉, b는 a(i)벡터들에 대해서 독립일 수가 없다 -> b는 역할을 하지 못한다!
  -> rank[A b] =rank[A]

• A의 column space R(A) 안에 b가 들어간다!

Uniqueness

• A(x-y) =b-b =0 일 때,
  (x-y)라는 컬럼 벡터는 A의 null space에 속한다.
  만약 {x:Ax=0}={0}라면 (항상 0벡터만을 원소로 하면), <=> dim=0 <=> nullity(A)=0
  (x-y)=0
  x=y -> 해가 유일

Existence for any b in Rm

• b ∈ R(A) 이므로, 만약 b ∈ Rm 이라면,
• R(A) = Rm (가장 커봐야!) <=> rank A=m
  dim(R(A)) =rank A

Homogeneous case

• non trivial solution exists iff rank A =r < n
  • non trivial solution이 존재하려면, x=0 이외의 다른 해가 null space에 존재해야하고,
    null space의 dimension은 0보다 커지게 된다.
    -> nullity = n - rank A > 0
    -> rank A < n
• 방정식의 수(m) < 미지수의 수(n)
  • rank A < m < n => non trivial solution이 항상 존재