🟡 릿지 회귀란?
→ 규제가 추가된 선형 회귀 이다. 규제항 이 비용함수에 추가된다.
이 규제항은 학습 알고리즘을 데이터에 맞추는 것뿐만 아니라 모델의 가중치가 가능한 작게 유지되도록 한다.
규제항은 학습 훈련 시 비용함수에 추가된다. 모델의 훈련이 끝나면 규제가 없는 성능 지표로 평가한다.
하이퍼 파라미터 는 모델을 얼마나 규제할지 조절한다. 만약 0 일경우 선형 회귀와 같아진다.
가 아주 크면 가중치가 거의 0에 가까워지고, 데이터의 평균은 수평선이 된다.
매
🟨 매개 변수를 높이면
- 훈련 세트에서의 정확도 증가
- 데이터 포인트 하나하나에 집중
- 복잡도 증가
- 규제 감소
🟨 매개 변수를 낮추면
- 훈련세트에서의 정확도 감소
- 다수의 데이터 포인트에 집중
- 복잡도 감소
- 규제 증가
✔️ 릿지 회귀는 편향을 조금 더해주고, 분산을 줄이는 방법으로 정규화를 하는 것
🤔 선형 회귀와 뭐가 다를까?
가장 큰 차이점으로 복잡도를 제어할 수 있다!
각 특성들의 계수에 해당하는 가중치들을 적절하게 조절함으로써 가능하게 된다.
- 선형 회귀의 단점 : 모델이 지나치게 복잡해지면 과대적합의 문제가 발생하여 일반화가 곤란함 → 이를 지양하기 위해
모델의 복잡도와 관해 제약을 부여하였다.
릿지 회귀의 비용 함수
를 특성 가중치 벡터(~) 라고 하면 규제항은 오른쪽 식과 같다. 경사 하강법에 적용하려면 MSE 그라디언트 벡터에 를 더하면 된다
💡 계수를 제곱한 값을 기준으로 규제 적용
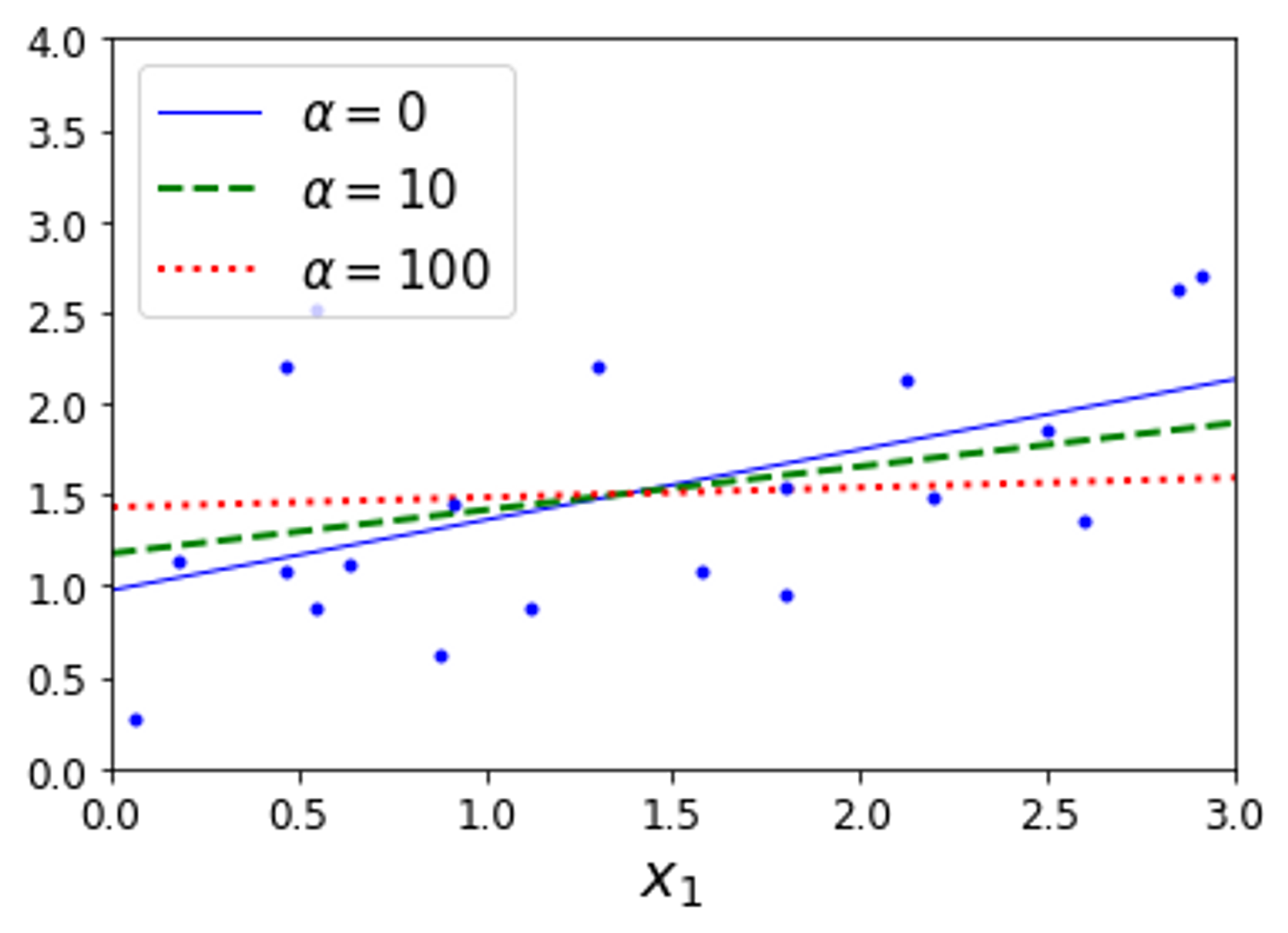
→ 선형 데이터에 값을 다르게 설정하여 릿지 모델을 돌린 결과이다. 평범한 릿지 모델을 사용하였다.
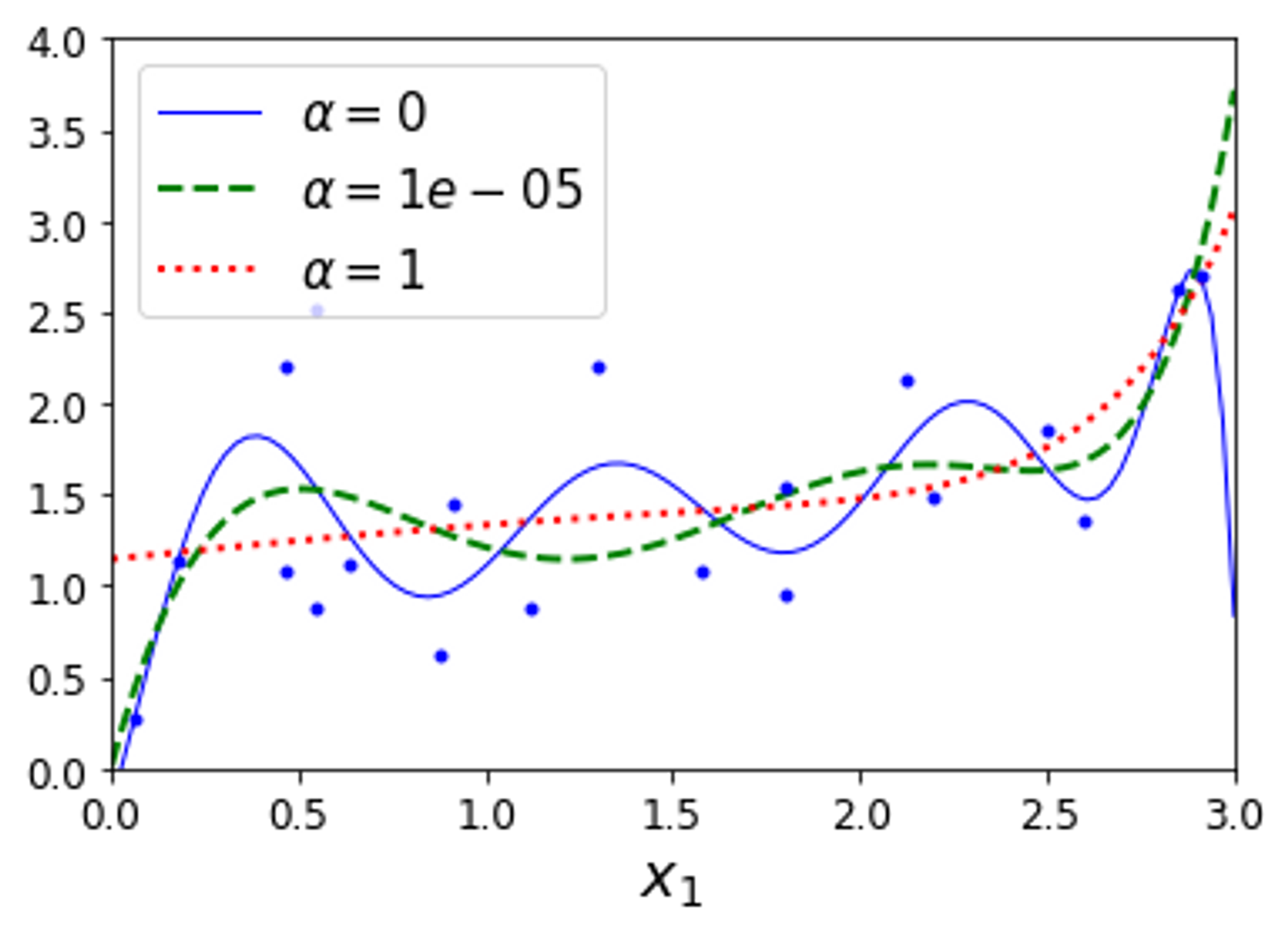
→ PolynomialFeatures(degree=10) 을 사용하여 데이터를 확장하고 , StandardScaler 을 사용하여 스케일을 조정한 후 릿지 모델을 사용하였다.
- ✅ 값을 증가시킬 수록 직선에 가까워진다. (⇒ 분산은 줄지만 편향은 커짐)
🟠 정규방정식을 사용한 릿지 회귀
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha = 1, solver = "cholesky")
ridge_reg.fit(X,y)
ridge_reg.predict([[1.5]])🟠 확률적 경사 하강법을 사용한 릿지 회귀
릿지 회귀에서도 또 다른 방식으로 확률적 경사 하강법을 사용할 수 있다.
이 경우에는 매 반복에서 딱 하나의 샘플을 무작위로 선택하고 그 샘플에 대한 그라디언트를 계산한다.
이렇게 하면 알고리즘이 덜 규제된 경향이 있다. 단, 배치 경사 하강법이나 미니배치 경사 하강법보다 불안정하다.
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty="l2", alpha=0.1)
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])⬜️ 패널티 값을 효과적으로 구하는 방법
릿지 회귀에서 적절한 패널티 값을 구하는 것은 매우 중요하다.
교차 검증(cross-validation)을 사용하여 검증실험을 진행하여 적절한 알파값을 확인할 수 있다.
sklearn에서 제공하는 RidgeCV를 사용하여 검증할 수 있다.
from sklearn.linear_model import RidgeCV
alphas = [0.01,0.05,0.1,0.2,1.0,10.0,100.0,500.0]
ridge = RidgeCV(alphas = alphas, normalize = True, cv = 3)
ridge.fit(ans[['x']],ans['y'])참조

