릿지회귀(Ridge Regression)

릿지회귀(Ridge Regression)

일반 선형회귀 모델을 사용하다 보면 과적합이 생길때가 빈번하게 있다. 이때, 과적합을 줄이기 위해서 사용하는것이 바로 릿지회귀이다.

$\beta_{ridge}$: $argmin[\sum_{i=1}^n(y_i - \beta_0 - \beta_1x_{i1}-\dotsc-\beta_px_{ip})^2 + \lambda\sum_{j=1}^p\beta_j^2]$
(y실제값에서 예측값을 뺀것의 제곱) + (람다)

우리가 과적합을 줄이기 위해서는 학습한 모델의 복잡도를 줄이것 즉, 특성을 줄이는것이다.

편향과 분산이라는 개념을 이전 포스팅중에서 다룬적이 있다. 아직 잘모른다면 https://velog.io/@ljs7463/%ED%8E%B8%ED%96%A5-%EB%B6%84%EC%82%B0-%ED%8A%B8%EB%A0%88%EC%9D%B4%EB%93%9C%EC%98%A4%ED%94%84
해당 링크를 참고하면된다.

본론으로 돌아가서. 릿지회귀는 이 편향을 조금 더해주고, 분산을 줄이는 방법으로 정규화를 하는것이다. 여기서 말하는 정규화는 모델을 변형하여 과적합을 완화하여 일반화(generalization) 성능을높혀주기 위한 기법이다. 릿지회귀에는 이런역할을 하는 것이 람다의 형태로 존재한다.

람다는 값이 커질수록 회귀계수들을 0으로 수렴(기울기를 평균과 비슷하게)시키며 이것은 덜 중요한 특성의 개수를 줄이는 효과이다(과적합을 줄이는 효과), 람다가 0에 가까워 질수록 다중회귀 모델이 되므로 적정람다값을 구하는것이 일반화가 잘되는 지점을 찾는것이며 이것을 정규화 모델이라고 부른다.

람다값의 변화에 따른 변화를 시각화로 알아보자




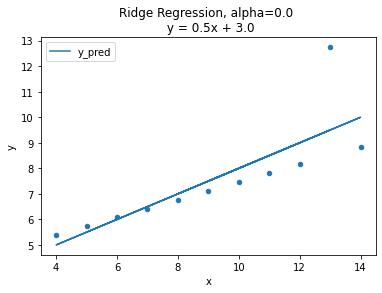
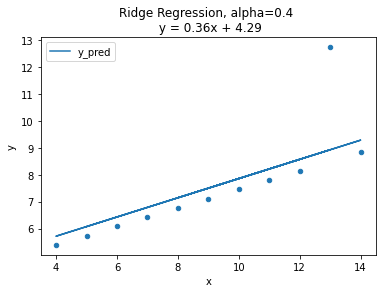
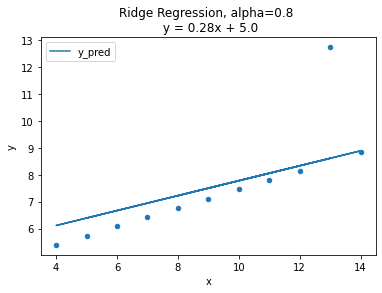
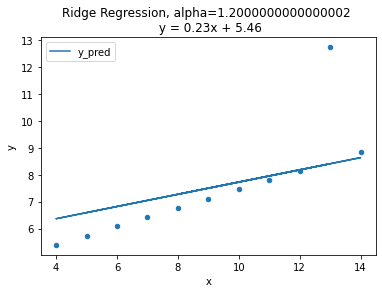
(사진출처: 코드스테이츠)

그래프에는 alpha값 즉 람다에값에 따른 기울기의 변화를 나타낸것입니다. 람다값이 커질수록 회귀계수의 값은 0에 가까워 지고 기울기는 평균기준모델에 가까워 지는 것을 볼 수 있습니다.

그렇다면 이 람다값(alpha, 패널티)을 효과적으로 구할 수 있는 방법이 필요합니다.

패널티값을 효과적으로 구하는 방법

먼저 가장 떠오르는 방법은 특별한 공식이 아닌 여러 패널티 값을 가지고 검증실험을 하는것입니다. 즉 교차검증(cross-validation)을 사용하해서 검증실험을 진행하는 것입니다.

하지만, 아직 해당 부분까지 학습을 마치지 못해서 RidgeCV를 통해서 최적의 패널티(alpha,람다)를 검증하는 방법을 알아 보겠습니다.

RidgeCV

from sklearn.linear_model import RidgeCV

alphas = [0.01, 0.05, 0.1, 0.2, 1.0, 10.0, 100.0, 1000.0]

ridge = RidgeCV(alphas=alphas, normalize=True, cv=3)
ridge.fit(ans[['x']], ans['y'])
print(ridge.alpha_)
print(ridge.best_score_)
>>>0.2
>>>0.43897...