[논문 리뷰] Beyond Masked and Unmasked: Discrete Diffusion Models via Partial Masking

논문링크

이전에 읽었는데 핵심만 짧게 작성하겠다.
추가로 이 논문은 discrete diffusion token을 여러개의 bit로 표현한다는 점에서 analog bit이라는 논문이 생각난다.

Abstract

Maksed diffusion language model은 [MASK] token을 예측함으로써 sequence를 복구하는데 좋은 성능을 보이지만 오직 [MASK] or not 2가지 token representation만 존재한다.
이때 schedule을 따라서 예측한 [MASK] token을 오픈하는 generation 과정을 진행하는데 schedule을 따라서 샘플링을 진행하기에 이전 step의 input과 현재 step의 input이 동일해서 동일한 input을 2번 처리하는 redundant computation을 반복하는 문제가 제시된다.
이 논문은 [MASK] token이냐 아니냐 즉 기존 바이너리 representation을 여러개의 bit로 쪼개서 표현함으로써 token을 구체적으로 표현하고 좀더 뛰어난 묘사를 가능하게 하였다.

MDLM 즉 masked diffusion language model은 쉽게 생각해서 multi-step bert 같은 거라고 생각하면 된다. 각 step마다 diffusion scheduling을 따라서 생성을 하는데 사실상 매 step [MASK] token 맞추기 task를 진행하기 때문
자세한 내용은 MDLM 리뷰를 작성했으니 보면 좋을 것 같다.

Introduction

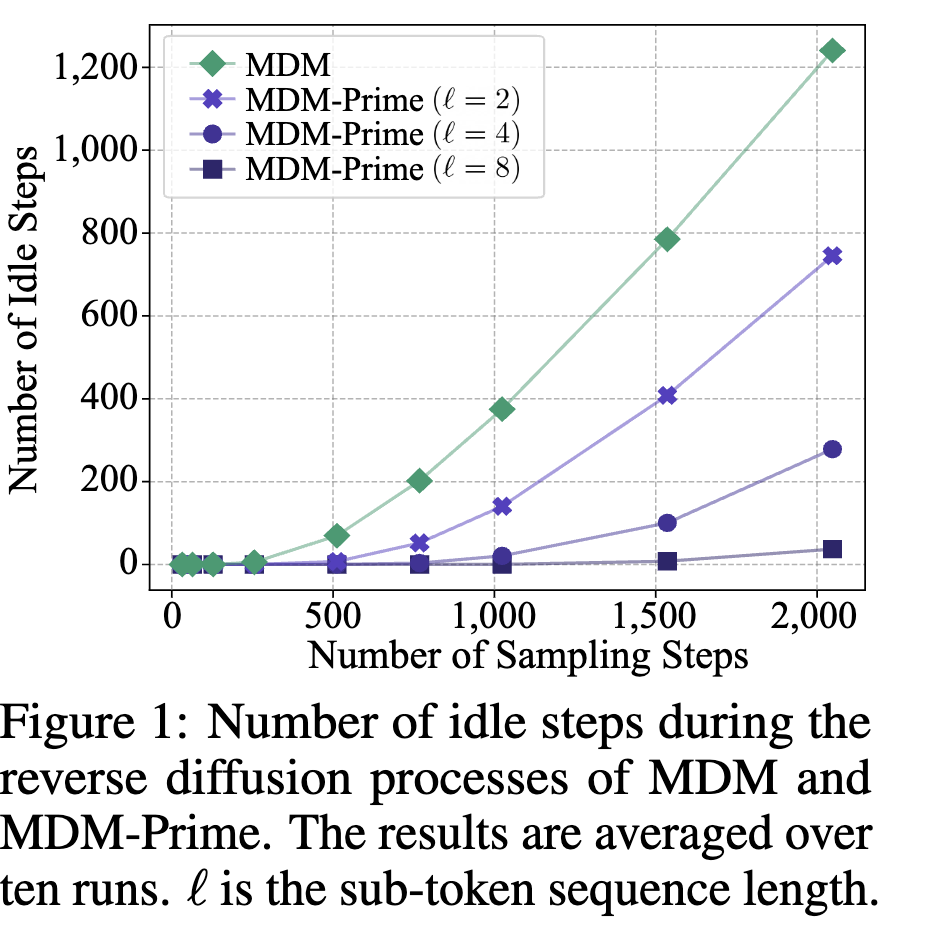위 이미지가 이 논문의 핵심인데 generation을 진행하는 도중에 schedule을 따라서 각 [MASK] token을 오픈하냐 마냐의 sampling을 진행하는데 아무것도 open되지 않아서 이전의 step의 input과 동일한 input을 처리하는 즉, idle step의 빈도를 sampling step마다 나타낸 것이다.
재미있는 부분은 1024 정도이세 거의 400번 가량의 idle step을 보이며 그 만큼 computation이 낭비된 것이다.

이 논문은 그 부분을 [MASK] token을 여러개의 bit로 쪼개서 표현함으로써 idle step을 줄이고 성능을 올렸다.

Methodology

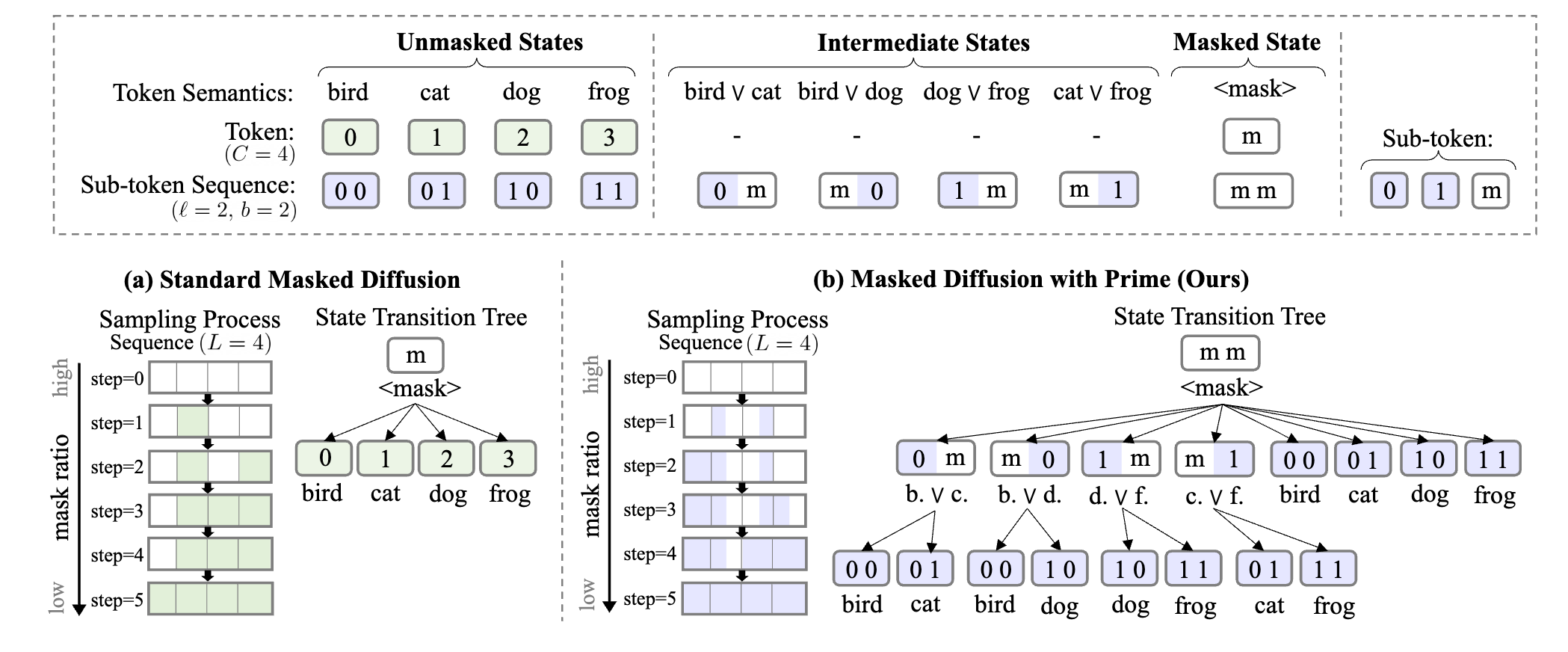
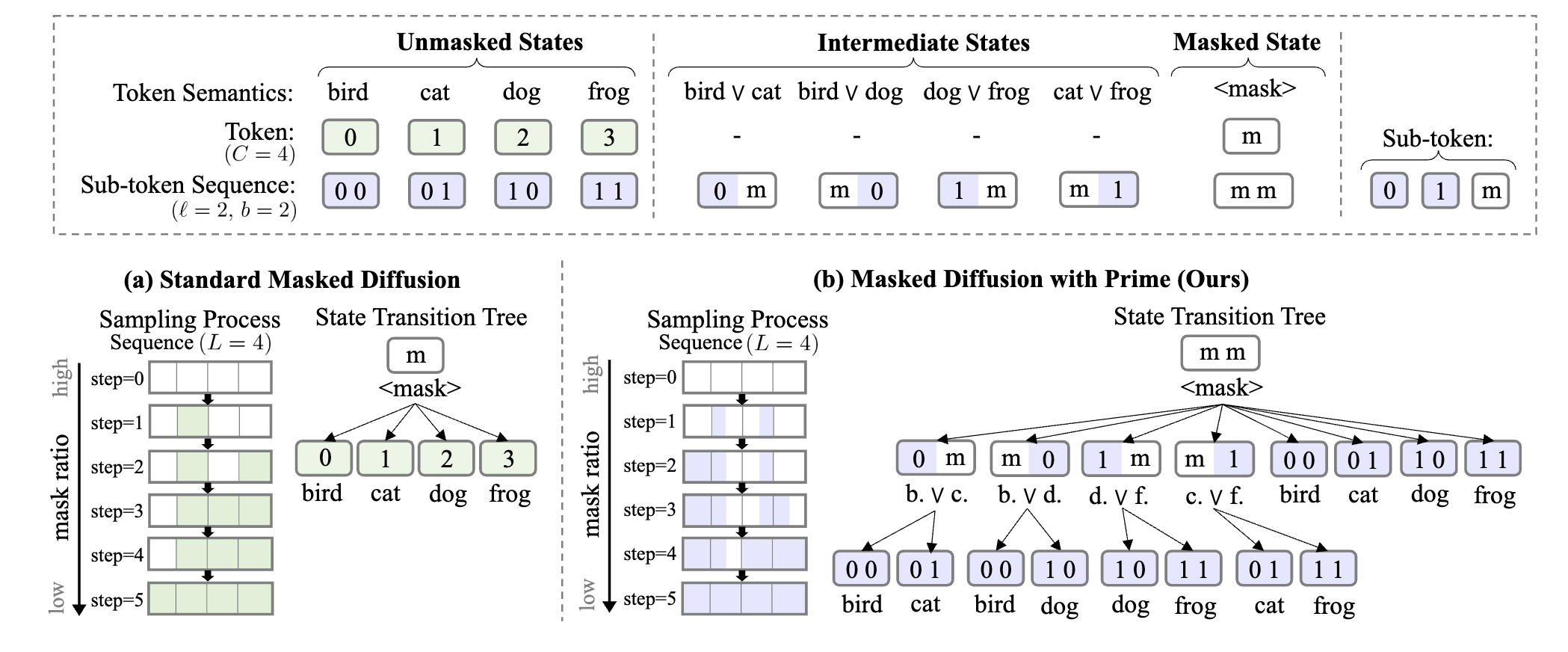
3.1 Discrete Diffusion via Partial Masking

진짜 심플하게 위 그럼처럼 (a)의 mask token을 예측하는 것에서 (b)처럼 이를 2개의 mask bit으로 쪼개서 표현 함으로써 가능한 경우의 숫자를 여러번 나눠서 표현하게 만들고 동시에 sampling schedule을 더 잘게 나눠서 진행함으로써 idle step을 줄였다.

쪼개는 bit의 크기는 $l$로 표현을 하며 $b=\sqrt[l]{C}$의 ceil로 즉 vocab을 $l$ 승으로 나눈 만큼이다.
예를 들어서 vocab의 크기가 50000이고 $l=4$ 이면 14.95... -> 각 비트는 15진수가 될 것 이다.
이때 ceil로 14.95를 15로 만듬으로 인해서 늘어나는 vocab은 뒤에서 따로 처리해준다.

3.2 Parameterization

이 부분이 좀 재밌는데 모델링을 하는 과정에서 각 bit representation을 독립적으로 model이 예측하게 할 수 있을 것이다.
ex) 1개의 token을 예측하는 경우 $p(x^{(i)}_{t-1}|\bold x_t)=\prod_l p(x^{(i),l}_{t-1}|\bold x_t)$ 대충 이렇게 1개의 token을 표현할 때 여러개의 bit를 independent하게 modeling을 할 수 있을 것인데 이러면 문제가 발생하는게 token 내부의 bit 표현 간에 dependency를 modeling을 하지 못한다.
결국 위 그림의 (a)처럼 점점 $l$이 늘어날수록 내용이 이상해진다.

그래서 bit 표현을 joint하게 표현을 진행하는데 간단하게 현재 주어진 bit 상태에서 가능한 bit 표현을 classification을 진행한다고 생각하면 된다. 이때 불가능한 경우는 확률 0%로 할당하는 식으로.
예시로 위에서 50000의 vocab의 경우 $l=4$일때 가능한 bit가 15라고 하였는데 여기에 [MASK] token을 넣으면 각 bit마다 16까지 표현이 될것이다.
그럼 $16^4$의 표현이 가능한데 여기에서 classification을 진행하고 각 bit상태에서 불가능한 경우는 없애버리면 자연스럽게 진행이 된다.

위 그림을 보면 이해가 쉽다. 현재 mmm에서는 모든게 가능하니까 다 확률이 있고 (0,m,m)은 앞이 0인 부분만 가능하고 (m,1,m)은 중간이 1인 부분만 가능하고 나머지는 다 0 이런 식이다.

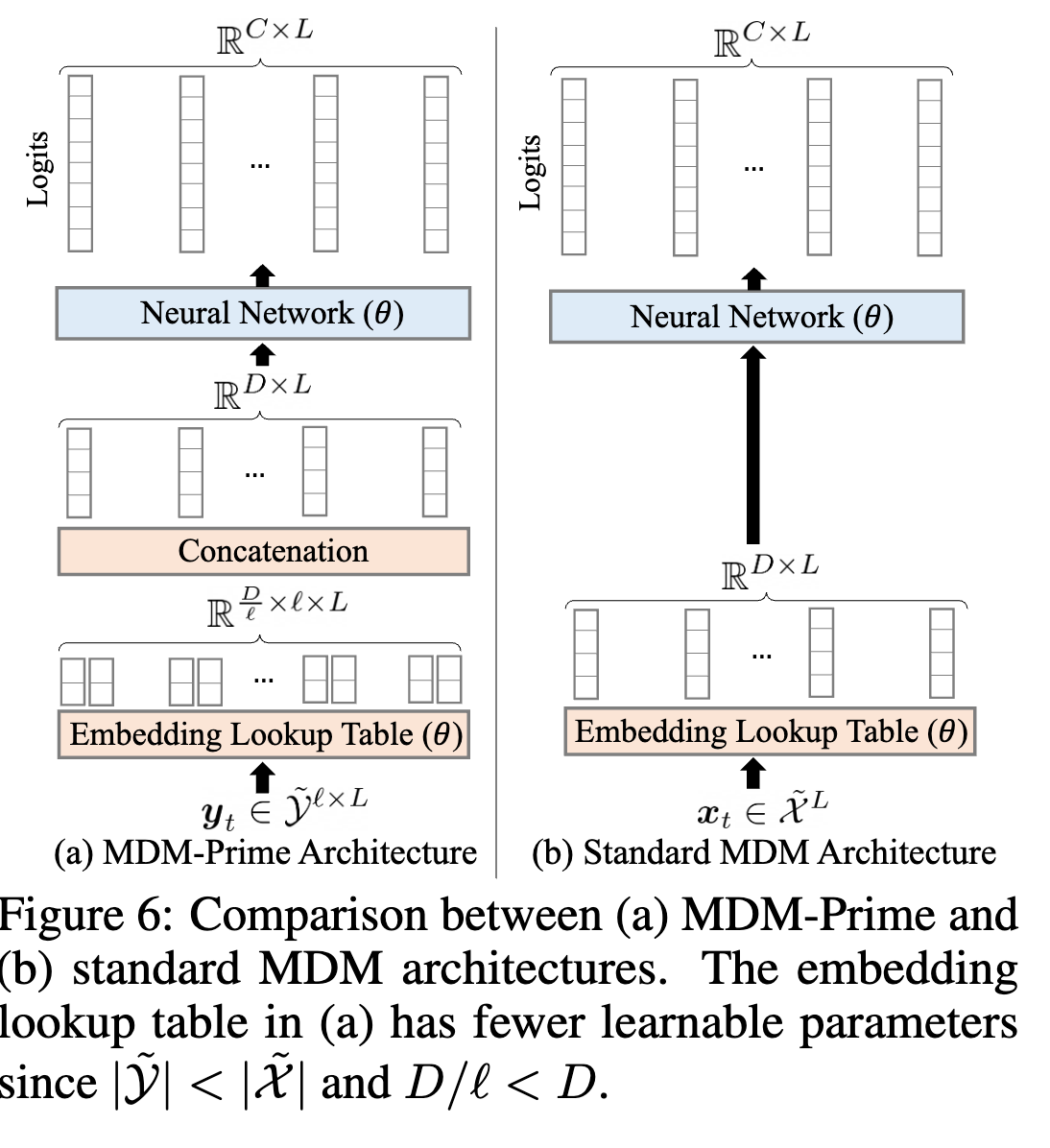위 그림은 embedding을 표현이 가능한 각 경우의 수 bit마다 따로 표현을 하면 cost가 낭비가 되니까 이를 나눠서 각 bit마다 표현을 하고 이를 붙여서 1개의 token embedding을 만든다는 내용이다.

Experiments

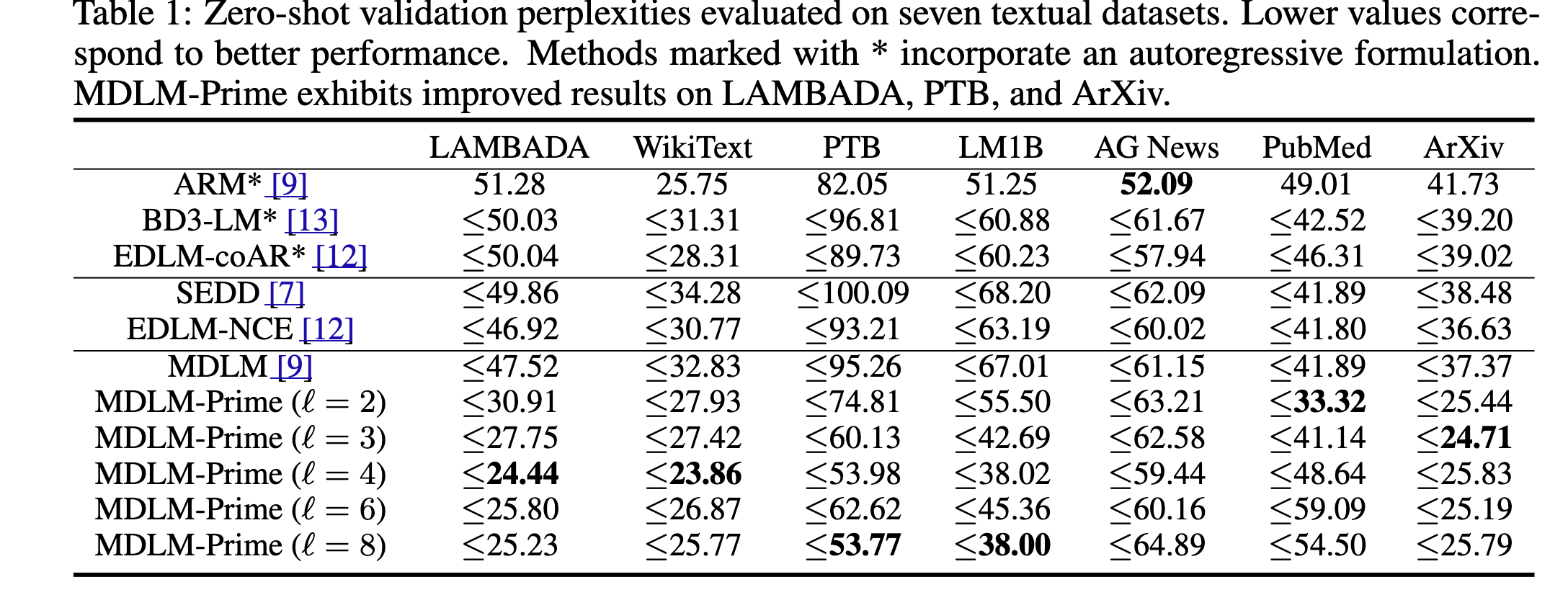
위 내용은 perplexity인데 얼마나 주어진 문장을 잘 복구할 수 있냐
즉, log-likelihood이다.
여기에서 기존의 model을 압도하는 performance를 보이는데 사실 나는 이거 납득을 못한다.
실질적으로 perplexity는 loss를 이용해서 monte carlo estimate를 진행해서 평가를 하는데
사실 얘네들이 제시하는 내용은 classification을 잘게 쪼개서 예측을 하는건데 그러면 당연히 가능한 경우의 숫자가 줄어들기에 task가 훨씬 쉬워진다.
그래서 loss가 낮게 나오는건 당연한건데 이거를 가지고 막 압도적인 performance를 냈다고 주장하는 것 같아서 납득하기 힘들다.
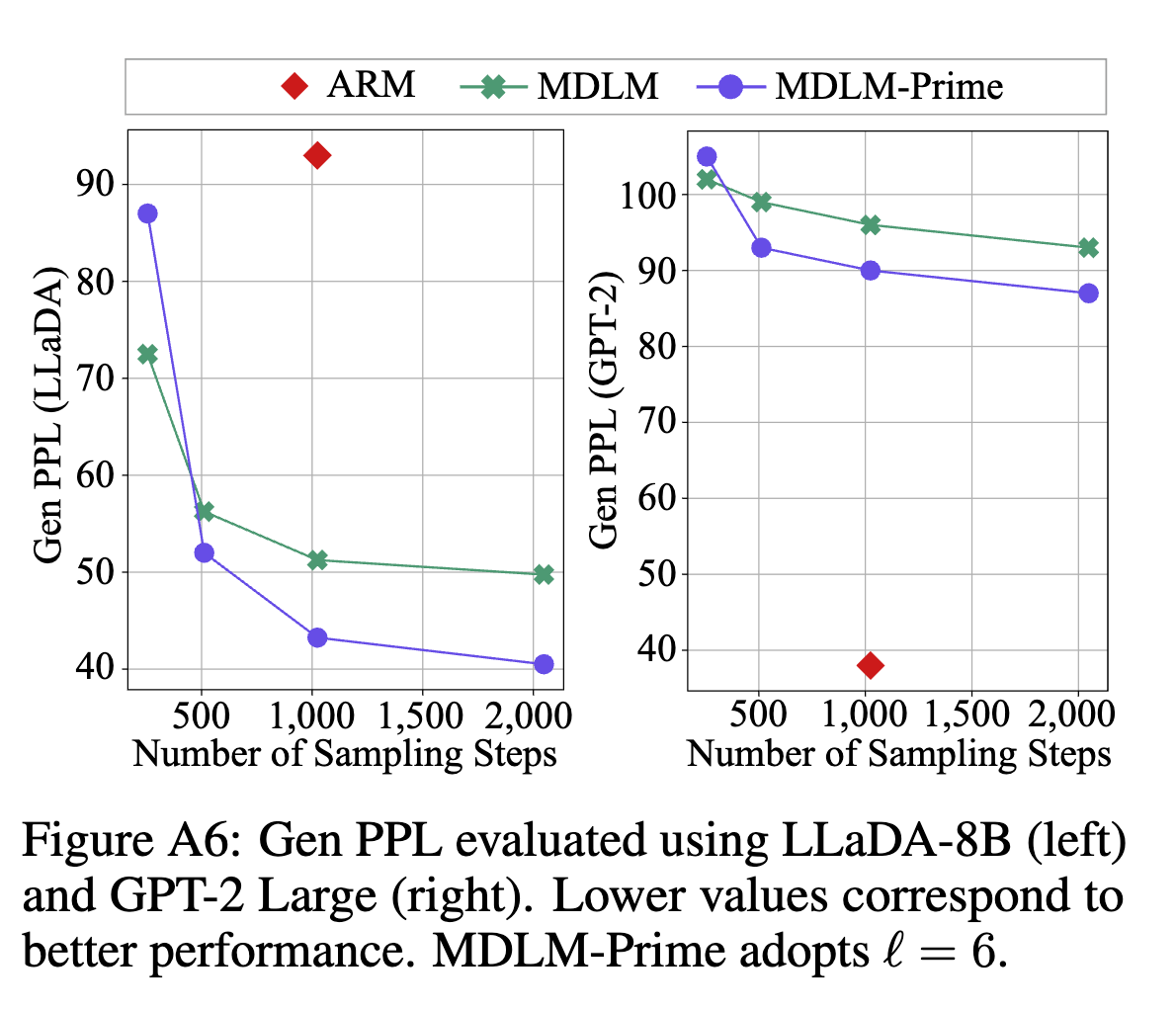실제로 위처럼 sampling으로 만든 sample의 quality를 평가하는 Genppl에서 오른쪽 그림을 보면 생성한 sample을 gpt2-large model로 ppl을 평가한 내용인데 앞서 보여준 ppl만큼 압도적인 성능 향상이 없다.
근데 저자는 이 내용을 appendix에 숨겨두었다. 본인들도 아는게 아닐까?

왼쪽 llada로 평가하는 방법은 잘 사용하지 않는다. GPT2-large가 평가하는 것을 보통 discrete diffusion model에서는 많이 사용하고 아무래도 AR의 퀄리티가 객관적으로 봤을 때 훨씬 좋기 때문이다.