[논문 리뷰 및 구현] Bootstrap Your Own Latent A New Approach to Self-Supervised Learning

pyross·2024년 8월 16일

Contrastive Learning Self-supervised Learning 구현 논문리뷰

paper

목록 보기

22/63

Abstract

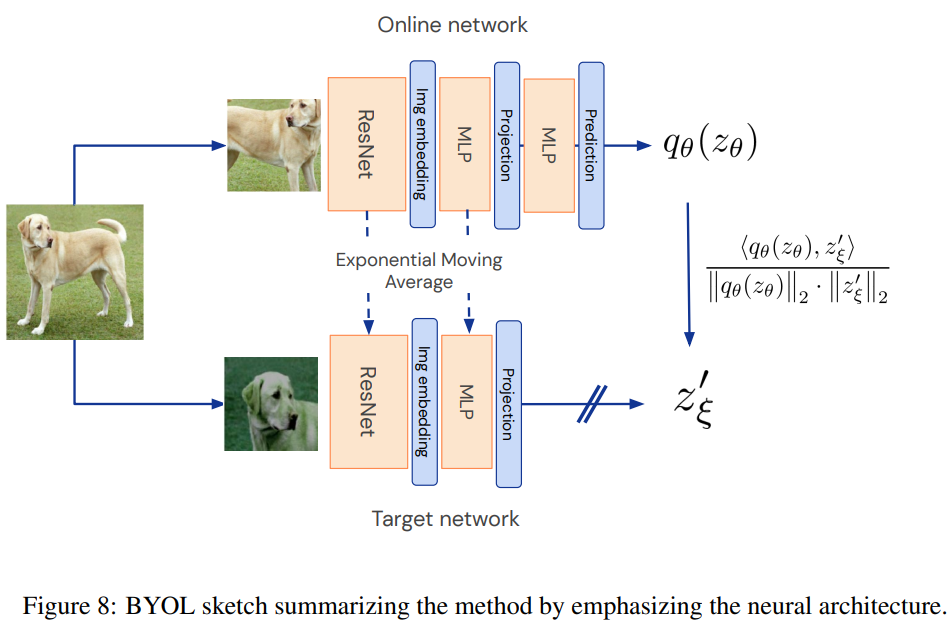
Bootstrap Your Own Latent(BYOL)를 제시
이전의 contrastive learning과 같이 2개의 network를 사용한다.
1개는 target, 1개는 online 이들은 서로 배운다.
online network는 target network와 서로 다른 data augmentation을 거친 이미지를 가지고 representation을 예측한다.
이때 target network는 MOCO와 같이 매우 천천히 업데이트가 이루어진다.
여기에서 BYOL은 positive sample만 사용해서 학습을 진행한다.

1. Introduction

최근 contrastive learning의 방법은 이미지의 representation을 positive 끼리는 가깝게 negative와는 멀게 학습을 한다.
이때 그 성능은 augmentation과 negative smaple의 선택에 따라 매우 크게 달라진다.

BYOL은 negative sample없이 좋은 성능을 얻었다.
또한 BYOL은 augmentation에도 robust하다.(이는 negative에 의존하지 않기 때문으로 추측)

BYOL은 online network가 targe network의 representation을 예측하는 식으로 진행이 되는데 예상되는 몇가지 문제점이 있다.
모든 이미지에 대해서 동일한 vector을 만들면 무조건 100점을 만드는 등의 shortcut이 존재하는 것이다.
그러나 다음 2가지 방법을 통해 문제를 피할 수 있다고 생각한다.
1. online-network에 추가 predictor 달기
2. online-network param으로 target network가 느리게 이동함으로 online network는 더 많은 정보를 담을 수 있다.

3. Method

기존의 contrastive learning은 2개의 augmentation을 가한 view를 통해 서로의 이미지를 다른 1개로 예측하는 방법이 있었는데 이는 표현이 붕괴될 위험이 존재한다. (동일한 representation은 항상 서로를 예측할 수 있기에 표현이 똑같아지는 것이 가능)
이를 통해 예측이 아니라 구분으로 문제를 바꾸고 positive와는 가깝게 negative와는 멀게 학습을 하는 식으로 붕괴를 막았다.
이 논문의 저자는 negative가 collapse를 막는데 필수적인가? 에 의문을 던진다.

붕괴를 막기 가장 직관적인 방법은 fix된 target network이다.
그러나 이는 좋은 representation을 보여주지 않았다.
하지만 이 과정에서 얻게된 표현은 최소한 fix된 표현보다는 더 좋았다.
이게 BYOL의 핵심 아이디어이다.
위 과정(점점 param이 느리게 움직이는 target netrowk로 학습 -> negative sample 없이 붕괴를 피하고 성능을 늘림)

3.1 Description of BYOL

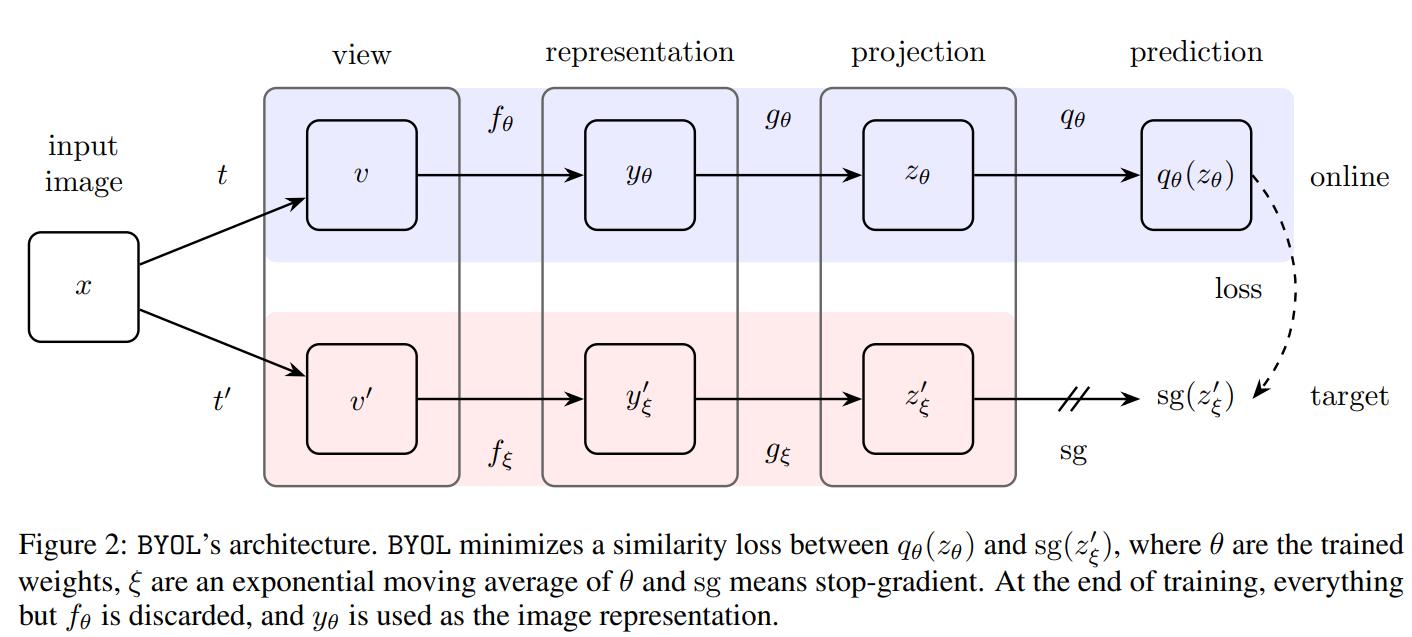network는 위와 같이 구성이 된다.(sg는 stop gradient)
이전과 다른 점은 online-network에 prediction layer가 추가로 달렸다는 것이다.
target network의 weight는 $\xi$ 이고 다음과 같이 업데이트 된다.
$\xi=\tau\xi+(1-\tau)\theta$
이때 prediction에 사용하는 $q_\theta(z_\theta)$ 와 $z'_\xi$ 는 l2_norm을 적용한다.

이렇게 나온 loss는 다음과 같다.
$\mathcal{L}_{\theta, \xi} \triangleq \left\lVert \overline{q_\theta(z_\theta)} - \overline{z'_\xi} \right\rVert_2^2 = 2 - 2 \cdot \frac{\left\langle q_\theta(z_\theta), z'_\xi \right\rangle}{\left\lVert q_\theta(z_\theta) \right\rVert_2 \cdot \left\lVert z'_\xi \right\rVert_2}$

여기에서 밑에 있는 2는 L2 norm을 나타내는 것이다. 위의 2는 제곱즉 위 식은 유클리디안 거리를 나타낸다.(벡터 차이의 l2 norm의 제곱)

이때 input $v,v'$ 을 바꿔서 한번 더 계산해준다.
$\mathcal{L}^{BYOL}_{\theta,\xi}=\mathcal{L}_{\theta,\xi}+\tilde\mathcal{L}_{\xi,\theta}$

이후 weight는 다음과 같이 업데이트 된다.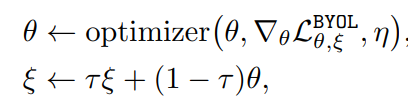

3.2 Intuitions on BYOL’s behavior

BYOL은 collapse를 막는 negative sample이 없다.
그렇기 때문에 무작정 loss가 minimum으로 수렴하게 진행되어서 collapse(둘다 고정된 representation을 만드는 경우)가 발생할 것 같지만 $\xi$ 의 param은 $\nabla_{\xi}\mathcal{L}^{BYOL}_{\theta,\xi}$ 의 방향으로 업데이트 되지 않기 때문에 collapse가 발생할 확률은 거의 없을 것이라 추측한다.
이는 GAN에서 discriminator와 generator의 param을 동시에 고려해서 loss가 최소화 되는 경우가 없는 것처럼 여기 역시 둘다 동시에 loss를 최소화되게 만드는 경우가 없기 때문에 collapse가 발생하지 않는다고 가정한다.

이때 논문의 저자들은 여전히 collapse가 발생할 수 있음을 인정하지만 아직까지 그런 경우가 발견되지 않았다고 함
그리고 추가로 그러한 경우가 있어도 불안정하다고 한다.

여기는 collapse가 불안정하다는 증명인데 이해가 안되어서 이것저것 찾아보니 실제로도 설명이 이상해서 그냥 다른 논문을 보는 것이 좋다고 한다 그래도 일단 나름 적어보겠다.

만약 q가 최적일때 아래를 만족한다.
$q^\star \triangleq \arg \min_{q} \mathbb{E} \left[\left\lVert q(z_\theta) - z'_\xi \right\rVert_2^2 \right], \quad \text{where} \quad q^\star(z_\theta) = \mathbb{E} \left[z'_\xi \mid z_\theta \right]$

살짝 설명하자면 $q^\star$ 는 loss를 최저로 줄이는 $q$ 이고 오른쪽의 의미는 $q^\star$ 는 $z_\theta$ 일때 $z_\xi'$ 의 기댓값 이라는 의미이다. 즉 조건부 기대값이다. 즉 $z_\theta$ 가 주어졌을 때 $z'_\xi$ 와 가장 관련성이 높은 값을 예측하는 것이다.

이 식의 gradient는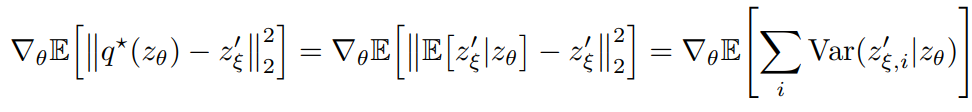이렇게 도출이 되는데 평균-값의 제곱은 분산이니까 오른쪽 처럼 된다.
이때 일반적인 상황에서 $Var(X|Y,Z)\le VAR(X|Y)$ 이 식을 보통 만족하는데(정보가 더 많기 때문에 variance가 적음) $X$ 를 target, $Y$ 를 prediction, $Z$ 를 train variance일 때 만약 $z_\theta=c$ 가 된다면 정보가 더 줄어들기 때문에 $Var$ 이 더 커져서 $Var(z_\xi' |z_\theta)\leq Var(z'_\xi|c)$ 가 되어서 더 불안정해진다는 것이다.

4. Experimental evaluation

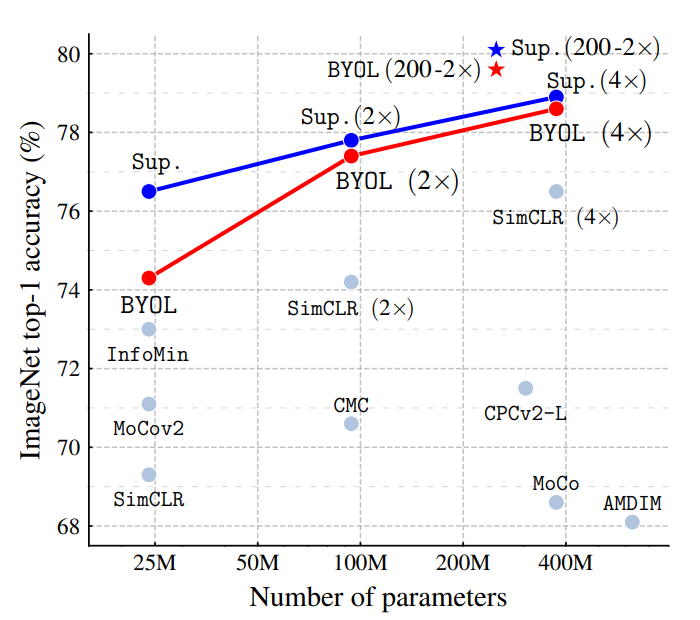
기존의 linear evaluation
imageNet dataset에서 다른 방법론보다 매우 좋은 성능을 보임
semi-supervised(조금의 train data로 학습을 더함 1%, 10%)

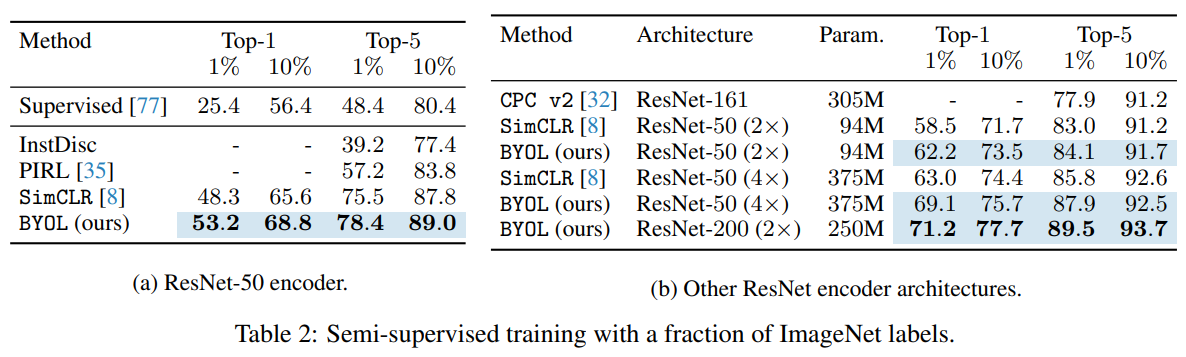
5. Building intuitions with ablations

이것저것 테스트

batch size, transform set
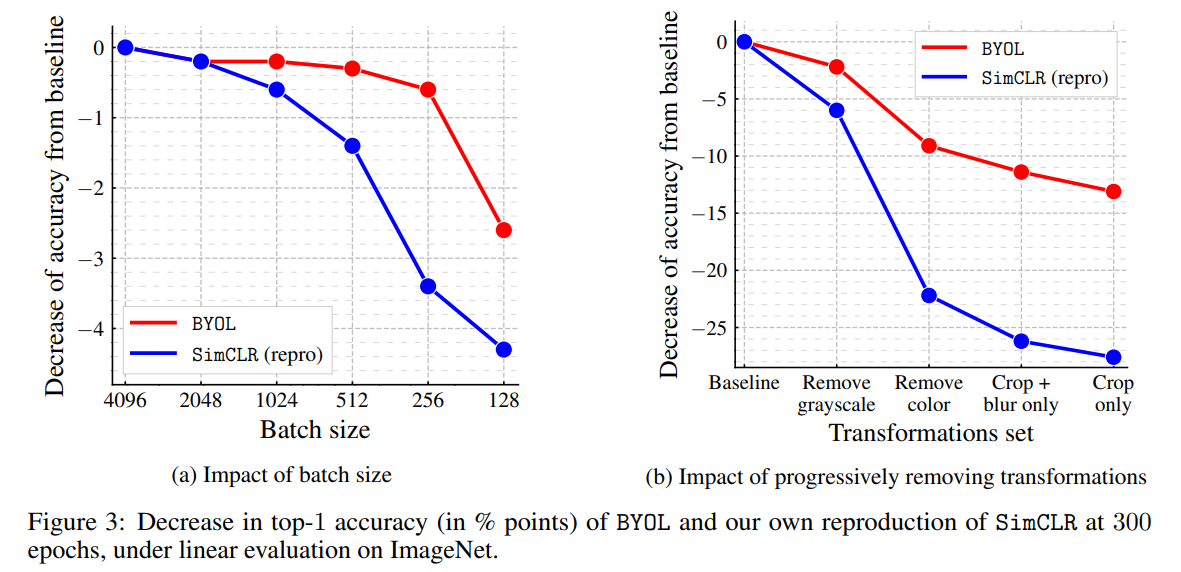negative sample에 의존하지 않아서 batch size가 작아져도 더 강건한 모습

두번째는 augmentation을 바꿨을 때인데 기존의 contrastive learning은 단순하게 positive sample과는 가깝게, negative와는 멀게 학습하기에 short cut이 생기기 쉬움(color histogram으로 비슷한 분포를 가진 positive sample 예측이 가능 등)
그러나 byol은 target network의 정보를 online network에 담는 식으로 진행이 됨. 즉 short cut이 발생하기 상대적으로 더 어려움 그렇기 때문에 augmentation에 상대적으로 매우 강건함.(같은 이미지 분포를 가져도 예측을 더 정확하게 만들기 위해 특징을 계속 가져옴)
bootstraping $\tau$ 테스트
Ablation to contrastive methods
즉 simclr와 contrastive 학습 방법에서 무슨 부분에서 좋은 성능이 오는지 테스트
기존 simclr의 loss
$\ell_{i,j} = -\log \frac{\exp(\text{sim}(z_i, z_j)/\tau)}{\sum_{k=1}^{2N} \mathbb{1}_{[k \neq i]} \exp(\text{sim}(z_i, z_k)/\tau)}$ 에서
log를 ln으로보고 윗 부분과 아랫 부분을 분리하면 아래와 같은 식 완성
$\text{InfoNCE}_{\theta}^{\alpha, \beta} \triangleq \frac{2}{B} \sum_{i=1}^{B} S_{\theta}(v_i, v'_i) - \beta \cdot \frac{2\alpha}{B} \sum_{i=1}^{B} \ln \left( \sum_{j \neq i} \exp \frac{S_{\theta}(v_i, v_j)}{\alpha} + \sum_{j} \exp \frac{S_{\theta}(v_i, v'_j)}{\alpha} \right)$
되게 어려워 보이지만 그냥 simclr의 loss를 윗 부분과 아랫 부분을 분리하고 2를 곱하고 뒷 부분에 $\beta$ 를 곱해서 simclr loss와 BYOL의 loss를 왔다갔다 할 수 있게 만든 것.
여기에서 $\beta=0$ 이면( $\alpha$ 는 temperature) BYOL의 loss와 가까워짐 $S_\theta$ 는 cos sim이기 때문에
$2-2*S_\theta(v_i,v_j)$ 가 바로 BYOL의 loss이기 때문.
반면 $\beta=1$ 이면 simclr의 loss
테스트 결과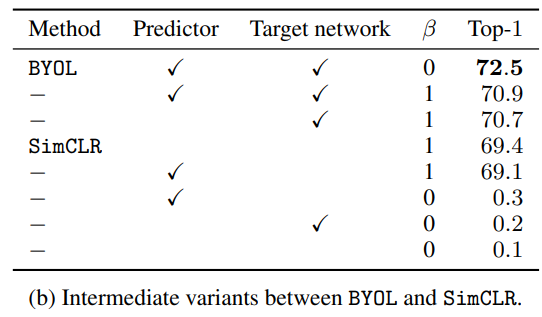이제 보면 BYOL은 predictor가 있고 $\beta=0$ 일때 성능이 가장 좋았다.
simclr은 역시 기본 상태가 성능이 가장 좋았다.
이때 simclr에 그냥 target network를 넣는 것은 성능을 올려줌(MoCo)
simclr에 BYOL의 loss를 넣으면 학습이 붕괴되어서 성능이 매우 떨어짐

Conclusion

기존의 infoNCE를 이용하여 positive, negative 쌍을 이용하는 contrastive learning의 방법과는 다른 방법으로 positive 만으로 학습을 잘 할 수 있음을 보여준 논문

구현

class BYOL(Framework):
    def __init__(self, device, args, dim=128, m=0.996):
        self.m = m
        model = load_model(args.model, class_num=dim)
        super().__init__(model, criterion=nn.CrossEntropyLoss(), device=device)

        dim_mlp = self.encoder.out.weight.shape[1]
        hidden_dim = 2048
        self.encoder.out = nn.Sequential(
            nn.Linear(dim_mlp, hidden_dim),
            nn.BatchNorm1d(hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.BatchNorm1d(hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.BatchNorm1d(hidden_dim),
            nn.ReLU(),
        )
        self.predictor = nn.Sequential(
            nn.Linear(hidden_dim, hidden_dim // 4),
            nn.BatchNorm1d(hidden_dim // 4),
            nn.ReLU(),
            nn.Linear(hidden_dim // 4, hidden_dim),
        )
        self.encoder = self.encoder.to(device)
        self.target_encoder = copy.deepcopy(self.encoder).to(device)
        self.predictor = self.predictor.to(device)

        for param_q, param_k in zip(self.encoder.parameters(), self.target_encoder.parameters()):
            param_k.data.copy_(param_q.data)
            param_k.requires_grad = False

    def forward(self, batch):
        x1, x2 = batch[0][0].to(self.device), batch[0][1].to(self.device)
        # (batch, 3, 32, 32)
        self.update_key_()

        p1 = self.predictor(self.encoder(x1))
        z2 = self.target_encoder(x2)

        p2 = self.predictor(self.encoder(x2))
        z1 = self.target_encoder(x1)

        loss = self.loss_(p1, z2.detach()) + self.loss_(p2, z1.detach())
        return loss.mean()

    def loss_(self, x1, x2):
        x1 = F.normalize(x1, dim=-1, p=2)
        x2 = F.normalize(x2, dim=-1, p=2)
        return 2 - 2 * (x1 * x2).sum(dim=-1)

    def update_key_(self):
        for param_q, param_k in zip(self.encoder.parameters(), self.target_encoder.parameters()):
            param_k.data = param_k.data * self.m + param_q.data * (1. - self.m)