[논문 리뷰 및 구현]Exploring Simple Siamese Representation Learning

pyross·2024년 8월 18일

Contrastive Learning Self-supervised Learning 구현 논문리뷰

paper

목록 보기

23/63

Abstract

contrastive learning에서 쓰이는 샴(2개)의 네트워크는 일반적인 구조로 정착이 되었다.
이는 2개의 view의 유사성을 최대화 하는 구조인데 collapse(constant representation)을 막기 위해 다양한 방법이 사용이 됨
이 논문은

negative sample
large batch
momentum encoder

등을 사용하지 않고 stop-gradient를 이용하여 이러한 collapse를 막고 학습을 하는 방법을 제시함.

1. Introduction

최근 샴의 network를 이용하여 1개의 input을 2개의 view로 구성하고 비교해서 유사성을 최대화하는 방식이 많이 사용이 됨.

그러나 이러한 방법은 collapse(constant representation 등)의 문제를 가지고 있음.
view 2개가 똑같은 representation을 가지면 항상 loss가 0이기 때문.
이를 막기 위한 다양한 방법이 존재

simclr: positive sample을 negative sample과 비교하는 식으로 문제를 정의(negative sample이 constant representation을 막아줌)
SaAV: clustering으로 막음
BYOL: positive pair만 쓰지만 momentum encoder를 이용하여 collapse를 막음

이 논문은 BYOL처럼 positive pair만 쓰지만 stop-gradient를 이용하면 momentum encoder를 사용하지 않고도 학습이 가능하다는 것을 보여줌
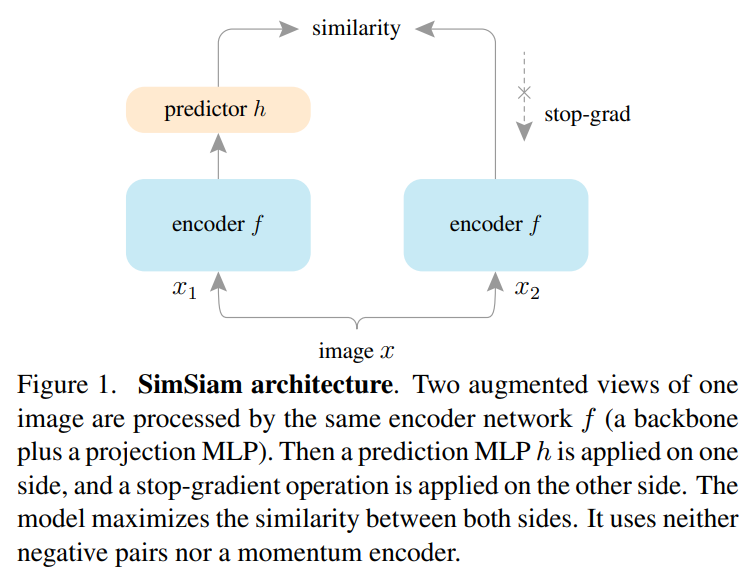stop-gradient가 매우 중요한데 이는 각각의 문제가 다른 최적화 문제라는 것을 보여준다.

또한 샴의 network는 inductive bias를 가지고 있음을 보여주는데
이는 같은 concept의 다른 view는 동일한 output을 가지고 있어야 함을 보여준다.
cnn과 유사하게 translation-invariance를 가진다고 볼 수 있다.

3. Method

위 그림과 같이 구성이 되는데 encoder $f$ 는 resnet과 같은 backbone 모델과 projection MLP로 구성이 된다.
이후 1개의 view로 다른 것을 예측하게 하는 prediction MLP $h$ 가 붙어있다.

이때 BYOL의 loss와 조금 다른데 우선
$\mathcal{D}(p_1,z_2)=-\frac{p_1}{||p_1||_2}\cdot \frac{z_2}{||z_2||_2}$ 들로 구성이 되는데 이전의 BYOL의 loss에서 2가 없는 상황이다.
이는 negative cosine sim이다.

즉 cos sim은 유사도이기 때문에 negative sim을 줄이려면 유사도를 더 늘려야 하기 때문에 두 벡터를 더 가깝게 만들 수 있다.

이후 loss는 2개의 view를 서로 예측할 수 있게 해주기 위해 다음과 같이 구상한다.
$\mathcal{L}=\frac{1}{2}\mathcal{D}(p_1,z_2)+\frac{1}{2}\mathcal{D}(p_2,z_1)$ 가능한 최소의 값은 -1이다.

setting

projection head는 layer 3개의 MLP로 구성이 되어 있으며 각각 BN이 적용되어 있고 output layer를 제외하고 ReLU가 붙어있다. hidden-dim은 2048이다. (linear-BN-ReLU)*3
prediction head은 2개의 layer로 구성이 되어있으며 output layer에는 BN과 ReLU가 모두 적용이 되지 않고 첫번째 layer에만 적용이 되어있다. input과 output의 dim은 2048이고 hidden dim은 512이다.
(linear-BN-ReLU-linear)

4. Empirical Study

4.1 Stop-gradient

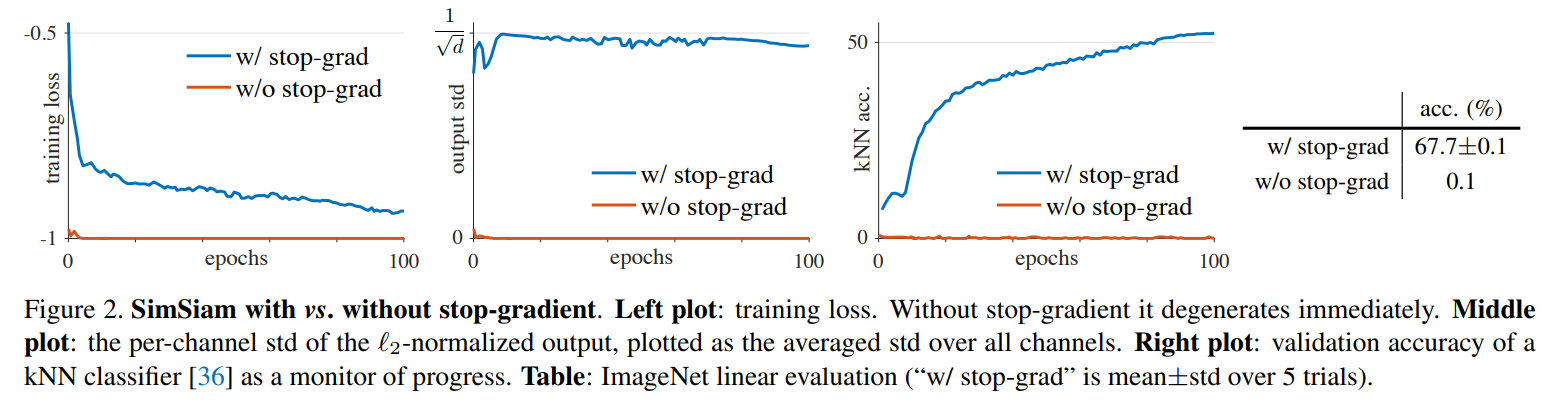stop-gradient를 사용하지 않으면 바로 collapse 즉 constant vector를 만들어내게 된다.
위 그림을 보면 loss가 바로 최저인 -1로 가지만 KNN 정확도가 거의 0이고 std 즉 표준편차가 0이다.
반면에 stop-gradient를 사용한 학습은 정규화가 되어서 정상적인 표준편차인 $\frac{1}{\sqrt{d}}$ 가 나오게 되었다.

$z_i'=\frac{z_i}{(\sum_{j=1}^dz_j^2)^{\frac{1}{2}}}$ 가 되고 $z_j\sim \mathcal{N}(0,1)$ 을 따르게 되기에 $std[z_i]\sim \frac{1}{\sqrt d}$ 가 된 것이다.

4.2 Predictor

결과는 위와 같은데
1. Predictor $h$ 를 지우면 성능이 0.1% 즉 고장이 난다.
loss가 $\mathcal{L}=\frac{1}{2}\mathcal{D}(p_1,z_2)+\frac{1}{2}\mathcal{D}(p_2,z_1)$ 이렇게 구성이 되는데
prediction이 없기 때문에
결국 loss가 $\frac{1}{2}\mathcal{D}(z_1,stopgrad(z_2))+\frac{1}{2}\mathcal{D}(z_2,stopgrad(z_1))$ 가 되기 때문에 양쪽 어디로 가든지 동일하기에 stop-gradient가 의미가 없어진다.
그냥 $\frac{1}{2}\mathcal{D}(z_1,z_2)$ 의 방향으로 학습이 진행되는 것과 동일해진다.
즉 prediction이 있음으로써 stop-gradient가 의미가 있다.

이때 추가 실험으로 $\mathcal{D}(z_1,stopgrad(z_2))$ 1개만 사용해서 비대칭 loss를 적용했을 때에도 prediction layer가 없으면 collapse가 발생했다고 했다.
즉 prediction layer가 있는 것 자체만으로 좋은 효과를 준다.

prediction layer를 random한 값으로 고정해도 정확도가 매우 낮게 고장난다. 이는 collapse는 아니다. 그냥 학습이 수렴하지 않는 것이다. 결국 prediction layer $h$ 는 represnetation에 적응이 되게 학습이 되어야 한다.
prediction layer를 높은 lr을 주는 것도 좋은 성능을 보임
즉 lr을 높게 줌으로써 최신 representation에 잘 학습할 수 있도록 해주는게 성능을 상승시킬 수 있음을 보여줌.

4.3 Batch Size

batch size에 강건하다. 오히려 매우 커지면 평범한 딥러닝 학습과 비슷하게 성능이 떨어지는 것을 보여줌.

4.4 Batch Normalization

BN을 어떻게 넣는지의 실험은데
MLP에는 모두 넣고 prediction에는 output layer에는 넣지 않는 것이 좋은 성능을 보임.
output layer에 넣는 것의 문제는 collapse가 아니라 학습이 불안정해졌다는 것이다.

4.5 Similarity Function

위에서 사용한 $-\text{cossim}$ 말고 cross entropy로도 loss를 적용할 수 있다고 한다.
$\mathcal{D}(p_1,z_2)=-\text{softmax}(z_2)\cdot \text{log softmax}(p_1)$ 이때 softmax는 channel_dim으로 적용이 된다. 즉 $d$ 차원의 category 확률과 비슷하다.

cross_entropy는 $-p_1\cdot \log(p_2)$ 에서 $p_1$ 과 $p_2$ 가 같은 확률을 가지면 최소가 된다.
즉 $z_2$ 의 각 vector 확률과 $p_1$ 의 각 vector의 각 확률이 같게 되면 최소의 loss가 되기 때문에 두 벡터가 같아지게 학습이 진행된다.

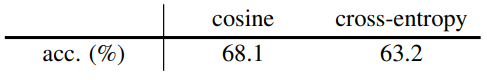이렇게 loss를 바꾸면 성능이 더 떨어졌다.
이때 cross-entropy도 collapse 없이 잘 학습이 되었다.
즉 loss는 collapse와 무관하다.

4.6 Symmetrization

$\mathcal{L}=\frac{1}{2}\mathcal{D}(p_1,z_2)+\frac{1}{2}\mathcal{D}(p_2,z_1)$ 으로 구성된 loss를 1개만 써서 asym으로 만들고 2배를 곱해보는 식으로 진행을 하였는데
sym이 더 성능이 좋았다. 1번의 view 비교를 더 할 수 있기 때문으로 생각한다.
실제로 asym을 2배 하는 것으로 어느정도 보정이 가능하다.

5. Hypothesis

5.1 Formulation

논문의 저자들은 Simsiam이 Expectation-maximization 알고리즘을 수행한다고 본다.
즉 내부에 2개의 variable set이 존재하고 2개의 sub-problem을 풂으로써 학습한다고 본다.
이때 stop-gradient는 variable-set을 추가하는 것으로 볼 수 있다.
이때 loss를 다음과 같이 표현할 수 있다.
$\mathcal{L}(\theta, \eta) = \mathbb{E}_{x, \mathcal{T}} \left[ \left\lVert \mathcal{F}_\theta (\mathcal{T}(x)) - \eta_x \right\rVert_2^2 \right]$
$\eta$ 는 stop gradient로 표현된 또다른 set of variable이고 $\mathbb{E}$ 는 기댓값이다.
$\mathcal{T}$ 는 augmenation이다.

이 loss일 때 풀어야하는 문제를 다음과 같이 바꿀 수 있다.
$\underset{\theta,\eta}{\min} \mathcal{L}(\theta,\eta)$ 즉 둘 사이의 loss로 표현할 수 있다.
이는 k-means clustering과 유사하다고 생각할 수 있다!
$\theta$ 는 center이고 encoder의 learnable param이다. $\eta_x$ 는 $x$ 에 할당되어있는 벡터이다.

$\theta^t \gets \arg\min_{\theta} \, \mathcal{L}(\theta, \eta^{t-1})$
$\eta^t \gets \arg\min_{\eta} \, \mathcal{L}(\theta^t, \eta)$
위를 토대로 2개의 sub problem을 이렇게 구성할 수 있다.

Solving for $\theta$ : stop-gradient로 $\eta$ 를 propagation 하지 않기에 $\theta$ 를 푸는 것으로 생각 가능하다.
Solving for $\eta$ : loss를 아래와 같이 표현했을 때
$\mathcal{L}(\theta, \eta) = \mathbb{E}_{x, \mathcal{T}} \left[ \left\lVert \mathcal{F}_\theta (\mathcal{T}(x)) - \eta_x \right\rVert_2^2 \right]$ 각 sample x에서 나온 $\eta_x$ 에 따라서 문제를 푸는데 예측 값의 평균을 $\eta_x$ 에 가깝게 만들도록 학습하게 된다.
결국 이는 $\eta^t_x \leftarrow \mathbb{E}_\mathcal{T}[\mathcal{F}_{\theta^t} (\mathcal{T}(x))]$ 로 표현할 수 있다.

One-step alternation.

$\eta^t_x \leftarrow \mathbb{E}_\mathcal{T}[\mathcal{F}_{\theta^t} (\mathcal{T}(x))]$ 에서 transform $\mathcal{T}$ 를 1번만 적용하고 다시 안바꾼다고 치고 $\mathcal{T}'$ 으로 근사를 하면
$\eta^t_x \leftarrow \mathcal{F}_{\theta^t} (\mathcal{T}'(x))$ 로 표현할 수 있다.
이를 토대로
$\theta^{t+1}\leftarrow \underset{\theta}{\arg\min} \mathbb{E}_{x, \mathcal{T}} \left[ \left\lVert \mathcal{F}_\theta (\mathcal{T}(x)) - \mathcal{F}_{\theta^t} (\mathcal{T}'(x)) \right\rVert_2^2 \right]$ 로 근사해서 표현할 수 있다.
$\theta^t$ 는 sub-problem에서 constant취급하고 $\mathcal{T}'$ 는 another view이다.

Predictor

위 수식들은 predictor $h$ 가 없는 상태이다.
원래 loss는 $\mathbb{E}_{z} \left[ \left\lVert h (z_1) - z_2 \right\rVert_2^2 \right]$ 이 수식을 최소화 하는 것인데

이때 $h(z_1)=\mathbb{E}_z[z_2]=\mathbb{E}_\mathcal{T}[f(\mathcal{T}(x))]$ 로 된다.
즉 h는 transform의 분포를 근사해서 $z_2$ 와 비슷하게 만들어준다.
이전에 위의 식에서 1개의 sampling 하는 식으로 근사하는 것과 비슷한 역할을 함.

즉 transform에 따른 차이를 줄여서 정확한 비교를 가능하게 만들어줌

Symmetrization

지금까지의 내용은 1개의 prediction view와 1개의 target view를 비교하는 식이다.
그러나 실제로는 2개를 바꾸면서 2번 계산한다.
이를 통해 위에서 transform의 근사 $\mathcal{T}$ 를 predictor이 학습한다고 하였는데 이를 2번 학습하게 되면서 dense하게 근사할 수 있다고 생각한다.

5.2 Proof of concept

위와 같이 가설을 세웠으면 실험으로 증명해봐야 한다.

Multi-step alternation.

위 식에는 sub-problem이 1개의 step에 대해서 왔다갔다 해결이 된다고 생각을 하였지만 multiple step도 동작해야 한다.
$\theta^t \gets \arg\min_{\theta} \, \mathcal{L}(\theta, \eta^{t-1})$
$\eta^t \gets \arg\min_{\eta} \, \mathcal{L}(\theta^t, \eta)$
위 식에서 t를 t+k로 바꾸는 식

짧게 $\theta$ 의 업데이트 주기를 변경한 것이다.

이때
$\eta^t_x \leftarrow \mathcal{F}_{\theta^t} (\mathcal{T}'(x))$ 에 필요한 모든 $\eta_x$ 는 미리 계산해서 cache에 넣어두었다고 한다.

간단하게 1개의 sample x가 있을 때
10-step의 경우 $\eta_x$ 를 미리 10개 만들어두고 1개씩 각각 prediction을 하는 방식으로 진행을 하고 $\theta$ 의 업데이트를 진행한 것으로 생각된다.

이러한 방법으로 collapse가 발생하지 않았고 심지어 10, 100-step은 더 좋은 성능을 보였음.

Expectation over augmentations.

이전에 predictor $h$ 의 기능은 $\mathbb{E}_\mathcal{T}$ 를 근사하는 것이라고 생각하였다.
이를 대체할 방법으로
$\eta_x^t \gets m \ast \eta_x^{t-1} + (1 - m) \ast \mathcal{F}_{\theta^t}(\mathcal{T}'(x))$
으로 $\eta$ 를 업데이트 하게 된다면 $h$ 를 사용하지 않고도 $\eta$ 를 바꾸어서 점점 $\mathcal{T'}$ 의 평균적인 근사 표현이 만들어질 것이다.
이러한 방법을 사용해서 테스트를 진행하였을 때
생각보다 높은 55%의 성능이 나왔는데 이는 $h$ 가 transform의 근사와 관련이 있다는 가설이 맞다는 것을 보여준다.

6. Comparison

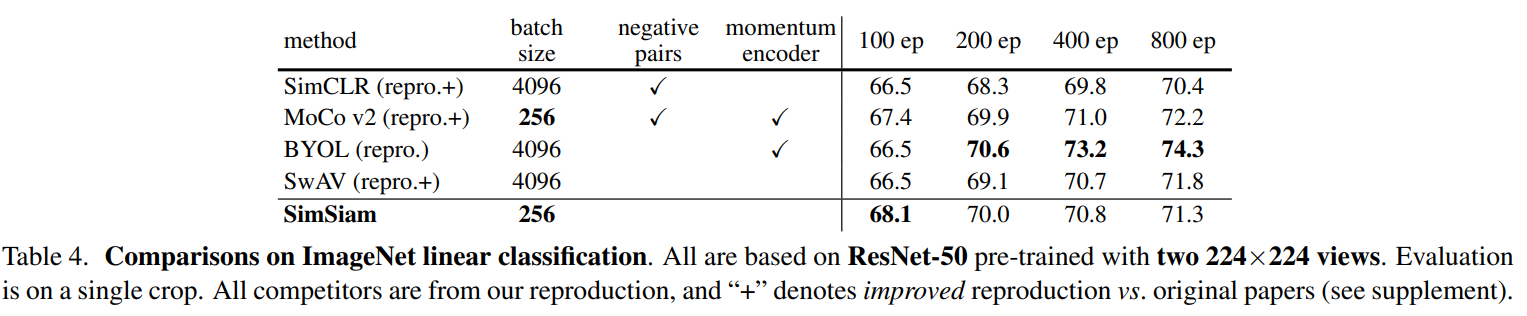
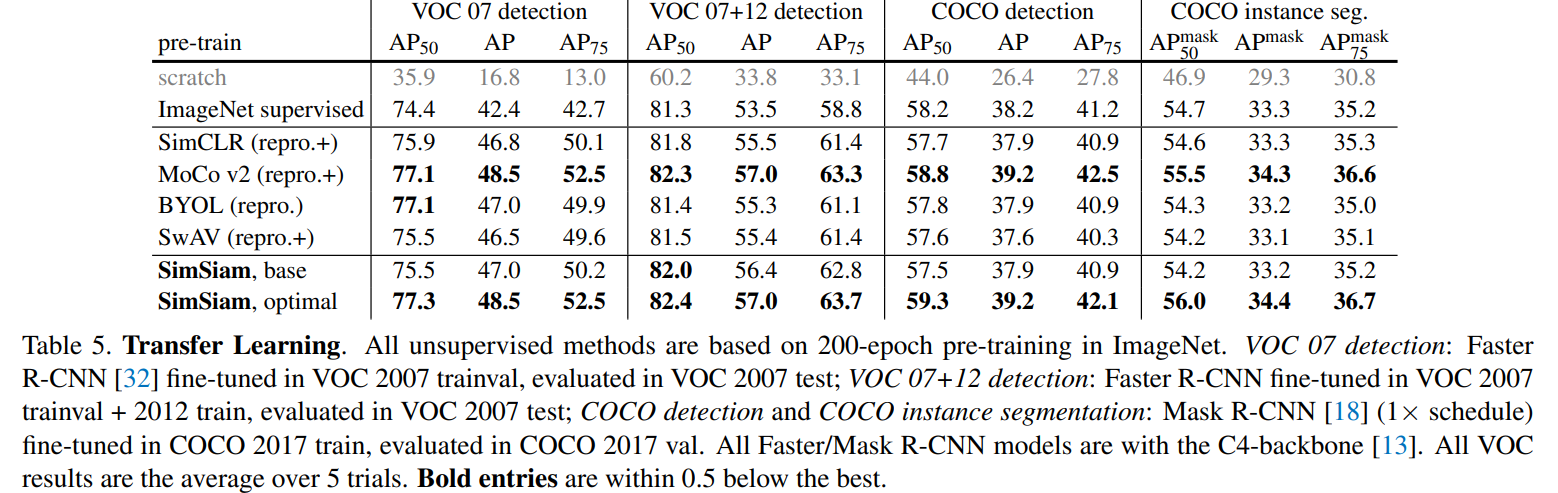간단한 구조로 높은 성능을 보여줌
이때 100epoch 이하에서는 높은 성능을 보여줬지만 학습이 길어질수록 얻는 이점이 감소하였다.

구현

class SimSiam(Framework):
    def __init__(self, device, args, dim=128):
        model = load_model(args.model, class_num=dim)
        super().__init__(model, criterion=nn.CrossEntropyLoss(), device=device)
        dim_mlp = self.encoder.out.weight.shape[1]
        hidden_dim = 2048
        self.encoder.out = nn.Sequential(
            nn.Linear(dim_mlp, hidden_dim),
            nn.BatchNorm1d(hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.BatchNorm1d(hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.BatchNorm1d(hidden_dim),
            nn.ReLU(),
        )
        self.predictor = nn.Sequential(
            nn.Linear(hidden_dim, hidden_dim // 4),
            nn.BatchNorm1d(hidden_dim // 4),
            nn.ReLU(),
            nn.Linear(hidden_dim // 4, hidden_dim),
        )
        self.encoder = self.encoder.to(device)
        self.predictor = self.predictor.to(device)

    def forward(self, batch):
        x1, x2 = batch[0][0].to(self.device), batch[0][1].to(self.device)
        # (batch, 3, 32, 32)
        z1 = self.encoder(x1)
        z2 = self.encoder(x2)
        p1 = self.predictor(z1)
        p2 = self.predictor(z2)

        loss = (self.loss_(p1, z2.detach()) / 2) + (self.loss_(p2, z1.detach()) / 2)
        return loss.mean()

    def loss_(self, x1, x2):
        x1 = F.normalize(x1, dim=-1, p=2)
        x2 = F.normalize(x2, dim=-1, p=2)
        return -(x1 * x2).sum(dim=-1)

pyross

AGI

이전 포스트

[논문 리뷰 및 구현] Bootstrap Your Own Latent A New Approach to Self-Supervised Learning

다음 포스트