[논문 리뷰] What Makes for Good Views for Contrastive Learning?

논문 링크

contrastive learning의 view를 중점으로 다룬 논문
이전에 Contrastive Multiview Coding 논문에서 실험 부분에서 mutual information과 성능의 관계에 대해서 나온 적이 있다.

Abstract

contrastive learning이 요즘 떠오르고 있지만 보통 view의 구성에 많은 영향을 받는다.
이 논문은 그 view의 영향에 대해서 다루었다.

mutual information을 줄이는 동시에 task-relevant information은 보존해야 한다.

1. Informaton

우선 퓨네스의 저주에 대해서 설명을 하고 시작한다.
퓨네스의 저주란 "314번째로 본 개와 315번째 본 개는 똑같이 개로 불러야 한다."라는 것인데 정리하자면
퓨네스는 너무 기억력이 좋은 나머지 특정 부분이 조금만 달라져도 완전히 다른 객체로 인식한다.

반면에 우리는 객체를 대표 representation으로 표현할 때 뉘앙스를 버린다.(봤던 장소, 봤던 시간,보는 각도, 심하게는 강아지의 색 등등)
즉 view-invariant representation을 구축하는 것이다.
이는 여러개의 view를 가지고 이를 공통적으로 표현하는 방법을 학습하는 multi view learning에 중점을 두고있다.

그러나 multi view에서 어느 부분을 invariant하게 만들어야 하는지가 문제가 된다.

만약 우리가 시간을 분류하는 representation을 만들어야 한다면 시간이 고정이된 view를 사용하면 안된다.(시간이 고정이된 표현을 학습할 수밖에 없기 때문에)
만약 그렇게 된다면 퓨네스처럼 시간이 조금만 달라져도 다른 이미지로 인식하게 될 수 있다.

시간을 표현할 수 없으니 다른 시간에 본 같은 개를 다른 개로 인식
즉 view에 따라서 표현이 매우 달라진다.

• 결국 중요하지 않은 정보는 달라지지만 downstream task에 중요한 정보는 버리지 않는 robust한 view를 사용하는 것이 중요하다.

이를 위해 논문의 저자는 다양한 방법을 사용하였다.
1. downstream task에 따른 optimal view 조합을 확인(task를 알면 최적의 view를 구성할 수 있음)
2. mutual information이 너무 낮거나 너무 높게 만들지 않아서 downstream performance에 적합한 view의 조합을 확인

또한 "infoMin" principle을 제시하는데 이는 좋은 view들의 조합은 downstream task가 잘 작동하기 위해서 필요한 information을 최소로 공유하는 것이라는 이야기이다.

또한 이를 위해 효과적인 view를 학습하는 semi-supervised learning 방법을 제시하였다.

3 What Are the Optimal Views for Contrastive Learning?

3.1 Multiview Contrastive Learning

바로 이전에 리뷰했던 Contrastive Multiview Coding의 내용과 겹치는 부분이 많다.
이 논문을 참고하면 좋을 것 같다.

새로운 정의가 나오는데

definition 1. (sufficient encoder) view $\mathbf{v_1}$의 encoder $f_1$은 다음을 만족해야만 contrastive learning에 충분하다.
$I(\mathbf{v_1};\mathbf{v_2})=I(f_1(\mathbf{v_1});\mathbf{v_2})$
즉 encoder가 정보의 손실을 만들면 안된다. 이는 $\mathbf{v_2}$도 마찬가지이다.
이를 통해 contrastive learning에 필요한 모든 정보가 보존이 된다.

definition 2. (Minimal Sufficient Encoder)
encoder $f_1$은 다음의 경우 minimal이다.
$I(f_1(\mathbf{v_1});\mathbf{v_1}\leq I(f(\mathbf{v_1});\mathbf{v_1}) \forall f$ 이때 모든 $f$가 sufficient이면 성립한다.

즉 sufficient encoder 중에서 minimal은 contrastive에 필요한 정보만 남기고 불필요한 정보는 다 지울 수 있다.
이는 view를 downstream task위주로 구성을 할 때 이득을 볼 수 있다.

definition 3. Optimal Representation of a Task
input data $\mathbf{x}$로 label $\mathbf{y}$를 예측하는 task $\tau$가 있을 때 $\mathbf{x}$를 encoding해서 만든 $\mathbf{z}^*$는 $\mathbf{y}$에 대해서 minimal sufficient statistic을 가진다.
즉 $\mathbf{y}$를 예측하기 위해서 필요한 최소한의 정보를 다 담고있다는 뜻이다.

3.2 Three Regimes of Information Captured

2개의 view로부터 $\mathbf{z_1}$,$\mathbf{z_2}$가 만들어지는데 공유되는 정보의 양과 type이 view에 매우 큰 영향을 받는다.
이는 downstream task의 성능에 영향을 준다.

여기에서 view를 조절해서 공유되는 정보의 양과 downstream task의 정확도를 비교하였다.
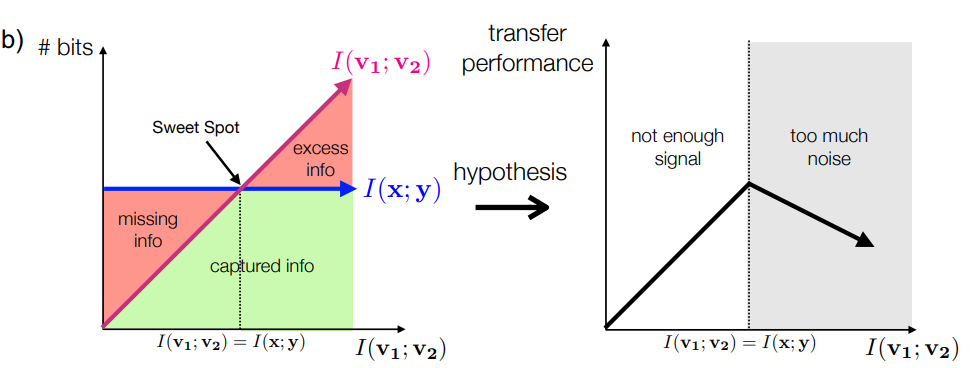왼쪽 그림을 보면 $I(\mathbf{v_1};\mathbf{y})$, $I(\mathbf{v_2};\mathbf{y})$를 유지하면서 $I(\mathbf{v_1};\mathbf{v_2})$를 줄일 수 있는 view를 구축하였는데
그 구간이 3가지가 나온다.
1. $I(\mathbf{v_1};\mathbf{v_2})$가 너무 많으면 noise가 많이 껴서 중요한 정보가 버려지게되고
2. 만약 너무 적으면 학습할 정보가 적어서 정확도가 낮아진다.
3. $I(\mathbf{v_1};\mathbf{y})= I(\mathbf{v_2};\mathbf{y})=I(\mathbf{v_1};\mathbf{v_2})=I(\mathbf{x};\mathbf{y})$인 구간이 가장 성능이 잘나왔다.

최적의 view는 다음의 식을 만족한다.
$(\mathbf{v_1^*},\mathbf{v_2^*})=\arg\min_{\mathbf{v_1}\mathbf{v_2}}I(\mathbf{v_1};\mathbf{v_2})$인데 이때 $I(\mathbf{v_1};\mathbf{y})= I(\mathbf{v_2};\mathbf{y})=I(\mathbf{x};\mathbf{y})$를 만족해야 한다.
이를 위해 domain knowledge를 통해 적절한 view를 정해야 한다.

3.3 View Selection Influences Mutual Information and Accuracy

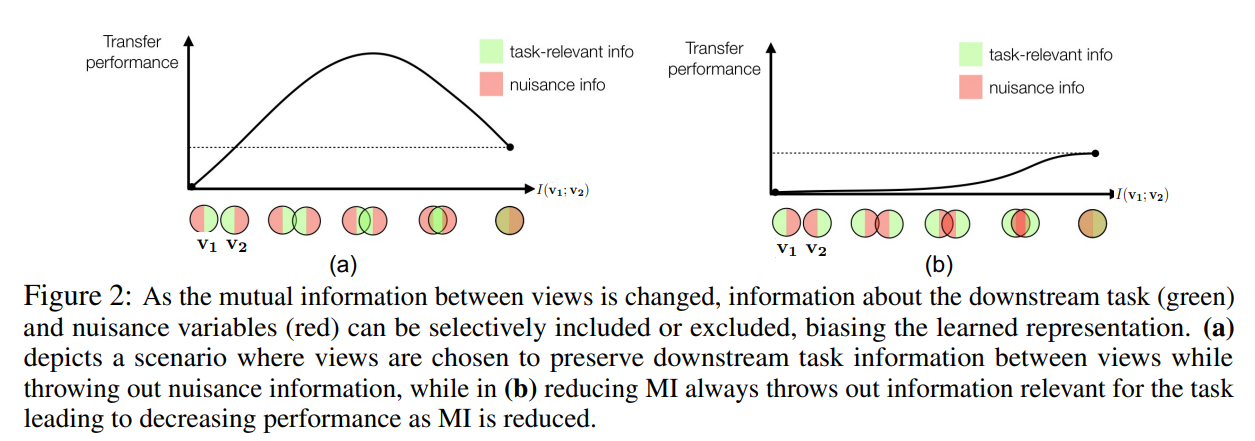이전에 언급했던 내용대로 task-relevant info가 많고 noise를 만드는 info가 적을수록 좋은 성능을 보인다.
위 실험을 위해 이전 논문 처럼 patch의 거리를 바꿔가면서 info를 조절하였다.(거리가 멀면 정보 적고 거리가 가까우면 정보 많다.)
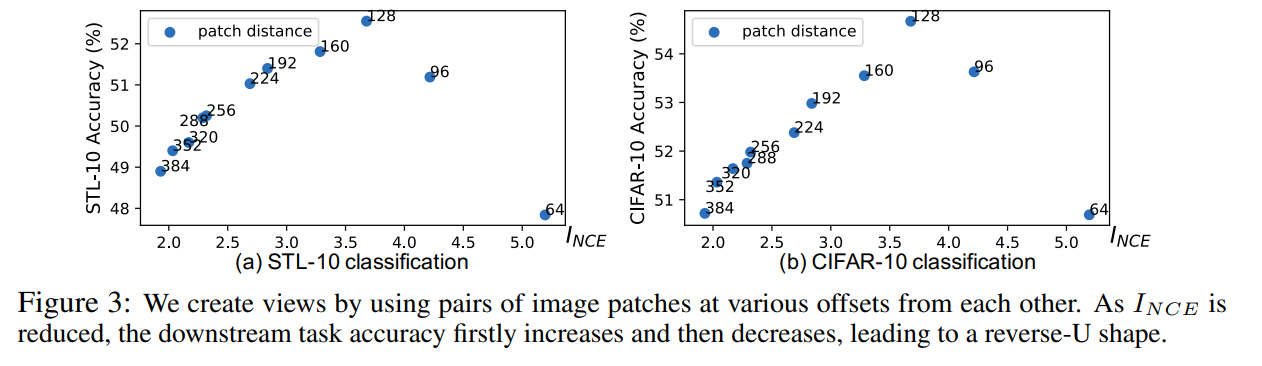정보는 $I_{NCE}$라고 한다. 이전의 infoNCE 수식의 평균으로 생각된다. encoder를 얼리고 linear classifier를 학습하는 식으로 진행하였다.

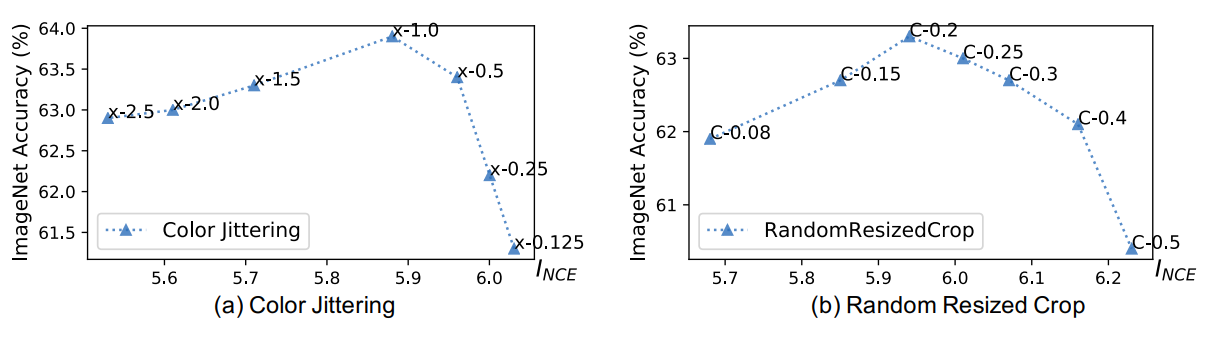
3.4 Data Augmentation to Reduce Mutual Information between Views

다른 것들과 비교해서 augmentation만으로 매우 큰 성능향상을 이끌어냈다.
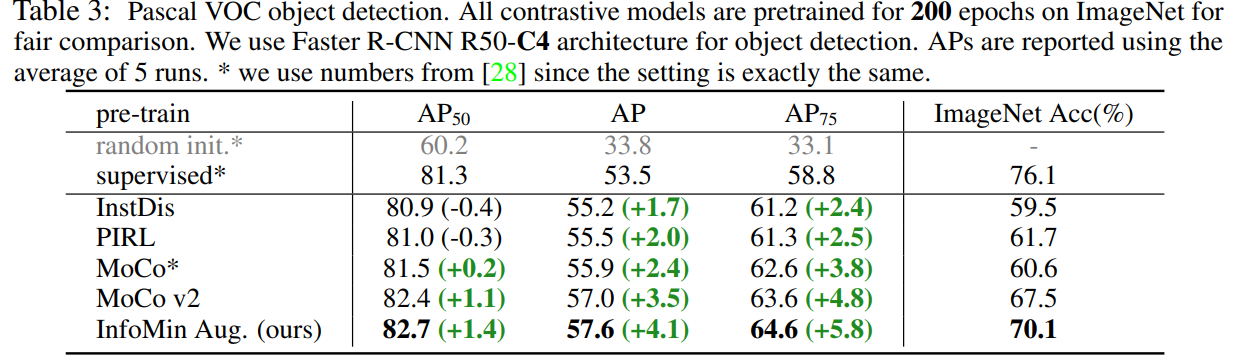
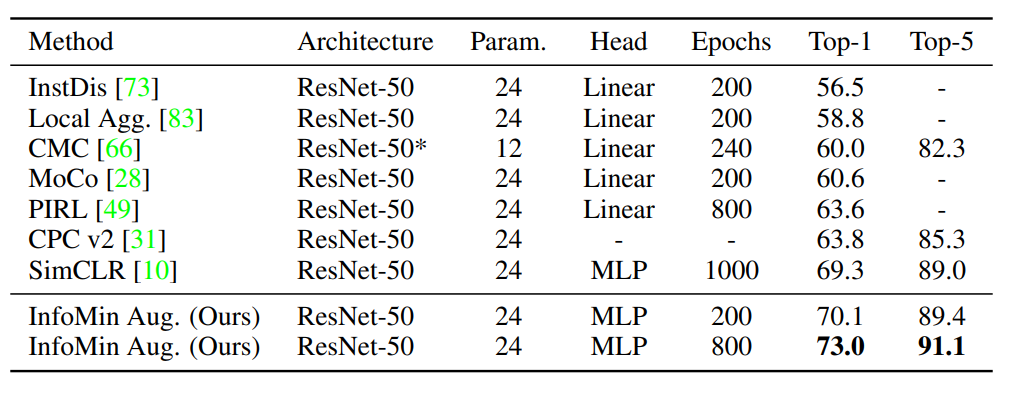object detection 분야에는 supervised보다 좋은 성능을 보임

4. Learning views for contrastive learning

위 실험에서 사용했던 직접 손으로 만든 augmentation은 효과적일 때가 많지만 새로운 domain에서는 비효율적일 때가 있을 수 있다.
또한 augmentation은 downstream task에 중요하다.
여기에서는 view를 data에서 학습하는 방법을 제시한다.

4.1 Optimal Views Depend on the Downstream Task

실험을 진행
dataset : movind MNIST(검은 화면에 숫자 움직이는 것) + STL-10을 배경
즉 데이터에 factor 3가지 (숫자, 숫자의 위치, 배경 class)
view v1은 sequence of past frames로 고정 view v2는 $X_t$를 참조해서 만든다.
1. digit 위치 고정
2. digit 고정
3. background image 고정
아래와 같이 구성
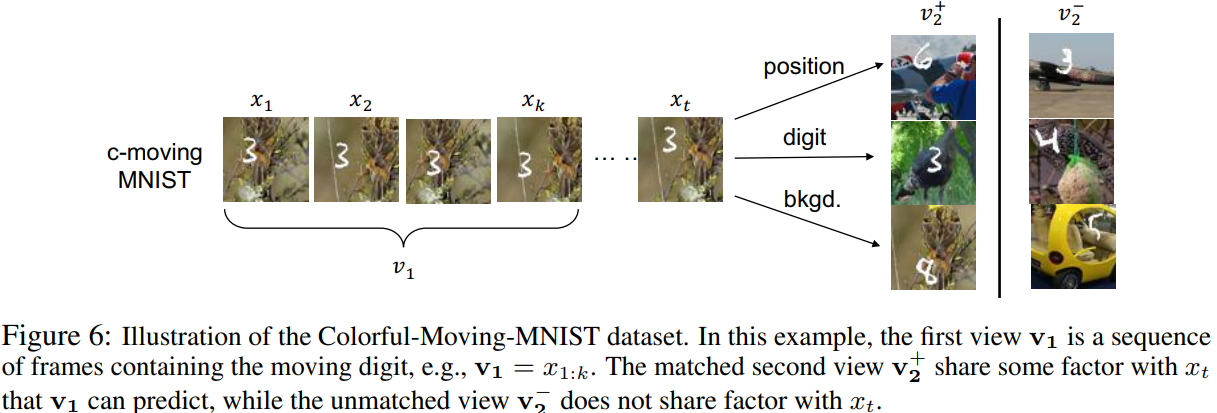이후 view가 얼마나 영향을 주는지 확인
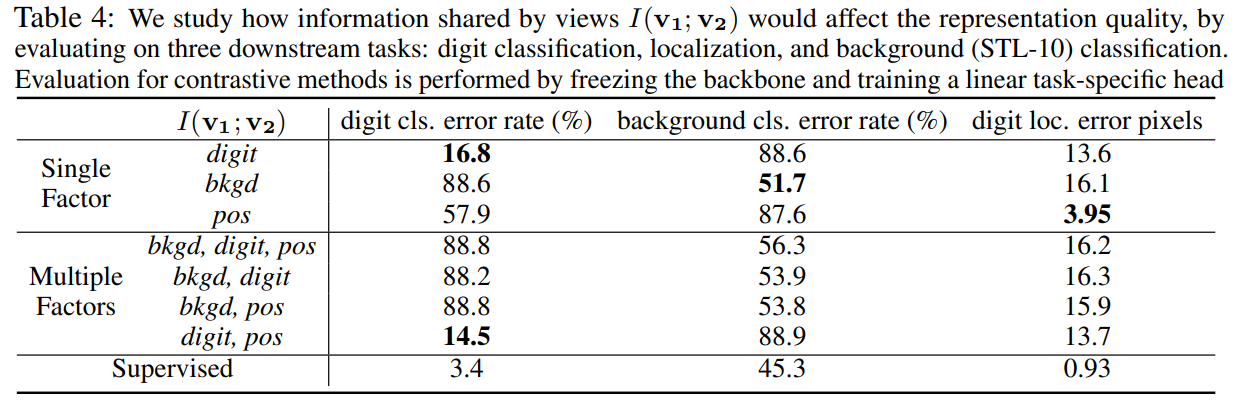multiple factor로 공유되는 정보가 많아지면 역시 성능이 매우 떨어진다. 특이한건 bkgd의 정보가 공유가 되면 다른 정보를 모두 압도해서 어떤 것을 넣든지 성능이 떨어지게 된다.

4.2 Synthesizing Views with Invertible Generators

새로운 뷰를 만드는 방법을 연구
구체적으로 flow model을 만들어서 기존의 색 space를 새로운 color space로 바꾼다. 이후 채널을 통해 분리해서 view를 만든다.
이때 flow model은 픽셀 기반으로 적용이 되며 양방향 전환이 가능하다.

flow model $g$는 1x1 conv와 ReLU로 구성이 됨
이때 부피 보존 흐름(VP)과 비부피 보존 흐름(NVP)으로 구성 전부 다 실험해봄
이미지 $X$의 채널 분할은 $\{X_1,X_{2:3}\}$으로 표현이 되고
transform은 $\hat X$로 표현이 됨

4.2.1 Unsupervised View Learning: Minimize I(v1; v2)

$\min_{g} \max_{f_1, f_2} I_{\text{NCE}}^{f_1, f_2} \left( g(X)_1 ; g(X)_{2:3} \right)$이 수식을 통해 학습을 진행한다.
g는 둘 사이의 공유되는 정보를 최소화 하고 f1,f2는 정보를 최대한 모은다.
결과는 다음과 같다.
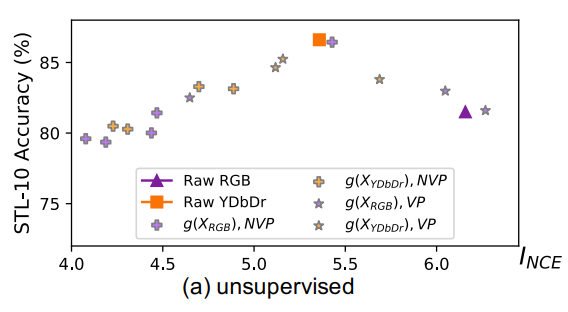이때 rwa YDbDr은 시작부터 sweet spot에 가장 근접했다. 이는 이러한 방법이 색을 구별하면서 객체를 인지하기 좋은 방법이라는 사람의 인식과 일치하기 때문이라는 것 같다.

또한 g를 사용하게 되면서 공유되는 정보가 줄어들게 되었는데 이때 학습이 불안정하다는 것을 발견하였다.(위 사진을 보면 여기저기 흩어져 있음)
왜냐하면 g는 downstream task(y)에 대한 정보가 없기에
$I(\mathbf{v_1};\mathbf{y})= I(\mathbf{v_2};\mathbf{y})=I(\mathbf{x};\mathbf{y})$가 무너지기 때문이라고 생각하였다.
즉 $I(\mathbf{v_1};\mathbf{v_2})$만 가지고 진행하기 때문에 기준이 없음.

4.2.2 Semi-supervised View Learning: Find Views that Share the Label Information

위와 같은 문제를 극복하기 위해 semi-supervised learning 방법을 고안하였다.

down stream을 위한 소수의 label이 사용이 가능하다고 할 때
g가 $I(g(X)_1,y)$와 $I(g(X)_{2:3},y)$의 정보를 얻을 수 있다.
$\min_{g, c_1, c_2} \max_{f_1, f_2} {I_{\text{NCE}}^{f_1, f_2} \left( g(X)_1 ; g(X)_{2:3} \right)} + {\mathcal{L}_{\text{ce}} \left( c_1(g(X)_1), y \right) + \mathcal{L}_{\text{ce}} \left( c_2(g(X)_{2:3}), y \right)}$
이렇게 구성이 되는데
왼쪽은 unsupervised 부분이고 오른쪽(y가 있는)부분은 supervised 부분이다.

간단하게 unsupservised 부분에다가 +로 supervised 부분을 추가한 것이다.
c는 classfier이고 $L_{ce}$는 cross entropy일 것이다.
unsupervised는 이전과 같이 $I(\mathbf{v_1};\mathbf{v_2})$를 감소시키고
supervised 부분은 $I(\mathbf{v_1};\mathbf{y}), I(\mathbf{v_2};\mathbf{y})$를 유지시킨다.
즉 downstream task에 필요한 정보는 유지한다.

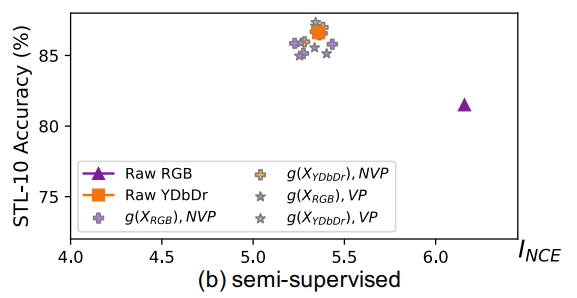이전과 다르게 downstream task의 정보를 알 수 있기 때문에 안정적으로 honey spot으로 모여있다.

view generator 실험 결과 semi가 가장 효과가 좋다.

conclusion

좋은 view는 downstream task에 대한 정보를 최소로 유지해야 한다.