Naive Bayes Classifier

new instance가 들어올때의 상황을 생각해보자. 우리가 $v_{MAP}$ 을 구하려 할때, instance $<a_1, a_2, \cdots,a_n>$을 생각하면

이고, 베이즈 정리에 의해 다음처럼 나타낼 수 있다.

여기서 문제가 발생간다. $P(v_j)$는 모르면 uniform하게 둘수있지만, 앞의 joint prob은 알수없다.
따라서 naive하게 생각을 하는것이다.

Naive Bayes Classifier

Naive하게 아까의 joint prob 계산을 모두 conditionally independent 하다고 놓고 계산을 하는것이다.

Definition. Naive Bayes Classifier

Under the naive Bayes classifier, the target value output $v_{NB}$ is determined by
$\qquad \qquad v_{NB} = \underset{v_j\in V}{\text{argmax }}P(v_j)\prod_i P(a_i|v_j)$

이렇게 independent일 경우 모든 확률의 곱으로 나타낼 수 있으므로 계산이 가능해진다.

그렇다면 예제를 보자

---

Example. Play Tennis?

$\\$
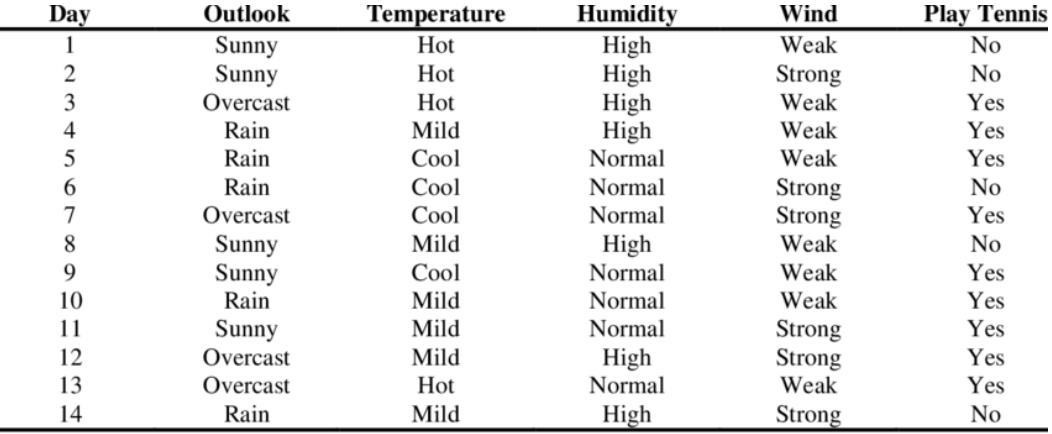
Consider the following novel instance
<outlook=sunny, temperature=cool, humidity=high, wind=strong> 이때, 과연 테니스를 플레이할것인가?

Target value $v_{NB}$는 다음처럼 구할 수 있다.

그리고 $P(v_j)$ 는 이미 데이터를 통해 알고있다.

그렇다면 이제 새로운 instance에 대한 확률을 계산하면 된다.

(나머지 계산은 생략)

이런식으로 모두 확률을 찾은뒤에, 단순히 곱해주기만 하면된다.

그렇다면 우리는 naive Bayes Classification의 결과가 "PlayTennis=no" 라고 분류할 수 있다.

---

Laplace Smoothing (Laplacian Correction)

나이브 베이시안 분류기를 사용할때 라플라스 스무딩이라는걸 해줘야한다.

왜냐하면 위에서 $v_{NB}$의 식이 다음과 같았다.

그런데 만약 $P(a_i|v_j) = 0$ 이라면? (or 0에 가까운 값) $\to$ 어떤 확률이 존재하던지 0이 나오게 된다.

따라서 이를 방지하고자 다음처럼 smoothing을 진행한다.

$n : \text{total num of training example}$
$n_c : \text{num of }a_i | v_j\\ e.g. \;\; P(\text{Wind=strong}|\text{PlayTennis=no}) : n=5, n_c = 3$
$m : \text{equivalent sample size }(m = 0 \text{ means no laplace smoothing})$
$p : \text{probabilistic weight to }m; \text{normally set to }\frac{1}{k}\\ \quad\;\text{where }k \text{ is the num of attribute values, e.g. Wind = 2}$