ML
1.Bayesian Learning

베이시안 러닝은 Training data를 받아 나의 belief를 업데이트 하는 방식이다.기존에 알고 있던 방법중 하나인 Maximum likelyhood는 $\\mu$와 $\\sigma$를 알지, 베이시안 러닝은 이를 모른다는것이 둘의 차이점이다.data D가 주어
2.Bayes Theorem and Concept Learning

이제 베이즈 정리와 concept learning간에 어떤 관계가 있을지 생각해보자.instance $<x_1, \\cdots,x_m>$이 있고, training data D를 $D = \\;<d_1, \\cdots, d_m>$ 이라 해보자.For each
3.Bayes Optimal Classifier

우리가 이제 새로운 instance가 들어왔을때, 어떻게 분류를 하는것이 최적일지 생각해 보아야 한다.이전처럼 단순히 $h\_{MAP}$ 으로 아래의 예제를 생각해보자.Given a new instance $x$$h1(x) = \\oplus, \\quad h_2(x)
4.Naive Bayes Classifier
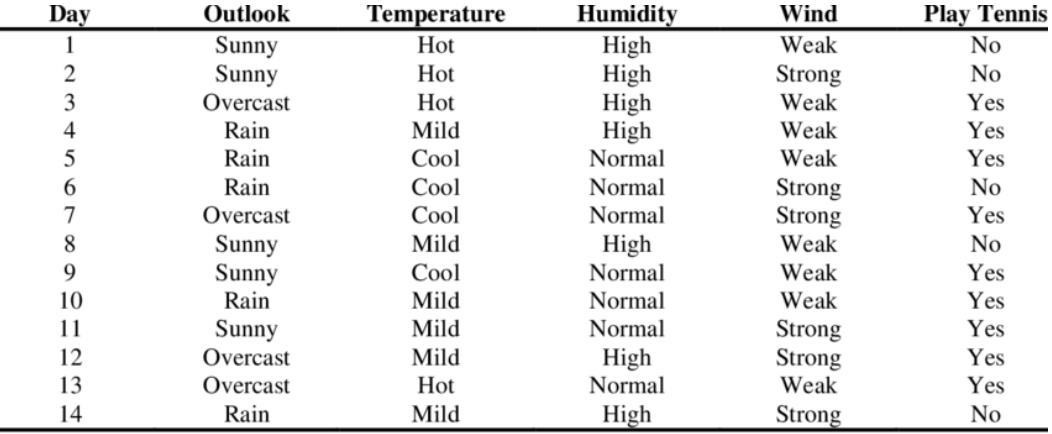
new instance가 들어올때의 상황을 생각해보자. 우리가 $v_{MAP}$ 을 구하려 할때, instance $$을 생각하면 $$v{MAP} = \underset{vj\in V}{\text{argmax}}\;P(vj|a1,a2,\cdots,an) $$ 이고,
5.Bayesian (Recursive) Estimation
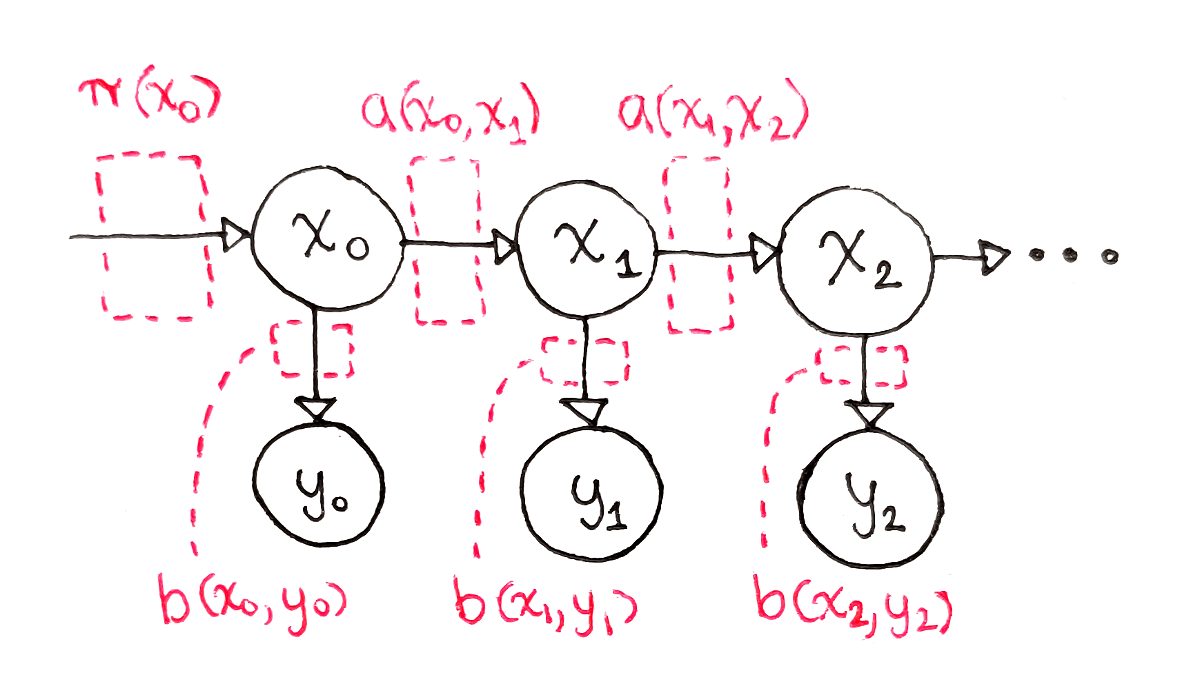
Bayesian Estimation을 설명하기 위한 몇가지 이론들을 먼저 보자.문이 하나 존재하고, 문의 상태를 $X$, 센서의 관측을 $Z$라 하면 $$X = \\left { \\text{open , closed}\\right } \\qquad Z = \\left
6.Is Learning Feasible?
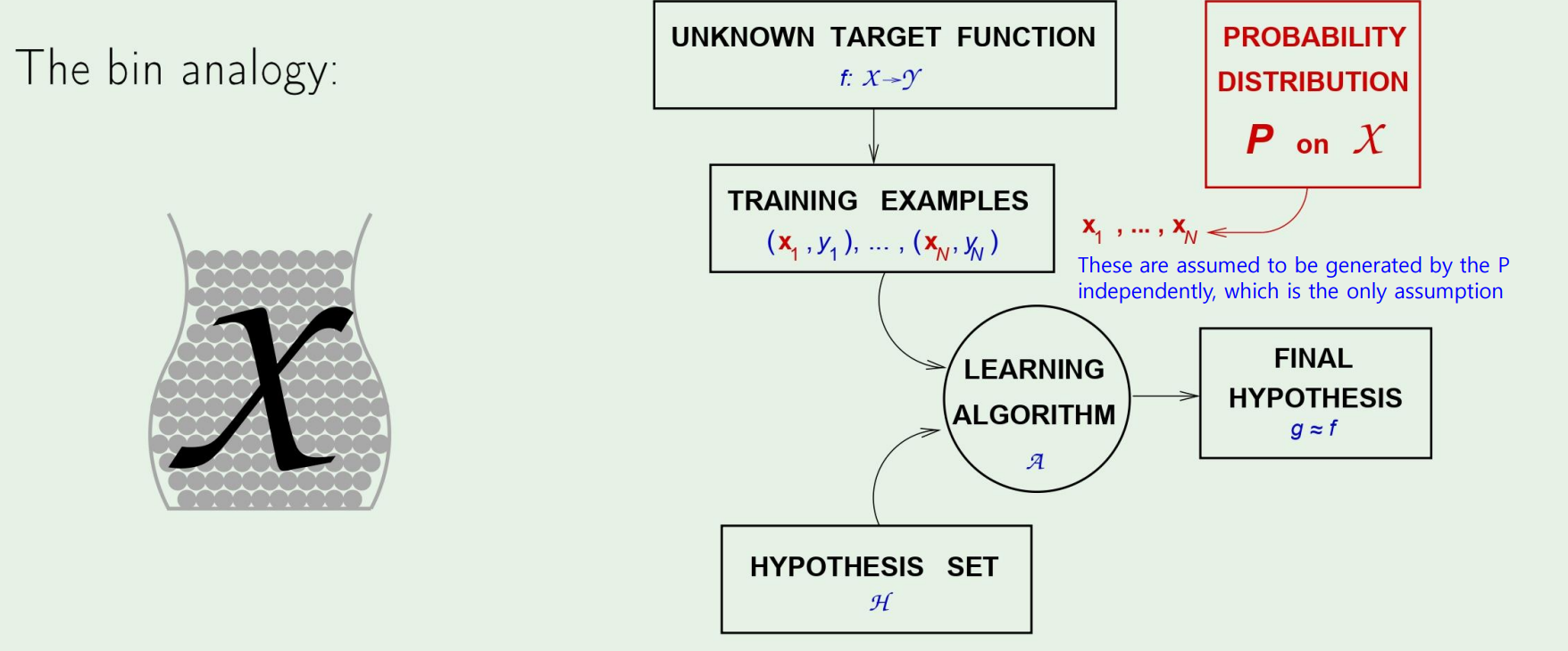
이번 주제는 과연 학습한다는것이 실현 가능한지 이론적으로 알아보겠다. $\to$ PAC-Learnable 한가? (Probably, Approximately, Correct) 먼저 한가지 예제를 살펴보자. 이러한 간단한 분류 알고리즘이 있다고 하자. 그렇다면 저
7.The Linear Model

저번 포스팅을 리뷰하면, Learner을 디자인해서 문제를 해결하는것이 왜 Feasible한지 살펴보았다.그렇다면 이번 포스팅에서는 이를 Linear model에 대해 살펴보겠다.우리가 잘 알고있는 MNIST data를 보자이 데이터로 classification을 진행
8.Error and Noise
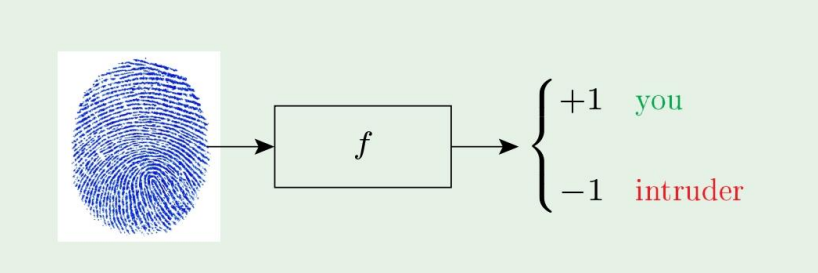
저번 포스팅에서는 Linear model에 대해 다루었다. 마지막에 Nonlinear transformation에 대해 보았는데, 이번 챕터에서도 계속 보겠다. Nonlinear transformation (continued) 여기서처럼 Inverse mapping
9.Train versus Testing
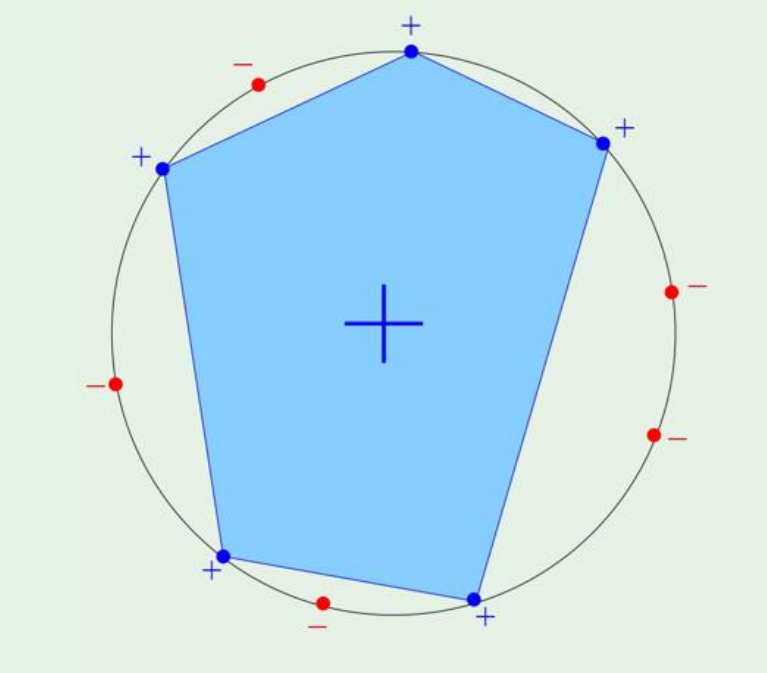
우리의 PAC learnable한 model이 어떻게 error를 bound했는지 살펴보았다. 지금껏 우리의 호패딩 형님이 알려주었듯이, $$\mathbb{P}\left [ |E{\text{in}} - E{\text{out}} > \epsilon\right ] \le
10.Theory of Generalization
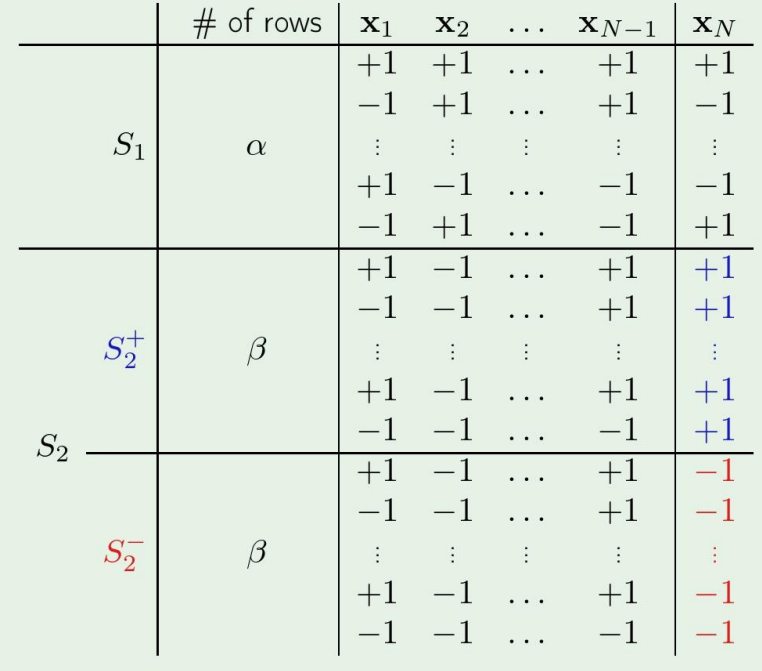
저번에는 왜 우리가 Dichotomiy라는 개념을 도입했는지, 왜 Growth function을 사용하는지를 배웠다.잠깐 복습을 해보자.Growth function이란, N개의 sample이 주어졌을때, 거기서부터 내가 정의할수있는 최대 dichotomiy의 갯수이다.
11.The VC Dimension
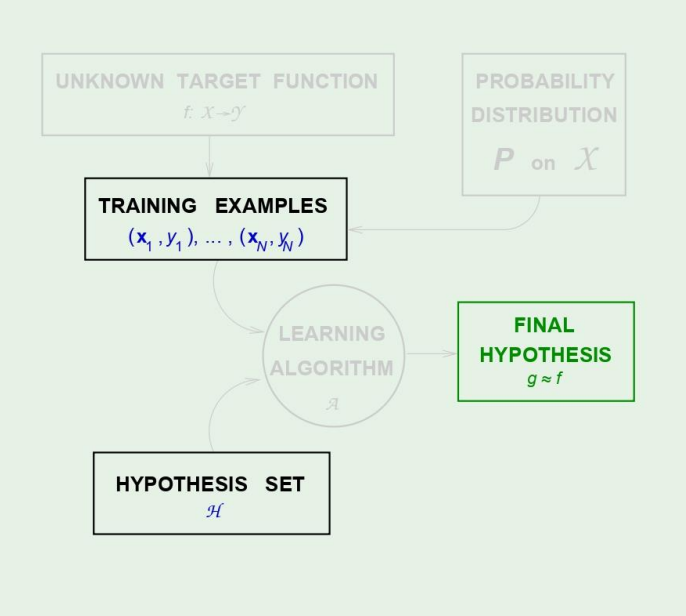
저번에는 growth function을 polynomial하게 만들수있는지와, 아주 얕게 VC Inequality에 대해 보았다. 이번에는 가장 중요한 VC dimension에 대해 보겠다. Definition of VC dimension The VC dimens
12.Bias-Variance Tradeoff
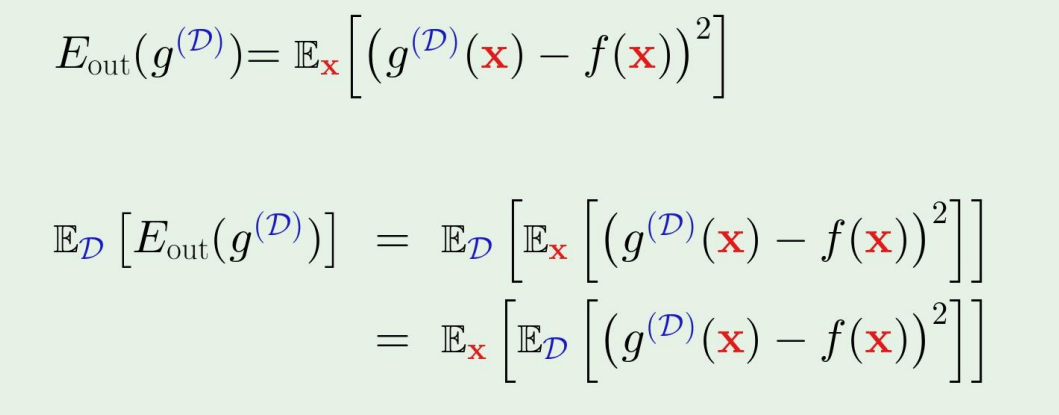
우리의 목적은 out of sample error, 즉 $E\_{\\text{out}}$이 낮은 learner을 얻고자 하는 것이다.이 learner을 얻기 위해서는 우리가 2가지 방법을 생각할 수 있다.More complex $\\mathcal{H}$ $\\Right
13.Support Vector Machine-1

SVM은 지금까지 보았던 교재를 보기전에, 학교 교수님의 자료를 먼저 보면서 이해해 보겠다. Support Vector Machine 기존에 우리가 보았던 아달린(선형분류)이나, 로지스틱(비선형분류)의 확장이라 생각하면 된다. 그럼 어떤것이 확정되었는가? 바로 M
14.Support Vector Machine-2
지난글에 간단히 SVM이 무엇인지, 우리가 문제를 어떻게 formulation해야 하는지를 살펴보았다. 기존의 constrained optimization문제를 unconstrained optimization으로 풀수있게 해주는 놀라운 발견을 예시로 잠시 살펴보겠다.
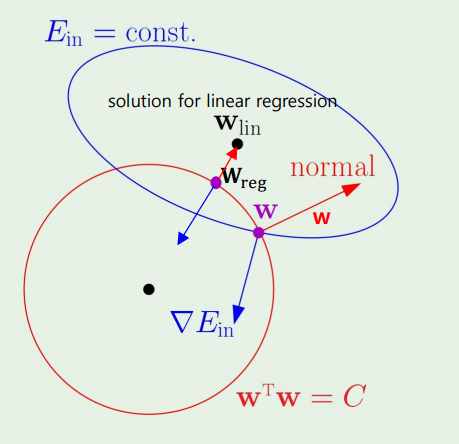
15.Regularization
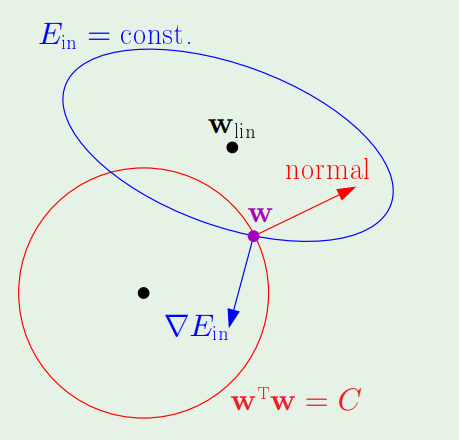
이번 장에서는 Regularization, 그중에서도 curve fitting problem만 간단하게 다뤄보겠다. 이러한 점들이 존재할때, 과연 몇차원으로 fitting을 해야할지 결정하는 것이다. (polynomial regression) 결론부터 말하면, 내
16.Support Vector Machine-3
이제 최종적으로 다시 원래 교재로 돌아와, SVM을 마무리 하겠다. Better linear separation 기존에는 그냥 단순히 저 보라색 선만 긋는, 즉 margin없이 분류하는것에 대해서만 배웠다. 그렇다면 margin이 왜필요할까? 결론부터 말하자면,
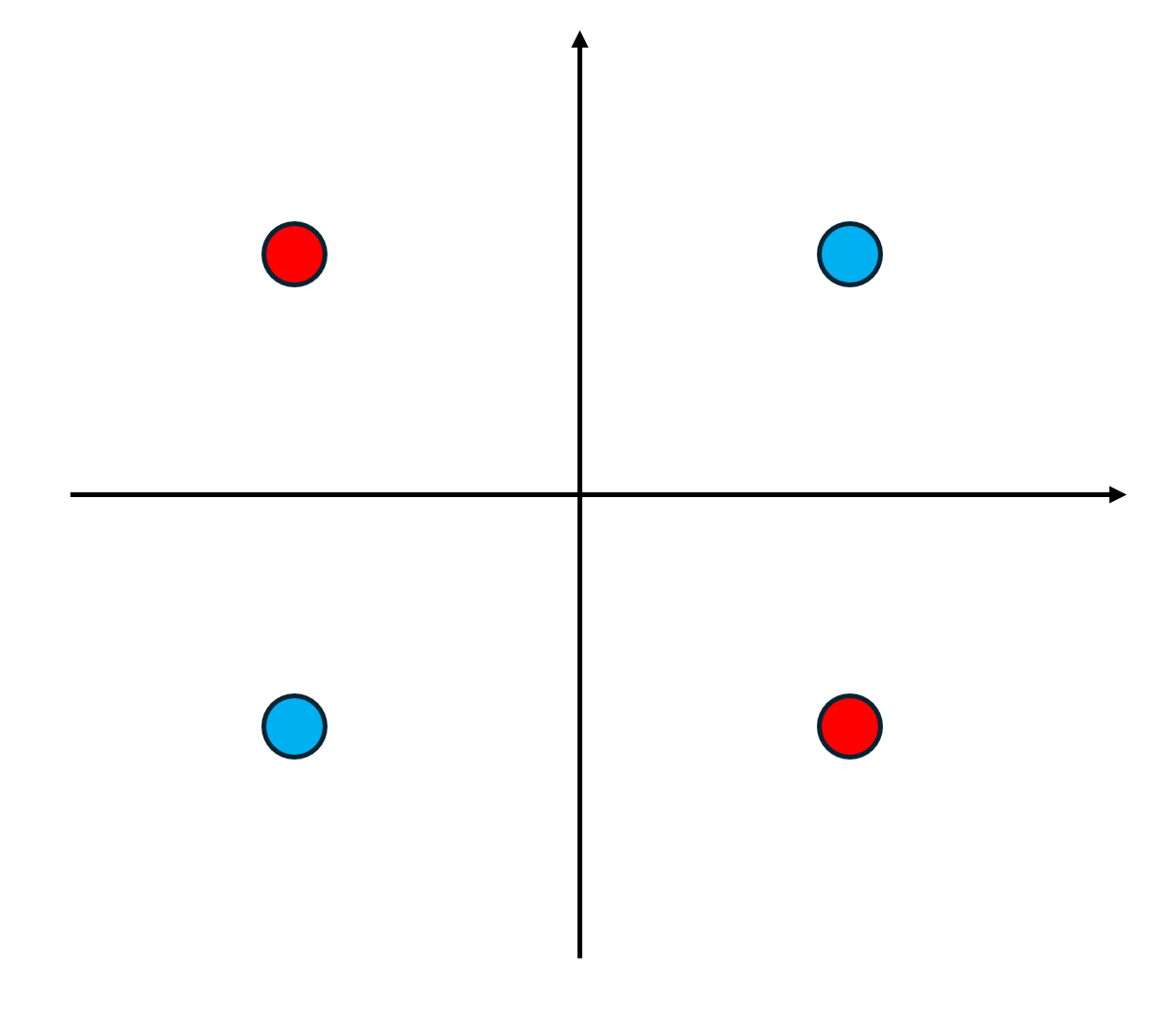
17.Kernel Methods
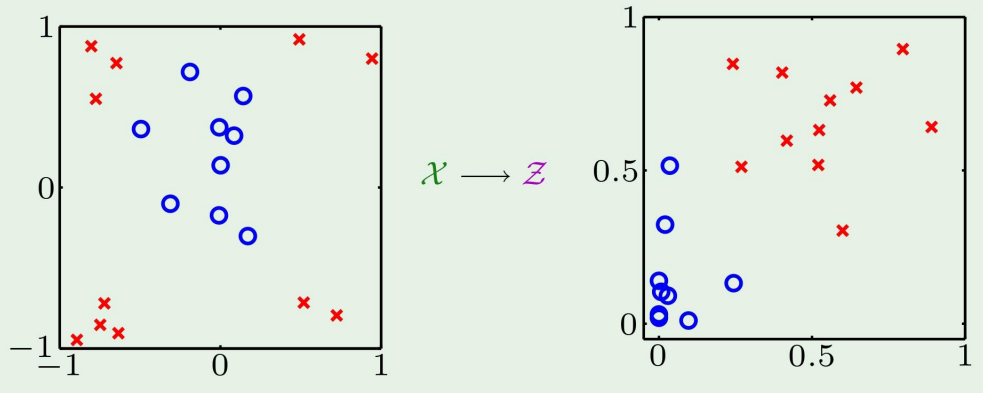
저번에 우리가 $\\mathcal{X}$ space에서 $\\mathcal{Z}$ space로 공간을 이동시켰고, 이렇게 하는 방법이 kernel method라고 하였다.이 방법을 자세히 다뤄보자.SVM에서의 $\\mathcal{L}(\\alpha)$ 식을 다시 떠올려