BV algorithm

BV 알고리즘은 숨은 string s를 찾는 알고리즘이다.
다음과 같이 $f : \{0,1\}^n \mapsto \{0,1\}$ 가 있다고 하자
이 함수는 숨은 비밀 string s 와 내적값을 뱉어준다.

s는 x와 똑같은 n 비트 스트링이고 고정된 비밀 값이다.
x는 입력으로 우리가 아무 값이나 넣을 수 있다.

원래대로라면 f를 이용해서 s를 어떻게 구할 수 있을까??

한번 생각해보면 간단히 one-hot 벡터를 이용하면 된단걸 알 수 있다.
그냥 방정식으로 생각해봐도 s1부터 sn까지 n개의 미지수가 있으니 그냥 n개의 방정식만 있으면 어떻게든 구할 수 있다.

제일 간단한 방법은 다음과 같이 원핫 벡터를 이용해 원소를 하나하나 뽑아내는 것이다.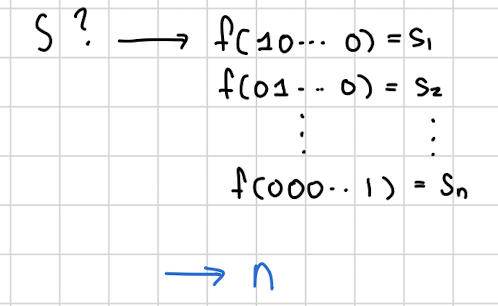

n번 f값을 구해야한다.
하지만 또다시 퀀텀은 이걸 단 1번에 할 수 있다...!

S를 구하는 방법은 저번에 배운 DJ 알고리즘과 그냥 똑같다.
그래서 왜 이게 되는지 이해하는게 더 중요하다고 볼 수 있다.

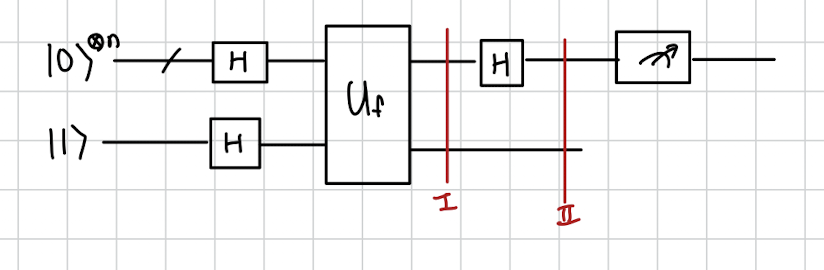
보는 대로 저번 배운 DJ와 똑같다는걸 알 수 있다.

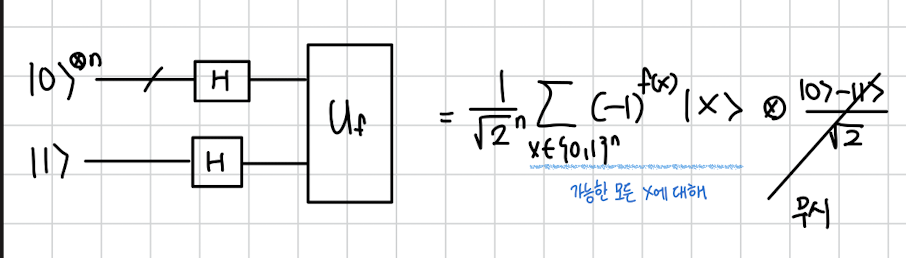
마지막 $|-\rangle$ 상태는 $f(x)$를 첫번째 큐빗의 부호에 오게 하는 것 말고 그 후로 역할이 없으니 무시해도된다.

여기까지 가능한 모든 n 비트 x에 대해 각 f(x)값이 x의 부호를 결정하는 superposition상태가 완성되었다.

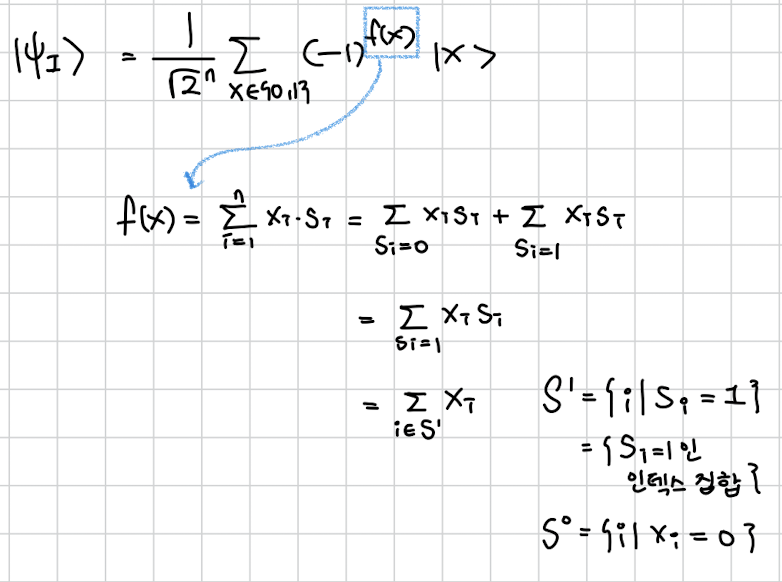
여기서 우리는 f(x) 를 내적이라는 정의에 맞게 다시 정의해봐야한다.

f(x)값은 s가 0과1의 string이니까 결국 , s가 1인 자리에 x도 1이 몇개가 있냐? 가 된다.

그걸 수학적으로 하면 저렇게 S1집합을 s가 1이자리를 나타내는 인덱스 집합으로 나타낼 수 있다.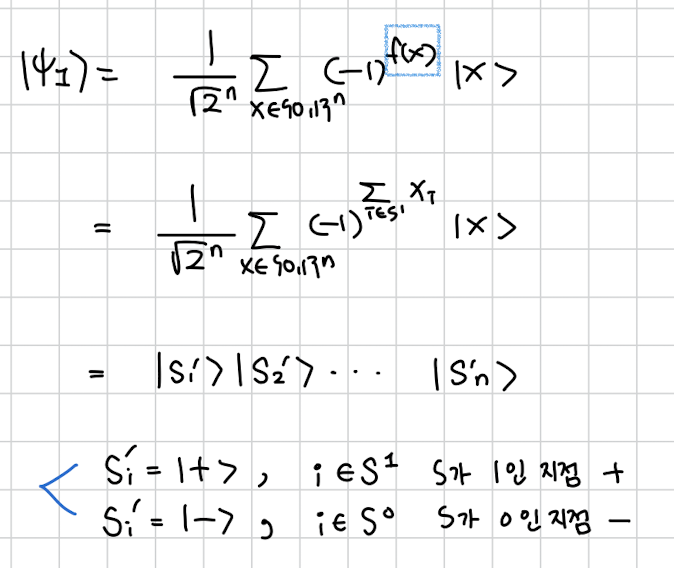

정의한 f(x)를 식에 넣고 결론을 보면 다음과 같은데
저 식이 s가 1인 자리에는 $|-\rangle$가 되고 , s가 0인 자리에는 $|+\rang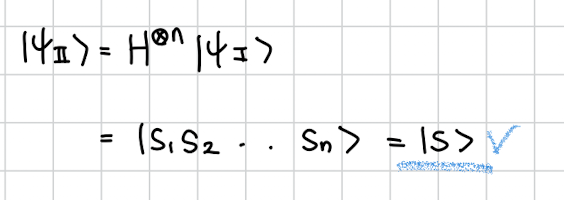le$가 되어서
저 식에 Hadamard를 적용하면 바로 우리가 찾던 S가 바로 튀어나온다고 한다.

너무 갑자기 S가 나와서 이해가 안될 수 있는데 왜 그러는지 알아보자.

일단 이 상태에서 언제 부호가 변하는가? 를 집중해서 봐야한다. 왜 s랑 같을까?

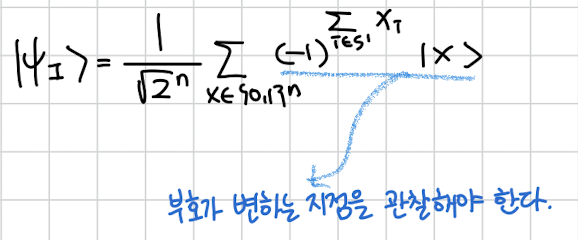
일단 부호가 변하는 곳이 $|-\rangle$가 되고 부호가 안변하는 곳이 $|+\rangle$가 되는 것 부터 이해해보자.

만약 다른 곳은 다 똑같고 3번째만 0과 1로 바뀌었다. 그런데 그와 함께 부호가 변하면 그 3번째 지점은 $|-\rangle$ 로 묶을 수 있다. !
만약 다른 곳은 다 똑같고 3번째만 0과 1로 바뀌었는데 그와 함께 부호가 그대로면 그 지점은 $|+\rangle$ 로 묶어낼수 있다. !

그래서 다 똑같은데 그 지점만 변하는 걸 쌍으로 집중해서 봐야한다.
우리가 가진 상태는 모든 n비트 상태가 다 있는 곳이다.
그래서 0000 부터 1111까지 모든게 다 있으니
우리는 첫번째 비트를 관찰하고 싶다면 1000 0000 의 부호를 비교해보고
두번째 비트를 관찰하려면 0100 0000을 봐도 되고 아니면 1101 1001 을 봐도 된다.그리고 다 관찰하면 각 비트가 $|+\rangle$ 인지 $|-\rangle$ 인지 알 수 있을 것이다.
의심이 들면 직접 $|+\rangle|-\rangle|-\rangle$를 전개해보고 우리가 예상한것처럼 1번째비트가 바뀌면 부호가 그대로고 2번째 3번째 비트가 바뀌면 부호가 바뀌는지 보면 된다.

그래서 부호가 바뀌는것 까진 확인했다면 왜 S가 나오는지 더 쉽게 이해할 수 있다.
n=5일때 예시를 봐보자.

저렇게 x1과 x2는 서로 첫번째 비트만 다르고 부호가 다르다.
그 뜻은 f(x1)과 f(x2)의 함수값이 서로 다르단 뜻이고 정확히 말해
f(x1)=0이여서 플러스 부호를 f(x2)=1이여서 마이너스 부호를 가진 것이다.
그런데 x1이 x2보다 1을 더 갖고 있다.
그래서 내적 값은 무조건 x1과의 내적값이 x2보다 1이 더 큰것이다. 그 뜻은 x1의 첫번째 1이 계산이 되었단 거다!
계산에 x1의 첫번째 비트가 포함되었단 것은
그 첫번째 인덱스가 S1에 속한단 뜻이다.
그 뜻은 s의 첫 비트는 1이란 뜻이다. 왜냐면 애초에 S1인 지점만 카운트 하고 S가 0인 지점은 보지도 않기 때문에.
그래서 부호가 변하는 곳에서는 S가 1이되고 부호가 안변하면 S가 0이된다 .

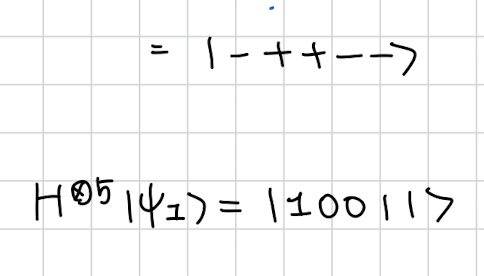
따라서 우리는 다음과 같이 $|-\rangle|+\rangle|+\rangle|-\rangle|-\rangle$ 가 결과로 나왔다면
그걸 Hadamard 만 씌우면 $|1\rangle|0\rangle|0\rangle|1\rangle|1\rangle$이 나오고 이게 바로 우리가 찾던 S라고 할 수 있다. 왜냐면 부호가 바뀌는 $|-\rangle$ 자리는 S가 1인 자리라고 확인했기 때문이다.

그래서 이렇게 간단히 n비트 string을 찾아낼 수 있다.

DJ랑 회로 자체는 똑같지만 개인적으로 왜 그런지 이해하기는 좀 더 복잡하다...

공부한거 정리라 틀린내용 많을 수 있음.