Deutsch-Jozsa algorithm

DJ 알고리즘은 다음과 같은 상황을 해결해줍니다.
예를들어 $f : \{0, 1\}^n \mapsto \{0, 1\}$ 같은 함수가 있다고 합니다.
그런데 이 함수는 딱 두가지 경우라고 합니다.
모든 값이 같은 상수 함수거나 , 절반은 0 절반은 1 인 balanced 한 경우요.
이 두 경우를 구분하기 위해서는 원래 생각대로라면
그냥 n비트의 절반을 구해보고 그것보다 하나 더 구해보면 되겠죠,,?

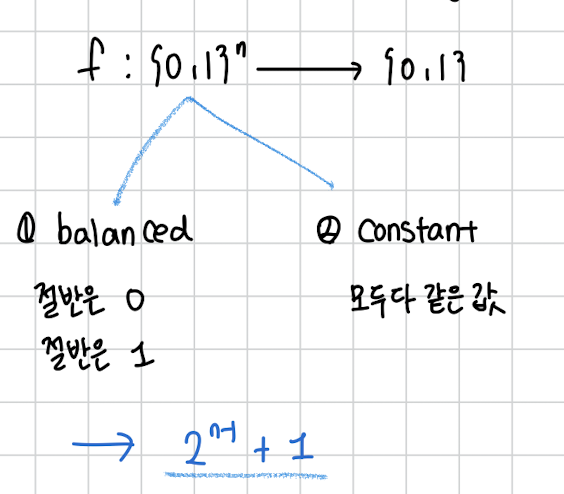
그래서 원래대로라면 $2^{n-1}-1$ 번 확인을 해야합니다.

하지만 퀀텀에서는 또 다시 단 한번으로 구분을 할 수 있습니다.

먼저 다음과 같은 회로를 먼저 이해해야합니다.
저번에 Deutschs 알고리즘 에서는 1비트 $|0\rangle$ 을 H에 적용했는데

이제는 n개의 $|0\rangle$을 H에 넣어서
n비트로 가능한 모든 superposition을 만들고 그걸 이제 $|-\rangle$와 함께 $U_f$에 넣습니다.

그러면 다음과 같이 되는데요 모든 가능한 n비트의 superposition은 변함 없는데 앞에 f(x)의 결과에 따라 마이너스 부호가 붙거나 안붙습니다.

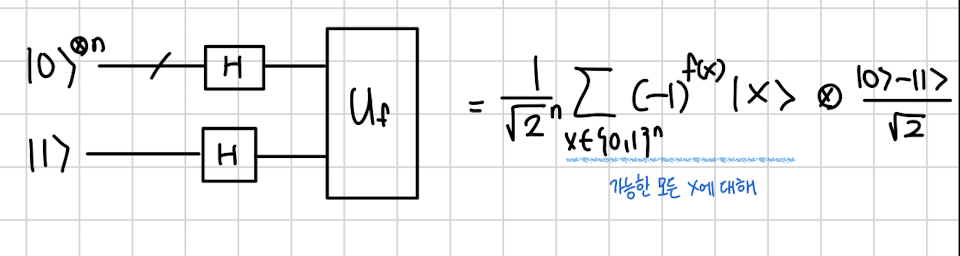
가능한 모든 x에 대해 f(x)의 값이 부호에 등장하는 상태죠

Deutsch-Jozsa 알고리즘은 여기서 H를 다시 한번 첫번째에 적용하고 측정합니다.

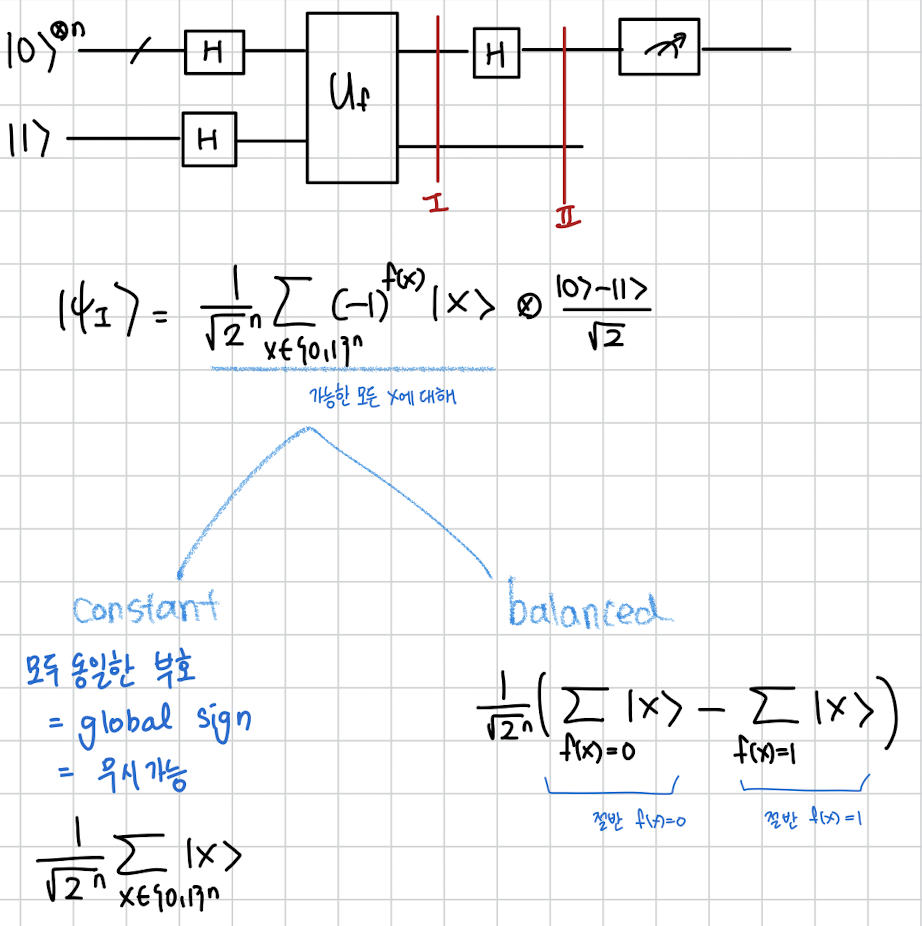
그러면 두개의 경우를 생각해볼 수 있습니다. 먼저 $f(x)$의 값이 모두 다 같은 constant의 경우 부호가 모두 다 같으니 global sign으로 생각되어질 수 있어 무시할 수 있게 됩니다.
만약 balanced하다면 $f(x)=0$ 인 경우와 $f(x)=1$ 인 경우가 딱 절반씩 나뉘게 될겁니다.

먼저 간단한 constant일 경우를 살펴보면

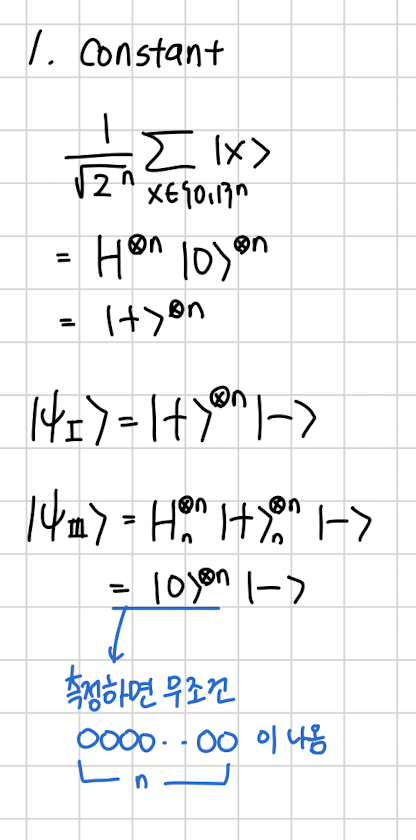
다음과 같이 항상 n 비트의 결과는 $|00000...000\rangle$ 이 나오는걸 알 수 있습니다.

이제 balanced 한 경우를 알아보면

이 경우에는 $|00000...000\rangle$ 은 무조건 나올 수 가 없습니다. 측정한 결과 어떤 임의의 값으로 측정되겠지만 그건 무조건 $|00000...000\rangle$은 아닙니다.

이유를 예시와 함께 더 설명해보면 다음과 같이 n=2인 경우를 생각해봅시다.

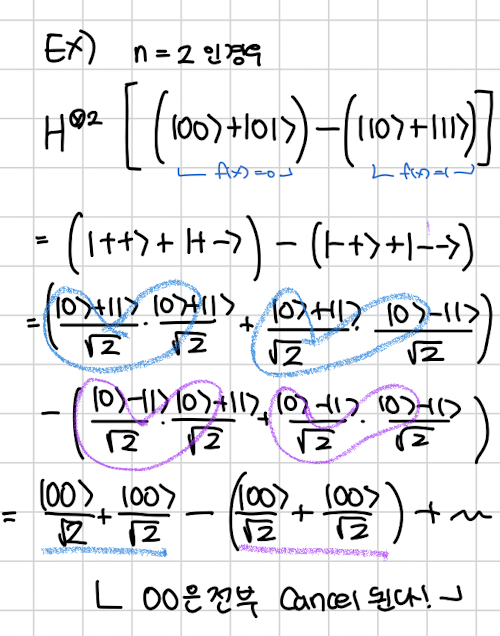
다음과 같이 $|00\rangle$ 상태는 왼쪽에서도 나오고 오른쪽에서도 나오는데 그 갯수와 부호가 동일해서 서로 동일한걸 뺄셈하니 삭제되는것을 알 수 있습니다.

이것과 동일하게 n 비트일때도 $|00000...000\rangle$은 왼쪽에서도 오른쪽에서도 동일하게 생성되고 그 둘을 빼게 되니 삭제되어서 절대 측정결과 나오지 않습니다.

결국 우리는 마지막 결과를 측정했을때 $|00000...000\rangle$ 가 나오면 constant
다른 값이 나오면 balanced라고 맞힐 수 있게됩니다.

이렇게 1번의 연산으로 둘을 비교할 수 있게 됩니다.
기존의 경우 2의 n-1 승 연산이 필요한거에 비하면 엄청난 효과라고 할 수 있습니다..

공부한거 정리한거라 틀린 설명 있을 수 있어용