Simon’s algorithm

Simons 알고리즘을 주기를 찾는 문제입니다.
다음과 같이 2 to 1 함수가 있다고 합시다.
2 to 1 이란건 항상 두 인풋이 쌍으로 같은 값을 가리킨다는 뜻입니다.

이때 헷갈릴 수 있는데 여기서 주기는 단순 덧셈이 아니라 bitwise xor 연산입니다.

8개 인풋이 있고 2개가 같은 값을 가리키는 주기가 있다고 하면 항상 4칸씩 떨어져야 하고 그런거 아닌가? 라고 생각할 수 있는데 xor이기 때문에 사실상 모든 값이 주기가 될 수 있습니다.

xor 성질을 이용해보면

만약 n=3일때 주기 a = 110이라고 합시다.

그러면
$000 + 110 = 110$
$110 + 110 = 000$

$001 + 110 = 111$
$111 + 110 = 001$

$010 + 110 = 100$
$100 + 110 = 010$

$011 + 110 = 101$
$101 + 110 = 011$

이렇게 쌍으로 각자 주기가 성립되고 a= 6으로 4보다 큰 값인 임의의 값인데도 주기가 될 수 있음을 보여줍니다.
아무튼 그래서 주기가 될 수 있는 가능성은 0을 제외한 $2^n-1$라고 할 수 있습니다.

원래 이 함수의 주기를 찾기 위해선 그냥 다 계산해보고 운좋게 같은 값을 가진 두쌍을 찾길 바라는 것이 최선입니다. 대충 $2^{n/2}$ 연산이 필요하다고 합니다.

Simons 이런 지수함수 복잡도를 n번으로 줄여줍니다.!

그리고 뒤에 나오는 Shors 알고리즘에도 많은 영향을 줍니다. Shors도 주기를 찾는 문제입니다..

Simons 알고리즘의 첫 단계입니다.
n개의 $|0\rangle$으로 superposition을 만드는 것 까지는 별개 없습니다.
특이한 점은 $f(x)$를 저장하는 곳이 기존에는 보통 1비트 $|0\rangle$ 이였는데
이제는 $|0\rangle^{n-1}$입니다.

당연한게 지금까지 DJ나 Deutsch 알고리즘에서는 $f(x)$의 결과가 $0$ 또는 $1$ 이였지만 지금은 2 to 1 이라서 총 $2^{n-1}$개의 서로다른 결과 값이 존재할 수 있기 때문에 $f(x)$을 저장하기 위해서는 $n-1$ 비트가 필요합니다.

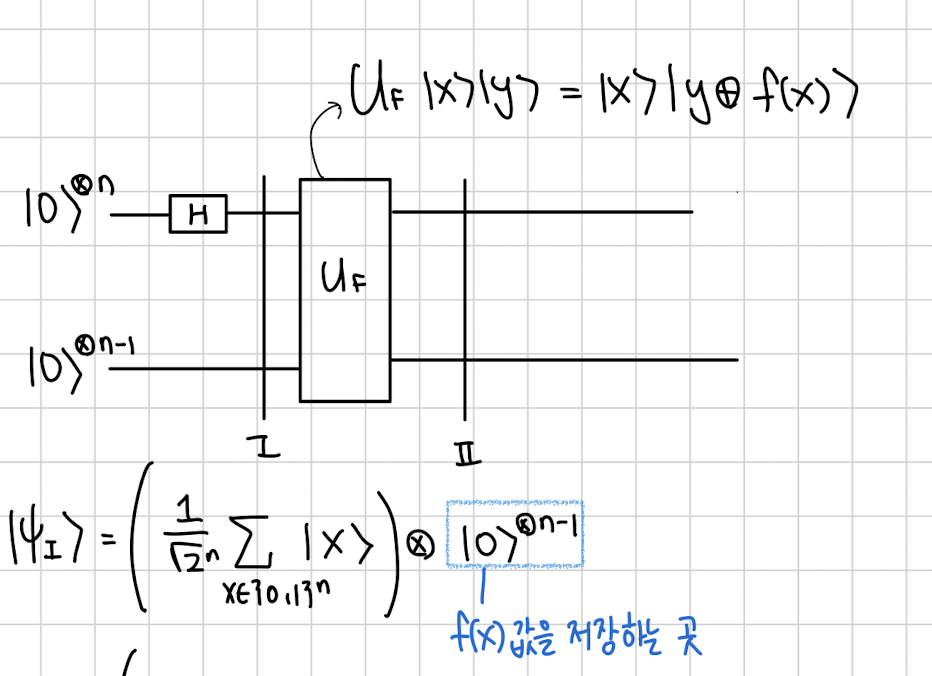
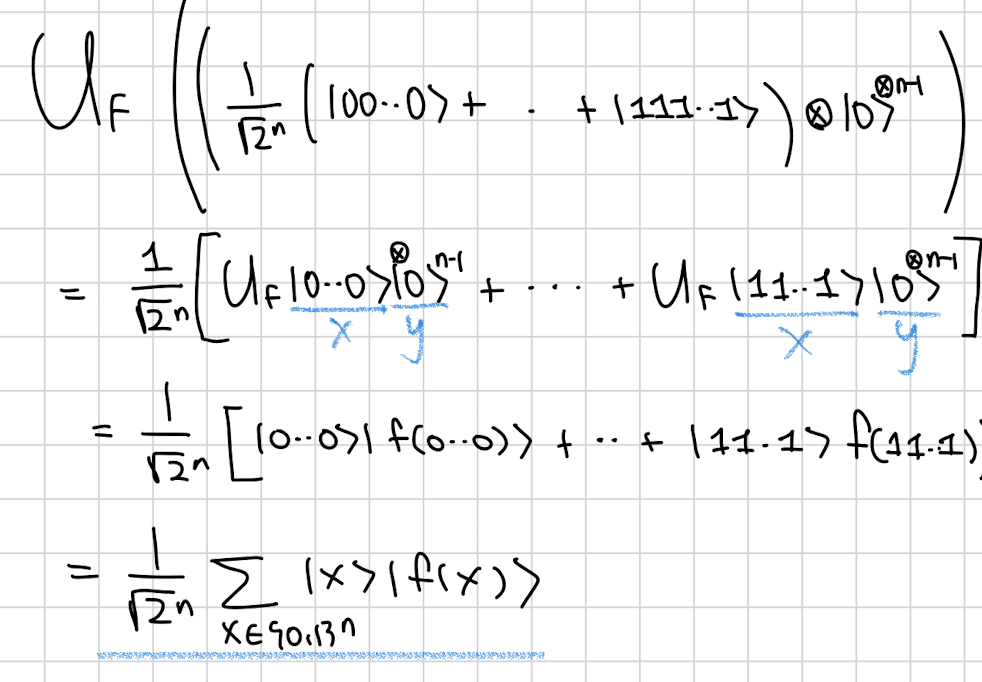
그래서 Uf를 지나고 나면 다음과 같이 모든 n비트 x에 대해서 그 결과 f(x)가 n-1 비트에 저장되어서 superposition상태로 나오게 됩니다.
여기까지는 기존과 비슷합니다.

여기서부터 중요한데
우리는 이미 모든 x가 짝꿍이 있고 그 짝꿍과 f(x) 값이 같단걸 압니다.

그래서 식을 다르게 쓸 수 있는데

이렇게 다르게 쓸 수 있습니다. $|x\rangle$와 $|x+a\rangle$ $f(x)$값이 같으니 저렇게 쓰는게 가능하고 근데 그렇게 하면 각 2개씩 중복되니 2로 나눠줍니다.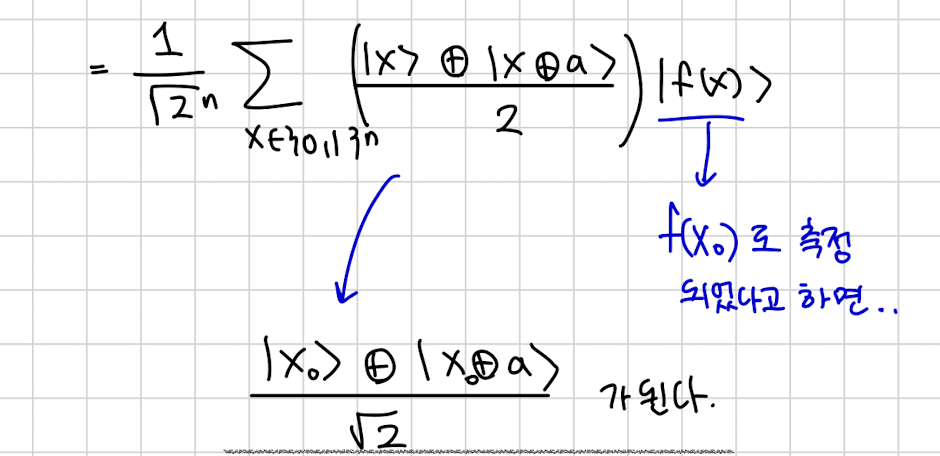

여기서 우리가 마지막 n-1 비트 즉 $f(x0)$을 측정해서 값을 확인했다고 칩시다.
그러면 그거에 해당하는 x는 뭘까요?
딱 두가지 가능성이 공존합니다. 왜냐면 2 to 1이기 때문에.
그래서 x는 저렇게 2개의 상태가 superposition 형태로 존재하게됩니다.
그래서 만약 측정하면 한번은 $|x_0\rangle$ 한번은 $|x_0+a\rangle$가 나올겁니다.
쉽게 이해해서 $f(x_0)$가 주어지면 아직 하나의 $x_0$로 특정할 수는 없고 아직 두개의 가능성이 공존한다고 생각하면됩니다.

여기서 그럼 이제 Hadamard를 씌워봅시다

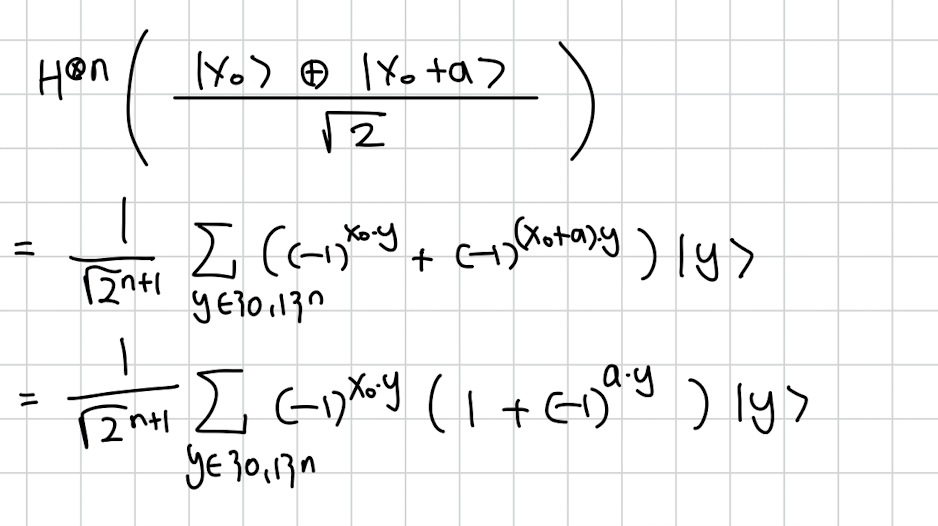
여기서 $|x_0\rangle$ 이 저렇게 $(-1)^{x_0 y}|y\rangle$ 로 펼쳐지는건 이전에 배웠던 BV알고리즘을 참고하면 이해하기 편합니다
간단히 설명하면 ,
$x_0$에 H를 씌웠고 그걸 전개한 겁니다. $H x_0$에서 $|-\rangle$ 인 지점에서는 부호가 변해야 하고 $| +\rangle$인 지점에서는 부호가 그대로여야 합니다. 그걸 만족시키도록 y의 부호를 조절하면 저렇게 됩니다. y가 $x_0$이 1인 지점과 얼마나 겹치는지 카운트 하고 겹치는 갯수가 홀수 짝수냐에 따라 부호가 달라지니까 부호가 변하는게 반영되게 됩니다.

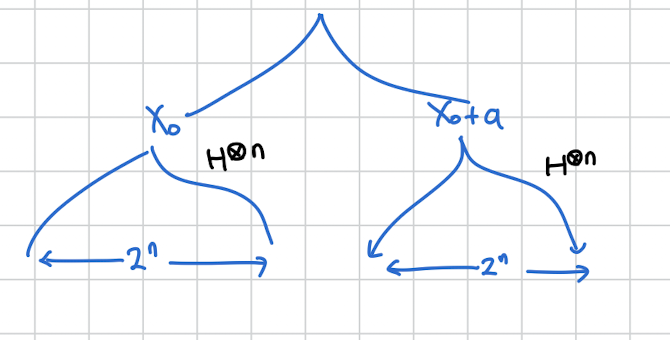
정리하자면 2개의 superposition 상태를 Hadamard를 이용해 다시 각각
2^n개의 superposition 상태로 바꿨습니다.

여기서 a와 y의 내적값은 mod 2 연산이라서 두가지 경우로 나눌 수 있습니다.
내적이 0일때만 생존하고 1일때는 제거되는걸 확인할 수 있습니다.

따라서 우리는 결국 a와 내적한 값이 0 mod 2인 y만 남습니다.

여기서 그럼 a를 구하는 법은,,,?
간단하게도
그냥 관측을 n번 이상 하면 됩니다.

그럼 y가 여러개 나올거고 그 측정한 y들은 모두 a랑 내적하면 0입니다.

그럼 우리는 n개의 방정식을 풀면 a를 가질 수 있을 겁니다.




근데 물론 조건은 우리가 구한 n개의 y가 서로 independent해야 하단겁니다.
예를 들어 y를 첫번째 측정한거랑 2번째 측정한거랑 4번째 측정한거랑 같다면,,, 서로 다른 n개의 방정식이 아니니까 풀리진 않겠죠...
보통 그래서 n번이 아니라 n+ m번 정도 한답니다.

아무튼
이렇게 선형 방정식을 세워서 a를 구할 수 있게 됩니다.