Deutsch’s algorithm

이렇게 간단한 함수 $f$가 있다고 할 때

$f(0) =f(1)$ 인지 $f(0) \neq f(1)$ 구분하는 법은 뭘까?

원래는 간단하게 $f(0)$ 과 $f(1)$ 을 둘다 구해서 비교하는 법 밖에 없습니다.

하지만 퀀텀컴퓨팅에서는 단 한번의 연산으로도 두 케이스를 구분할 수 있는데

바로 Deutsch’s algorithm 이 하려고 하는 일입니다.

일단 먼저 Uf의 방식을 설명하자면

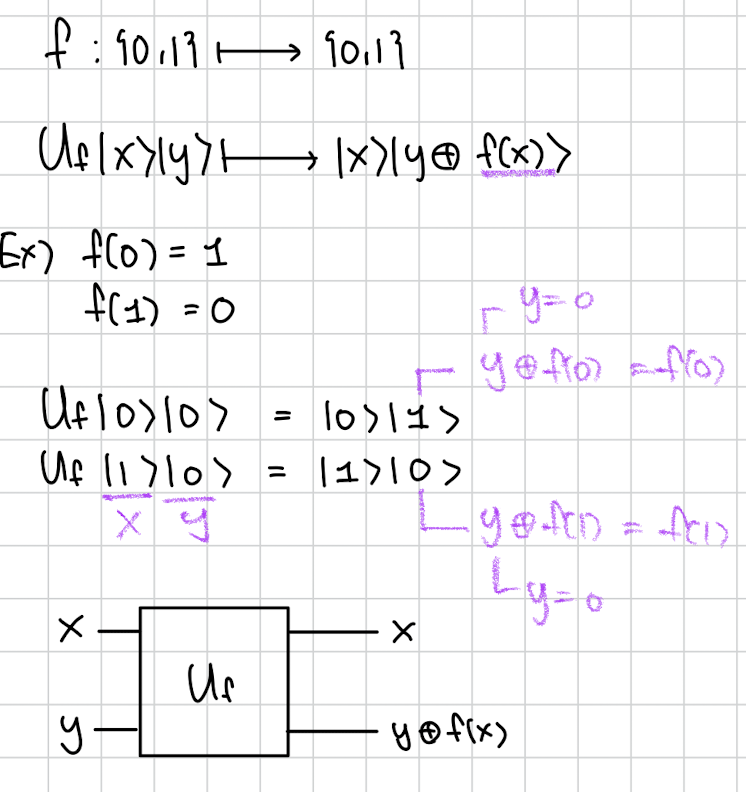
Uf는 마치 CNOT과 비슷하게 작용합니다. 첫번째 큐빗은 건들지 않고 두번째 큐빗에 f(x)의 결과를 더해 저장합니다. 이때 덧셈은 mod 2 덧셈입니다.
당연하게 생각하자면 y즉 두번째 큐빗이 만약 0 이라면 f(x)가 두번재 큐빗의 값이 되게 됩니다.
그래서 f(x)를 알기 위해서는 보통 y = 0 인게 좋지 않을까? 란 생각이 듭니다.

이제 이걸 0 에 적용하는게 아니라
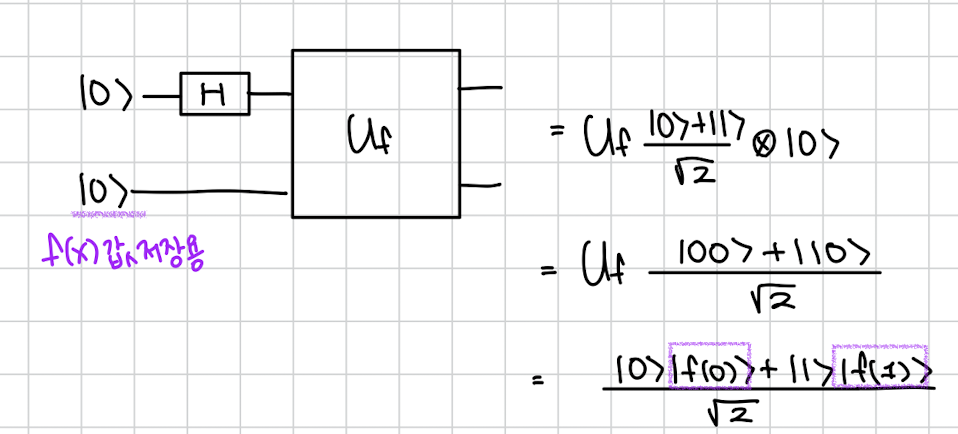
0에 H를 적용해 superposition을 만들어서 Uf를 적용하면?
우리는 f(0)과 f(1) 이 동시에 두번째 큐빗에 들어있는 superposition 상태를 만들 수 있게 됩니다.

이제 더 나아가 n비트에 H를 적용해서 n 비트 superposition 상태를 만들고 f(x)의 결과가 1비트이기 때문에 f(x) 저장용 1비트를 단거에 Uf를 적용해줍니다. 그러면 다음과 같이 모든 가능한 n비트의 f(x)값이 동시에 존재하게 되는 상태가 됩니다.

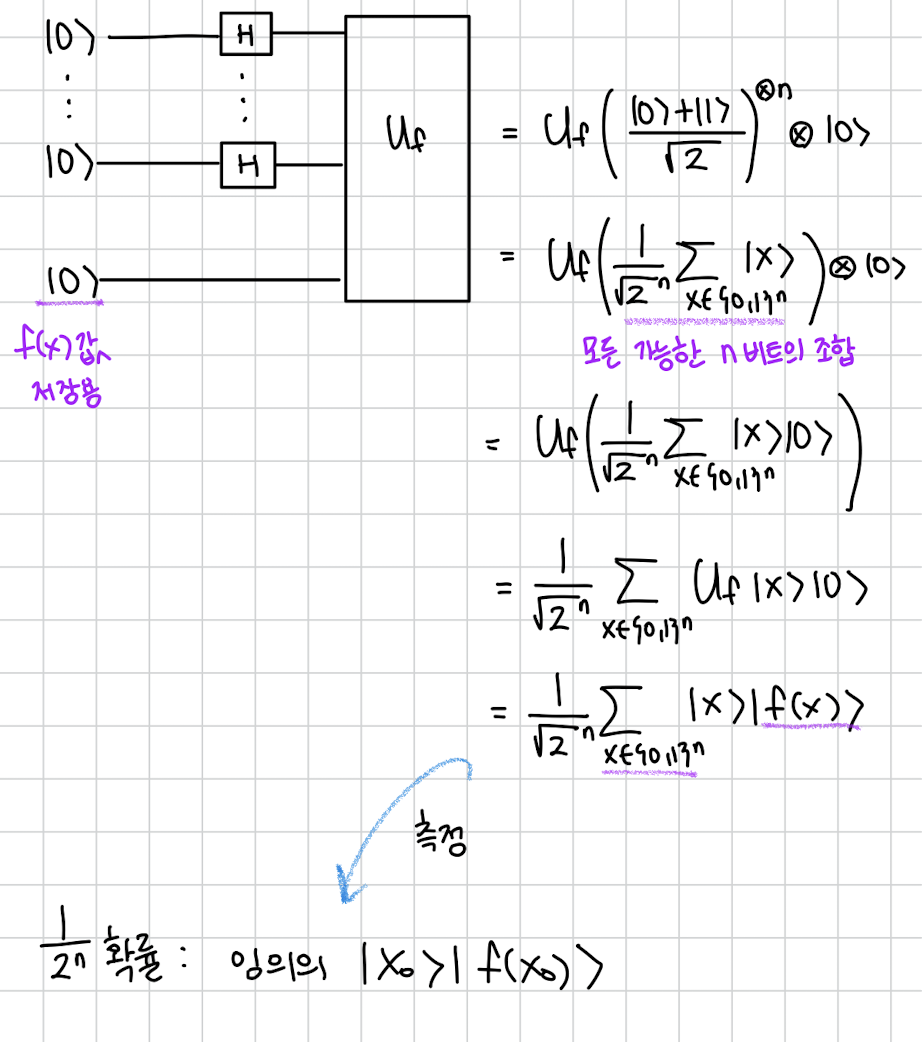
그런데 문제는 저 상태는 superposition 상태이고 측정을 하는 순간
저 중에 랜덤으로 하나의 상태로 붕괴됩니다. 측정해서 확인하지 못하는데 무슨 소용일까요?


그래서 Deutsch’s algorithm 에서는 다른 방식으로 생각하기로 합니다.

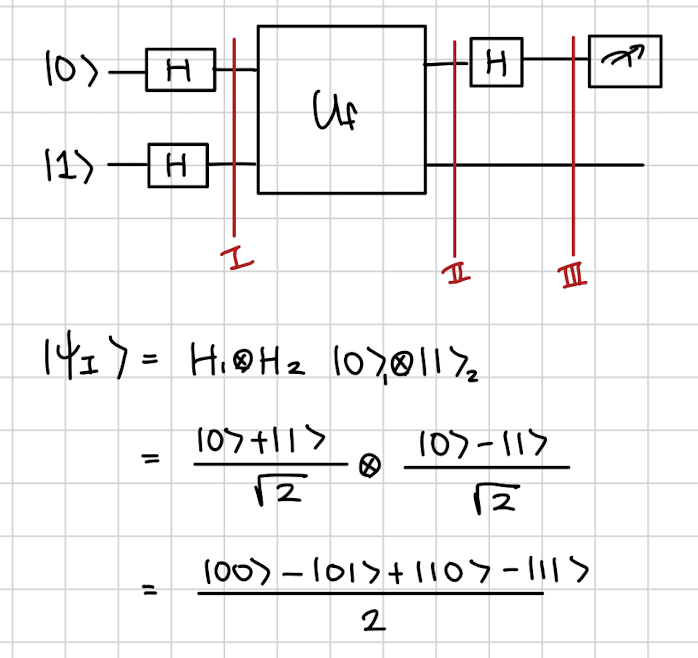
일단 저장용 비트에 $|0\rangle$ 을 넣는게 아니라 H를 이용해 $|-\rangle$를 넣습니다.

그 다음 연산을 계속하면 다음과 같이 됩니다.

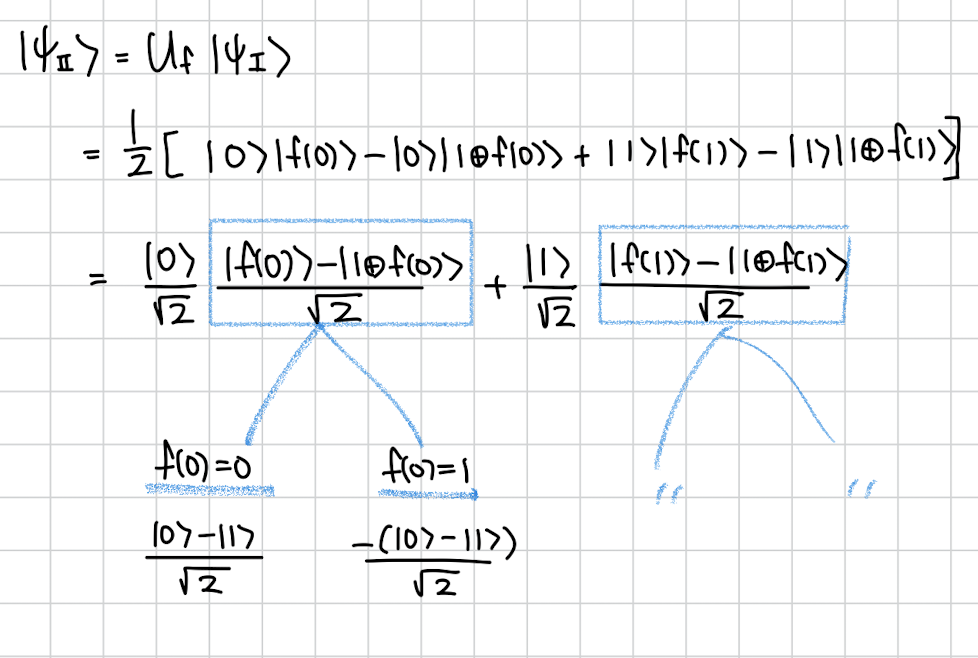
f(0) 의 값에 따라 -부호가 붙거나 안 붙습니다. 하지만 둘다 $|-\rangle$ 상태이긴 똑같기 때문에 우린는 이걸 묶어낼 수 있습니다.

묶어내면 다음과 같습니다. f(0) = 0이면 - 부호가 없고 f(0)=1이면 -부호가 생깁니다. f(1)에도 마찬가지..

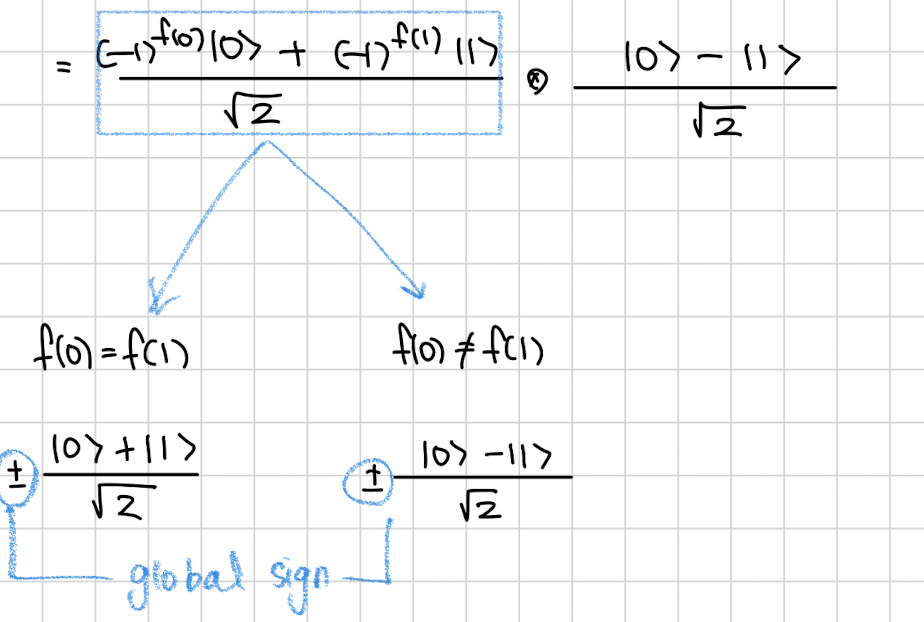
그런데 여기서 두 경우를 생각해볼 수 있는데 우리가 찾던 f(0) = f(1)이면? 두개의 부호가 같아서 global sign은 무시할 수 있으니 첫번째가 $|+\rangle$ 가 됩니다.
만약 두개의 부호가 다르다면?
$|-\rangle$ 가 됩니다.

다음과 같이 우리가 원하던 경우가 구분이 되기 시작합니다.
그럼 H로 +를 0으로 -를 1로 바꾼뒤 측정하면?

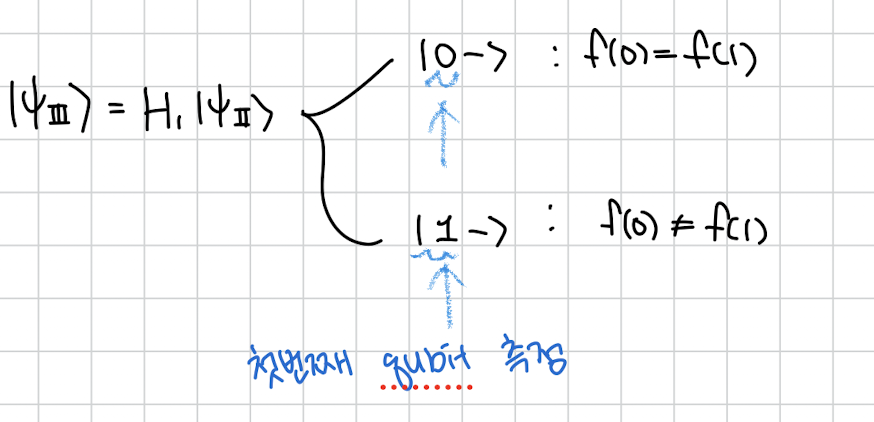
만약 측정결과가 0 이면 그뜻은 $f(0) =f(1)$ 이란거고
측정 결과가 1 이라면 $f(0) \neq f(1)$ 이란 뜻입니다.

이렇게 한번의 Uf 적용으로 두 경우를 구분할 수 있게 됩니다.

가장 간단한 알고리즘입니다.!



공부한거 정리라 틀린 내용 있을 수 있음..