Quantum Parallelism

Quantum Parallelism 은 모든 가능한 연산을 동시에 할 수 있다는 개념입니다.

클래식은 N 가지 방법이 있으면 차례대로 N번 시도해야하죠.

하지만 퀀텀컴퓨팅에서는 N가지 방법이 있다면
이걸 한번에 다 동시에 연산을 할 수 있습니다.

앞으로 나올 알고리즘들에서 매번 쓰이는 개념입니다.

$f(x)$ 라는 함수가 있습니다. 이 함수는 x를 받으면 함수값을 내놓습니다.

이 $f(x)$ 는 $U_f |x\rangle$ 로 구현이 된다고 생각합니다.

*자세한 Uf 구현은 뒤에 배웁니다.

그리고 이제 우리가 배웠던 Hadamard 게이트를 0에 적용한 결과들을 생각해볼 수 있습니다.

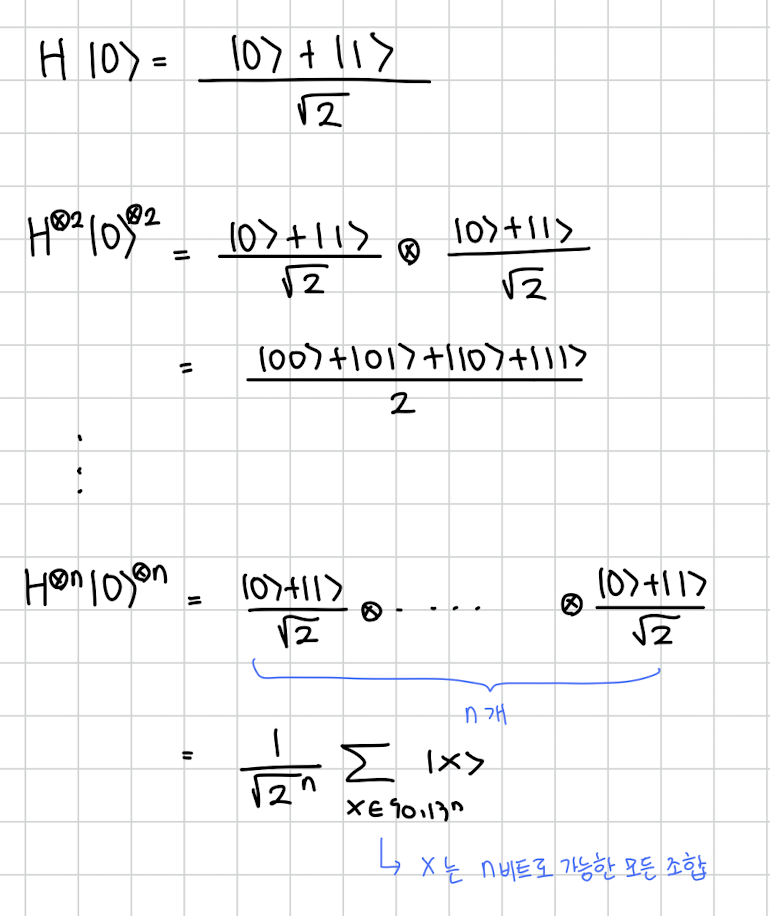
1비트에 H를 적용한 결과는 $|0\rangle$과 $|1\rangle$ .
2비트에 H를 각각 적용한 결과는 $|00\rangle |01\rangle |10\rangle |11\rangle$
.
.
.
.
n비트에 H를 각각 적용한 결과는 그럼 n비트로 만들 수 있는 모든 가능한 x가 superposition상태로 더해져서 나오게 됩니다.
간단하게 생각해서 0 비트가 H를 적용하면 0과 1로 쪼개지고
그런걸 총 n개 가지고 있다고 하면
0과 1로 만들 수 있는 모든 가능한 n비트 결과가 나오게 될거에요.

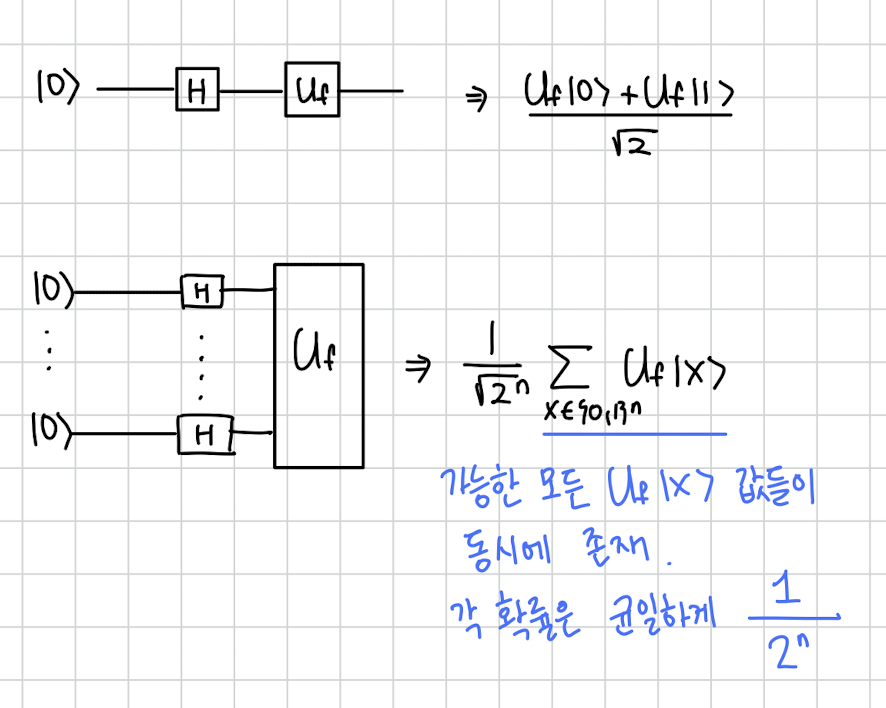
그림으로 하면 이렇게 됩니다.
첫번째 그림에서는 Uf의 인풋이 1비트겠죠.
마지막 그림에서는 Uf의 인풋은 n비트이구요.

저런식으로 n비트의 모든 가능한 Uf 적용값을 한번에 동시에 계산할 수 있습니다.

물론 측정을 하면 저 중에 한개의 결과만 볼 수 있겠죠.
저 모든 경우 중 한 상태가 측정될 확률을 동일하게 $\frac{1}{2^n}$입니다.

비록 한 상태만 랜덤하게 측정할 수 있더라도 모든 계산결과가 균등한 확률로 담긴 superposition 상태를 만들 수 있다는건 classical 컴퓨터와 비교했을 때 엄청난 차이입니다. !

공부한거 정리라 틀린 설명일 수 있어요..