Shor’s algorithm

이번에는 Factoring 과 관련된 알고리즘입니다.
알고리즘 자체는 그냥 주기를 찾는거지만 이걸 이용해서 큰 수를 Factoring할 수 있습니다.

저번에 Simons 알고리즘이 한 $f(x_0)$를 관측했을 때 가능성이 있는 $x$가 두가지가 있어서 그 두 상태가 superposition 상태로 존재하게 된다는 걸 이용했는데 그 개념을 여기서도 이용합니다.

지금까지 배운거에 비해 엄청 복잡하고 Quantum Fourier Transform 개념도 나옵니다.

Shors 알고리즘은 주기 r을 찾는 알고리즘입니다.

$f(x) = b^x \mod N$ 인 함수가 있습니다.

이 함수에서 $f(x) = f(x + r)$ 가 성립하는 주기 r을 찾는게 목표입니다 .

$b^x \mod N = b^{x + r} \mod N$ 이 식을 변형하면

$b^r \mod N = 1$ 이렇게 되어서
결국 1이 되게 하는 r을 찾는게 목표입니다.

여기서 $N$은 정수이고 이걸 표현할 수 있는 최소의 비트수를 $n_o$이라고 합시다.

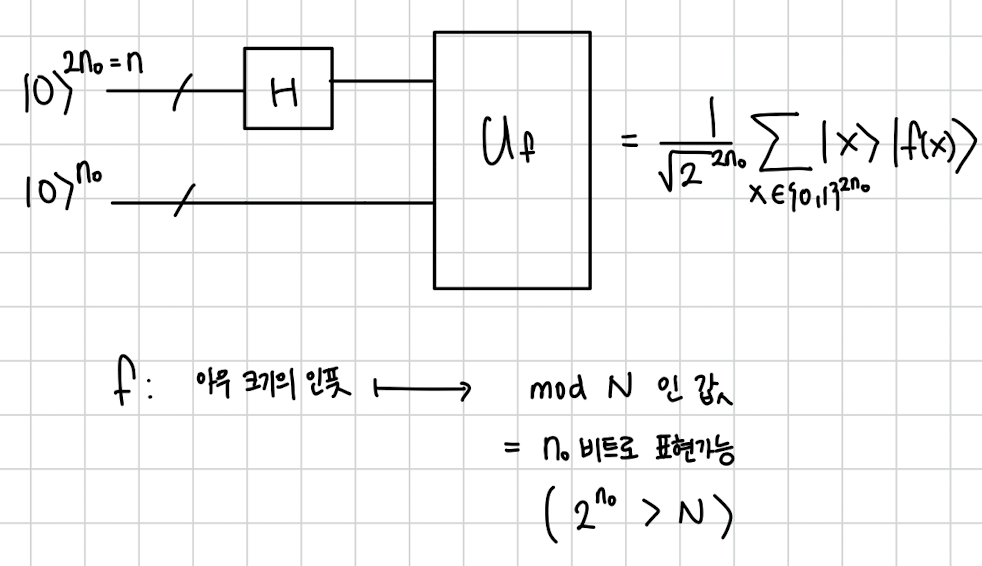
그림과 같이 첫번째에 $2n_0$비트를 넣습니다. 그리고 밑에는 $n_0$ 비트를 넣습니다.
왜 두배를 넣는지는 나중에 이유가 나옵니다. 밑에 $n_0$인 이유는 함수값 $f(x)$이 mod N 값이므로 N을 표현할 수 있는 $n_0$비트가 필요합니다.

편의를 위해 앞으로 $2n_0 = n$이라고 표기 하겠습니다.

그리고 하던대로 H로 n비트의 superposition을 생성하고 그걸 Uf에 넣으면
n 비트의 모든 경우에 대해서 그 함수값이 두번째 칸에 저장된 상태로 superposition이 생성됩니다.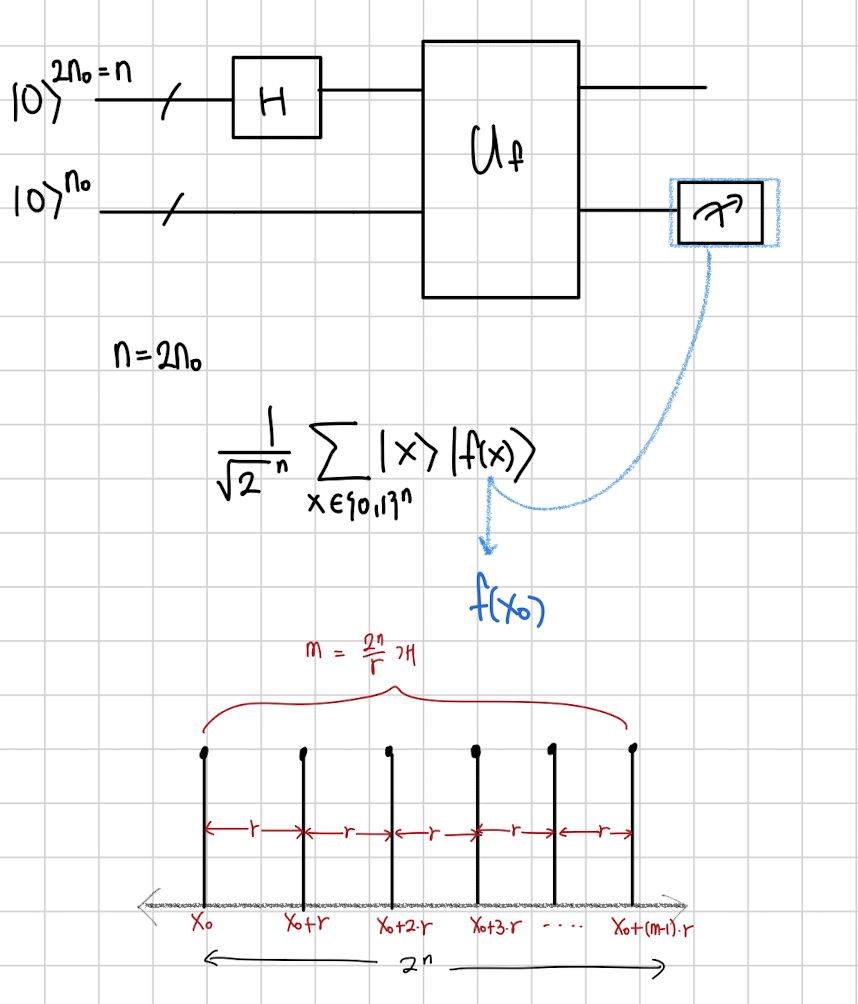
여기서 이제 두번째칸을 측정한다고 합시다. 그럼 임의의 $f(x_0)$이 나올것입니다.
이전 Simons 알고리즘을 떠올리면 가능한 $x$의 값이 2개라서 첫번째 칸에서 2개의 경우의수를 담은 상태가 생성되었습니다. .

과연 여기서는 하나의 $f(x_0)$ 당 몇개의 $x$ 가 그럼 가능할까요?

정답은 전체 크기에서 주기로 나눈 $m = \frac{2^n}{r}$ 개가 됩니다.

그럼 우리는 첫번째칸에 이제 2개가 아닌 $m$개의 경우가 동시에 담겨있는 superposition을 얻게 될것입니다.

여기서 측정때마다 달라지는건 $x_0$값입니다. 이 $x_0$과 r을 떨어뜨릴 수만 있다면 계속 측정하면서 랜덤에 맡기지 않아도 될 것입니다. 그래서 우리의 목적은 $x_0$을 앞으로 떼어내는 것이고 그걸 위해서 Quantum Fourier Transform을 사용할겁니다 .

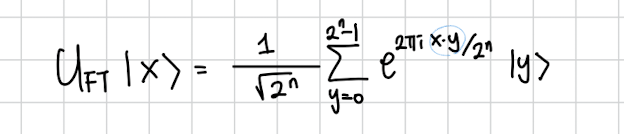
이게 퀀텀 푸리에 변환인데 그냥 n 비트 길이의 x를 모든 가능한 $2^n$개의 superposition 형태로 퍼트린다고 생각하면 됩니다. 거기서 진폭을 결정하는건 x와 y의 곱셈값입니다.
이걸 구현하는건 나중에 더 자세히 배울 수 있습니다.
이걸 우리의 원래 상태에 적용하면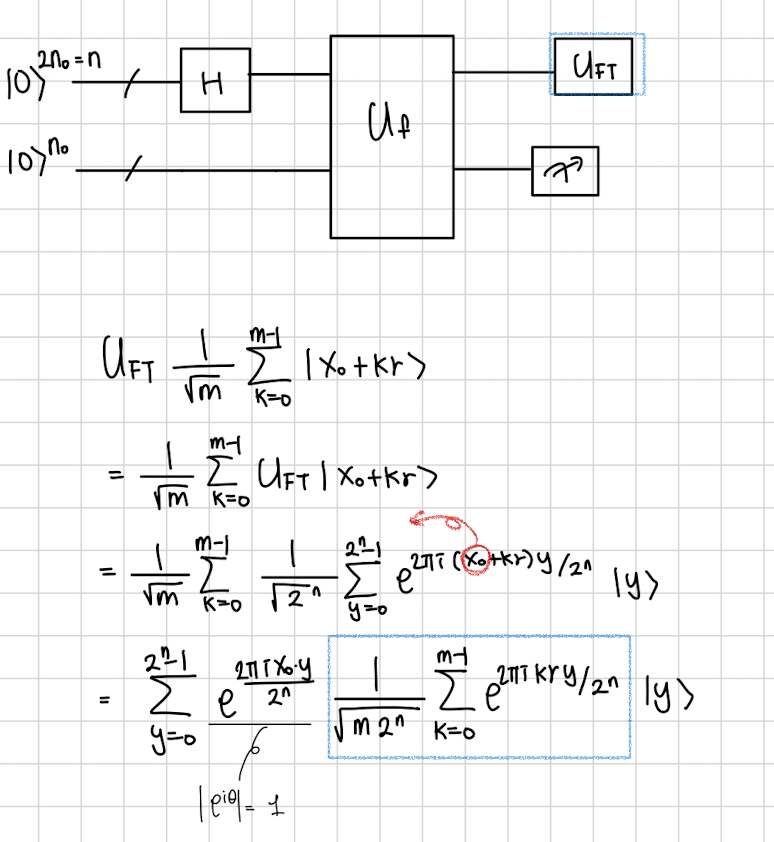
이렇게 됩니다. 여기서 성공적으로 $x_0$을 앞으로 뺄 수 있었고
어떤 임의의 $y_0$을 측정할 확률은 저 파란네모의 absolute 값을 제곱한것과 같을 것입니다.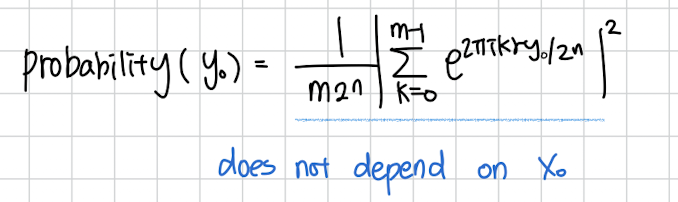
이 확률값은 $x_0$에 의존하지 않고 측정된 $y_0$에 따라 달라지는 걸 알 수 있습니다.

어떤 $y_0$에서 확률이 높을까요??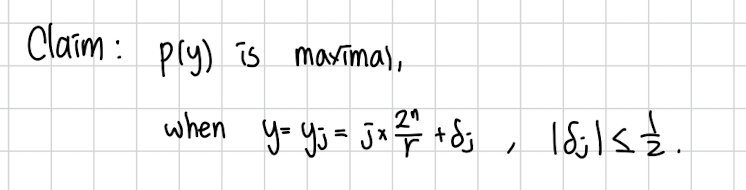
이 알고리즘의 주장은 이것입니다. $\frac{2^n}{r}$의 정수배 근처에서 제일 y의 확률이 높다는 것입니다.
그렇단 뜻은 여러번 100번 정도 y를 측정하고 본다면 특정 부분에 y가 집중되어있을 것입니다. 그럼 그곳은 $\frac{2^n}{r}$의 정수배 언저리 란 뜻입니다.

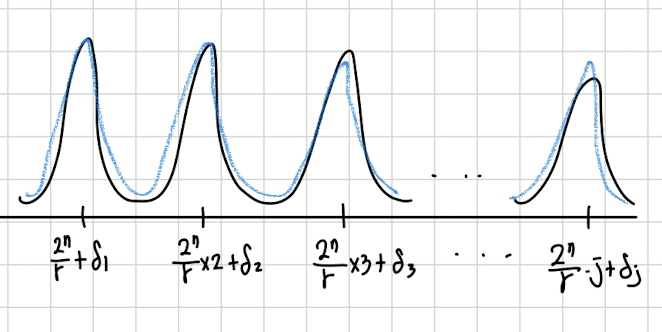
그림으로 보면 대충 이런식으로 분포한다는 뜻입니다.

이걸 증명하는 것은 다음과 같습니다. 우리가 구한 확률에 $y_j = j \cdot \frac{2^n}{r} + \delta_j, \quad |\delta_j| \leq \frac{1}{2}$ 를 대입해 보면 됩니다.

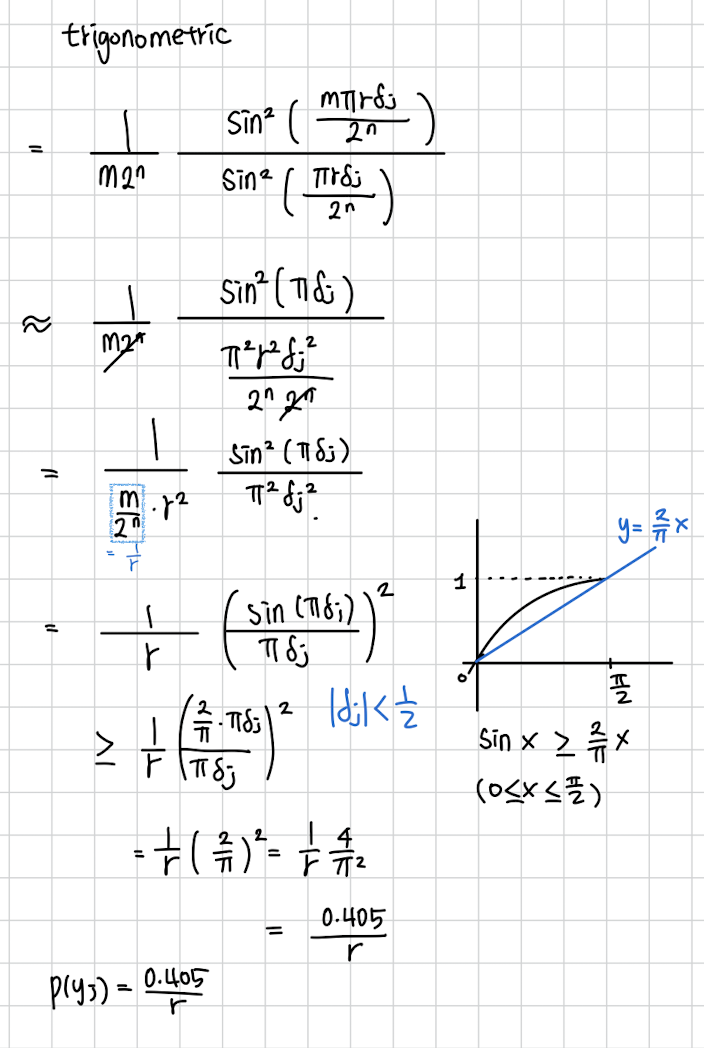
음 결론만 보면
$y_j = j\cdot \frac{2^n}{r} + \delta_j, \quad |\delta_j| \leq \frac{1}{2}$ 를 대입한 결과
$P( y_j) =\frac{0.405}{r}$ 입니다.

그런데 우리는 이런 $y_j$가 적어도 r-1개는 있습니다.

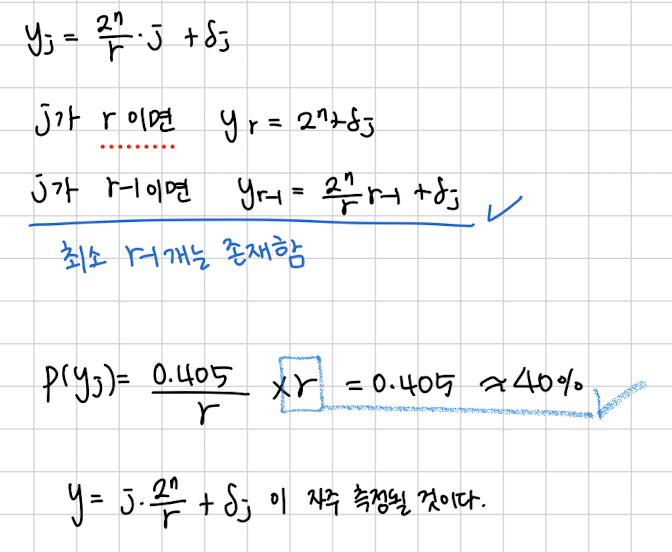
그렇다면 결국 우리가 임의의 y를 측정했는데 걔가 $y_j = j\cdot \frac{2^n}{r} + \delta_j, \quad |\delta_j| \leq \frac{1}{2}$ 여기에 속할 확률이 40프로나 된다는 뜻입니다.!

우리는 일단 우리가 측정한 y가 저런 값이라는걸 알 수 있습니다.
우리는 이걸 이용해서 r을 찾을 수 있습니다.

하지만 r을 정확히 찾는 법은 또 쉽지는 않습니다.
연분수 전개를 통해 찾아야 합니다.

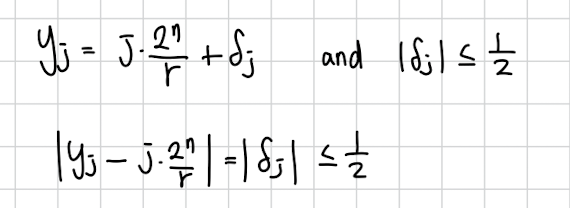
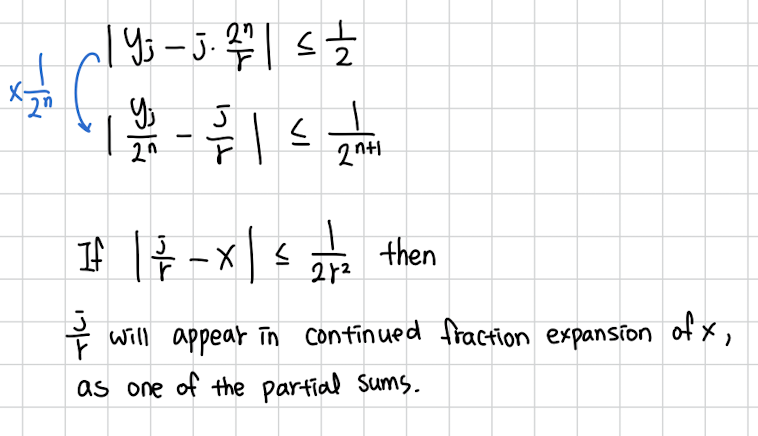
다음과 같은 정리를 사용할건데 저 조건이 만족하면 x 의 연분수 전개에 우리가 찾던 $\frac{j}{r}$ 이 등장한다는 소리입니다.

조건이 만족하는걸 증명하면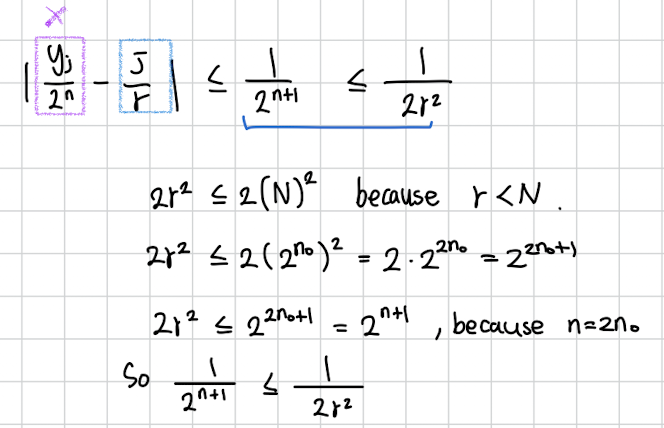
드디어 여기서 왜 우리가 처음에 두배인 $2n_0$비트를 사용했는지 나옵니다.
이 조건을 만족해서 연분수 전개하기 위해 두배 비트를 사용했던 것입니다....

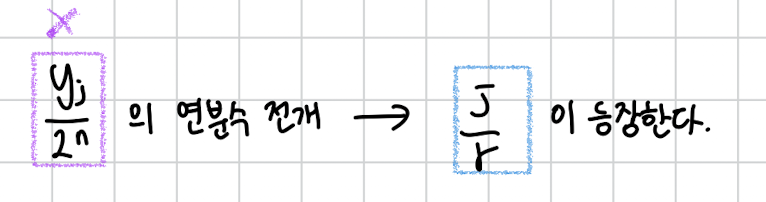
아무튼 그래서 y를 측정하고 그걸 n이 뭔지는 우리가 아니까 그걸로 나눠서 연분수 전개해서 partial sum을 하나하나 보다보면 $\frac{j}{r}$ 이 등장합니다.

실제 연분수 전개해보는 연습문제와 이게 어떻게 Factoring에 사용될 수 있는지는 다음 편에서 설명하겠습니다..

공부한거 정리한거라 설명 틀린거 많을 수 있어요