01-3 지도학습 개요

어제는 지도학습이라는 행위가 무엇인지, 종류에는 어떤 것이 있는지, 그 가운데 '관심'의 역할은 무엇인지에 대해 이야기해보았다.

첫 날에 지도학습은 supervised learning이라고 했다.

super(over) + vise(see) = 모든 상황을 지켜보다

그리고 어제는 지도학습을 통해 '예측'이라는 가치를 창출한다고 하였다. 예측은 아직 오지 아니한(未來) 대상에 대한 것인데, 그럼 위에서 말하는 '모든 상황'은 미래를 포함한다는 뜻인가? 그 말은 미래를 볼 수 있다는 뜻인가? 아니다.

지도학습을 진행하려면, 주어진 데이터셋의 한 쪽을 미래의 사건으로 치부한다는 전제가 필요하다. 이미 데이터셋 자체가 어원적으로 datum(주어진 것), 과거의 산물이지만 말이다. 그러면 이런 이질감을 어떻게 감당할 수 있겠는가? 너도 나도 그것이 과거의 사실임을 아는데, 그걸 아직 일어나지 않은 셈 치자고?

배우는 건 우리가 아니니까

우리가 이미 모든 데이터를 아는 채로 그 데이터셋에 대해 지도학습을 한다면 그건 문제다. 확보한 모든 데이터를 감안하여 어떤 압축된 정보, 예측을 내놓은 것이니, 앞으로 새로운 데이터를 확보하기 전까진 우리가 내놓은 예측이 괜찮은 건지 아닌지 알 수가 없다.

그리고 아무리 미래에 대한 진술이라도 그것이 가치를 발휘하려면 '그럴싸' 해야한다. 예측의 가치는 무언가에 의존할 수밖에 없는 인간의 나약한 본성에서 비롯되었다고 했다. 그럼에도 인간은 생각하는 동물이기에 너무 말도 안 되는 예측에는 가치를 느끼지 못한다. 심지어는 혐오감을 가지는 사람들마저 종종 있다. 이것은 예측에 대한 근거의 문제다.

이런 문제를 해결하기 위해 우리가 학습시킬 지도학습 알고리즘이 실제로 미래를 예측한 이력이 있음을 내세울 수 있다면 좋겠지만, 거기에는 시간이 많이 들 것이다. 1년 뒤의 대상에 대해 예측을 하는 알고리즘의 성능을 증명하려면 최소한 1년이 필요하다. 심지어 한 번 맞아떨어졌다고 누가 믿어주겠는가? 이렇게 말하며 빈정대어도 할 말이 없다.

고장난 시계도 한 번은 맞아~

일반화 성능, 무작위

그래서 지도학습 알고리즘의 성능은 '일반화가 얼마나 잘 되었느냐'에 좌우된다. 1년 동안 얼마나 공들여서 학습을 시켰든, 학습의 가치는 1년 뒤에 일어날 일을 얼마나 정확하게 예측했는지에 좌우된다는 것이다. 예측에 대한 갈망에 의해 예측을 해주는 알고리즘을 만들었는데, 그것이 얼마나 예측을 잘할지에 대해서도 예측하고 싶다는 또다른 갈망이 생긴다. 갈망의 연쇄, 끝없는 인간의 나약함이다.

그러나 결국 미래를 알 수가 없으니, 눈 가리고 아웅을 할 수밖에 없다. 과거를 미래인 셈 치는 것이다. 다행히 우리는 이 사실을 알지만, 지도학습 알고리즘은 모르니까 속아 넘어가줄 것이다. 다만, 어떤 과거를 미래로 치부할 지 고를 때에는 조심해야 한다. 그 선택에 의해 학습의 결과가 좌우되어서는 안 되지 않겠는가.

그러면 그 선택이 어떻게 결과에 영향을 미칠 지는 어떻게 아는데? 아무도 모른다. 그러니까, 100개의 데이터 중 어느 20개를 미래에 일어날 일로 치부하고 나머지 80개만 이용해 학습을 했다고 하자. 하필 그 80개가 전혀 일어나지 않을 법한 사건에 대한 데이터라면? 80개에 대한 성능은 괜찮을지라도, 나머지 20개로 테스트했을 때는 성능이 좋지 않은 것으로 나올 것이다.

이 경우, 성능이 좋지 않은 원인이 '80개의 데이터가 비현실적'이라고 정확히 콕 집어낼 수 있겠는가? 애초에 어떤 데이터가 얼마나 비현실적인지 가려내는 것 자체가 자연의 섭리에 도전하는 행위라, 우리 인간은 데이터를 나누는 기준을 오로지 '무작위'에 의존할 수밖에 없다. 무언가를 위해(爲) 만들어낸 것(作)이 아님(無). 그것을 최대한 확보하는 길만이 과거를 미래로 속인다는 이질감을 극복할 유일한 방법일 것이다. 그 방법들은 추후에 소개해볼 것이니, 오늘은 '무작위로 데이터를 둘로 나누어 한 쪽만을 이용해 지도학습을 하여 성능을 측정하고, 나머지 한 쪽으로도 성능을 측정해 둘을 비교해본다'는 것만 이해하면 되겠다.

적절히 잃고, 적절히 얻는다

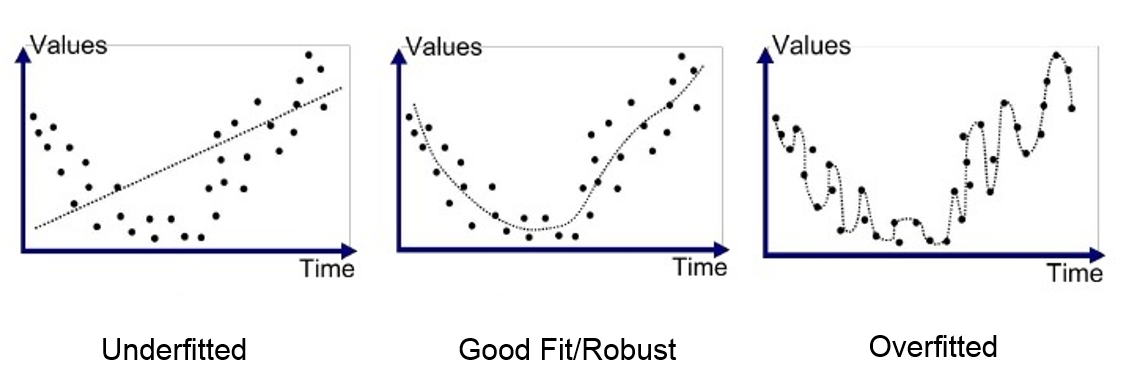
지도학습은 수많은 데이터를 압축해서 작은 정보를 얻어내는 행위라고 했다. 어제의 이 사진처럼, 아무 것도 잃지 않으려 했다간 아무 것도 얻지 못한다.
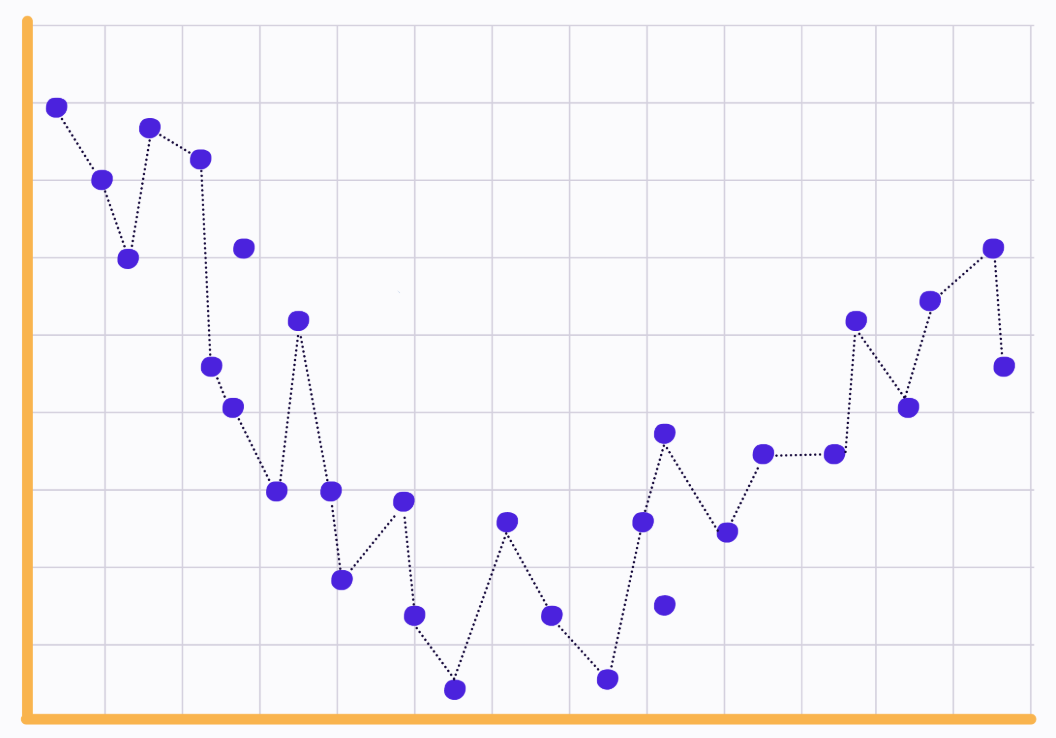[이미지 출처 (클릭)]

이런 경우를 과대적합(Overfitting)이라고 한다. 말그대로 점에 과하게 적합하도록 선을 그렸다는 뜻이다. 위의 사진을 정확히 이해하려면 지도학습의 과정을 비유적이지만 천천히 살펴볼 필요가 있다.

1. 주어진 데이터셋 D를 둘로 나눈다 : 훈련셋, 테스트셋
2. 훈련셋의 데이터만 그래프에 점으로 찍는다.
3. 그 점들을 이용해 나름의(그럴싸한) 추세선을 도출한다.
4. 처음 찍은 훈련셋의 점들만 지운다.
5. 테스트셋의 점을 새로 찍어 기존의 추세선과 비교하여 일반화 성능을 평가한다.

위 그림은 1~5번 중 어떤 과정에서 촬영했다고 보면 될까? 3번을 행한 직후라고 보면 되겠다. 훈련셋의 데이터포인트와 그것을 이용해 도출한 추세선인 것이다. 5번까지 다 해보지 않았는데 학습의 성능을 과대적합이라고 결론지었다. 사실 이는 논리적으로 검증하지 않은 결론이다. 그럼에도 많은 교육자료에서 아래처럼 가르친다.

[이미지 출처 (클릭)]

왼쪽부터 과소적합(훈련셋의 점들을 추세선이 적당하게 설명해내지 못함), 적당함, 과대적합 순이다. 이렇게 가르치는 이유는 누구나 '적당한' 추세선이 어느 쪽인지 그림만 봐도 이해가 되기 때문이다. 그러나, 우리가 머신러닝을 통해 다루는 데이터셋은 이런 2차원 그래프에 표현하지 못할 정도로 복잡하다. 그런 경우에는 어떻게 할 것인가? 우리가 수집한 데이터셋도, 알고리즘이 도출한 추세선도 모두 시각적으로 볼 수 없을 때에는?

오차

그 알고리즘이 어떤 데이터셋에 대해 내린 예측이 얼마나 정답에서 벗어났는지를 표현하는 '오차(Error)'를 이용한다. 오차는 우리가 피하고자 하는 상황을 숫자라는 정보로 압축해서 표현한 수치다. 비슷한 느낌으로 손실(Loss)이나 비용(Cost)으로 표현되기도 한다. 더 잘 예측할 수록, 오차는 줄어드니까 성능에 반대되는 값이라고 해석할 수 있다.

[이미지 출처 (클릭)]

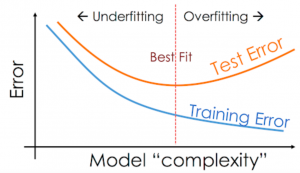
그래서 좀 더 논리적으로 과소적합, 과대적합을 판단하려면 1번~5번을 모두 수행한 후 위와 같은 오차(Error) 그래프를 다양한 알고리즘 조건 하에 도출해봐야 한다. 가로축의 모델 복잡도는 현재로서는 어떤 조건이라고만 생각하자. 크게 왼쪽, 중간, 오른쪽으로 나눠서 훈련셋과 테스트셋에 대한 오차의 차이에만 주목해보자. 왼쪽은 차이가 작고, 중간은 그 값이 조금 커졌다가, 오른쪽은 차이가 매우 커진다. 그러면 훈련셋과 테스트셋의 차이가 제일 작은 왼쪽이 가장 적합한 지도학습 알고리즘인가?

왼쪽은 두 경우의 차이가 작지만 두 경우 모두 오차가 크다. 즉, 아무리 일관적이더라도 예측을 잘 하지 못하면 의미가 없는 것이다. 비유하자면, 꾸준히 틀린 답을 내는 학생이다. 오른쪽은 훈련셋에 대한 오차가 작지만 테스트셋에 대한 오차는 크다. 아무리 훈련셋에 대해 예측을 잘해도, 결국 테스트셋에서 발휘하지 못하면 일반화 성능이 안 좋은 것이다. 이 경우는 비유하자면, 기출문제만 외워서 정작 시험 점수는 낮게 받는 학생이다.

그래서 우리는 중간을 택한다. 훈련셋에 대한 예측보다 테스트셋에 대한 예측이 '적당히' 안 좋은 조건, 그리고 훈련셋과 테스트셋에 대한 예측 오차가 모두 '그리 높지 않은' 조건을 찾는다. 그 기준은 명확하지 않지만, 적어도 양극단은 아닐 것임을 직관적으로 생각해볼 수 있다.

이번 시간에는 지도학습의 핵심인 일반화 성능과, 그것을 판단하는 기준인 오차에 대해 이야기 해보았다. 그러나 일반화를 향한 길은 멀고도 험하며, 어떤 상황에서 어떤 데이터를 어떤 알고리즘으로 분석하느냐에 따라 적당한 기준을 설정하기가 힘들 것이다. 그리고 이 과정에서 아직 논의되지 않은 '모델의 복잡도'에 대해서 다음 시간에 이야기해야 한다. 그렇게 지도학습에 대한 개요를 마치면, 그 이후에는 본격적으로 알고리즘들에 대해 다뤄보겠다.