[Boostcamp AI Tech] 1주차

강의 학습 내용

1. 경사하강법

• 미분 : 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구

최근에는 컴퓨터가 계산해줄 수도 있음.

• 미분을 통해서 접선의 기울기를 알 수 있음.
  
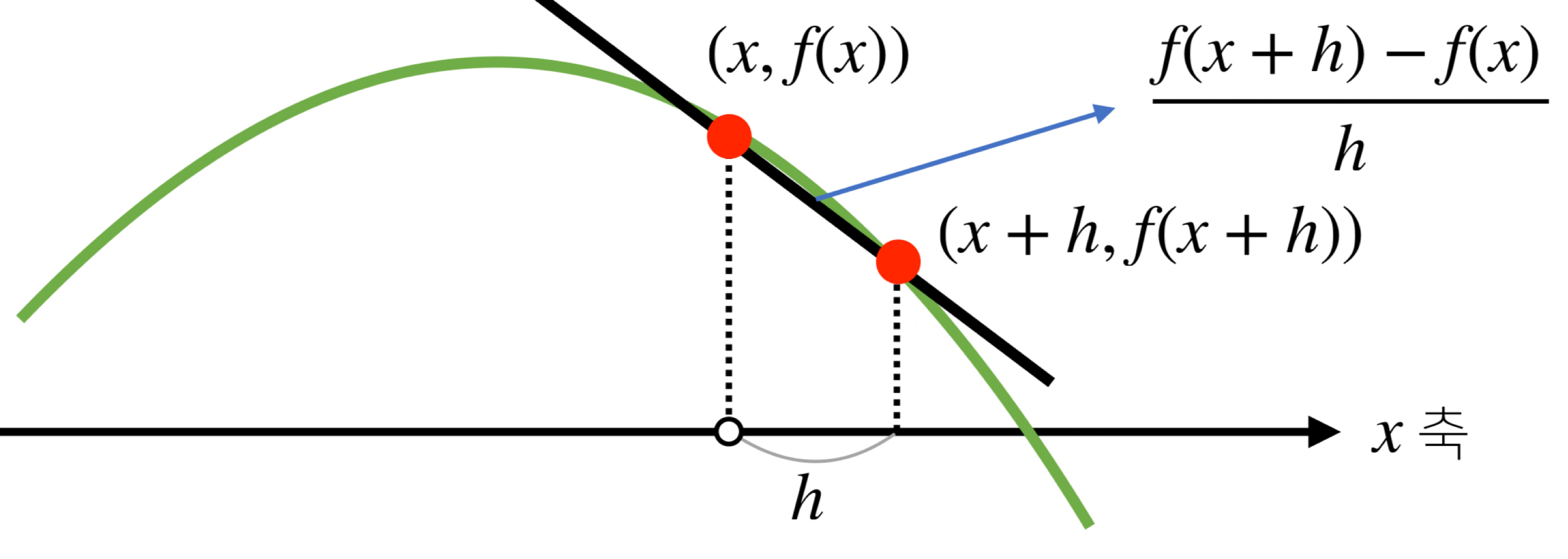
  => 미분값을 더하면 경사상승법(gradient ascent)라고 하며 함수의 극대값의 위치를 구할 때 사용
  => 미분값을 빼면 강사하강법 (gradient descent)이라 하며 함수의 극소값의 위치를 구할 때 사용.

• 종료조건이 성립하기 전까지 미분값을 계속 업데이트함.(극솟값 찾아주기)

• 벡터가 입력인 다변수인 경우 편미분을 사용하고, 각 변수 별로 편미분을 개산한 gradient 벡터를 이용하여 경사하강/경사상승법에 사용할 수 있음.
  

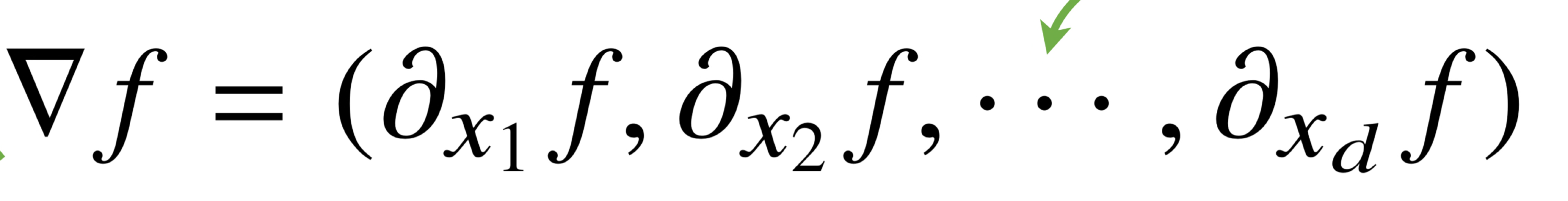
• 선형회귀의 목적식은 $||y-X\beta||_2$이고 이를 최소화하는 $\beta$를 찾아야 하므로 그레디언트 벡터를 구해야함.

  $= -\dfrac{X_1^T(y-X\beta)}{n||y-X\beta||_2},,,, -\dfrac{X_d^T(y-X\beta)}{n||y-X\beta||_2}$

  (복잡한 계산이지만 사실 $X\beta$를 계수 $\beta$에 대해 미분한 결과인 $X^T$만 곱해지는 것)
  => 목적식을 최소화하는 $\beta$를 구하는 경사하강법 알고리즘

  $\beta^(t+1) \leftarrow - \lambda\nabla_\beta||y-X\beta^(t)||$

• 이론적으로 경사하강법은 미분가능하고 볼록한 함수에 대해선 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장되고 있음.
  => But,비선형회귀 문제의 경우 목적식이 볼록하지 않을 수 있으므로 수렴이 항상 보장되지는 않음.
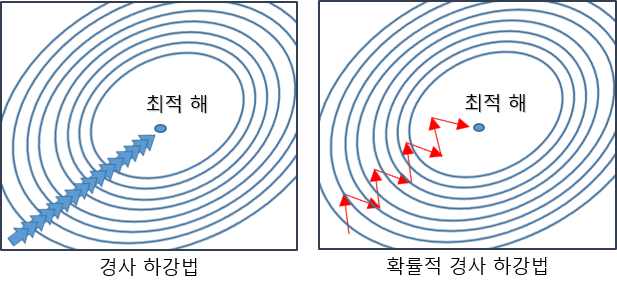
  => 확률적 경사하강법(SGD)를 사용하여 최적화할 수 있음.

• SGD : 데이터 한개 또는 일부를 활용하여 업데이트
  (경사하강법에서는 모든 데이터를 사용해 업데이트)
  

2. 확률론

• 딥러닝은 확률론 기반의 기계학습 이론에 바탕을 두고 있음.
• 히귀 분석에서 손실함수로 사용되는 $L_2$-norm은 예측오차의 분산을 가장 최소화하는 방향으로 학습하도록 유도
• 분류 문제에서 사용되는 cross-entropy는 모델 예측의 불확실성을 최소화하는 방향으로 학습을 유도.
• 확률변수는 확률분포 $D$에 따라 이산형과 연속형 확률변수로 구분됨.
• 이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링함. ($P(X=x)$는 확률변수가 x값을 가질 확률로 해석할 수 있음)
  $P(X\in A) = \sum_{x\in A} P(X=x)$
• 연속형 확률변수는 데이터 공간에 정의된 확률변수의 밀도(density)위에서의 적분을 통해 모델링함.(밀도는 누적확률분포의 변화율을 모델링하며 확률로 해석하면 안됨.)
  $P(X\in A) = \int_A P(x)dx$
• 기대값(expectation,mean)은 데이터를 대표하는 통계량이면서 동시에 확률분포를 통해 다른 통계적 범함수를 계산하는데 사용됨.
  • 연속확률분포의 경우엔 적분을
    $E_{x\sim P(x)}[f(x)] = \int_X f(x)P(x)dx$
  • 이산확률분포의 경우엔 급수를 사용
    $E_{x\sim P(X)}[F(x)\ = \sum_{x \in X}f(x)P(x)$
• 확률분포를 모를때 데이터를 이용하여 기대값을 계산하려면 몬테카를로(Monte Carlo) 샘플링 방법을 사용해야 함.
  • 몬테카를로 샘플링은 독립추출만 보장된다면 대수의 법칙에 의해 수렴성을 보장.
• 최대가능도 추정법(maximum likelihood estimation, MLE)
  - likelihood 함수는 모수 $\widehat{\theta}$를 따르는 분포가 $x$를 관찰할 가능성을 뜻하지만 확률로 해석하면 암됨.
  $\widehat{\theta}_{MLE} = argmaxL(\theta ;x) = argmaxP(x|\theta)$
• 데이터 집합 X가 독립적으로 추출되었을 경우 로그가능도를 촤적화함.
  • 데이터의 숫자가 수억 단위가 된다면 컴푸터의 정확도로는 likelihood를 계산하는 것은 불가능함.
    => 데이터가 독립이리 경우, 로그를 사용하면 likelihood의 곱셈을 로그가능도의 뎃셈으로 바꿀 수 있기 때문에 컴퓨터로 연산이 가능해짐.
  • 경사하강법으로 likelihood를 최적화할 때 미분 연산을 사용하게 되는데, 로그 가능도를 사용하면 연상량을 $O(n^2)$에서 $O(n)$으로 줄여줌(효율적(

3. CNN

4. RNN

---

과제 수행 과정 / 결과물 정리

필수과제 1,2,3은 피드백할 내용이 없음.
(정규표현식을 잘 알아서 코드를 간결하게 짜자)

---

피어세션 정리

21일(수)부터 처음 참여해본 피어세션
다같이 책 읽어보기로 함.
https://d2l.ai/d2l-en.pdf

---

학습 회고

• 수학에서 어려움을 느꼈다. 식을 하나씩 적어가면서 따라가야겠다.
• 이번주는 짧은 시간에 강의를 들었어야해서 급하게 들었지만, 다음주는 차근차근 듣고 정리하는 것이 목표!