Diffusion Model 이해하기 (with DDPM)

들어가며

지금까지 VAE, GAN 등 여러 생성 모델들을 조금씩 알아보았지만, 최근 유명한 생성 모델인 Diffusion Model(확산 모델)은 그만큼 수학적으로 어려운 내용이 많았다. 관련된 논문을 온전히 이해하기 위해 필요한 배경지식도 상당했다. 따라서 이번 글에서는 논문을 처음부터 끝까지 그대로 읽어나가는 대신, 큰 그림부터 차근차근 내가 어려워하는 부분을 중심으로 정리해 보기로 했다.

핵심 아이디어

우선, 확산 모델의 핵심 아이디어는 이렇다.

"우리가 만약 어떤 데이터에 랜덤한 노이즈를 조금씩 조금씩 뿌려서 완전한 노이즈를 만들 수 있다면, 거꾸로 완전한 노이즈에서 처음 데이터를 복원하는 것도 가능하지 않을까?"

처음 들으면 뭔가 시간을 거꾸로 돌려야만 가능할 것 같은 느낌의 발상이지만, 이것이 실제로 가능한 이유는 다음과 같다.

1. 우리에겐 우리가 직접 알기 힘든 현상에 대해 '예측'을 수행할 수 있는 강력한 딥러닝 모델이 있다.
2. 노이즈를 조금 추가하는 것을 '가우시안 분포'로 가정한다면, 충분히 짧은 시간 간격에서 그에 대한 역과정 또한 가우시안 분포로 정의할 수 있다. (#)

특히 2번은 실제 물리학 관점에서의 확산 현상을 자주 예로 들어 설명된다. 물컵에 물감 한 방울을 떨어뜨리면 사방으로 자유분방하게 퍼져나가는 것처럼 보이지만, 아주 짧은 시간 간격 동안 입자 하나하나를 들여다보면 각 입자가 이동할 다음 위치는 항상 가우시안 분포에 의해 결정된다는 것이다.

그래서 확산 모델은 주어진 이미지를 짧은 간격으로 조금씩 노이즈화시키고, 완벽한 노이즈가 완성되면 다시 거꾸로 처음 이미지를 복원하는 방법을 학습한다. 노이즈를 한 번에 원래 이미지로 복원하는 건 어렵겠지만, 현재 이미지에서 '아주 조금 노이즈를 덜어낸' 이미지를 복원하는 일이라면 모델은 충분히 그 방법을 터득할 수 있다.

1. Forward Process

(슬라이드 출처 - CVPR 2022 Tutorial)

확산 모델에서는 노이즈를 추가하는 과정을 'Forward Process' 또는 'Diffusion Process'라고 부른다. 위 그림에서 $\bold{x}_0$이 원래의 이미지이고, 이것이 완전한 노이즈 이미지 $\bold{x}_T$가 될 때까지 매 스텝마다 조금씩 가우시안 노이즈를 추가하는 과정이다.

이때 각 스텝의 이미지 $\bold{x}_t$는 $q(\bold{x}_t|\bold{x}_{t-1})$라는 조건부 확률 분포로부터 나온다고 볼 수 있다. 이 분포는 가우시안 분포로 정의되는데, 그 이유는 당연하지만 주어진 이미지에 가우시안 노이즈를 추가하는 일을 하기 때문이다.

이 가우시안 분포의 평균은 $\sqrt{1-\beta_t}\bold{x_{t-1}}$, 분산은 $\beta_t\bold{I}$으로 정의된다. 여기서 $\beta_t$는 'Variance Schedule'로, 매 스텝 $t$에 따라 조금씩 증가하는 작은 상수이다. (0.0001 ~ 0.02) 그러므로 평균은 이전 스텝 이미지와 비슷하지만 살짝 더 작은 값, 분산은 0보다 살짝 큰 값이 될 것이다. 즉, 이전 이미지보다 모든 픽셀의 평균이 0에 가까워지면서 분산이 조금씩 커진다면 최종적으로는 완전한 가우시안 노이즈 $N(\bold{x_T};\bold{0},\bold{I})$에 도달할 것이라고 짐작할 수 있다.

마르코프 체인

한편, 전체 Forward Process는 조건부 결합 분포(Joint Distribution)인 $q(\bold{x}_{1:T}|\bold{x}_0)=q(\bold{x}_1,\bold{x}_2,...,\bold{x}_T|\bold{x}_0)$으로 요약할 수 있다. 이는 처음에 원본 이미지 $\bold{x}_0$이 주어졌을 때, $\bold{x}_T$까지 모든 이미지에 대한 분포를 차례로 구하는 과정을 떠올리면 이해할 수 있다.

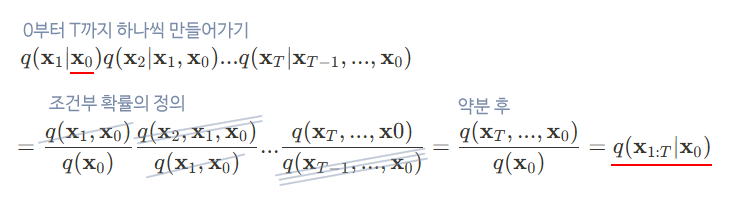
DDPM 논문에서는 '마르코프 체인'의 원리를 적용하여 이 식을 조금 더 직관적인 형태인 $\prod_{t=1}^{T}q(\bold{x}_t|\bold{x}_{t-1})$으로 변형한다.

📌 마르코프 체인(Markov chain)이란?

마르코프 성질을 갖는 이산 시간 확률 과정을 말한다.

• 마르코프 성질: 과거 상태들과 현재 상태가 주어졌을 때, 미래 상태의 조건부 확률 분포가 과거 상태들과는 독립적으로 현재 상태에 의해서만 결정되는 성질.
• 확률 과정: 시간의 진행에 대해 확률적인 변화를 가지는 구조.

즉, $q(\bold{x}_t|\bold{x}_{t-1},\bold{x}_{t-2},...,\bold{x}_0)=q(\bold{x}_t|\bold{x}_{t-1})$로 쓸 수 있게 되므로 $q(\bold{x}_{1:T}|\bold{x}_0)=\prod_{t=1}^{T}q(\bold{x}_t|\bold{x}_{t-1})$이 성립한다.

Reparameterization Trick

Forward Process 자체는 학습되는 과정이 아니다. 정확히는 이 과정에서 만들어지는 $\bold{x}_t$에 대한 분포가 Reverse Process에서 학습의 기준으로 사용되는 것이다.

즉, 굳이 이 단계에서 $T$개의 모든 이미지를 처음부터 하나씩 생성해야 할 필요는 없다. 따라서 우리가 원하는 특정 $t$ 스텝의 이미지 $\bold{x}_t$를 원할 때 한 번에 생성할 수 있도록 수식을 약간 더 개선하면 좋을 것이다.

여기서 'Reparameterization Trick'이라는 기법이 사용된다. 아래 이미지를 보면 이해가 쉬운데, 어떠한 분포 $\mathcal{N}(\mu,\sigma)$를 따르는 $x$가 있다고 할 때, 이 $x$를 $x=\mu+\sigma*\epsilon$ (단, $\epsilon\sim\mathcal{N}(\bold{0},\bold{I})$)와 같은 식으로 표현할 수 있게 해준다. 단순히 원래 분포 표현에서 평균과 표준편차를 밖으로 꺼내고 표준편차에 $\epsilon$을 곱한 후 서로 더해준 형태이다.

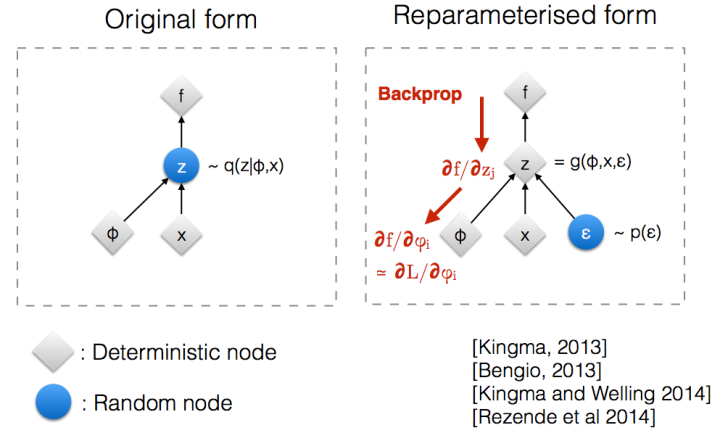
이 기법의 원래 목적은 모델을 학습시킬 때 역전파를 쉽게 흘려주기 위함이다. $q(\bold{x}_t|\bold{x}_0)$은 어쨌든 '확률 분포'이므로, 실제 이미지인 $\bold{x}_t$를 얻으려면 이러한 확률 분포에서 샘플링을 수행해야 하는데, 이것은 완전히 임의적인 행위이므로 '명확한, 결정론적인' 수식을 필요로 하는 역전파를 위해 식을 조금 바꿔주는 것이다. (#1) (#2)

결론적으로 Reparameterization Trick을 이용하면, $q(\bold{x}_t|\bold{x}_0)=\mathcal{N}(\mathbf{x}_{t}; \sqrt{\bar{\alpha_t}}\mathbf{x}_{0},(1-\bar{\alpha}_t) \mathbf{I})$라는 새로운 정의를 얻을 수 있다. (단, $\alpha_t=1-\beta_t$이고 $\bar{\alpha}_{t}=\prod_{s=1}^{t} \alpha_{s}$) 자세한 증명은 아래와 같다.

2. Reverse Process

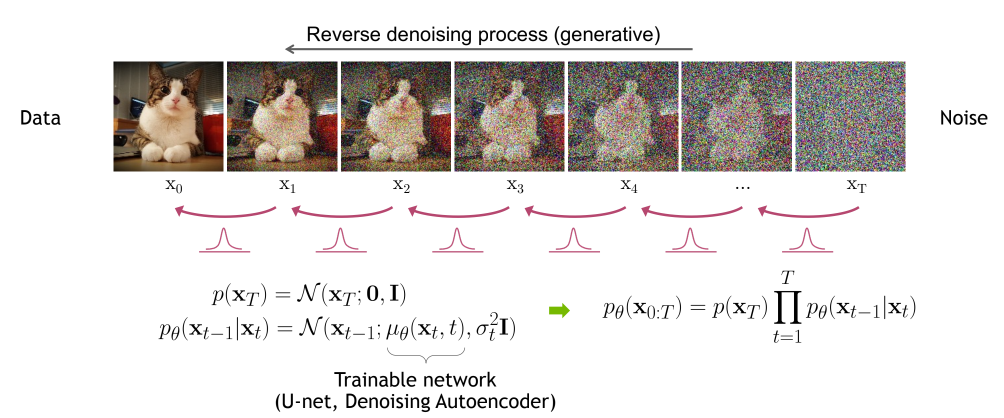
이제는 거꾸로 완전한 가우시안 노이즈로부터 원본 이미지를 복원하는 'Reverse Process'에 대해 알아보자. $t$번째 이미지가 주어졌을 때 $t-1$번째 이미지를 만들어내기 위한 분포는 $p_\theta(\bold{x}_{t-1}|\bold{x}_t)$로 쓸 수 있을 것이고, 전체 과정은 $p_\theta(\bold{x}_{0:T})=p(\bold{x}_T)\prod_{t=1}^{T}p_\theta(\bold{x}_{t-1}|\bold{x}_t)$로 표현할 수 있겠다. (여기서도 마르코프 체인이 사용되었다)

여기서 $p$에 $\theta$가 붙는 이유는 이 분포가 신경망을 통해 학습해야 하는 대상이기 때문이다. 정확히는 우리가 Reverse Process의 분포로 가정한 가우시안 분포의 평균과 표준편차를 학습해야 한다. 일단은 한 번의 스텝에 대한 분포를 $p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t)=\mathcal{N}(\mathbf{x}_{t-1};\mu_\theta(\mathbf{x}_t,t),\sum_\theta(\mathbf{x}_t,t))$로 정의해 두고, 밑에서 Loss를 구할 때 다시 한 번 살펴보도록 하자.

3. Loss Function

신경망이 학습을 진행하려면 먼저 학습의 기준이 되는 Loss Function을 정의해야 한다. 확산 모델의 궁극적인 목적은 다른 생성 모델들과 같이 실제 데이터의 분포를 최대한 잘 추정하는 것, 즉 우리가 추정한 분포인 $p_\theta(\bold{x}_0)$의 가능도를 최대화하는 것이므로, 이에 대한 Negative Log Likelihood를 구해보면 될 것이다.

아래부터는 DDPM 논문에서 소개된 Loss 수식을 처음부터 하나씩 유도해나가는 과정을 정리한 내용이다.

Example of Variational Autoencoder

그 전에, 또 다른 생성 모델인 VAE(Variational Autoencoder)의 Loss를 구하는 과정을 먼저 살펴보자. 이 과정에서 사용되는 많은 기법들이 확산 모델의 Loss를 구할 때에도 사용된다!

주목해서 봐야 할 부분은 이렇다.

1. $\log{p_\theta(x)}$가 모든 잠재 변수 $z$에 대해서 최대가 되길 원하므로, $\log{p_\theta(x)}$에 $z$에 대한 기댓값을 취했다.
2. 베이즈 정리를 이용하여, 직접 구할 수 없는 $p_\theta(x)$를 $z$와 엮어 다른 형태로 변형했다.
3. 분자, 분모에 같은 값을 곱해서 KL Divergence를 형성하게끔 유도했다.

여기서 가장 중요한 부분은, 우리가 직접 계산할 수 없는 분포(여기서는 $p_\theta(z|x)$)를 KL Divergence에 포함시키고, 이것이 항상 0 이상이라는 사실을 이용해 제거하는 것이다. 그러고 나면 남은 식(ELBO)을 최대화하여 근사하는 문제로 바뀌게 된다.

(1) Log Likelihood → Optimizing Variational Bound

다시 확산 모델의 Loss로 돌아와서, $p_\theta(\bold{x}_0)$에 대한 Negative Log Likelihood부터 시작해 보자. VAE의 Loss 식을 유도하는 과정과 거의 비슷한 흐름이다. (#)

(2) Markov Chain → KL Divergence Terms

그 다음, $p_\theta$와 $q$의 결합분포 대신 마르코프 체인을 적용한 버전을 대입하여 차근차근 정리해 보자.

이렇게 확산 모델의 기본적인 Loss 수식이 완성되었다.

이때 중간의 파란색 부분을 보면 마르코프 체인을 사용하여 $q(\bold{x}_t|\bold{x}_{t-1})$를 $q(\bold{x}_t|\bold{x}_{t-1},\bold{x}_0)$으로 바꿔주는 부분이 있다. 이는 최종적으로 해당 항의 $p_\theta$와 $q$ 모두 $(\bold{x}_{t-1}|\bold{x}_t)$에 대한 분포가 되게끔 유도해서 '복원'에 대한 KL Divergence를 구하기 위한 것으로 생각된다. (= 최종 식에서 두 번째 $D_{KL}$항)

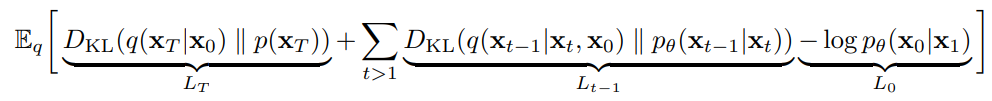
DDPM 논문에서는 위 Loss 식을 이루는 3개의 항을 각각 $L_T$, $L_{t-1}$, $L_0$으로 명명한 후, 추가적인 해석을 덧붙인다. 결론적으로는 여기서 $L_{t-1}$만 구하는 식으로 단순화된다.

• $L_T$: $q(\bold{x}_T|\bold{x}_0)$와 $p(\bold{x}_T)$의 KL Divergence. 즉, Forward Process에서 원본 이미지를 얼마나 가우시안 노이즈와 비슷하게 잘 바꾸냐인데... DDPM에서는 편의상 $\beta_t$를 학습 파라미터가 아닌 상수로 고정하므로 이 항은 최적화와는 무관한 '고정된 과정'이 된다. 즉, 이 항을 통째로 생략해도 무방하다.

• $L_{t-1}$: 모든 t에 대한 $q(\bold{x}_{t-1}|\bold{x}_t)$와 $p_\theta(\bold{x}_{t-1}|\bold{x}_t)$ 간 KL Divergence의 총합. 즉, Reverse Process의 각 스텝에서 이전 스텝의 (노이즈를 살짝 덜어낸) 이미지를 얼마나 잘 복원하는지를 측정한다.

• $L_0$: $\bold{x}_1$에서 $\bold{x}_0$을 복원하는 과정으로, $T$가 보통 2,000 정도 되는 큰 값임을 고려했을 때 이것은 무시해도 될 만큼의 매우 작은 부분이다. (실험적으로도 큰 영향을 주지 않았다고 함) 따라서 이 항도 역시 생략 가능하다.

그렇다면 이제 우리에게 필요한 건 두 번째 KLD 항을 이루는 두 개의 분포 $q(\bold{x}_{t-1}|\bold{x}_t,\bold{x}_0)$과 $p_\theta(\bold{x}_{t-1}|\bold{x}_t)$만 남게 된다. 먼저 $q(\bold{x}_{t-1}|\bold{x}_t,\bold{x}_0)$부터 시작해 보자.

(3) Mean and Variance of $q(\bold{x}_{t-1}|\bold{x}_t,\bold{x}_0)$

아쉽게도 $q(\bold{x}_{t-1}|\bold{x}_t,\bold{x}_0)$의 평균과 분산을 바로 알 수는 없다. 그렇다면 베이즈 정리를 이용해 우리가 이미 알고 있는 분포 $q(\bold{x}_t|\bold{x}_{t-1})$, $q(\bold{x}_t|\bold{x}_0)$, $q(\bold{x}_{t-1}|\bold{x}_0)$에 대한 식으로 변형한 후, 정규 분포 수식에 대입하여 평균과 표준편차를 직접 구해보자.

따라서, 만약 $\displaystyle q(\bold{x}_{t-1}|\bold{x}_t,\bold{x}_0)=\mathcal{N}(\bold{x}_{t-1};\bold{\tilde\mu}_t(\bold{x}_t,\bold{x}_0),\tilde\beta_t\bold{I})$으로 둔다면,

• $\displaystyle \bold{\tilde\mu}_t(\bold{x}_t,\bold{x}_0)=\frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}\bold{x}_t+\frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_t}\bold{x}_0$
• $\displaystyle \tilde\beta_t=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_{t}}\beta_t$

으로 평균과 표준편차를 각각 구할 수 있으며, 여기서 조금 더 나아가 평균을 ($\bold{x}_0$을 제거하고) $\bold{x}_t$에 관한 식으로 한 번 더 정리해 $\bold{\tilde\mu_t}=\frac{1}{\sqrt{\alpha_t}}(\bold{x}_t-\frac{(1-\alpha_t)}{\sqrt{1-\bar\alpha_t}}\epsilon)$으로 만들 수 있다.

(4) Mean and Variance of $p_\theta(\bold{x}_{t-1}|\bold{x}_t)$

다음으로 KLD 항의 두 번째 분포인 $p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t)=\mathcal{N}(\mathbf{x}_{t-1};\mu_\theta(\mathbf{x}_t,t),\sum_\theta(\mathbf{x}_t,t))$에 대해 생각해 보자. Loss를 최소화한다는 것은 결국 해당 KLD 항을 최소화해야 한다는 뜻이고, 따라서 이 분포의 목적은 $q(\bold{x}_{t-1}|\bold{x}_t)$를 최대한 똑같이 근사하는 것이 된다. 즉, 학습 가능한 파라미터를 갖는 신경망을 통해 이 분포의 평균과 표준편차를 학습해야 한다.

다시 위에서 구한 $p_\theta(\bold{x}_{t-1}|\bold{x}_t)$의 평균과 표준편차를 보면, $\alpha_t$와 $\beta_t$는 $t$에 따라 고정되어 있는 상수이고, $\bold{x}_t$는 입력으로 사용되는 이미지이므로, 여기서 학습할 수 있는 인자는 $\epsilon\sim\mathcal{N}(\bold{0},\bold{I})$뿐이다. 따라서 우린 $t$와 $\bold{x}_t$가 입력으로 주어졌을 때 $\epsilon_t$를 예측하는 $\epsilon_\theta(\bold{x}_t,t)$를 이용하여 $p_\theta(\bold{x}_{t-1}|\bold{x}_t)$의 평균을 구할 수 있을 것이다.

• $\displaystyle \mu_\theta(\bold{x}_t,t)=\frac{1}{\sqrt{\alpha_t}}(\bold{x}_t-\frac{(1-\alpha_t)}{\sqrt{1-\bar\alpha_t}}\epsilon_\theta(\bold{x}_t,t))$

또한, DDPM 논문에서는 $p_\theta$의 분산 $\Sigma_{\theta}(\bold{x}_t,t)$를 따로 학습하는 대신, 그냥 상수 $\beta_t$ 또는 $\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}$를 사용한다. 이 말은 곧 $q$의 평균 $\mu_\theta(\bold{x}_t,t)$만 잘 학습하면 된다는 뜻이다.

(5) $L_{t-1}$ and Final Loss

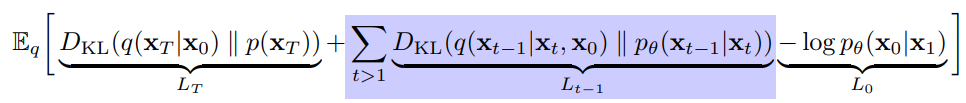
이제 $q(\bold{x}_{t-1}|\bold{x}_t,\bold{x}_0)$과 $p_\theta(\bold{x}_{t-1}|\bold{x}_t)$를 모두 식으로 표현할 수 있게 되었으니, 둘의 KL Divergence를 구해보자.

두 분포 $p$, $q$에 대한 일반적인 KL Divergence 식은 $\displaystyle D_{KL}(p\|q)=∫p(x)\log{\frac{p(x)}{q(x)}}dx$이지만, 만약 $p$, $q$가 모두 가우시안 분포라면 다음과 같이 계산할 수 있음이 증명되어 있다. (#)

• $\displaystyle D_{KL}(p\|q)=\log{\frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}-\frac{1}{2}}$

이때 위에서 말했던 것처럼 DDPM에서 표준편차($\sigma$)는 학습되는 파라미터가 아닌 상수이므로, 최적화를 목적으로 하는 식에서는 제거해도 무방하다. (맨 뒤의 $\frac{1}{2}$ 또한 마찬가지) 그러면 결국 $(\mu_1-\mu_2)^2$만 남는다. 여기에 (3), (4)에서 구한 $q(\bold{x}_{t-1}|\bold{x}_t,\bold{x}_0)$와 $p_\theta(\bold{x}_{t-1}|\bold{x}_t)$의 평균을 각각 대입해 정리해 보자.

이렇게 최종 Loss 수식을 완성했다. 추가로 DDPM 논문에서는 아래와 같이 맨 앞의 상수까지 생략했을 때 성능이 향상되었다고 말한다. 식을 잘 보면 상수나 입력값을 제외하고 오직 $\bold{\epsilon}_\theta(\bold{x}_t, t)$만 파라미터 $\theta$에 의존한다는 것을 알 수 있다.

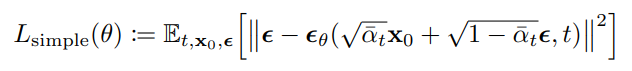
$\bold{\epsilon}_\theta(\bold{x}_t, t)$는 특정 시점 $t$와 그때의 이미지 $\bold{x}_t$가 주어졌을 때, 해당 시점의 노이즈 $\epsilon_t$를 예측하는 네트워크이다. 궁극적으로 DDPM은 '특정 시점의 이미지에 추가된 노이즈'를 최대한 잘 예측하는 것을 목표로 학습하는 모델이라고 결론내릴 수 있다.

요약

마지막으로 Diffusion Model을 간단히 요약하면 아래와 같다.

1. Forward Process는 주어진 데이터에 노이즈를 조금씩 추가하여 완전한 노이즈를 만드는 과정이다.
2. Reverse Process는 완전한 노이즈로부터 거꾸로 조금씩 노이즈를 걷어내는, 즉 원래의 데이터를 복원하는 과정이며, 학습을 위한 신경망이 사용된다.
3. 위 두 가지 과정 모두 매우 짧은 간격 $t$ 스텝을 따라 진행되며, Loss는 특정 $t$ 시점의 데이터에 더해진 노이즈를 예측하는 것을 목적으로 한다.

📖 도움이 된 자료

• Diffusion Presentation (인하대 VCL Lab 조현욱 선배님) - 이번 Diffusion Model의 학습 계기가 된 세미나의 발표 자료입니다. 특히 수식적으로 매우 상세하게 증명 및 정리가 되어있어서 글을 쓸 때 많은 도움이 되었습니다.
• Diffusion Model과 DDPM 수식 유도 과정 (xoft) / Diffusion, DDPM 수식 정복하기 (남웅찬) - DDPM 수식을 이해하고 정리하기 위해 자주 참고했던 글입니다. 마찬가지로 수식에 대한 유도 과정이 잘 설명되어 있습니다.
• Diffusion Model 수학이 포함된 Tutorial / [Paper Review] Denoising Diffusion Probabilistic Models - Diffusion Model과 DDPM의 개략적인 구조와 흐름을 이해하는 데에 많은 도움이 되었던 유튜브 영상입니다.